第十六讲 立体图形的表面积和体积(课件)-2022-2023学年小升初数学专项复习课件(通用版)(共27页)
文档属性
| 名称 | 第十六讲 立体图形的表面积和体积(课件)-2022-2023学年小升初数学专项复习课件(通用版)(共27页) |  | |
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-06 09:55:21 | ||
图片预览







文档简介
立体图形的表面积和体积
小升初专项复习数与代数
知识梳理
01
典例精讲
02
基础训练
03
拓展提升
04
CONTENTS
目录
1
知识梳理
Part One
一、知识梳理
(一)长方体和正方体的表面积
1.定义
长方体或正方体6个面的总面积,叫作它的表面积;
2.长方体的表面积
长方体的表面积=(长×宽+长×高+宽×高)×2
3.正方体的表面积
正方体的表面积=棱长×棱长×6
一、知识梳理
(二)长方体和正方体的体积
1.长方体的体积
长方体的体积=长×宽×高 V=a·b·h
公式变形:长=长方体的体积÷宽÷高 宽=长方体的体积÷长÷高 高=长方体的体积÷长÷宽
长方体的体积=底面积×高 V=Sh
公式变形:高=长方体的体积÷底面积 底面积=长方体的体积÷高
2.正方体的体积
正方体的体积=棱长×棱长×棱长 V=a·a·a=????3
正方体的体积=底面积×高 V=Sh
公式变形:高=正方体的体积÷底面积 底面积=正方体的体积÷高
?
一、知识梳理
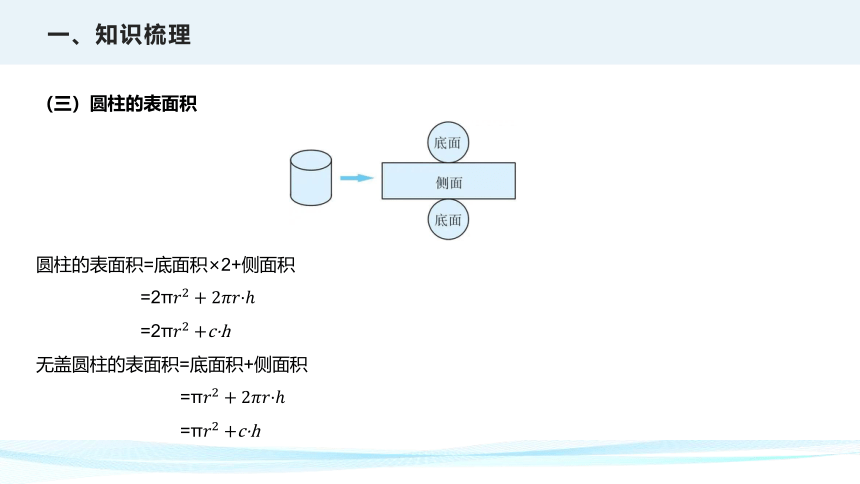
(三)圆柱的表面积
圆柱的表面积=底面积×2+侧面积
=2π????2+2????????·?
=2π????2+c·h
无盖圆柱的表面积=底面积+侧面积
=π????2+2????????·?
=π????2+c·h
?
一、知识梳理
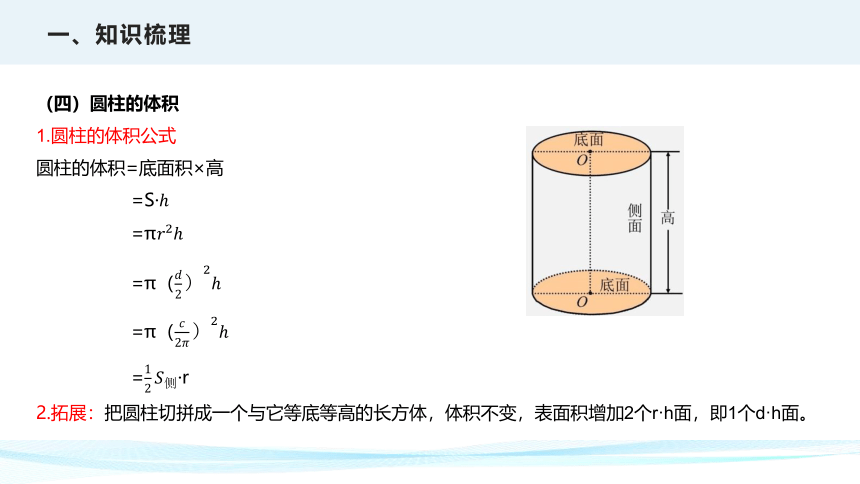
(四)圆柱的体积
1.圆柱的体积公式
圆柱的体积=底面积×高
=S·?
=π????2?
=π(????2)2?
=π(????2????)2?
=12????侧·r
2.拓展:把圆柱切拼成一个与它等底等高的长方体,体积不变,表面积增加2个r·h面,即1个d·h面。
?
一、知识梳理
(五)圆锥的体积
1.圆锥的体积公式
圆锥的体积=13×圆柱的体积
=13S·?
=13π????2?
=13π(????2)2?
2.圆锥的竖切
竖切后的切面是等腰或等边三角形。
竖切后共增加了2个三角形的面积,S切=12dh S增=2S切=dh=2rh
?
一、知识梳理
(六)圆柱和圆锥之间的关系
1.等底等高的圆柱和圆锥
V柱是V锥的3倍。 V锥是V柱的13。
2.等体等高的圆柱和圆锥
S锥是S柱的3倍。 S柱的S锥的13。
3.等体等底的圆柱和圆锥
h锥是h柱的3倍。 h柱的h锥的13。
?
一、知识梳理
(七)求不规则图形的表面积
1. L形立体图形的表面积
把不规则图形用“添补法”变成规则图形,先求出规则图形的表面积,再找出不规则图形的表面积与规则图形的表面积差异之处,最后求出不规则图形的表面积。
2. 领奖台形立体图形的表面积
先算出上下两个立体图形的表面积之和,再减掉重复部分的面积。
一、知识梳理
(八)求不规则图形的体积
1.物体完全浸没在水中,水不溢出
放入物体的体积=现在水的体积-原来水的体积=水上升部分的体积=容积底面积×水面上升的高度
公式变形:
容器底面积=水上升部分的体积÷水面上升的高度
水面上升的高度=水上升部分的体积÷容器底面积
2.物体完全浸没在水中,水溢出
①容器装满水时,放入物体后水溢出。 放入物体的体积=水溢出的体积
②容器没装满水时,放入物体后水溢出。放入物体的体积=上升的水的体积+溢出的水的体积
公式变形:
上升的水的体积=放入物体的体积-溢出的水的体积
溢出的水的体积=放入物体的体积-上升的水的体积
2
典例精讲
Part Two
二、典例精讲
例一:(求抽屉、鱼缸、游泳池、教室粉刷墙面等只有5个面的长方体表面积)
做一个长方体的玻璃鱼缸(无盖),长8分米,宽5分米,高3分米。至少需要多少平方分米的玻璃?
解析:
这个长方体的玻璃鱼缸是无盖的,所以不需要算上面的面积。
3. 8×5+8×3×2+5×3×2=118(平方分米)
答:至少需要118平方分米的玻璃。
二、典例精讲
例二:(求通风管道、柱子、烟囱等只有4个面的长方体表面积)
一种通风管的横截面是边长为0.3米的正方形,每一节通风管的长是3米,如果做10节这样的通风管,需要多少平方米的铁皮?
解析:通风管只有4个面,不需要算前、后两个面。
(0.3×3)×4=3.6(平方米)
3.6×10=36(平方米)
答:需要36平方米的铁皮。
二、典例精讲
例三:如图,从一根高2m的圆柱形木料上截下6dm后,木料的表面积减少了94.2 平方分米。原来木料的表面积是多少平方分米?
解析:底面周长:94.2÷6=15.7(分米)
半径:15.7÷3.14÷2=2.5(分米)
侧面积:2×3.14×2.5×20=314(平方分米)
2个底面积:3.14×2.5×2.5×2=39.25(平方分米)
314+39.25=353.25(平方分米)
答:原来木料的表面积是353.25平方分米。
二、典例精讲
例四:一个底面直径是16厘米,高是8厘米的圆锥形木块,把它分成形状、大小完全相同的两个木块后,表面积比原来增加了多少平方厘米?
解析:把它分成形状、大小完全相同的两个木块后,如图所示
16×8÷2×2
=128÷1
=128(平方厘米)
答:表面积比原来增加了128平方厘米。
3
基础训练
Part Three
三、基础训练
1.一间教室的长8米,宽6.5米,高4米,给这间教室的四周和顶部粉刷墙壁,扣除门窗和黑板的面积22平方米,每平方米需用0.5千克的白灰,粉刷这间教室需要用多少千克的白灰?
4.8×6.5+8×4×2+6.5×4×2=168(平方米)
168-22=146(平方米)
146×0.5=73(千克)
答:粉刷这间教室需要用73千克的白灰。
三、基础训练
2. 一个汽车的油箱是一个长方体,从里面量,长8分米,宽5分米,高3分米,已知汽油每升重0.9千克,这个油箱最多可以装多少千克的汽油?
13.8×5×3=120(升)
120×0.9=108(千克)
答:这个油箱最多可以装108千克的汽油。
三、基础训练
3.圆锥的底面直径为16厘米,高为10厘米,这个圆锥形包装盒的体积是多少立方厘米?(结果保留整数)
13×3.14×8×8×10
=13×2009.6
≈670(立方厘米)
答:这个圆锥形包装盒的体积是670立方厘米。
?
三、基础训练
4.把一个圆柱的侧面沿高展开,得到一个正方形,已知正方形的边长是12.56分米,求圆柱的体积。一个圆锥形物体的底面积是24平方厘米,高是8厘米,这个物体的体积是多少立方厘米?
13×24×8
=8×8
=64 (立方厘米)
答:这个物体的体积是64立方厘米。
?
4
拓展提升
Part Four
四、拓展提升
1.如下图所示(单位:厘米),零件的表面积是多少平方厘米?
添补法,先把不规则图形添补成一个长方体。
长方体的表面积:(4×6+10×6+4×10)×2=248(平方厘米)
长方体的表面积比不规则图形的表面积多了两个长4厘米、宽2厘米的长方形。
248-2×4×2=232(平方厘米)
四、拓展提升
2.如下图所示(单位:厘米),这个立体图形的表面积是多少平方厘米?
先算出上下两个立体图形的表面积之和:
上:2×2×6=24(平方厘米)
下:(5×5+3×5+3×5)×2=110(平方厘米)
上下之和:24+110=134(平方厘米)
重复部分:2×2×2=8(平方厘米)
134-8=126(平方厘米)
四、拓展提升
3.一根铝材可以做一个棱长为6cm的正方体框架,如果将这跟铝材做成一个长8cm,宽5cm的长方体框架,长方体与正方体的体积是否相等?
正方体的棱长之和:6×12=72(cm)
长方体的棱长之和=正方体的棱长之和=72cm。
长方体的高:72÷4-8-5=5(cm)
长方体的体积:5×8×5=200(立方厘米)
正方体的体积:6×6×6=216(立方厘米)
答:长方体和正方体的体积不相等。
四、拓展提升
4.为防控疫情,某工厂紧急生产消毒液,它是圆柱形的,底面直径是5厘米,高12厘米。将24罐这种消毒液装在一个长方体箱内,这个箱子的容积至少是多少立方厘米?
5×6=30(厘米)
5×4=20(厘米)
30×20×12=7200(立方厘米)
答:这个箱子的容积至少是7200立方厘米。
同学们再见!
小升初专项复习数与代数
知识梳理
01
典例精讲
02
基础训练
03
拓展提升
04
CONTENTS
目录
1
知识梳理
Part One
一、知识梳理
(一)长方体和正方体的表面积
1.定义
长方体或正方体6个面的总面积,叫作它的表面积;
2.长方体的表面积
长方体的表面积=(长×宽+长×高+宽×高)×2
3.正方体的表面积
正方体的表面积=棱长×棱长×6
一、知识梳理
(二)长方体和正方体的体积
1.长方体的体积
长方体的体积=长×宽×高 V=a·b·h
公式变形:长=长方体的体积÷宽÷高 宽=长方体的体积÷长÷高 高=长方体的体积÷长÷宽
长方体的体积=底面积×高 V=Sh
公式变形:高=长方体的体积÷底面积 底面积=长方体的体积÷高
2.正方体的体积
正方体的体积=棱长×棱长×棱长 V=a·a·a=????3
正方体的体积=底面积×高 V=Sh
公式变形:高=正方体的体积÷底面积 底面积=正方体的体积÷高
?
一、知识梳理
(三)圆柱的表面积
圆柱的表面积=底面积×2+侧面积
=2π????2+2????????·?
=2π????2+c·h
无盖圆柱的表面积=底面积+侧面积
=π????2+2????????·?
=π????2+c·h
?
一、知识梳理
(四)圆柱的体积
1.圆柱的体积公式
圆柱的体积=底面积×高
=S·?
=π????2?
=π(????2)2?
=π(????2????)2?
=12????侧·r
2.拓展:把圆柱切拼成一个与它等底等高的长方体,体积不变,表面积增加2个r·h面,即1个d·h面。
?
一、知识梳理
(五)圆锥的体积
1.圆锥的体积公式
圆锥的体积=13×圆柱的体积
=13S·?
=13π????2?
=13π(????2)2?
2.圆锥的竖切
竖切后的切面是等腰或等边三角形。
竖切后共增加了2个三角形的面积,S切=12dh S增=2S切=dh=2rh
?
一、知识梳理
(六)圆柱和圆锥之间的关系
1.等底等高的圆柱和圆锥
V柱是V锥的3倍。 V锥是V柱的13。
2.等体等高的圆柱和圆锥
S锥是S柱的3倍。 S柱的S锥的13。
3.等体等底的圆柱和圆锥
h锥是h柱的3倍。 h柱的h锥的13。
?
一、知识梳理
(七)求不规则图形的表面积
1. L形立体图形的表面积
把不规则图形用“添补法”变成规则图形,先求出规则图形的表面积,再找出不规则图形的表面积与规则图形的表面积差异之处,最后求出不规则图形的表面积。
2. 领奖台形立体图形的表面积
先算出上下两个立体图形的表面积之和,再减掉重复部分的面积。
一、知识梳理
(八)求不规则图形的体积
1.物体完全浸没在水中,水不溢出
放入物体的体积=现在水的体积-原来水的体积=水上升部分的体积=容积底面积×水面上升的高度
公式变形:
容器底面积=水上升部分的体积÷水面上升的高度
水面上升的高度=水上升部分的体积÷容器底面积
2.物体完全浸没在水中,水溢出
①容器装满水时,放入物体后水溢出。 放入物体的体积=水溢出的体积
②容器没装满水时,放入物体后水溢出。放入物体的体积=上升的水的体积+溢出的水的体积
公式变形:
上升的水的体积=放入物体的体积-溢出的水的体积
溢出的水的体积=放入物体的体积-上升的水的体积
2
典例精讲
Part Two
二、典例精讲
例一:(求抽屉、鱼缸、游泳池、教室粉刷墙面等只有5个面的长方体表面积)
做一个长方体的玻璃鱼缸(无盖),长8分米,宽5分米,高3分米。至少需要多少平方分米的玻璃?
解析:
这个长方体的玻璃鱼缸是无盖的,所以不需要算上面的面积。
3. 8×5+8×3×2+5×3×2=118(平方分米)
答:至少需要118平方分米的玻璃。
二、典例精讲
例二:(求通风管道、柱子、烟囱等只有4个面的长方体表面积)
一种通风管的横截面是边长为0.3米的正方形,每一节通风管的长是3米,如果做10节这样的通风管,需要多少平方米的铁皮?
解析:通风管只有4个面,不需要算前、后两个面。
(0.3×3)×4=3.6(平方米)
3.6×10=36(平方米)
答:需要36平方米的铁皮。
二、典例精讲
例三:如图,从一根高2m的圆柱形木料上截下6dm后,木料的表面积减少了94.2 平方分米。原来木料的表面积是多少平方分米?
解析:底面周长:94.2÷6=15.7(分米)
半径:15.7÷3.14÷2=2.5(分米)
侧面积:2×3.14×2.5×20=314(平方分米)
2个底面积:3.14×2.5×2.5×2=39.25(平方分米)
314+39.25=353.25(平方分米)
答:原来木料的表面积是353.25平方分米。
二、典例精讲
例四:一个底面直径是16厘米,高是8厘米的圆锥形木块,把它分成形状、大小完全相同的两个木块后,表面积比原来增加了多少平方厘米?
解析:把它分成形状、大小完全相同的两个木块后,如图所示
16×8÷2×2
=128÷1
=128(平方厘米)
答:表面积比原来增加了128平方厘米。
3
基础训练
Part Three
三、基础训练
1.一间教室的长8米,宽6.5米,高4米,给这间教室的四周和顶部粉刷墙壁,扣除门窗和黑板的面积22平方米,每平方米需用0.5千克的白灰,粉刷这间教室需要用多少千克的白灰?
4.8×6.5+8×4×2+6.5×4×2=168(平方米)
168-22=146(平方米)
146×0.5=73(千克)
答:粉刷这间教室需要用73千克的白灰。
三、基础训练
2. 一个汽车的油箱是一个长方体,从里面量,长8分米,宽5分米,高3分米,已知汽油每升重0.9千克,这个油箱最多可以装多少千克的汽油?
13.8×5×3=120(升)
120×0.9=108(千克)
答:这个油箱最多可以装108千克的汽油。
三、基础训练
3.圆锥的底面直径为16厘米,高为10厘米,这个圆锥形包装盒的体积是多少立方厘米?(结果保留整数)
13×3.14×8×8×10
=13×2009.6
≈670(立方厘米)
答:这个圆锥形包装盒的体积是670立方厘米。
?
三、基础训练
4.把一个圆柱的侧面沿高展开,得到一个正方形,已知正方形的边长是12.56分米,求圆柱的体积。一个圆锥形物体的底面积是24平方厘米,高是8厘米,这个物体的体积是多少立方厘米?
13×24×8
=8×8
=64 (立方厘米)
答:这个物体的体积是64立方厘米。
?
4
拓展提升
Part Four
四、拓展提升
1.如下图所示(单位:厘米),零件的表面积是多少平方厘米?
添补法,先把不规则图形添补成一个长方体。
长方体的表面积:(4×6+10×6+4×10)×2=248(平方厘米)
长方体的表面积比不规则图形的表面积多了两个长4厘米、宽2厘米的长方形。
248-2×4×2=232(平方厘米)
四、拓展提升
2.如下图所示(单位:厘米),这个立体图形的表面积是多少平方厘米?
先算出上下两个立体图形的表面积之和:
上:2×2×6=24(平方厘米)
下:(5×5+3×5+3×5)×2=110(平方厘米)
上下之和:24+110=134(平方厘米)
重复部分:2×2×2=8(平方厘米)
134-8=126(平方厘米)
四、拓展提升
3.一根铝材可以做一个棱长为6cm的正方体框架,如果将这跟铝材做成一个长8cm,宽5cm的长方体框架,长方体与正方体的体积是否相等?
正方体的棱长之和:6×12=72(cm)
长方体的棱长之和=正方体的棱长之和=72cm。
长方体的高:72÷4-8-5=5(cm)
长方体的体积:5×8×5=200(立方厘米)
正方体的体积:6×6×6=216(立方厘米)
答:长方体和正方体的体积不相等。
四、拓展提升
4.为防控疫情,某工厂紧急生产消毒液,它是圆柱形的,底面直径是5厘米,高12厘米。将24罐这种消毒液装在一个长方体箱内,这个箱子的容积至少是多少立方厘米?
5×6=30(厘米)
5×4=20(厘米)
30×20×12=7200(立方厘米)
答:这个箱子的容积至少是7200立方厘米。
同学们再见!
同课章节目录
