第十四讲 平面图形的周长和面积(课件)-2022-2023学年小升初数学专项复习课件(通用版)(共26张PPT))
文档属性
| 名称 | 第十四讲 平面图形的周长和面积(课件)-2022-2023学年小升初数学专项复习课件(通用版)(共26张PPT)) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-06 00:00:00 | ||
图片预览







文档简介
平面图形的周长和面积
小升初专项复习数与代数
知识梳理
01
典例精讲
02
基础训练
03
拓展提升
04
CONTENTS
目录
1
知识梳理
Part One
一、知识梳理
(一)周长和面积
1.周长定义
封闭图形一周的长度,是它的周长。
2.面积定义
物体的表面或封闭图形的大小,就是它们的面积。
3.周长和面积的区别
①周长是指封闭图形一周的长度,而面积是指物体所占平面的大小。
②单位不同:周长是长度单位,面积是面积单位。
一、知识梳理
(二)长方形、正方形的周长和面积公式
1.周长公式
长方形的周长=(长+宽)×2
公式变形:长=长方形的周长÷2-宽
宽=长方形的周长÷2-长
正方形的周长=边长×4
公式变形:边长=正方形的周长÷4
2.面积公式
长方形的面积=长×宽
公式变形:长=长方形的面积÷宽
宽=长方形的面积÷长
正方形的面积=边长×边长
一、知识梳理
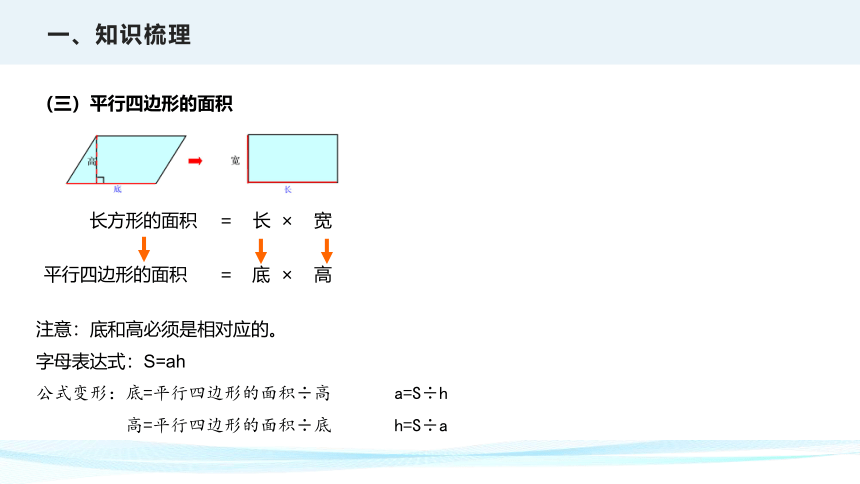
(三)平行四边形的面积
注意:底和高必须是相对应的。
字母表达式:S=ah
公式变形:底=平行四边形的面积÷高 a=S÷h
高=平行四边形的面积÷底 h=S÷a
= ×
长方形的面积
平行四边形的面积
长
底
宽
高
= ×
一、知识梳理
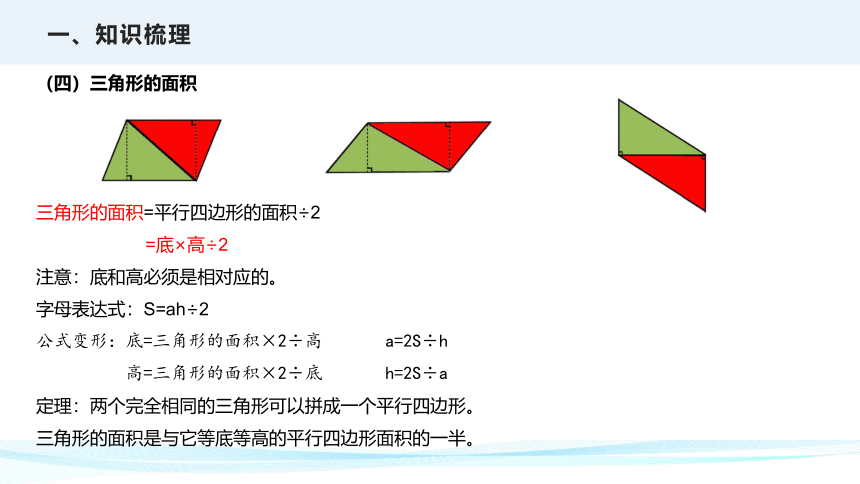
(四)三角形的面积
三角形的面积=平行四边形的面积÷2
=底×高÷2
注意:底和高必须是相对应的。
字母表达式:S=ah÷2
公式变形:底=三角形的面积×2÷高 a=2S÷h
高=三角形的面积×2÷底 h=2S÷a
定理:两个完全相同的三角形可以拼成一个平行四边形。
三角形的面积是与它等底等高的平行四边形面积的一半。
一、知识梳理
(五)梯形的面积
梯形的面积=平行四边形的面积÷2
=(上底+下底)×高÷2
字母表达式:S=(a+b)h÷2
公式变形:上底+下底=梯形的面积×2÷高 a+b=2S÷h
高=梯形的面积×2÷(上底+下底) h=2S÷(a+b)
定理:两个完全相同的梯形可以拼成一个平行四边形。
一、知识梳理
(六)组合图形的面积
1.割补法
把一个图形的某一部分割下来,填补在图形的某一部分,在原来面积不变的情况下,使其转化成已经掌握的旧的图形,以利于公式的推导。
2.分割法
把一个不规则图形分割成几个规则图形,分别求出这些规则图形的面积,再把面积相加就是不规则图形的面积。
3.添补法
把一个不规则图形添上一块规则图形,使其转化成已经掌握的旧的图形,先算出旧的图形的面积,再算出补上的图形的面积,再相减就是不规则图形的面积。
一、知识梳理
(七)圆的周长和面积
1.圆的周长
已知半径,求周长:C=2πr
已知直径,求周长:C=πd
已知周长,求半径:r=C÷π÷2
已知周长,求直径:d=C÷π
2.圆的面积
已知半径,求面积:S=π????2
已知直径,求面积:S=π(????2)2
已知周长,求面积:S=π(C÷π÷2)2
?
一、知识梳理
(八)圆环的面积
圆环的面积=????大圆-????小圆
=π????2-π????2
=π(????2?????2)
?
2
典例精讲
Part Two
二、典例精讲
例一:火眼金睛辨对错
1.圆的周长总是直径的3.14倍。( )
解析:圆的周长是直径的π倍。
2.把一个长方形的木框拉成一个平行四边形,周长和面积都不变。( )
解析:把一个长方形的木框拉成一个平行四边形,周长不变,面积减小。
3.两个梯形一定能拼成一个平行四边形。( )
解析:两个完全相同的梯形一定能拼成一个平行四边形。
×
×
×
二、典例精讲
例二:选择题
2.下列说法正确的是( )。
A.面积相等的两个三角形一定等底等高
B.两个面积相等的三角形一定可以拼成一个平行四边形
C.每个三角形都有三条高
解析:面积相等的两个三角形不一定等底等高。
两个完全相同的三角形一定可以拼成一个平行四边形。
C
二、典例精讲
例三:计算下面图形的周长和面积。(单位:厘米)
解析:半径=10÷2=5(厘米)
圆的周长=πd=21.4(厘米)
半圆的周长=31.4÷2+10=25.7(厘米)
圆的面积=π????2=3.14×5×5=78.5(平方厘米)
半圆的面积=78.5÷2=39.25(平方厘米)
答:周长是25.7厘米,面积是39.25平方厘米。
?
二、典例精讲
例四:已知图中正方形的面积是20平方厘米,这个圆的面积是多少平方厘米?
解析:正方形的面积=边长×边长=20(平方厘米)
圆的半径=正方形的边长
所以半径×半径=20
所以圆的面积=3.14×20=62.8(平方厘米)
3
基础训练
Part Three
三、基础训练
1.选择题
①一个三角形的底是10厘米,面积是50平方厘米,它的高是( )厘米。
A.5 B.10 C.2.5
②一个直角三角形的三条边分别是3厘米、4厘米、5厘米,这个三角形的面积是( ) 平方厘米。
A.6 B.10 C.7.5
③三角形和平行四边形的底相等,面积也相等,已知三角形的高是12厘米,平行四边形的高是( ) 厘米。
A.12 B.24 C.6
B
A
C
三、基础训练
2.如右图,平行四边形的面积是40平方厘米,求出其他两个图形的面积。(单位:厘米)
40÷5=8(厘米)
长方形的面积:6×8=48(平方厘米)
圆形的面积:3.14×(8÷2)×(8÷2)=50.24(平方厘米)
三、基础训练
3.一个梯形苹果园,上底长16米,下底长38米,高是30米。如果每棵苹果树占地9平方米,这个果园一共可以栽苹果树多少棵?
(16+38)×30÷2
=54×30÷2
=810(平方米)
810÷9=90(棵)
答:这个果园一共可以栽苹果树90棵。
三、基础训练
4.计算下图阴影部分的面积。(单位:厘米)
圆的面积:3.14×2×2=12.56(平方厘米)
半圆的面积:12.56÷2=6.28(平方厘米)
三角形的面积:4×2÷2=4(平方厘米)
梯形的面积:(4+6)×2÷2=10(平方厘米)
阴影部分的面积:6.28-4+10-6.28=6(平方厘米)
4
拓展提升
Part Four
四、拓展提升
1.如图半圆中,AB为直径, C为弧AB的中点,求阴影部分的面积之和。(π取3.14)(单位:厘米)
r=(6+6+3+3)÷2=9(厘米)
阴影部分的面积=圆的面积÷4
=3.14×9×9÷4
=63.585(平方厘米)
答:阴影部分的面积是63.585平方厘米。
四、拓展提升
2.小敏用7cm长的半径画了三个圆,并且每个圆都过另外两个圆的圆心(如图所示)。她想求出图中阴影部分面积的和,你能帮她解决吗?(圆周率π取227)
227×7×7×3×60360
=462×16
=77(平方厘米)
?
四、拓展提升
3.如下图,阴影部分的面积为多少平方厘米?(π取3.14)
先算左下角空白的面积=长方形的面积-小扇形的面积
=10×6-3.14×6×6÷4
=60-28.26
=31.74(平方厘米)
阴影部分的面积=大扇形的面积-左边空白的面积
=3.14×10×10÷4-31.74
=46.76(平方厘米)
答:阴影部分的面积为46.76平方厘米。
同学们再见!
小升初专项复习数与代数
知识梳理
01
典例精讲
02
基础训练
03
拓展提升
04
CONTENTS
目录
1
知识梳理
Part One
一、知识梳理
(一)周长和面积
1.周长定义
封闭图形一周的长度,是它的周长。
2.面积定义
物体的表面或封闭图形的大小,就是它们的面积。
3.周长和面积的区别
①周长是指封闭图形一周的长度,而面积是指物体所占平面的大小。
②单位不同:周长是长度单位,面积是面积单位。
一、知识梳理
(二)长方形、正方形的周长和面积公式
1.周长公式
长方形的周长=(长+宽)×2
公式变形:长=长方形的周长÷2-宽
宽=长方形的周长÷2-长
正方形的周长=边长×4
公式变形:边长=正方形的周长÷4
2.面积公式
长方形的面积=长×宽
公式变形:长=长方形的面积÷宽
宽=长方形的面积÷长
正方形的面积=边长×边长
一、知识梳理
(三)平行四边形的面积
注意:底和高必须是相对应的。
字母表达式:S=ah
公式变形:底=平行四边形的面积÷高 a=S÷h
高=平行四边形的面积÷底 h=S÷a
= ×
长方形的面积
平行四边形的面积
长
底
宽
高
= ×
一、知识梳理
(四)三角形的面积
三角形的面积=平行四边形的面积÷2
=底×高÷2
注意:底和高必须是相对应的。
字母表达式:S=ah÷2
公式变形:底=三角形的面积×2÷高 a=2S÷h
高=三角形的面积×2÷底 h=2S÷a
定理:两个完全相同的三角形可以拼成一个平行四边形。
三角形的面积是与它等底等高的平行四边形面积的一半。
一、知识梳理
(五)梯形的面积
梯形的面积=平行四边形的面积÷2
=(上底+下底)×高÷2
字母表达式:S=(a+b)h÷2
公式变形:上底+下底=梯形的面积×2÷高 a+b=2S÷h
高=梯形的面积×2÷(上底+下底) h=2S÷(a+b)
定理:两个完全相同的梯形可以拼成一个平行四边形。
一、知识梳理
(六)组合图形的面积
1.割补法
把一个图形的某一部分割下来,填补在图形的某一部分,在原来面积不变的情况下,使其转化成已经掌握的旧的图形,以利于公式的推导。
2.分割法
把一个不规则图形分割成几个规则图形,分别求出这些规则图形的面积,再把面积相加就是不规则图形的面积。
3.添补法
把一个不规则图形添上一块规则图形,使其转化成已经掌握的旧的图形,先算出旧的图形的面积,再算出补上的图形的面积,再相减就是不规则图形的面积。
一、知识梳理
(七)圆的周长和面积
1.圆的周长
已知半径,求周长:C=2πr
已知直径,求周长:C=πd
已知周长,求半径:r=C÷π÷2
已知周长,求直径:d=C÷π
2.圆的面积
已知半径,求面积:S=π????2
已知直径,求面积:S=π(????2)2
已知周长,求面积:S=π(C÷π÷2)2
?
一、知识梳理
(八)圆环的面积
圆环的面积=????大圆-????小圆
=π????2-π????2
=π(????2?????2)
?
2
典例精讲
Part Two
二、典例精讲
例一:火眼金睛辨对错
1.圆的周长总是直径的3.14倍。( )
解析:圆的周长是直径的π倍。
2.把一个长方形的木框拉成一个平行四边形,周长和面积都不变。( )
解析:把一个长方形的木框拉成一个平行四边形,周长不变,面积减小。
3.两个梯形一定能拼成一个平行四边形。( )
解析:两个完全相同的梯形一定能拼成一个平行四边形。
×
×
×
二、典例精讲
例二:选择题
2.下列说法正确的是( )。
A.面积相等的两个三角形一定等底等高
B.两个面积相等的三角形一定可以拼成一个平行四边形
C.每个三角形都有三条高
解析:面积相等的两个三角形不一定等底等高。
两个完全相同的三角形一定可以拼成一个平行四边形。
C
二、典例精讲
例三:计算下面图形的周长和面积。(单位:厘米)
解析:半径=10÷2=5(厘米)
圆的周长=πd=21.4(厘米)
半圆的周长=31.4÷2+10=25.7(厘米)
圆的面积=π????2=3.14×5×5=78.5(平方厘米)
半圆的面积=78.5÷2=39.25(平方厘米)
答:周长是25.7厘米,面积是39.25平方厘米。
?
二、典例精讲
例四:已知图中正方形的面积是20平方厘米,这个圆的面积是多少平方厘米?
解析:正方形的面积=边长×边长=20(平方厘米)
圆的半径=正方形的边长
所以半径×半径=20
所以圆的面积=3.14×20=62.8(平方厘米)
3
基础训练
Part Three
三、基础训练
1.选择题
①一个三角形的底是10厘米,面积是50平方厘米,它的高是( )厘米。
A.5 B.10 C.2.5
②一个直角三角形的三条边分别是3厘米、4厘米、5厘米,这个三角形的面积是( ) 平方厘米。
A.6 B.10 C.7.5
③三角形和平行四边形的底相等,面积也相等,已知三角形的高是12厘米,平行四边形的高是( ) 厘米。
A.12 B.24 C.6
B
A
C
三、基础训练
2.如右图,平行四边形的面积是40平方厘米,求出其他两个图形的面积。(单位:厘米)
40÷5=8(厘米)
长方形的面积:6×8=48(平方厘米)
圆形的面积:3.14×(8÷2)×(8÷2)=50.24(平方厘米)
三、基础训练
3.一个梯形苹果园,上底长16米,下底长38米,高是30米。如果每棵苹果树占地9平方米,这个果园一共可以栽苹果树多少棵?
(16+38)×30÷2
=54×30÷2
=810(平方米)
810÷9=90(棵)
答:这个果园一共可以栽苹果树90棵。
三、基础训练
4.计算下图阴影部分的面积。(单位:厘米)
圆的面积:3.14×2×2=12.56(平方厘米)
半圆的面积:12.56÷2=6.28(平方厘米)
三角形的面积:4×2÷2=4(平方厘米)
梯形的面积:(4+6)×2÷2=10(平方厘米)
阴影部分的面积:6.28-4+10-6.28=6(平方厘米)
4
拓展提升
Part Four
四、拓展提升
1.如图半圆中,AB为直径, C为弧AB的中点,求阴影部分的面积之和。(π取3.14)(单位:厘米)
r=(6+6+3+3)÷2=9(厘米)
阴影部分的面积=圆的面积÷4
=3.14×9×9÷4
=63.585(平方厘米)
答:阴影部分的面积是63.585平方厘米。
四、拓展提升
2.小敏用7cm长的半径画了三个圆,并且每个圆都过另外两个圆的圆心(如图所示)。她想求出图中阴影部分面积的和,你能帮她解决吗?(圆周率π取227)
227×7×7×3×60360
=462×16
=77(平方厘米)
?
四、拓展提升
3.如下图,阴影部分的面积为多少平方厘米?(π取3.14)
先算左下角空白的面积=长方形的面积-小扇形的面积
=10×6-3.14×6×6÷4
=60-28.26
=31.74(平方厘米)
阴影部分的面积=大扇形的面积-左边空白的面积
=3.14×10×10÷4-31.74
=46.76(平方厘米)
答:阴影部分的面积为46.76平方厘米。
同学们再见!
同课章节目录
