2022-2023学年人教B版(2019)必修二 第六章 平面向量初步 单元测试卷(含解析)
文档属性
| 名称 | 2022-2023学年人教B版(2019)必修二 第六章 平面向量初步 单元测试卷(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 510.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-05 00:00:00 | ||
图片预览



文档简介
人教B版(2019)必修二 第六章 平面向量初步 单元测试卷
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1、在边长为2的正方形ABCD中,E为CD的中点,AE交BD于点F.若,则( )
A.1 B. C. D.
2、在中,,则( )
A. B. C. D.
3、已知O,N,P在所在平面内,满足,,且,则点O,N,P依次是的( )
A.重心,外心,垂心 B.重心,外心,内心
C.外心,重心,垂心 D.外心,重心,内心
4、用两条成120°角的等长的绳子悬挂一个灯具,已知灯具重10N,则每根绳子的拉力大小为( )N
A.10 B.5 C. D.
5、设点O是正三角形ABC的中心,则向量,,是( ).
A.相同的向量 B.模相等的向量 C.共线向量 D.共起点的向量
6、已知平面向量,,若存在实数,使得,则实数m的值为( ).
A.-4 B.12 C.-1 D.1
7、已知,,点P是线段MN上的点,且,则P点的坐标为( )
A. B. C. D.
8、若AD是的中线,已知,,则等于( )
A. B. C. D.
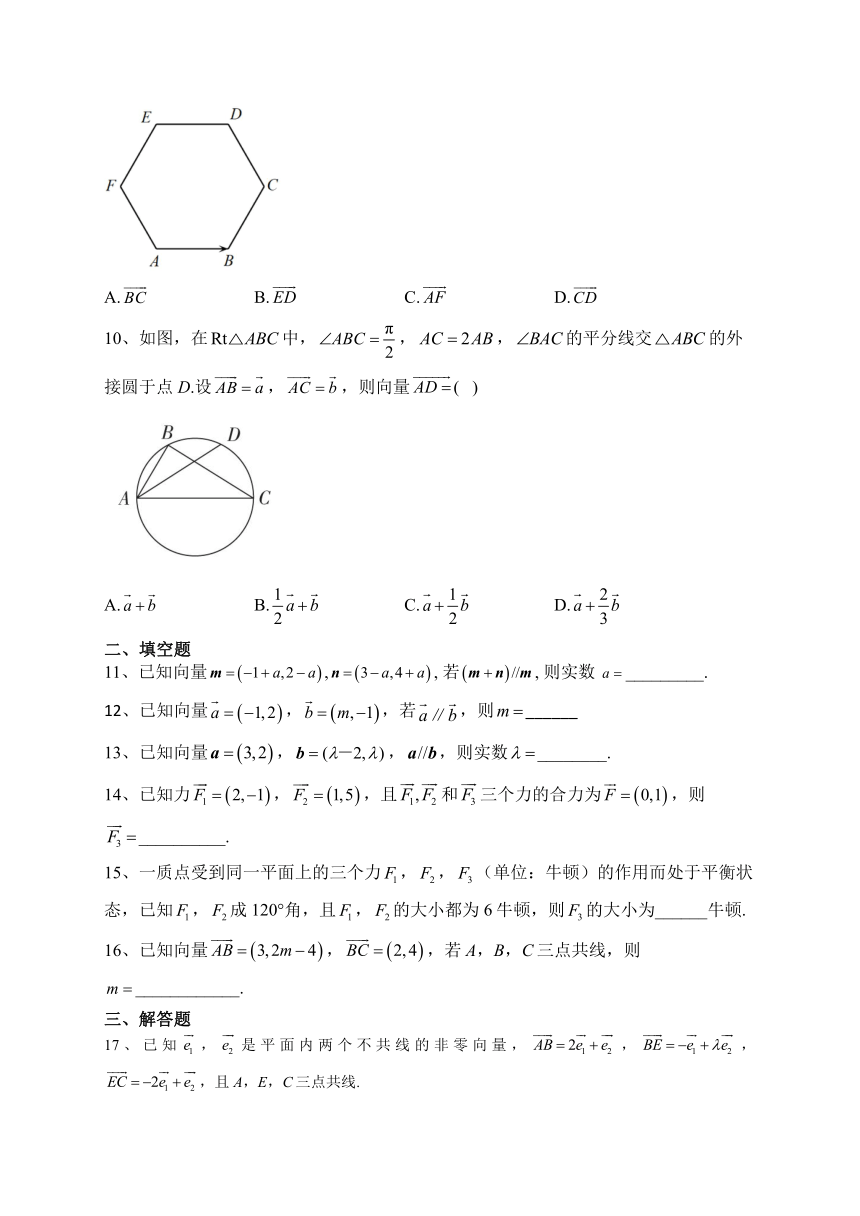
9、如图,在正六边形ABCDEF中,与向量相等的向量是( )
A. B. C. D.
10、如图,在中,,,的平分线交的外接圆于点D.设,,则向量( )
A. B. C. D.
二、填空题
11、已知向量,, 若, 则实数 _________.
12、已知向量,,若,则______
13、已知向量,,,则实数________.
14、已知力,,且和三个力的合力为,则__________.
15、一质点受到同一平面上的三个力,,(单位:牛顿)的作用而处于平衡状态,已知,成120°角,且,的大小都为6牛顿,则的大小为______牛顿.
16、已知向量,,若A,B,C三点共线,则____________.
三、解答题
17、已知,是平面内两个不共线的非零向量,,,,且A,E,C三点共线.
(1)求实数的值;
(2)若,,求的坐标;
(3)已知,在(2)的条件下,若A,B,C,D四点按逆时针顺序构成平行四边形,求点A的坐标.
18、如图所示,在中,.
(1)用表示;
(2)M为内一点,且,证明:B,M,E三点共线.
19、已知直线,点是直线l上的两点.
(1)若为零向量,求x,y的值;
(2)若为单位向量,求x,y的值.
20、已知.设,且.
(1)求;
(2)求满足的实数m,n;
(3)求点M,N的坐标及的坐标.
参考答案
1、答案:B
解析:根据题意得,,所以,所以,所以.又因为,所以即所以,故选B.
2、答案:B
解析:如图,过点D分别作AC,AB的平行线,交AB,AC于E,F,则四边形AEDF为平行四边形,
所以,因为,所以,
,所以.故选B.
3、答案:C
解析:由知点O到A,B,C三点的距离相等,所以O为的外心.由,知.设AB的中点为D,则,
所以点N在的中线AD上且,所以N为的重心.由,得,即,所以,
同理可得,,所以P为的垂心.故选C.
4、答案:A
解析:如图所示,可得,,且,
所以,为等边三角形,
所以,即每根绳子的拉力大小为10N.
故选:A.
5、答案:B
解析:O是正的中心,
向量,,分别是以三角形的中心和顶点为起点和终点的,
O是正三角形的中心,
O到三个顶点的距离相等,
即,
故选:B.
6、答案:D
解析:由得,,或,
,,从而.
故选:D.
7、答案:A
解析:设,则,,因,
从而有,解得,
所以P点的坐标为.
故选:A.
8、答案:D
解析:因为D是BC的中点,由向量的平行四边形法则可得:,
故选:D.
9、答案:B
解析:由图可知六边形ABCDEF是正六边形,所以,与方向相同的只有;而,,与长度相等,方向不同,所以选项A,C,D,均错误;
故选:B
10、答案:C
解析:由题意知,AC为的外接圆的直径.
设△ABC的外接圆圆心为O,如图,连接OD,BD,则.
所以,
因为,
所以,
所以,
因为.
所以四边形ABDO是平行四边形,
所以,
故选:C.
11、答案:
解析:, 由, 得, 解得.
12、答案:
解析:因为向量,,且,
所以,解得.
故答案为:.
13、答案:
解析:因为,所以,所以.
14、答案:
解析:设,则,即,解得,
所以.
故答案为:.
15、答案:6
解析:设三个力,,分别对于的向量为:,,,
则由题知,
所以,
所以,
又,,,
所以,
所以的大小为:6.
故答案为:6.
16、答案:5
解析:由A,B,C三点共线知,则,解得.
故答案为:5.
17、
(1)答案:
解析:.
因为A,E,C三点共线,所以存在实数k,使得,
即,得.
因为,是平面内两个不共线的非零向量,所以,解得,.
(2)答案:
解析:.
(3)答案:
解析:因为A,B,C,D四点按逆时针顺序构成平行四边形,所以.
设,则,
因为,所以解得,即点A的坐标为.
18、答案:(1);
(2)见解析
解析:(1)因为,所以,
所以.
因为,所以,所以.
(2)因为,所以.
因为,所以,即与共线.
因为与有公共点B,所以B,M,E三点共线.
19、答案:(1)
(2)或
解析:(1)当为零向量时,点B与点A重合,此时.
(2)当为单位向量时,,即点A与点B之间的距离为1,
所以,即,
将代入,化简得,
所以或.
20、答案:(1)
(2)
(3);;
解析:(1)由已知得.
.
(2),
解得
(3),
.
又,
.
.
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1、在边长为2的正方形ABCD中,E为CD的中点,AE交BD于点F.若,则( )
A.1 B. C. D.
2、在中,,则( )
A. B. C. D.
3、已知O,N,P在所在平面内,满足,,且,则点O,N,P依次是的( )
A.重心,外心,垂心 B.重心,外心,内心
C.外心,重心,垂心 D.外心,重心,内心
4、用两条成120°角的等长的绳子悬挂一个灯具,已知灯具重10N,则每根绳子的拉力大小为( )N
A.10 B.5 C. D.
5、设点O是正三角形ABC的中心,则向量,,是( ).
A.相同的向量 B.模相等的向量 C.共线向量 D.共起点的向量
6、已知平面向量,,若存在实数,使得,则实数m的值为( ).
A.-4 B.12 C.-1 D.1
7、已知,,点P是线段MN上的点,且,则P点的坐标为( )
A. B. C. D.
8、若AD是的中线,已知,,则等于( )
A. B. C. D.
9、如图,在正六边形ABCDEF中,与向量相等的向量是( )
A. B. C. D.
10、如图,在中,,,的平分线交的外接圆于点D.设,,则向量( )
A. B. C. D.
二、填空题
11、已知向量,, 若, 则实数 _________.
12、已知向量,,若,则______
13、已知向量,,,则实数________.
14、已知力,,且和三个力的合力为,则__________.
15、一质点受到同一平面上的三个力,,(单位:牛顿)的作用而处于平衡状态,已知,成120°角,且,的大小都为6牛顿,则的大小为______牛顿.
16、已知向量,,若A,B,C三点共线,则____________.
三、解答题
17、已知,是平面内两个不共线的非零向量,,,,且A,E,C三点共线.
(1)求实数的值;
(2)若,,求的坐标;
(3)已知,在(2)的条件下,若A,B,C,D四点按逆时针顺序构成平行四边形,求点A的坐标.
18、如图所示,在中,.
(1)用表示;
(2)M为内一点,且,证明:B,M,E三点共线.
19、已知直线,点是直线l上的两点.
(1)若为零向量,求x,y的值;
(2)若为单位向量,求x,y的值.
20、已知.设,且.
(1)求;
(2)求满足的实数m,n;
(3)求点M,N的坐标及的坐标.
参考答案
1、答案:B
解析:根据题意得,,所以,所以,所以.又因为,所以即所以,故选B.
2、答案:B
解析:如图,过点D分别作AC,AB的平行线,交AB,AC于E,F,则四边形AEDF为平行四边形,
所以,因为,所以,
,所以.故选B.
3、答案:C
解析:由知点O到A,B,C三点的距离相等,所以O为的外心.由,知.设AB的中点为D,则,
所以点N在的中线AD上且,所以N为的重心.由,得,即,所以,
同理可得,,所以P为的垂心.故选C.
4、答案:A
解析:如图所示,可得,,且,
所以,为等边三角形,
所以,即每根绳子的拉力大小为10N.
故选:A.
5、答案:B
解析:O是正的中心,
向量,,分别是以三角形的中心和顶点为起点和终点的,
O是正三角形的中心,
O到三个顶点的距离相等,
即,
故选:B.
6、答案:D
解析:由得,,或,
,,从而.
故选:D.
7、答案:A
解析:设,则,,因,
从而有,解得,
所以P点的坐标为.
故选:A.
8、答案:D
解析:因为D是BC的中点,由向量的平行四边形法则可得:,
故选:D.
9、答案:B
解析:由图可知六边形ABCDEF是正六边形,所以,与方向相同的只有;而,,与长度相等,方向不同,所以选项A,C,D,均错误;
故选:B
10、答案:C
解析:由题意知,AC为的外接圆的直径.
设△ABC的外接圆圆心为O,如图,连接OD,BD,则.
所以,
因为,
所以,
所以,
因为.
所以四边形ABDO是平行四边形,
所以,
故选:C.
11、答案:
解析:, 由, 得, 解得.
12、答案:
解析:因为向量,,且,
所以,解得.
故答案为:.
13、答案:
解析:因为,所以,所以.
14、答案:
解析:设,则,即,解得,
所以.
故答案为:.
15、答案:6
解析:设三个力,,分别对于的向量为:,,,
则由题知,
所以,
所以,
又,,,
所以,
所以的大小为:6.
故答案为:6.
16、答案:5
解析:由A,B,C三点共线知,则,解得.
故答案为:5.
17、
(1)答案:
解析:.
因为A,E,C三点共线,所以存在实数k,使得,
即,得.
因为,是平面内两个不共线的非零向量,所以,解得,.
(2)答案:
解析:.
(3)答案:
解析:因为A,B,C,D四点按逆时针顺序构成平行四边形,所以.
设,则,
因为,所以解得,即点A的坐标为.
18、答案:(1);
(2)见解析
解析:(1)因为,所以,
所以.
因为,所以,所以.
(2)因为,所以.
因为,所以,即与共线.
因为与有公共点B,所以B,M,E三点共线.
19、答案:(1)
(2)或
解析:(1)当为零向量时,点B与点A重合,此时.
(2)当为单位向量时,,即点A与点B之间的距离为1,
所以,即,
将代入,化简得,
所以或.
20、答案:(1)
(2)
(3);;
解析:(1)由已知得.
.
(2),
解得
(3),
.
又,
.
.
