2022-2023学年人教B版(2019)必修二 第五章统计与概率 单元测试卷(含解析)
文档属性
| 名称 | 2022-2023学年人教B版(2019)必修二 第五章统计与概率 单元测试卷(含解析) | 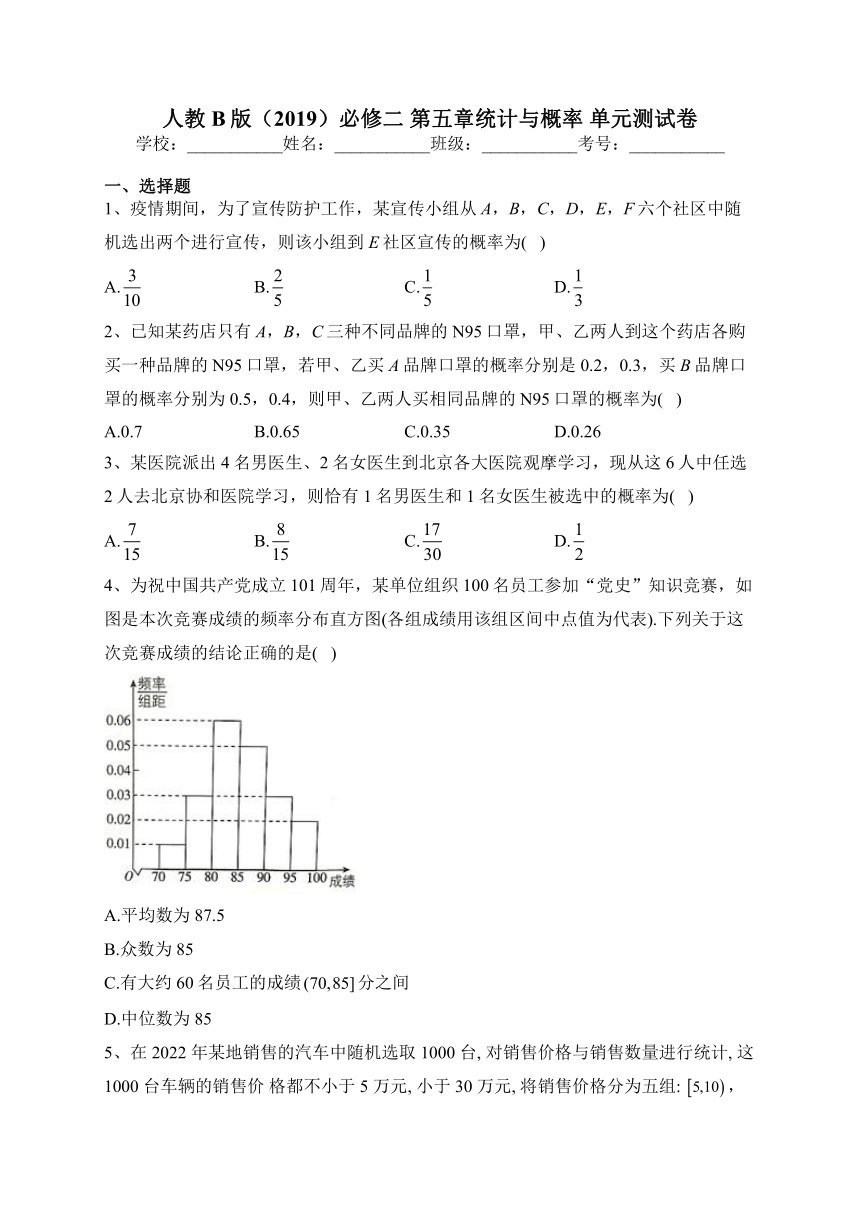 | |
| 格式 | docx | ||
| 文件大小 | 419.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-05 16:51:18 | ||
图片预览





文档简介
人教B版(2019)必修二 第五章统计与概率 单元测试卷
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1、疫情期间,为了宣传防护工作,某宣传小组从A,B,C,D,E,F六个社区中随机选出两个进行宣传,则该小组到E社区宣传的概率为( )
A. B. C. D.
2、已知某药店只有A,B,C三种不同品牌的N95口罩,甲、乙两人到这个药店各购买一种品牌的N95口罩,若甲、乙买A品牌口罩的概率分别是0.2,0.3,买B品牌口罩的概率分别为0.5,0.4,则甲、乙两人买相同品牌的N95口罩的概率为( )
A.0.7 B.0.65 C.0.35 D.0.26
3、某医院派出4名男医生、2名女医生到北京各大医院观摩学习,现从这6人中任选2人去北京协和医院学习,则恰有1名男医生和1名女医生被选中的概率为( )
A. B. C. D.
4、为祝中国共产党成立101周年,某单位组织100名员工参加“党史”知识竞赛,如图是本次竞赛成绩的频率分布直方图(各组成绩用该组区间中点值为代表).下列关于这次竞赛成绩的结论正确的是( )
A.平均数为87.5
B.众数为85
C.有大约60名员工的成绩分之间
D.中位数为85
5、在 2022 年某地销售的汽车中随机选取 1000 台, 对销售价格与销售数量进行统计, 这 1000 台车辆的销售价 格都不小于 5 万元, 小于 30 万元, 将销售价格分为五组: ,,,,(单位: 万元). 统计后制成的频率分布直方图如图所示. 在选取的 1000 台汽车中, 销售价格在 内的车辆台数为( )
A. 800 B. 600 C. 700 D. 750
6、如图所示的茎叶图记录了甲、乙两组各5名工人某日的产量数据(单位:件).若这两组数据的中位数相等,且平均值也相等,则x和y的值分别为( )
A.3,5 B.5,5 C.3,7 D.5,7
7、某校有文科教师120名,理科教师150名,其性别比例如图所示,则该校女教师的人数为( )
A.96 B.126 C.144 D.174
8、某学校高中部准备在“五四”青年节举行主题为“成长、感恩、责任、梦想”的十八岁成人仪式,其中有一项学生发言,现从5名男生干部、3名女生干部中选取3人发言,则选取的3人中既有男生又有女生的概率为( )
A. B. C. D.
9、2019年10月1日,在庆祝中华人民共和国成立70周年大阅兵的徒步方队中,被誉为“最强大脑”的院校科研方队队员分别由军事科学院、国防大学、国防科技大学三所院校联合抽组,已知军事科学院的甲、乙、丙三名同学被选上的概率分别为,,,则这三名同学中至少有一名同学被选上的概率为( )
A. B. C. D.
10、5G手机是指使用第五代通信系统的智能手机,已经面市.相对4G手机,5G手机有更快的网络与通信,低时延,通过网络切片技术,拥有更精准的定位.这也导致了越来越多的人喜欢用手机上网.某学校为了调查该校学生使用手机上网的时间,随机抽取了200名学生,对他们每天使用手机上网的时间进行统计,并将得到的数据制成频率分布直方图,如图.其中使用手机上网的时间范围为,则下列叙述正确的是( )
A.a的值为0.06
B.上网时间在5~10min的频率为0.04
C.上网时间在15~20min的频数为30
D.上网时间的平均数为15min
二、填空题
11、为了了解某市不同年龄的居民对“执行垃圾分类”的看法,现从该市某小区随机抽查了年龄在10~70岁的100名住户,绘制出频率分布直方图如图所示,则所抽取的这100名住户的年龄的中位数为__________.
12、从某项综合能力测试中抽取100人的成绩,统计如表,则这100人成绩的标准差为__________.
分数 5 4 3 2 1
人数 20 10 30 30 10
13、已知甲同学6次数学期中考试的成绩如下表所示:
年级 高一(上) 高一(下) 高二(上) 高二(下) 高三(上) 高三(下)
成绩 120 115 135 98 130 125
则该同学6次数学考试成绩的中位数为___________.
14、已知一组样本数据,,…,,且,均数,则该组数据的标准差为_________.
15、一个志愿者组织有男,女成员84人.其中48名男成员中,45岁以上的有12人;36名女成员中,45岁以上的有18人.根据需要,按照年龄进行分层抽样,要从这个志愿者组织成员中抽取28人开展活动,则45岁以上的成员应抽取___________人.
16、为强化安全意识,某校拟在周一至周五的五天中随机选择2天进行紧急疏散演练,则选择的2天恰好为连续2天的概率是__________.
三、解答题
17、20.某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:,,,后得到如图的频率分布直方图.
(1)求图中实数的值;
(2)若该校高一年级共有学生1000人,试估计该校高一年级期中考试数学成绩不低于60分的人数.
(3)若从样本中数学成绩在与两个分数段内的学生中随机选取2名学生,试用列举法求这2名学生的数学成绩之差的绝对值大于10的槪率.
18、甲、乙两人在相同条件下各射击10次,每次命中的环数如下:
甲 8 6 7 8 6 5 9 10 4 7
乙 6 7 7 8 6 7 8 7 9 5
(1)分别计算以上两组数据的平均数;
(2)分别计算以上两组数据的方差;
(3)根据计算结果,对甲乙两人的射击成绩作出评价.
19、为了对某课题进行研究,分别从A,B,C三所高校中用分层随机抽样法(样本量按比例分配)抽取若干名教授组成研究小组,其中高校A有m名教授,高校B有72名教授,高校C有n名教授(其中).
(1)若A,B两所高校中共抽取3名教授,B,C两所高校中共抽取5名教授,求m,n;
(2)若高校B中抽取的教授数是高校A和C中抽取的教授总数的,求三所高校的教授的总人数.
20、某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如表所示:
上年度出险次数 0 1 2 3 4
保费 a
随机调查了该险种的200名续保人在一年内的出险情况,得到统计表:
出险次数 0 1 2 3 4
频数 60 50 30 30 20 10
(1)记A为事件:“一续保人本年度的保费不高于基本保费”,求的估计值.
(2)记B为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的160%”.求的估计值.
(3)求续保人本年度平均保费的估计值.
参考答案
1、答案:D
解析:从A,B,C,D,E,F六个社区中随机选出两个的结果有,,,,,,,,,,,,,,,共15种,其中该小组到E社区宣传的结果有,,,,,共5种,因此所求概率为.
2、答案:C
解析:由题意,得甲、乙两人买C品牌口罩的概率都是0.3,所以甲、乙两人买相同品牌的N95口罩的概率为.故选C.
3、答案:B
解析:设4名男医生分别为a,b,c,d,2名女医生分别为A,B,则从中任选2人有,,,,,,,,,,,,,,,共15个基本事件,其中恰有1名男医生和1名女医生的有,,,,,,,,共8个基本事件,因此所求概率.故选B.
4、答案:D
解析:由平均数计算公式得,A错误;众数出现在之间,故众数为82.5,B错误;由,有50名员工的成绩在分之间,C错误;由,即中位数为85,D正确.
5、答案:C
解析:由频率分布直方图知, , 所以, 所以销售 价格在内的频率为, 故销售价格在内的车辆台数为
6、答案:A
解析:由题意,甲组数据为56,62,65,,74,乙组数据为59,61,67,,78.要使两组数据中位数相等,有,,又平均数相同,则,解得.故选A.
7、答案:C
解析:该校文科女教师的人数为,理科女教师的人数为,所以该校女教师的人数为144.故选C.
8、答案:D
解析:选取的3人中既有男生又有女生的概率.故选D.
9、答案:C
解析:记“这三名同学中至少有一名同学被选上”为事件A,
则事件为“这三名同学都没被选上”,则,所以.故选C.
10、答案:A
解析:由题图可得,所以,故A正确;上网时间在5~10min的频率为,故B错误;上网时间在15~20min的频率为,则频数为,故C错误;上网时间的平均数为(min),故D错误.故选A.
11、答案:
解析:设所抽取的这100名住户的年龄的中位数为m,
则有,
解得.
12、答案:
解析:因为,
所以
,所以.
13、答案:122.5
解析:将该同学6次数学考试成绩按照从小到大排列可得98,115,120,125,130,135,可得中位数为122.5,
故答案为:122.5.
14、答案:9
解析:一组样本数据,,...,,且,平均数,
则该组数据的方差为
.
该组数据的标准差为9.故答案为:9.
15、答案:10
解析:依题意按照分层抽样45岁以上的成员应抽取(人);
故答案为:10
16、答案:
解析:考查古典概型的计算公式及分析问题解决问题的能力.从5个元素a,b,c,d,e中选2个的所有可能有10种,其中连续有ab,bc,cd,de共4种,故由古典概型的计算公式可知恰好为连续2天的概率是.
17、
(1)答案:
解析:由频率分布直方图,得:,解得.
(2)答案:850
解析:数学成绩不低于60分的概率为:,数学成绩不低于60分的人数为:(人).
(3)答案:
解析:数学成绩在的学生为40×0.05=2(人),数学成绩在的学生人数为(人),设数学成绩在的学生为A,B,数学成绩在的学生为a,b,c,d,从样本中数学成绩在与两个分数段内的学生中随机选取2名学生,基本事件有:,,,,,,,,,,,,,,
其中两名学生的数学成绩之差的绝对值大于10的情况有:
,,,,,,,,共8种,
这2名学生的数学成绩之差的绝对值大于10的槪率为.
18、答案: (1)7;7(2)3;2(3)乙的射击水平要比甲的射击水平更稳定
解析:(1)甲的平均分为:,
乙的平均分为:.
(2)甲的方差为:
,
乙的方差为:
(3)甲、乙的平均分相同,说明甲、乙两人射击的平均水平相当,又,说明乙的射击水平要比甲的射击水平更稳定.
19、答案:(1),
(2)三所高校的教授的总人数为180
解析:(1),A,B两所高校中共抽取3名教授,B,C两所高校中共抽取5名教授,高校B中抽取2名教授,高校A中抽取1名教授,高校C中抽取3名教授,
,解得,.
(2)高校B中抽取的教授数是高校A和C中抽取的教授总数的,
,解得,
三所高校的教授的总人数为.
20、答案:(1)的估计值为0.55
(2)的估计值为0.3
(3)估计值为
解析:(1)事件A发生当且仅当一年内出险次数小于2.
由所给数据知,一年内出险次数小于2的频率为,
故的估计值为0.55.
(2)事件B发生当且仅当一年内出险次数大于1且小于4.
由所给数据知,一年内出险次数大于1且小于4的频率为:,
故的估计值为0.3.
(3)由所给数据得
保费 a
频率 0.30 0.25 0.15 0.15 0.10 0.05
调查的200名续保人的平均保费为.
因此,续保人本年度平均保费的估计值为.
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1、疫情期间,为了宣传防护工作,某宣传小组从A,B,C,D,E,F六个社区中随机选出两个进行宣传,则该小组到E社区宣传的概率为( )
A. B. C. D.
2、已知某药店只有A,B,C三种不同品牌的N95口罩,甲、乙两人到这个药店各购买一种品牌的N95口罩,若甲、乙买A品牌口罩的概率分别是0.2,0.3,买B品牌口罩的概率分别为0.5,0.4,则甲、乙两人买相同品牌的N95口罩的概率为( )
A.0.7 B.0.65 C.0.35 D.0.26
3、某医院派出4名男医生、2名女医生到北京各大医院观摩学习,现从这6人中任选2人去北京协和医院学习,则恰有1名男医生和1名女医生被选中的概率为( )
A. B. C. D.
4、为祝中国共产党成立101周年,某单位组织100名员工参加“党史”知识竞赛,如图是本次竞赛成绩的频率分布直方图(各组成绩用该组区间中点值为代表).下列关于这次竞赛成绩的结论正确的是( )
A.平均数为87.5
B.众数为85
C.有大约60名员工的成绩分之间
D.中位数为85
5、在 2022 年某地销售的汽车中随机选取 1000 台, 对销售价格与销售数量进行统计, 这 1000 台车辆的销售价 格都不小于 5 万元, 小于 30 万元, 将销售价格分为五组: ,,,,(单位: 万元). 统计后制成的频率分布直方图如图所示. 在选取的 1000 台汽车中, 销售价格在 内的车辆台数为( )
A. 800 B. 600 C. 700 D. 750
6、如图所示的茎叶图记录了甲、乙两组各5名工人某日的产量数据(单位:件).若这两组数据的中位数相等,且平均值也相等,则x和y的值分别为( )
A.3,5 B.5,5 C.3,7 D.5,7
7、某校有文科教师120名,理科教师150名,其性别比例如图所示,则该校女教师的人数为( )
A.96 B.126 C.144 D.174
8、某学校高中部准备在“五四”青年节举行主题为“成长、感恩、责任、梦想”的十八岁成人仪式,其中有一项学生发言,现从5名男生干部、3名女生干部中选取3人发言,则选取的3人中既有男生又有女生的概率为( )
A. B. C. D.
9、2019年10月1日,在庆祝中华人民共和国成立70周年大阅兵的徒步方队中,被誉为“最强大脑”的院校科研方队队员分别由军事科学院、国防大学、国防科技大学三所院校联合抽组,已知军事科学院的甲、乙、丙三名同学被选上的概率分别为,,,则这三名同学中至少有一名同学被选上的概率为( )
A. B. C. D.
10、5G手机是指使用第五代通信系统的智能手机,已经面市.相对4G手机,5G手机有更快的网络与通信,低时延,通过网络切片技术,拥有更精准的定位.这也导致了越来越多的人喜欢用手机上网.某学校为了调查该校学生使用手机上网的时间,随机抽取了200名学生,对他们每天使用手机上网的时间进行统计,并将得到的数据制成频率分布直方图,如图.其中使用手机上网的时间范围为,则下列叙述正确的是( )
A.a的值为0.06
B.上网时间在5~10min的频率为0.04
C.上网时间在15~20min的频数为30
D.上网时间的平均数为15min
二、填空题
11、为了了解某市不同年龄的居民对“执行垃圾分类”的看法,现从该市某小区随机抽查了年龄在10~70岁的100名住户,绘制出频率分布直方图如图所示,则所抽取的这100名住户的年龄的中位数为__________.
12、从某项综合能力测试中抽取100人的成绩,统计如表,则这100人成绩的标准差为__________.
分数 5 4 3 2 1
人数 20 10 30 30 10
13、已知甲同学6次数学期中考试的成绩如下表所示:
年级 高一(上) 高一(下) 高二(上) 高二(下) 高三(上) 高三(下)
成绩 120 115 135 98 130 125
则该同学6次数学考试成绩的中位数为___________.
14、已知一组样本数据,,…,,且,均数,则该组数据的标准差为_________.
15、一个志愿者组织有男,女成员84人.其中48名男成员中,45岁以上的有12人;36名女成员中,45岁以上的有18人.根据需要,按照年龄进行分层抽样,要从这个志愿者组织成员中抽取28人开展活动,则45岁以上的成员应抽取___________人.
16、为强化安全意识,某校拟在周一至周五的五天中随机选择2天进行紧急疏散演练,则选择的2天恰好为连续2天的概率是__________.
三、解答题
17、20.某校从高一年级学生中随机抽取40名学生,将他们的期中考试数学成绩(满分100分,成绩均为不低于40分的整数)分成六段:,,,后得到如图的频率分布直方图.
(1)求图中实数的值;
(2)若该校高一年级共有学生1000人,试估计该校高一年级期中考试数学成绩不低于60分的人数.
(3)若从样本中数学成绩在与两个分数段内的学生中随机选取2名学生,试用列举法求这2名学生的数学成绩之差的绝对值大于10的槪率.
18、甲、乙两人在相同条件下各射击10次,每次命中的环数如下:
甲 8 6 7 8 6 5 9 10 4 7
乙 6 7 7 8 6 7 8 7 9 5
(1)分别计算以上两组数据的平均数;
(2)分别计算以上两组数据的方差;
(3)根据计算结果,对甲乙两人的射击成绩作出评价.
19、为了对某课题进行研究,分别从A,B,C三所高校中用分层随机抽样法(样本量按比例分配)抽取若干名教授组成研究小组,其中高校A有m名教授,高校B有72名教授,高校C有n名教授(其中).
(1)若A,B两所高校中共抽取3名教授,B,C两所高校中共抽取5名教授,求m,n;
(2)若高校B中抽取的教授数是高校A和C中抽取的教授总数的,求三所高校的教授的总人数.
20、某险种的基本保费为a(单位:元),继续购买该险种的投保人称为续保人,续保人本年度的保费与其上年度出险次数的关联如表所示:
上年度出险次数 0 1 2 3 4
保费 a
随机调查了该险种的200名续保人在一年内的出险情况,得到统计表:
出险次数 0 1 2 3 4
频数 60 50 30 30 20 10
(1)记A为事件:“一续保人本年度的保费不高于基本保费”,求的估计值.
(2)记B为事件:“一续保人本年度的保费高于基本保费但不高于基本保费的160%”.求的估计值.
(3)求续保人本年度平均保费的估计值.
参考答案
1、答案:D
解析:从A,B,C,D,E,F六个社区中随机选出两个的结果有,,,,,,,,,,,,,,,共15种,其中该小组到E社区宣传的结果有,,,,,共5种,因此所求概率为.
2、答案:C
解析:由题意,得甲、乙两人买C品牌口罩的概率都是0.3,所以甲、乙两人买相同品牌的N95口罩的概率为.故选C.
3、答案:B
解析:设4名男医生分别为a,b,c,d,2名女医生分别为A,B,则从中任选2人有,,,,,,,,,,,,,,,共15个基本事件,其中恰有1名男医生和1名女医生的有,,,,,,,,共8个基本事件,因此所求概率.故选B.
4、答案:D
解析:由平均数计算公式得,A错误;众数出现在之间,故众数为82.5,B错误;由,有50名员工的成绩在分之间,C错误;由,即中位数为85,D正确.
5、答案:C
解析:由频率分布直方图知, , 所以, 所以销售 价格在内的频率为, 故销售价格在内的车辆台数为
6、答案:A
解析:由题意,甲组数据为56,62,65,,74,乙组数据为59,61,67,,78.要使两组数据中位数相等,有,,又平均数相同,则,解得.故选A.
7、答案:C
解析:该校文科女教师的人数为,理科女教师的人数为,所以该校女教师的人数为144.故选C.
8、答案:D
解析:选取的3人中既有男生又有女生的概率.故选D.
9、答案:C
解析:记“这三名同学中至少有一名同学被选上”为事件A,
则事件为“这三名同学都没被选上”,则,所以.故选C.
10、答案:A
解析:由题图可得,所以,故A正确;上网时间在5~10min的频率为,故B错误;上网时间在15~20min的频率为,则频数为,故C错误;上网时间的平均数为(min),故D错误.故选A.
11、答案:
解析:设所抽取的这100名住户的年龄的中位数为m,
则有,
解得.
12、答案:
解析:因为,
所以
,所以.
13、答案:122.5
解析:将该同学6次数学考试成绩按照从小到大排列可得98,115,120,125,130,135,可得中位数为122.5,
故答案为:122.5.
14、答案:9
解析:一组样本数据,,...,,且,平均数,
则该组数据的方差为
.
该组数据的标准差为9.故答案为:9.
15、答案:10
解析:依题意按照分层抽样45岁以上的成员应抽取(人);
故答案为:10
16、答案:
解析:考查古典概型的计算公式及分析问题解决问题的能力.从5个元素a,b,c,d,e中选2个的所有可能有10种,其中连续有ab,bc,cd,de共4种,故由古典概型的计算公式可知恰好为连续2天的概率是.
17、
(1)答案:
解析:由频率分布直方图,得:,解得.
(2)答案:850
解析:数学成绩不低于60分的概率为:,数学成绩不低于60分的人数为:(人).
(3)答案:
解析:数学成绩在的学生为40×0.05=2(人),数学成绩在的学生人数为(人),设数学成绩在的学生为A,B,数学成绩在的学生为a,b,c,d,从样本中数学成绩在与两个分数段内的学生中随机选取2名学生,基本事件有:,,,,,,,,,,,,,,
其中两名学生的数学成绩之差的绝对值大于10的情况有:
,,,,,,,,共8种,
这2名学生的数学成绩之差的绝对值大于10的槪率为.
18、答案: (1)7;7(2)3;2(3)乙的射击水平要比甲的射击水平更稳定
解析:(1)甲的平均分为:,
乙的平均分为:.
(2)甲的方差为:
,
乙的方差为:
(3)甲、乙的平均分相同,说明甲、乙两人射击的平均水平相当,又,说明乙的射击水平要比甲的射击水平更稳定.
19、答案:(1),
(2)三所高校的教授的总人数为180
解析:(1),A,B两所高校中共抽取3名教授,B,C两所高校中共抽取5名教授,高校B中抽取2名教授,高校A中抽取1名教授,高校C中抽取3名教授,
,解得,.
(2)高校B中抽取的教授数是高校A和C中抽取的教授总数的,
,解得,
三所高校的教授的总人数为.
20、答案:(1)的估计值为0.55
(2)的估计值为0.3
(3)估计值为
解析:(1)事件A发生当且仅当一年内出险次数小于2.
由所给数据知,一年内出险次数小于2的频率为,
故的估计值为0.55.
(2)事件B发生当且仅当一年内出险次数大于1且小于4.
由所给数据知,一年内出险次数大于1且小于4的频率为:,
故的估计值为0.3.
(3)由所给数据得
保费 a
频率 0.30 0.25 0.15 0.15 0.10 0.05
调查的200名续保人的平均保费为.
因此,续保人本年度平均保费的估计值为.
