2022-2023学年人教B版(2019)必修三 第七章 三角函数 单元测试卷(含解析)
文档属性
| 名称 | 2022-2023学年人教B版(2019)必修三 第七章 三角函数 单元测试卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 646.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-05 16:52:32 | ||
图片预览


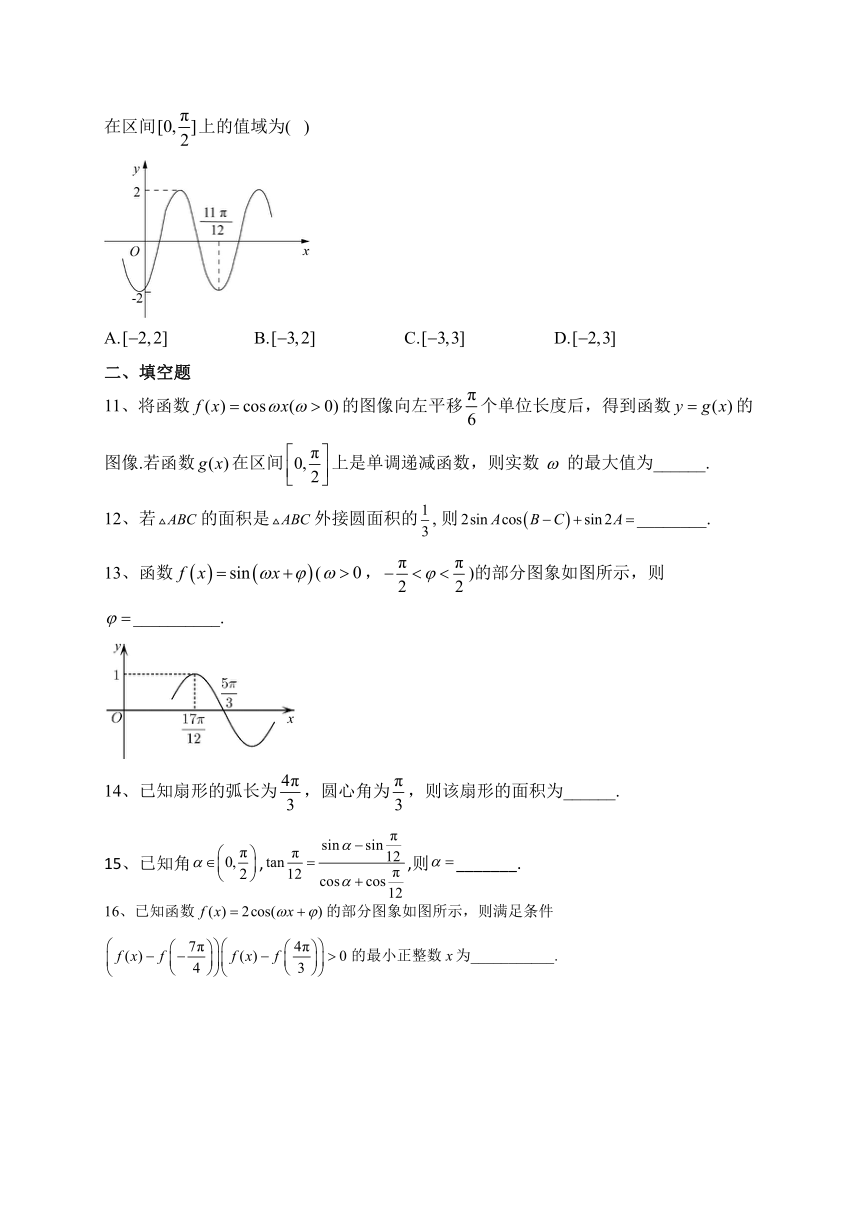


文档简介
人教B版(2019)必修三 第七章 三角函数 单元测试卷
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1、设函数,,,若在区间上单调,且,则的最小正周期为( )
A. B. C. D.
2、已知函数(,)的部分图象如图所示,记方程在内所有解的和为,则( )
A. B. C. D.
3、已知函数(,)的最小正周期为,若先将的图象向左平移个单位长度,再将所得图象上各点的横坐标缩短为原来的,得到函数的图象,且函数图象的一条对称轴方程是,则的值为( )
A.0 B. C. D.
4、已知函数的图象向右平移个单位长度后得到函数的图象,且,则( )
A. B. C. D.
5、已知,,,则( )
A. B. C. D.
6、设,,且满足,则的取值范围为( )
A. B. C. D.
7、已知, 则 ( )
A. B. C. D.
8、已知函数,将函数的图象向右平移个单位后与函数的图象重合,则的值可以是( )
A. B. C. D.
9、函数的部分图象如图所示,且,则图中m的值为( )
A.1 B. C.2 D.或2
10、已知函数(,)部分图象如图所示,则函数在区间上的值域为( )
A. B. C. D.
二、填空题
11、将函数的图像向左平移个单位长度后,得到函数的图像.若函数在区间上是单调递减函数,则实数的最大值为______.
12、若的面积是外接圆面积的, 则________.
13、函数(,)的部分图象如图所示,则__________.
14、已知扇形的弧长为,圆心角为,则该扇形的面积为______.
15、已知角,,则_______.
16、已知函数的部分图象如图所示,则满足条件的最小正整数x为___________.
三、解答题
17、如图,某年某动物种群数量1月1日低至700,7月1日高至900,其总量在此两值之间依正弦型曲线变化.
(1)求出种群数量y关于时间t的函数表达式.
(2)猜测当年3月1日该动物的种群数量.
18、一只红蚂蚁与一只黑蚂蚁在一个单位圆(半径为1的圆)上爬动,若两只蚂蚁均从点同时逆时针匀速爬动,若红蚂蚁每秒爬过角,黑蚂蚁每秒爬过角(其中),如果两只蚂蚁都在第14秒时回到A点,并且在第2秒时均位于第二象限,求的值.
19、已知.
(1)化简.
(2)若,求的值.
(3)若,,求的值.
20、已知函数.其图象的一个对称中心是,将的图象向左平移个单位长度后得到函数的图象.
(1)求函数的解析式;
(2)若对任意,当时,都有,求实数t的最大值.
参考答案
1、答案:D
解析:因为在区间上单调,,所以,所以.又因为,所以直线为图象的一条对称轴;因为,所以为图象的一个对称中心.因为,所以直线与为同一周期里相邻的对称轴和对称中心,所以.故选D.
2、答案:C
解析:设的最小正周期为T,由题图可知,,解得,,,.的图象过点,,,解得,,,.令,得,解得,其中落在区间内的解有,,故.故选C.
3、答案:A
解析:由函数的最小正周期为得,则.
将的图象向左平移个单位长度,所得图象对应的函数解析式为,再将所得图象上各点的横坐标缩短为原来的,所得图象对应的函数解析式为,则,,得,,又,所以,故选A.
4、答案:B
解析:由题意可知,函数.因为,所以函数为奇函数,则,.又,令,则,所以函数,
,故选B.
5、答案:B
解析:略
6、答案:B
解析:,又,,则,
所以,所以,
故选:B.
7、答案:B
解析:由,两边平方得, , 从而.
8、答案:A
解析:依题意,,故,则.故选A.
9、答案:B
解析:,且,,,,,,,.又函数的最小正周期,,.
10、答案:B
解析:由图易知,为“五点作图法”中的第四点,所以,解得,则.由,得,则,
,即函数在区间上的值域为.故选B.
11、答案:
解析:本题考查三角函数的图像与性质以及函数图像的变换.由题意,将函数的图像向左平移个单位长度,得到函数的图像,若函数在区间上是单调递减函数,因为,所以,所以,则,所以,则,取,则,则解得,所以实数的最大值为.
12、答案:
解析:因为, 所以, 由正弦定理得 ,,所以, 所以,
又
13、答案:
解析:解:由图象可知:的最小正周期,,
,(),
(),
因为,所以.
故答案为:.
14、答案:
15、答案:
解析:,,
,
,
,
,,
,则.
故答案为:.
16、答案:2
解析:本题考查三角函数的图象、性质,不等式.由已知可知的周期T满足,故,.由,可令.故,所以,,原不等式化为,可得或.结合图象,若x取正数,①当时,,此时没有满足条件的正整数;②当时,,此时满足条件的最小正整数为2.
17、答案:(1)(答案不唯一)
(2)750
解析:(1)设种群数量y关于时间t的表达式为(,,),
则,解得,.
又周期,,.
又当时,,,
,,可取,
.(答案不唯一)
(2)当时,,即当年3月1日该动物种群数量约是750.
18、答案:,
解析:据题意可知:,均为360°的整数倍,故可设,,,,从而可知,,.
又由两只蚂蚁在第2秒时均位于第二象限,则,在第二象限.
又,从而可得,
因此,均为钝角,即.
于是,.
,,
即,.
又,,从而可得,.
即,.
19、
(1)答案:见解析
解析:
(2)答案:
解析:若,则
(3)答案:
解析:由,可得,因为,所以,所以.
20、
(1)答案:
解析:由题意,得,解得,
又,,,
从而.
(2)答案:t的最大值为
解析:对任意,且,
,
即在上单调递增,
,
由,得,
即的单调增区间为,
由于,
当时,,从而,
实数t的最大值为.
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1、设函数,,,若在区间上单调,且,则的最小正周期为( )
A. B. C. D.
2、已知函数(,)的部分图象如图所示,记方程在内所有解的和为,则( )
A. B. C. D.
3、已知函数(,)的最小正周期为,若先将的图象向左平移个单位长度,再将所得图象上各点的横坐标缩短为原来的,得到函数的图象,且函数图象的一条对称轴方程是,则的值为( )
A.0 B. C. D.
4、已知函数的图象向右平移个单位长度后得到函数的图象,且,则( )
A. B. C. D.
5、已知,,,则( )
A. B. C. D.
6、设,,且满足,则的取值范围为( )
A. B. C. D.
7、已知, 则 ( )
A. B. C. D.
8、已知函数,将函数的图象向右平移个单位后与函数的图象重合,则的值可以是( )
A. B. C. D.
9、函数的部分图象如图所示,且,则图中m的值为( )
A.1 B. C.2 D.或2
10、已知函数(,)部分图象如图所示,则函数在区间上的值域为( )
A. B. C. D.
二、填空题
11、将函数的图像向左平移个单位长度后,得到函数的图像.若函数在区间上是单调递减函数,则实数的最大值为______.
12、若的面积是外接圆面积的, 则________.
13、函数(,)的部分图象如图所示,则__________.
14、已知扇形的弧长为,圆心角为,则该扇形的面积为______.
15、已知角,,则_______.
16、已知函数的部分图象如图所示,则满足条件的最小正整数x为___________.
三、解答题
17、如图,某年某动物种群数量1月1日低至700,7月1日高至900,其总量在此两值之间依正弦型曲线变化.
(1)求出种群数量y关于时间t的函数表达式.
(2)猜测当年3月1日该动物的种群数量.
18、一只红蚂蚁与一只黑蚂蚁在一个单位圆(半径为1的圆)上爬动,若两只蚂蚁均从点同时逆时针匀速爬动,若红蚂蚁每秒爬过角,黑蚂蚁每秒爬过角(其中),如果两只蚂蚁都在第14秒时回到A点,并且在第2秒时均位于第二象限,求的值.
19、已知.
(1)化简.
(2)若,求的值.
(3)若,,求的值.
20、已知函数.其图象的一个对称中心是,将的图象向左平移个单位长度后得到函数的图象.
(1)求函数的解析式;
(2)若对任意,当时,都有,求实数t的最大值.
参考答案
1、答案:D
解析:因为在区间上单调,,所以,所以.又因为,所以直线为图象的一条对称轴;因为,所以为图象的一个对称中心.因为,所以直线与为同一周期里相邻的对称轴和对称中心,所以.故选D.
2、答案:C
解析:设的最小正周期为T,由题图可知,,解得,,,.的图象过点,,,解得,,,.令,得,解得,其中落在区间内的解有,,故.故选C.
3、答案:A
解析:由函数的最小正周期为得,则.
将的图象向左平移个单位长度,所得图象对应的函数解析式为,再将所得图象上各点的横坐标缩短为原来的,所得图象对应的函数解析式为,则,,得,,又,所以,故选A.
4、答案:B
解析:由题意可知,函数.因为,所以函数为奇函数,则,.又,令,则,所以函数,
,故选B.
5、答案:B
解析:略
6、答案:B
解析:,又,,则,
所以,所以,
故选:B.
7、答案:B
解析:由,两边平方得, , 从而.
8、答案:A
解析:依题意,,故,则.故选A.
9、答案:B
解析:,且,,,,,,,.又函数的最小正周期,,.
10、答案:B
解析:由图易知,为“五点作图法”中的第四点,所以,解得,则.由,得,则,
,即函数在区间上的值域为.故选B.
11、答案:
解析:本题考查三角函数的图像与性质以及函数图像的变换.由题意,将函数的图像向左平移个单位长度,得到函数的图像,若函数在区间上是单调递减函数,因为,所以,所以,则,所以,则,取,则,则解得,所以实数的最大值为.
12、答案:
解析:因为, 所以, 由正弦定理得 ,,所以, 所以,
又
13、答案:
解析:解:由图象可知:的最小正周期,,
,(),
(),
因为,所以.
故答案为:.
14、答案:
15、答案:
解析:,,
,
,
,
,,
,则.
故答案为:.
16、答案:2
解析:本题考查三角函数的图象、性质,不等式.由已知可知的周期T满足,故,.由,可令.故,所以,,原不等式化为,可得或.结合图象,若x取正数,①当时,,此时没有满足条件的正整数;②当时,,此时满足条件的最小正整数为2.
17、答案:(1)(答案不唯一)
(2)750
解析:(1)设种群数量y关于时间t的表达式为(,,),
则,解得,.
又周期,,.
又当时,,,
,,可取,
.(答案不唯一)
(2)当时,,即当年3月1日该动物种群数量约是750.
18、答案:,
解析:据题意可知:,均为360°的整数倍,故可设,,,,从而可知,,.
又由两只蚂蚁在第2秒时均位于第二象限,则,在第二象限.
又,从而可得,
因此,均为钝角,即.
于是,.
,,
即,.
又,,从而可得,.
即,.
19、
(1)答案:见解析
解析:
(2)答案:
解析:若,则
(3)答案:
解析:由,可得,因为,所以,所以.
20、
(1)答案:
解析:由题意,得,解得,
又,,,
从而.
(2)答案:t的最大值为
解析:对任意,且,
,
即在上单调递增,
,
由,得,
即的单调增区间为,
由于,
当时,,从而,
实数t的最大值为.
