2022-2023学年人教版数学七年级下册 5.1.1相交线同步练习 (含答案)
文档属性
| 名称 | 2022-2023学年人教版数学七年级下册 5.1.1相交线同步练习 (含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 330.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-06 00:00:00 | ||
图片预览



文档简介
5.1.1相交线
(同步练习)
一、单选题
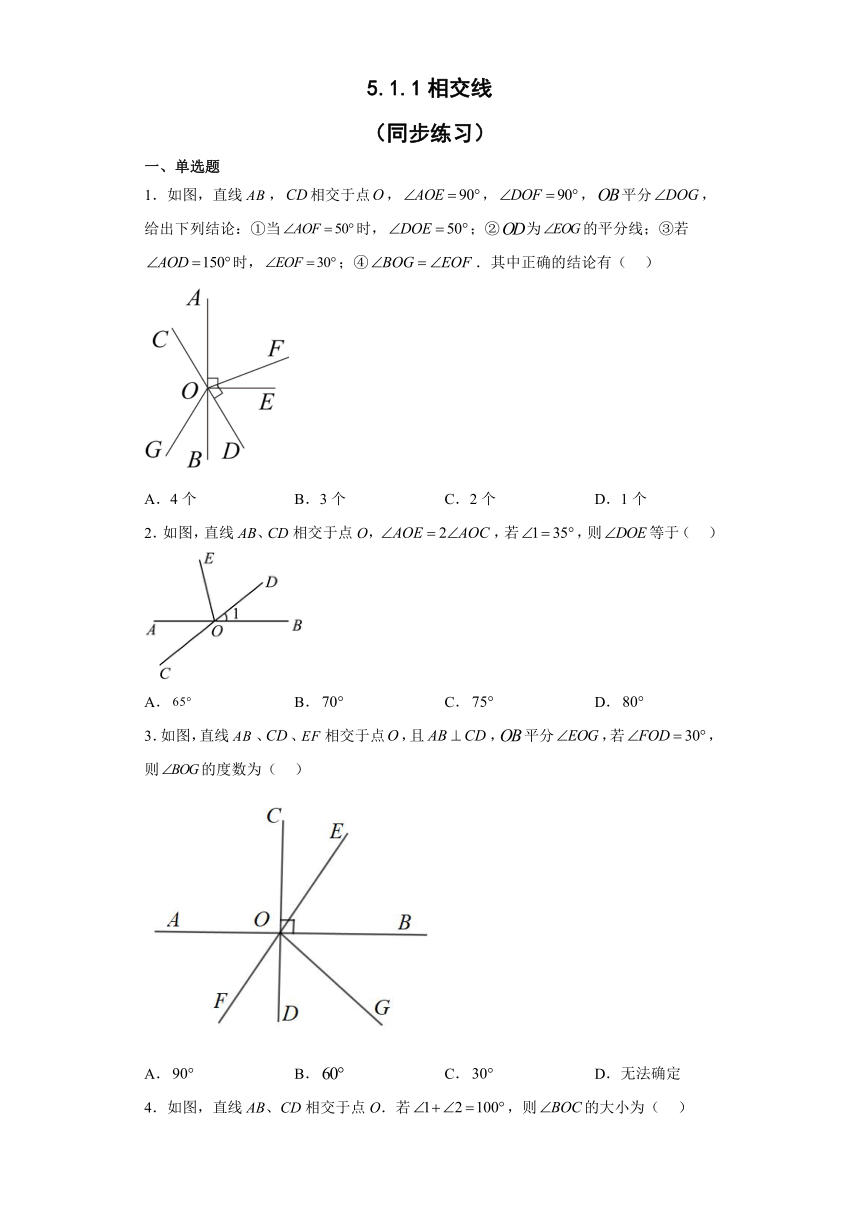
1.如图,直线,相交于点,,,平分,给出下列结论:①当时,;②为的平分线;③若时,;④.其中正确的结论有( )
A.4个 B.3个 C.2个 D.1个
2.如图,直线AB、CD相交于点O,,若,则等于( )
A. B. C. D.
3.如图,直线、、相交于点,且,平分,若,则的度数为( )
A. B. C. D.无法确定
4.如图,直线AB、CD相交于点O.若,则的大小为( )
A. B. C. D.
5.已知各角的度数如图所示,则下列各题中的和分别是( ).
A. B. C. D.
6.如图,已知,则图中与相等的角有( )
A. B. C. D.
7.下列各图中,与是对顶角的是( )
A. B.
C. D.
8.如图,直线相交于点,若,则的度数是( )
A.30° B.40° C.60° D.150°
9.下列说法:①点动成线;②相等的角是对顶角;③同角的余角相等;④两点之间直线最短,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
10.下图中,和是对顶角的是( )
A. B.
C. D.
二、填空题
11.如图直线AB,CD相交于O,直线FE⊥AB于O,∠BOD=75°,则∠COF的度数为_____度.
12.如图,直线、相交,若与互余,则的度数为____________.
13.如图,直线、、相交于点,若,则______
14.已知,直线AB和直线CD交于点O,∠BOD是它的邻补角的3倍,则直线AB与直线CD的夹角是________度.
15.如图,O是直线上一点,,则___.
三、解答题
16.如图,直线AB、CD相交于点O,∠DOE=∠BOD,OF平分∠AOE.
(1)判断OF与OD的位置关系,并说明理由;
(2)若∠AOC:∠AOD=1:5,求∠EOF的度数.
17.如图,直线AB,CD相交于点O,OF⊥CD,OE平分∠BOC.
(1)若∠BOE=65°,求∠DOE的度数;
(2)若∠BOD:∠BOE=2:3,求∠AOF的度数.
18.如图,直线、相交于点,平分,.
(1)若∠AOF=50°,求∠BOE的度数;
(2)若∠BOD:∠BOE=1:4,求∠AOF的度数.
19.如图,直线,,相交于点,平分,.
(1)写出的余角和补角;
(2)若,求和的度数.
20.如图,直线AB与CD相交于点O,OEAB,OFCD.
(1)图中∠AOF的余角是 (把符合条件的角都填出来).
(2)图中除直角相等外,还有相等的角,请写出三对:
① ;② ;③ .
(3)①如果∠AOD=140°.那么根据 ,可得∠BOC= 度.
②如果,求∠EOF的度数.
21.如图所示,直线a,b,c两两相交,,求的度数.
参考答案:
1.B2.C3.B4.C5.B6.D7.D8.A9.B10.B
11.15
12.
13.30
14.45
15.
16.(1)解:OF⊥OD,
理由:∵OF平分∠AOE,
∴∠AOF=∠FOE,
∵∠DOE=∠BOD,
∴∠AOF+∠BOD=∠FOE+∠DOE=×180°=90°,即∠FOD=90°,
∴OF与OD的位置关系是OF⊥OD;
(2)∵∠AOC:∠AOD=1:5,
∴∠AOC=×180°=30°,
∴∠BOD=∠AOC=∠EOD=30°,
∴∠AOE=120°,
∴∠EOF=∠AOE=60°.
17.(1)115°;(2)45°
18.(1);(2).
19.(1)的余角是,;的补角是,
(2),
20.(1)根据图形可得:∠AOC、∠EOF、∠BOD都是∠AOF的余角;
(2)∠AOC=∠EOF=∠BOD,∠COE=∠BOF,∠AOD=∠COB,∠AOF=∠DOE(只须写出不重复的三对即可).
(3)①对顶角相等,∠BOC=∠AOD=140°.
②∠EOF=x°,则∠AOD=5x°,
由∠EOF+∠DOE=90°,∠DOE+∠BOD=90°,
∴∠BOD=∠EOF=x°,又∠AOD+∠BOD=180°,
所以x+5x=180,
解得x=30,
即∠EOF=30°
21.140°
(同步练习)
一、单选题
1.如图,直线,相交于点,,,平分,给出下列结论:①当时,;②为的平分线;③若时,;④.其中正确的结论有( )
A.4个 B.3个 C.2个 D.1个
2.如图,直线AB、CD相交于点O,,若,则等于( )
A. B. C. D.
3.如图,直线、、相交于点,且,平分,若,则的度数为( )
A. B. C. D.无法确定
4.如图,直线AB、CD相交于点O.若,则的大小为( )
A. B. C. D.
5.已知各角的度数如图所示,则下列各题中的和分别是( ).
A. B. C. D.
6.如图,已知,则图中与相等的角有( )
A. B. C. D.
7.下列各图中,与是对顶角的是( )
A. B.
C. D.
8.如图,直线相交于点,若,则的度数是( )
A.30° B.40° C.60° D.150°
9.下列说法:①点动成线;②相等的角是对顶角;③同角的余角相等;④两点之间直线最短,其中正确的有( )
A.1个 B.2个 C.3个 D.4个
10.下图中,和是对顶角的是( )
A. B.
C. D.
二、填空题
11.如图直线AB,CD相交于O,直线FE⊥AB于O,∠BOD=75°,则∠COF的度数为_____度.
12.如图,直线、相交,若与互余,则的度数为____________.
13.如图,直线、、相交于点,若,则______
14.已知,直线AB和直线CD交于点O,∠BOD是它的邻补角的3倍,则直线AB与直线CD的夹角是________度.
15.如图,O是直线上一点,,则___.
三、解答题
16.如图,直线AB、CD相交于点O,∠DOE=∠BOD,OF平分∠AOE.
(1)判断OF与OD的位置关系,并说明理由;
(2)若∠AOC:∠AOD=1:5,求∠EOF的度数.
17.如图,直线AB,CD相交于点O,OF⊥CD,OE平分∠BOC.
(1)若∠BOE=65°,求∠DOE的度数;
(2)若∠BOD:∠BOE=2:3,求∠AOF的度数.
18.如图,直线、相交于点,平分,.
(1)若∠AOF=50°,求∠BOE的度数;
(2)若∠BOD:∠BOE=1:4,求∠AOF的度数.
19.如图,直线,,相交于点,平分,.
(1)写出的余角和补角;
(2)若,求和的度数.
20.如图,直线AB与CD相交于点O,OEAB,OFCD.
(1)图中∠AOF的余角是 (把符合条件的角都填出来).
(2)图中除直角相等外,还有相等的角,请写出三对:
① ;② ;③ .
(3)①如果∠AOD=140°.那么根据 ,可得∠BOC= 度.
②如果,求∠EOF的度数.
21.如图所示,直线a,b,c两两相交,,求的度数.
参考答案:
1.B2.C3.B4.C5.B6.D7.D8.A9.B10.B
11.15
12.
13.30
14.45
15.
16.(1)解:OF⊥OD,
理由:∵OF平分∠AOE,
∴∠AOF=∠FOE,
∵∠DOE=∠BOD,
∴∠AOF+∠BOD=∠FOE+∠DOE=×180°=90°,即∠FOD=90°,
∴OF与OD的位置关系是OF⊥OD;
(2)∵∠AOC:∠AOD=1:5,
∴∠AOC=×180°=30°,
∴∠BOD=∠AOC=∠EOD=30°,
∴∠AOE=120°,
∴∠EOF=∠AOE=60°.
17.(1)115°;(2)45°
18.(1);(2).
19.(1)的余角是,;的补角是,
(2),
20.(1)根据图形可得:∠AOC、∠EOF、∠BOD都是∠AOF的余角;
(2)∠AOC=∠EOF=∠BOD,∠COE=∠BOF,∠AOD=∠COB,∠AOF=∠DOE(只须写出不重复的三对即可).
(3)①对顶角相等,∠BOC=∠AOD=140°.
②∠EOF=x°,则∠AOD=5x°,
由∠EOF+∠DOE=90°,∠DOE+∠BOD=90°,
∴∠BOD=∠EOF=x°,又∠AOD+∠BOD=180°,
所以x+5x=180,
解得x=30,
即∠EOF=30°
21.140°
