2022-2023学年人教版九年级数学下册 第二十七章 相似形 单元自测题 (含解析)
文档属性
| 名称 | 2022-2023学年人教版九年级数学下册 第二十七章 相似形 单元自测题 (含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 786.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-06 16:08:08 | ||
图片预览




文档简介
人教版九年级数学下册 第二十七章 相似形 单元自测题
一、单选题
1.比值为(约0.618)的比例被公认为是最能引起美感的比例,因此被称为黄金分割比,我们中国的国旗宽与长之比就非常接近这个比例,如果某面国旗长为2米,则其宽约为( )
A.1.5米 B.1.2米 C.1.0米 D.0.8米
2.若,则的值是( )
A. B. C. D.
3.如图,两条直线被三条平行线所截,,则的长为( )
A.3.2 B.3.6 C.4 D.4.2
4.已知,则的值是( )
A. B. C. D.
5.如图示,已知,那么添加下列一个条件后,仍无法判定的是( )
A. B. C. D.
6.如图,一块等腰直角三角板,它的斜边BC=8cm,内部△DEF的各边与OABC的各边分别平行,且它的斜边EF=4cm,则△DEF的面积与阴影部分的面积比为( )
A.1:2 B.1:3 C.1:4 D.1:8
7.如图,,若,,则DF的长为( )
A.2 B.4 C.6 D.8
8.如图,在中,点D、E分别是、的中点,则下列四个结论,其中错误的结论是( )
A. B.
C. D.
9.如图,线段的两个端点坐标分别为A(2,2)、B(4,2),以原点O为位似中心, 将线段缩小后得到线段, 若,则端点E的坐标为( )
A.(1,1) B.(1,2) C.(2,1) D.(2,2)
10.三个顶点的坐标分别为,,,以原点O为位似中心,把这个三角形缩小为原来的,可以得到,则点的坐标是( )
A. B.或
C.或 D.
二、填空题
11.如果点是线段的黄金分割点,,则 .
12.已知且.若,则 .
13.如图,中,点D是中点,点E在上且,、交于点F,如果的面积为2,则的面积为 .
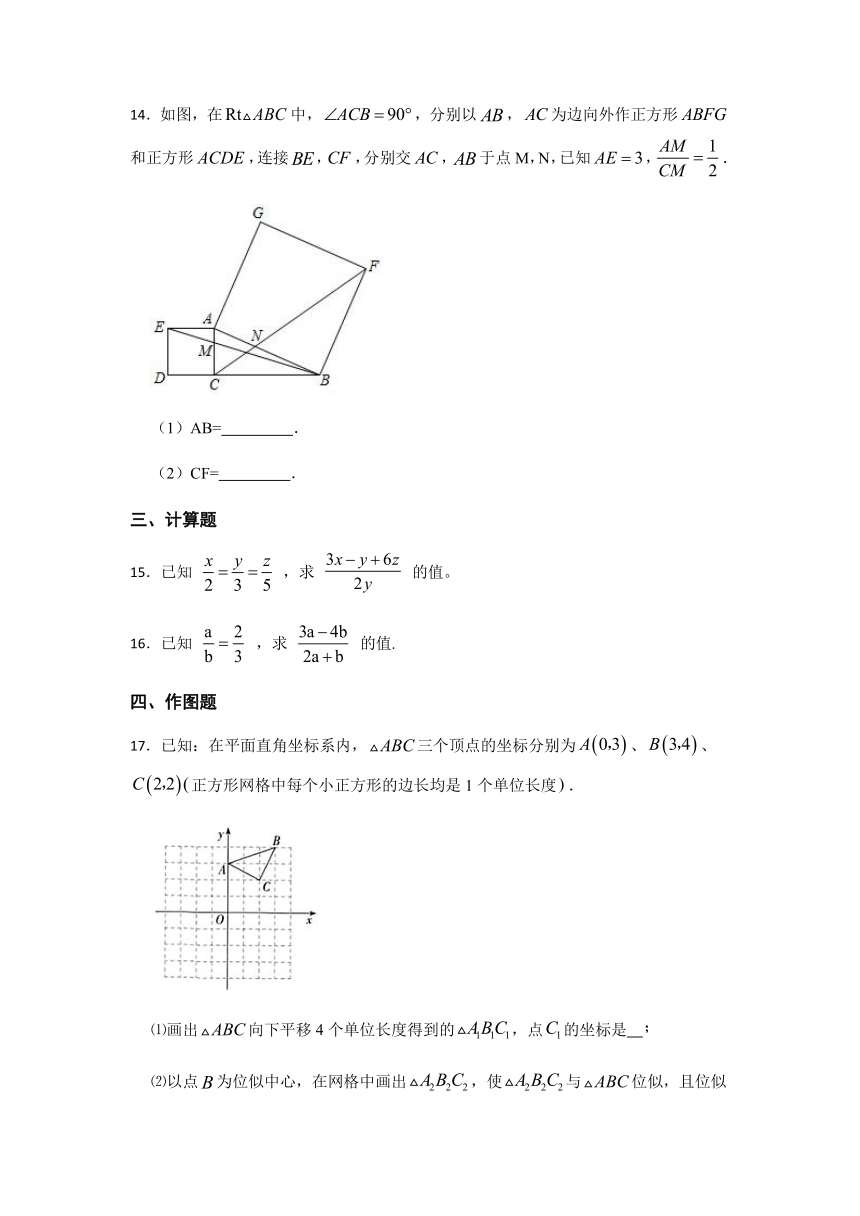
14.如图,在中,,分别以,为边向外作正方形和正方形,连接,,分别交,于点M,N,已知,.
(1)AB= .
(2)CF= .
三、计算题
15.已知 ,求 的值。
16.已知 ,求 的值.
四、作图题
17.已知:在平面直角坐标系内,三个顶点的坐标分别为、、正方形网格中每个小正方形的边长均是1个单位长度.
⑴画出向下平移4个单位长度得到的,点的坐标是
⑵以点为位似中心,在网格中画出,使与位似,且位似比为,点的坐标是
⑶求的面积.
五、解答题
18.如图,在中,,D是边上一点,.求证.
19.如图,,,,,.求的长度.
20.如图,已知,,垂足分别为B、C,交于点D,,,,求的长.
六、综合题
21.如图,在平面直角坐标系中,二次函数的图象与y轴交于点,与x轴交于B、C两点,其中点B的坐标是,点为该二次函数在第二象限内图象上的动点,点D为,连接.
(1)求该二次函数的表达式;
(2)依题补图1:连接,过点P作轴于点Q;当和相似时,求m的值;
(3)如图2,过点P作直线,和轴交点为Q,在点P沿着抛物线从点A到点B运动过程中,当与抛物线只有一个交点时,求点Q的坐标.
22.我国古代数学家赵爽利用影子对物体进行测量的方法,至今仍有借鉴意义.如图1,身高的小王晚上在路灯灯柱下散步,他想通过测量自己的影长来估计路灯的高度,具体做法如下:先从路灯底部A向东走20步到M处,发现自己的影子端点落在点P处,作好记号后,继续沿刚才自己的影子走4步恰好到达点P处,此时影子的端点在点Q处,已知小王和灯柱的底端在同一水平线上,小王的步间距保持一致.
(1)请在图中画出路灯O和影子端点Q的位置.
(2)估计路灯的高,并求影长的步数.
(3)无论点光源还是视线,其本质是相同的,日常生活中我们也可以直接利用视线解决问题.如图2,小明同学用自制的直角三角形纸板测量树的高度,他调整自己的位置,设法使斜边保持水平,并且边与点B在同一直线上.测得,,,小明眼睛到地面的距离为,则树高为 m.
23.
(1)【基础巩固】如图1,在中,E是上一点,过点E作的平行线交于点F,点D是上任意一点,连结交于点G,求证:;
(2)【尝试应用】
如图2,在(1)的条件下,连结,,若,、恰好将三等分,求的值;
(3)【拓展延伸】
如图3,在等边中,,连结,点E在上,若,求的值.
答案解析部分
1.【答案】B
【解析】【解答】解:设国旗的宽为x米,
由题意得x∶2=0.618,
解得x≈1.2.
故答案为:B.
【分析】根据中国的国旗宽与长之比等于黄金分割比例出方程,求解即可.
2.【答案】D
【解析】【解答】解:
即
故答案为:D.
【分析】根据比例的性质,两内项之积等于两外项之积,将等积式改写成比例式即可.
3.【答案】B
【解析】【解答】解:∵,
∴,
∵,
∴,,
∴,
∴.
故答案为:B.
【分析】根据平行线分线段成比例进行解答即可.
4.【答案】D
【解析】【解答】解:∵,
∴可设a=3k,b=2k,
∴,
故答案为:D.
【分析】根据比例的性质设a=3k,b=2k,进而代入所求式子再合并约分即可得出答案.
5.【答案】D
【解析】【解答】解:∵
∴
A、,两个三角形的对应角相等,那么,故A选项不符合题意;
B、,两个三角形的对应角相等,那么,故B选项不符合题意;
C、,两个三角形的两条对应边的比相等且夹角相等,那么,故C选项不符合题意;
D、,与的大小无法判断,即无法判定,故D选项符合题意.
故答案为:D.
【分析】由∠1=∠2可推出∠CAB=∠EAD,根据有两组角对应相等的两个三角形相似可以添加∠B=∠D或∠C=∠AED,根据两个三角形的两条对应边的比相等且夹角相等的三角形相似可以添加,从而一一判断得出答案.
6.【答案】B
【解析】【解答】解:由题可得:,
∴,
即 △DEF的面积与阴影部分的面积比为 1:3,
故答案为:B.
【分析】利用相似三角形的面积比等于相似比的平方求解即可。
7.【答案】D
【解析】【解答】解:∵,,,
∴,
∴,
∴DF=8,
故答案为:D.
【分析】根据题意先求出,再求出,最后计算求解即可。
8.【答案】D
【解析】【解答】解:∵在△ABC中,点D、E分别是AB、AC的中点,
∴DEBC,DE=BC,
∴;故A正确;
∵DE BC,
∴△DEO∽△CBO,
∴ ,,
∴,故B、C正确;
∵△DOE和△DOB同高,所以面积之比等于底之比,
∴,故D错误;
故答案为:D.
【分析】由题意可得DE为△ABC的中位线,则DE∥BC,DE=BC,据此判断A;易证△DEO∽△CBO,根据相似三角形的性质可判断B、C;根据同高的三角形面积之比等于对应底边的比可判断D.
9.【答案】C
【解析】【解答】解:将线段缩小后得到线段, 若,说明DE是原来的,位似比是,
∵D(1,1),
∴E的坐标是(2,1),
故答案为:C.
【分析】将点D的横坐标乘以2、纵坐标不变可得点E的坐标.
10.【答案】B
【解析】【解答】解:以原点O为位似中心,把缩小为原来的,得到,
∵点A的坐标为,
∴点的坐标为或,
即点坐标为或,
故答案为:B.
【分析】给点A的横、纵坐标分别乘以或-就可得到点A′的坐标.
11.【答案】
【解析】【解答】解:点是线段的黄金分割点,
,
故答案为:.
【分析】根据黄金分割的特点可得,据此解答.
12.【答案】
【解析】【解答】解:,
,
,
.
故答案为:.
【分析】由比例的性质可得,代入等式得,两边同除以2即得结论.
13.【答案】40
【解析】【解答】解:过D作 交于G.
∵D是的中点,
∴G是的中点,
∴.
∵,
∴设,
则.
∵,
∴,
∴ .
∵,
∴.
∵,
∴,
∴,
∴,
∴.
故答案为.
【分析】过D作DG∥AE交BC于G,则G为EC的中点,EG=GC,由已知条件可知EC=3BE,设BE=2x,则EG=GC=3x,证明△BEF∽△BGD,根据相似三角形的面积比等于相似比的平方可得S△BGD=12.5,根据等高的三角形面积之比等于对应底边的比可得S△BGD:S△DGC=BG:GC=5:3,则S△DGC=7.5,据此求解.
14.【答案】(1)
(2)
【解析】【解答】解:(1)如图,过点F作,交的延长线于点H,
四边形是正方形,
,,
,
,
,
,
故答案为:;
(2)四边形是正方形,
,,
,
,
在和中,
,
,
,,
,
,
故答案为:.
【分析】(1)过点F作,交的延长线于点H,先证出,可得,求出BC的长,再利用勾股定理求出AB的长即可;
(2)先利用“AAS”证出,可得,,利用线段的和差求出CH的长,最后利用勾股定理求出CF的长即可。
15.【答案】解:∵ ,∴可设x=2k,则y=3k,z=5k
∴
【解析】【分析】根据题意,可设x=2k,则y=3k,z=5,代入分式,即可求解.
16.【答案】解:∵ ,
∴a b,
∴ .
【解析】【分析】 由,可得a b,接着将a值代入式子中化简求值即得.
17.【答案】解:(1)如图所示, 即为所求;
;
点C1的坐标为(2,-2).
(2)如图所示, 即为所求;(1,0).
(3) , , ,
, ,
是等腰直角三角形,
的面积是 .
【解析】【分析】(1)利用方根纸的特点分别将点A、B、C向下平移4个单位长度得到其对应点A1、B1、C1,再连接A1B1、B1C1、C1A1即可,进而根据点C1的位置读出其坐标;
(2)利用方格纸的特点,延长BA至点A2,使AA2=AB,延长BC至点C2,使CC2=BC,再连接A2C2即可,进而根据点C2的位置读出其坐标即可;
(3)利用勾股定理算出A2C2、B2C2、A2B2,再根据勾股定理的逆定理判断出△A2B2C2是直角三角形,最后根据直角三角形的面积计算方法算出答案.
18.【答案】证明:∵,,
∴.
∴.
∵,
∴
【解析】【分析】根据已知条件可得,由图形可得∠A=∠A,然后根据相似三角形的判定定理进行证明.
19.【答案】解:,
,
,
,
,
,
,
.
【解析】【分析】先证明,可得,再将数据代入求出即可。
20.【答案】解:∵,,
∴,
∴,
∴,
∵,,,
∴,
解得:,经检验符合题意.
【解析】【分析】先证明,可得,再将数据代入求出CE的长即可。
21.【答案】(1)解:把,代入得,
,解得,
该二次函数的表达为;
(2)解:如图:
设,
由,分两种情况:
当时,,
,
,
即,解得,或(舍去);
当时,,
,
即,解或(舍去),
综上所述,m的值为或;
(3)解:如图,
设直线解析式为,
,解得,
直线解析式为,
,
设直线的解析式为,
当直线与的图象只有一个交点时,
联立,
整理得,
,
解得,
当时,直线的解析式为,
此时直线与的图象只有一个交点,
令,则,解得,
此时.
【解析】【分析】(1)将A(0,8)、B(-8,0)代入可求出b、c的值,据此可得二次函数的解析式;
(2)设P(m,m2-m+8),然后分△POQ∽△BDO、△POQ∽△DBO,根据相似三角形的性质可得PQ与OQ的关系,据此可求出m的值;
(3)利用待定系数法求出直线BD的解析式,根据两直线平行的条件可得直线PQ的解析式,联立二次函数的解析式并结合判别式为0可得n的值,得到直线PQ的解析式,然后令y=0,求出x的值,进而可得点Q的坐标.
22.【答案】(1)解:路灯O和影子端点Q的位置如图所示.
(2)解:∵,
∴,
∴,即,
解得.
∵,
∴,
∴,即,
解得,
∴路灯的高为,影长为步.
(3)9
【解析】【解答】(3)如图,∵,,,
∴,
∴,
∵,,
∴,
∵四边形是矩形,
∴,
∴,
故答案为:9.
【分析】(1)根据题意作出图象即可;
(2)先证出,可得,求出,再证出,可得,即,最后求出即可;
(3)根据,,求出,再利用线段的和差求出AB的长即可。
23.【答案】(1)证明:∵,
∴,
∴,
同理,
∴,
∴;
(2)解:∵,
∴,,
∵、恰好将三等分,
∴,
∴,
∵,
∴
在中,,
∴,
根据(1)得,;
(3)解:过E作的平行线,分别交、于G、H.
∵是等边三角形,
∴,,
∵,
∴
∴也是等边三角形,
∴,
∴,
∴,
又∵
∴
∴
∴.
∴,即,
∴,
由(1)和,得,
设,则.
∴,,
∴,
∴.
∵,
∴,
∵,
∴,
∴,
即,
∴,
∴.
【解析】【分析】(1)易证△AEG∽△ABD,根据相似三角形的性质可得,同理可得,则, 据此证明;
(2)根据平行线的性质可得∠C=∠AFE=30°,∠EFB=∠FBD,根据题意可得∠AFE=∠EFB=∠BFD=30°,则∠AFD=∠DFC=90°,进而推出DF=BD,根据含30°角的直角三角形的性质可得DF=DC,则,据此解答;
(3)过点E作BC的平行线,分别交AB、AC于点G、H,根据等边三角形的性质可得∠ABC=∠ACB=∠BAC=60°,AB=AC,由平行线的性质可得∠AGH=∠AHG=∠BAC=60°,推出△AGH为等边三角形,得到AG=AH,易证△GEB∽△HCE,根据相似三角形的性质可得GE·EH=BG2,由(1)和BD=4DC可得,设EH=a,则GE=4a,BG2=4a2,AG=GH=5a,BG=CH=2a,AC=BC=7a,证明△GEB∽△EBC,然后根据相似三角形的性质进行计算.
一、单选题
1.比值为(约0.618)的比例被公认为是最能引起美感的比例,因此被称为黄金分割比,我们中国的国旗宽与长之比就非常接近这个比例,如果某面国旗长为2米,则其宽约为( )
A.1.5米 B.1.2米 C.1.0米 D.0.8米
2.若,则的值是( )
A. B. C. D.
3.如图,两条直线被三条平行线所截,,则的长为( )
A.3.2 B.3.6 C.4 D.4.2
4.已知,则的值是( )
A. B. C. D.
5.如图示,已知,那么添加下列一个条件后,仍无法判定的是( )
A. B. C. D.
6.如图,一块等腰直角三角板,它的斜边BC=8cm,内部△DEF的各边与OABC的各边分别平行,且它的斜边EF=4cm,则△DEF的面积与阴影部分的面积比为( )
A.1:2 B.1:3 C.1:4 D.1:8
7.如图,,若,,则DF的长为( )
A.2 B.4 C.6 D.8
8.如图,在中,点D、E分别是、的中点,则下列四个结论,其中错误的结论是( )
A. B.
C. D.
9.如图,线段的两个端点坐标分别为A(2,2)、B(4,2),以原点O为位似中心, 将线段缩小后得到线段, 若,则端点E的坐标为( )
A.(1,1) B.(1,2) C.(2,1) D.(2,2)
10.三个顶点的坐标分别为,,,以原点O为位似中心,把这个三角形缩小为原来的,可以得到,则点的坐标是( )
A. B.或
C.或 D.
二、填空题
11.如果点是线段的黄金分割点,,则 .
12.已知且.若,则 .
13.如图,中,点D是中点,点E在上且,、交于点F,如果的面积为2,则的面积为 .
14.如图,在中,,分别以,为边向外作正方形和正方形,连接,,分别交,于点M,N,已知,.
(1)AB= .
(2)CF= .
三、计算题
15.已知 ,求 的值。
16.已知 ,求 的值.
四、作图题
17.已知:在平面直角坐标系内,三个顶点的坐标分别为、、正方形网格中每个小正方形的边长均是1个单位长度.
⑴画出向下平移4个单位长度得到的,点的坐标是
⑵以点为位似中心,在网格中画出,使与位似,且位似比为,点的坐标是
⑶求的面积.
五、解答题
18.如图,在中,,D是边上一点,.求证.
19.如图,,,,,.求的长度.
20.如图,已知,,垂足分别为B、C,交于点D,,,,求的长.
六、综合题
21.如图,在平面直角坐标系中,二次函数的图象与y轴交于点,与x轴交于B、C两点,其中点B的坐标是,点为该二次函数在第二象限内图象上的动点,点D为,连接.
(1)求该二次函数的表达式;
(2)依题补图1:连接,过点P作轴于点Q;当和相似时,求m的值;
(3)如图2,过点P作直线,和轴交点为Q,在点P沿着抛物线从点A到点B运动过程中,当与抛物线只有一个交点时,求点Q的坐标.
22.我国古代数学家赵爽利用影子对物体进行测量的方法,至今仍有借鉴意义.如图1,身高的小王晚上在路灯灯柱下散步,他想通过测量自己的影长来估计路灯的高度,具体做法如下:先从路灯底部A向东走20步到M处,发现自己的影子端点落在点P处,作好记号后,继续沿刚才自己的影子走4步恰好到达点P处,此时影子的端点在点Q处,已知小王和灯柱的底端在同一水平线上,小王的步间距保持一致.
(1)请在图中画出路灯O和影子端点Q的位置.
(2)估计路灯的高,并求影长的步数.
(3)无论点光源还是视线,其本质是相同的,日常生活中我们也可以直接利用视线解决问题.如图2,小明同学用自制的直角三角形纸板测量树的高度,他调整自己的位置,设法使斜边保持水平,并且边与点B在同一直线上.测得,,,小明眼睛到地面的距离为,则树高为 m.
23.
(1)【基础巩固】如图1,在中,E是上一点,过点E作的平行线交于点F,点D是上任意一点,连结交于点G,求证:;
(2)【尝试应用】
如图2,在(1)的条件下,连结,,若,、恰好将三等分,求的值;
(3)【拓展延伸】
如图3,在等边中,,连结,点E在上,若,求的值.
答案解析部分
1.【答案】B
【解析】【解答】解:设国旗的宽为x米,
由题意得x∶2=0.618,
解得x≈1.2.
故答案为:B.
【分析】根据中国的国旗宽与长之比等于黄金分割比例出方程,求解即可.
2.【答案】D
【解析】【解答】解:
即
故答案为:D.
【分析】根据比例的性质,两内项之积等于两外项之积,将等积式改写成比例式即可.
3.【答案】B
【解析】【解答】解:∵,
∴,
∵,
∴,,
∴,
∴.
故答案为:B.
【分析】根据平行线分线段成比例进行解答即可.
4.【答案】D
【解析】【解答】解:∵,
∴可设a=3k,b=2k,
∴,
故答案为:D.
【分析】根据比例的性质设a=3k,b=2k,进而代入所求式子再合并约分即可得出答案.
5.【答案】D
【解析】【解答】解:∵
∴
A、,两个三角形的对应角相等,那么,故A选项不符合题意;
B、,两个三角形的对应角相等,那么,故B选项不符合题意;
C、,两个三角形的两条对应边的比相等且夹角相等,那么,故C选项不符合题意;
D、,与的大小无法判断,即无法判定,故D选项符合题意.
故答案为:D.
【分析】由∠1=∠2可推出∠CAB=∠EAD,根据有两组角对应相等的两个三角形相似可以添加∠B=∠D或∠C=∠AED,根据两个三角形的两条对应边的比相等且夹角相等的三角形相似可以添加,从而一一判断得出答案.
6.【答案】B
【解析】【解答】解:由题可得:,
∴,
即 △DEF的面积与阴影部分的面积比为 1:3,
故答案为:B.
【分析】利用相似三角形的面积比等于相似比的平方求解即可。
7.【答案】D
【解析】【解答】解:∵,,,
∴,
∴,
∴DF=8,
故答案为:D.
【分析】根据题意先求出,再求出,最后计算求解即可。
8.【答案】D
【解析】【解答】解:∵在△ABC中,点D、E分别是AB、AC的中点,
∴DEBC,DE=BC,
∴;故A正确;
∵DE BC,
∴△DEO∽△CBO,
∴ ,,
∴,故B、C正确;
∵△DOE和△DOB同高,所以面积之比等于底之比,
∴,故D错误;
故答案为:D.
【分析】由题意可得DE为△ABC的中位线,则DE∥BC,DE=BC,据此判断A;易证△DEO∽△CBO,根据相似三角形的性质可判断B、C;根据同高的三角形面积之比等于对应底边的比可判断D.
9.【答案】C
【解析】【解答】解:将线段缩小后得到线段, 若,说明DE是原来的,位似比是,
∵D(1,1),
∴E的坐标是(2,1),
故答案为:C.
【分析】将点D的横坐标乘以2、纵坐标不变可得点E的坐标.
10.【答案】B
【解析】【解答】解:以原点O为位似中心,把缩小为原来的,得到,
∵点A的坐标为,
∴点的坐标为或,
即点坐标为或,
故答案为:B.
【分析】给点A的横、纵坐标分别乘以或-就可得到点A′的坐标.
11.【答案】
【解析】【解答】解:点是线段的黄金分割点,
,
故答案为:.
【分析】根据黄金分割的特点可得,据此解答.
12.【答案】
【解析】【解答】解:,
,
,
.
故答案为:.
【分析】由比例的性质可得,代入等式得,两边同除以2即得结论.
13.【答案】40
【解析】【解答】解:过D作 交于G.
∵D是的中点,
∴G是的中点,
∴.
∵,
∴设,
则.
∵,
∴,
∴ .
∵,
∴.
∵,
∴,
∴,
∴,
∴.
故答案为.
【分析】过D作DG∥AE交BC于G,则G为EC的中点,EG=GC,由已知条件可知EC=3BE,设BE=2x,则EG=GC=3x,证明△BEF∽△BGD,根据相似三角形的面积比等于相似比的平方可得S△BGD=12.5,根据等高的三角形面积之比等于对应底边的比可得S△BGD:S△DGC=BG:GC=5:3,则S△DGC=7.5,据此求解.
14.【答案】(1)
(2)
【解析】【解答】解:(1)如图,过点F作,交的延长线于点H,
四边形是正方形,
,,
,
,
,
,
故答案为:;
(2)四边形是正方形,
,,
,
,
在和中,
,
,
,,
,
,
故答案为:.
【分析】(1)过点F作,交的延长线于点H,先证出,可得,求出BC的长,再利用勾股定理求出AB的长即可;
(2)先利用“AAS”证出,可得,,利用线段的和差求出CH的长,最后利用勾股定理求出CF的长即可。
15.【答案】解:∵ ,∴可设x=2k,则y=3k,z=5k
∴
【解析】【分析】根据题意,可设x=2k,则y=3k,z=5,代入分式,即可求解.
16.【答案】解:∵ ,
∴a b,
∴ .
【解析】【分析】 由,可得a b,接着将a值代入式子中化简求值即得.
17.【答案】解:(1)如图所示, 即为所求;
;
点C1的坐标为(2,-2).
(2)如图所示, 即为所求;(1,0).
(3) , , ,
, ,
是等腰直角三角形,
的面积是 .
【解析】【分析】(1)利用方根纸的特点分别将点A、B、C向下平移4个单位长度得到其对应点A1、B1、C1,再连接A1B1、B1C1、C1A1即可,进而根据点C1的位置读出其坐标;
(2)利用方格纸的特点,延长BA至点A2,使AA2=AB,延长BC至点C2,使CC2=BC,再连接A2C2即可,进而根据点C2的位置读出其坐标即可;
(3)利用勾股定理算出A2C2、B2C2、A2B2,再根据勾股定理的逆定理判断出△A2B2C2是直角三角形,最后根据直角三角形的面积计算方法算出答案.
18.【答案】证明:∵,,
∴.
∴.
∵,
∴
【解析】【分析】根据已知条件可得,由图形可得∠A=∠A,然后根据相似三角形的判定定理进行证明.
19.【答案】解:,
,
,
,
,
,
,
.
【解析】【分析】先证明,可得,再将数据代入求出即可。
20.【答案】解:∵,,
∴,
∴,
∴,
∵,,,
∴,
解得:,经检验符合题意.
【解析】【分析】先证明,可得,再将数据代入求出CE的长即可。
21.【答案】(1)解:把,代入得,
,解得,
该二次函数的表达为;
(2)解:如图:
设,
由,分两种情况:
当时,,
,
,
即,解得,或(舍去);
当时,,
,
即,解或(舍去),
综上所述,m的值为或;
(3)解:如图,
设直线解析式为,
,解得,
直线解析式为,
,
设直线的解析式为,
当直线与的图象只有一个交点时,
联立,
整理得,
,
解得,
当时,直线的解析式为,
此时直线与的图象只有一个交点,
令,则,解得,
此时.
【解析】【分析】(1)将A(0,8)、B(-8,0)代入可求出b、c的值,据此可得二次函数的解析式;
(2)设P(m,m2-m+8),然后分△POQ∽△BDO、△POQ∽△DBO,根据相似三角形的性质可得PQ与OQ的关系,据此可求出m的值;
(3)利用待定系数法求出直线BD的解析式,根据两直线平行的条件可得直线PQ的解析式,联立二次函数的解析式并结合判别式为0可得n的值,得到直线PQ的解析式,然后令y=0,求出x的值,进而可得点Q的坐标.
22.【答案】(1)解:路灯O和影子端点Q的位置如图所示.
(2)解:∵,
∴,
∴,即,
解得.
∵,
∴,
∴,即,
解得,
∴路灯的高为,影长为步.
(3)9
【解析】【解答】(3)如图,∵,,,
∴,
∴,
∵,,
∴,
∵四边形是矩形,
∴,
∴,
故答案为:9.
【分析】(1)根据题意作出图象即可;
(2)先证出,可得,求出,再证出,可得,即,最后求出即可;
(3)根据,,求出,再利用线段的和差求出AB的长即可。
23.【答案】(1)证明:∵,
∴,
∴,
同理,
∴,
∴;
(2)解:∵,
∴,,
∵、恰好将三等分,
∴,
∴,
∵,
∴
在中,,
∴,
根据(1)得,;
(3)解:过E作的平行线,分别交、于G、H.
∵是等边三角形,
∴,,
∵,
∴
∴也是等边三角形,
∴,
∴,
∴,
又∵
∴
∴
∴.
∴,即,
∴,
由(1)和,得,
设,则.
∴,,
∴,
∴.
∵,
∴,
∵,
∴,
∴,
即,
∴,
∴.
【解析】【分析】(1)易证△AEG∽△ABD,根据相似三角形的性质可得,同理可得,则, 据此证明;
(2)根据平行线的性质可得∠C=∠AFE=30°,∠EFB=∠FBD,根据题意可得∠AFE=∠EFB=∠BFD=30°,则∠AFD=∠DFC=90°,进而推出DF=BD,根据含30°角的直角三角形的性质可得DF=DC,则,据此解答;
(3)过点E作BC的平行线,分别交AB、AC于点G、H,根据等边三角形的性质可得∠ABC=∠ACB=∠BAC=60°,AB=AC,由平行线的性质可得∠AGH=∠AHG=∠BAC=60°,推出△AGH为等边三角形,得到AG=AH,易证△GEB∽△HCE,根据相似三角形的性质可得GE·EH=BG2,由(1)和BD=4DC可得,设EH=a,则GE=4a,BG2=4a2,AG=GH=5a,BG=CH=2a,AC=BC=7a,证明△GEB∽△EBC,然后根据相似三角形的性质进行计算.
