5.2平行线及其判定 同步练习 (含答案)2022-2023学年人教版数学七年级下册
文档属性
| 名称 | 5.2平行线及其判定 同步练习 (含答案)2022-2023学年人教版数学七年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 583.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-06 16:57:53 | ||
图片预览




文档简介
5.2平行线及其判定
(同步练习)
一、单选题
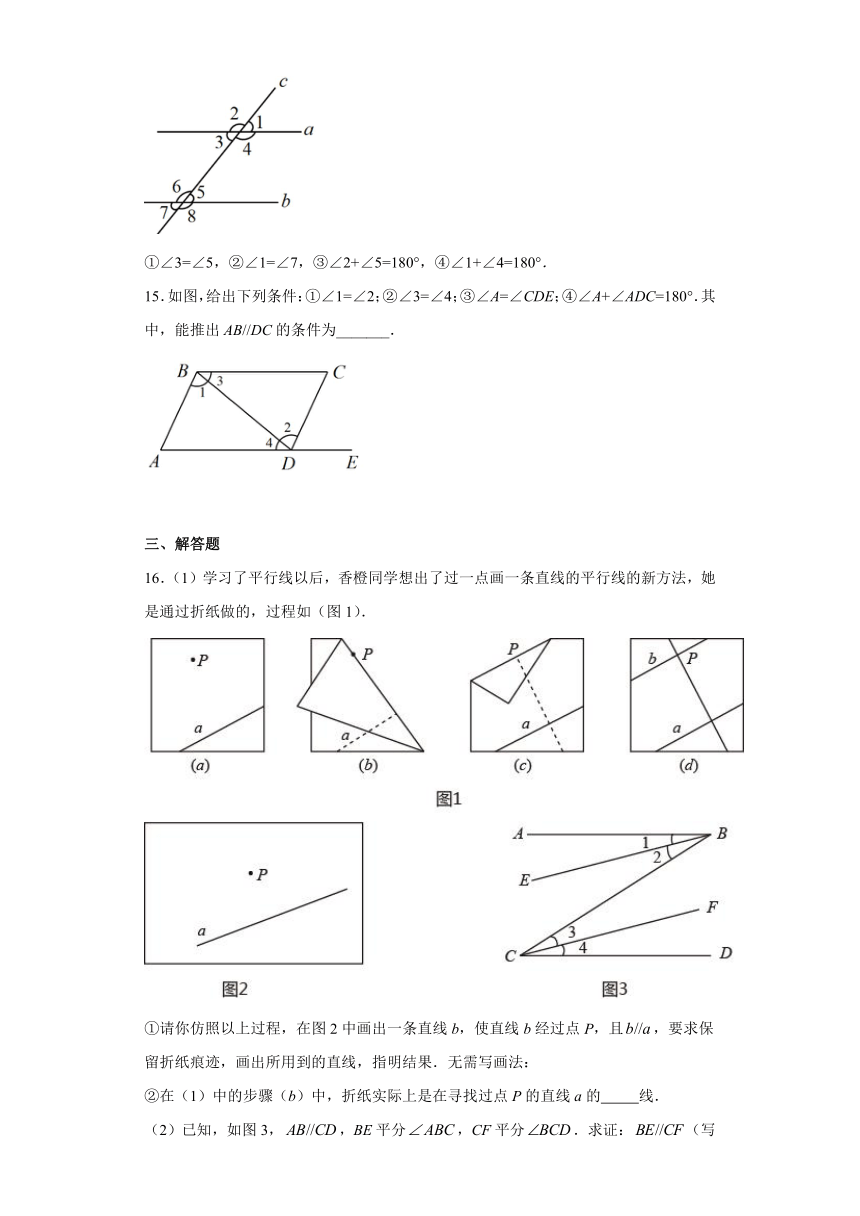
1.如图,下列说法中,正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
2.在同一平面内,两条直线的位置关系可能是( )
A.相交或垂直 B.垂直或平行
C.平行或相交 D.相交或垂直或平行
3.下列说法中是真命题正确的个数有( )个
(1)若ab,bd,则ad;(2)过一点有且只有一条直线与已知直线平行;(3)两条直线不相交就平行;(4)过一点有且只有一条直线与已知直线垂直.
A.1个 B.2个 C.3个 D.4个
4.给出下列说法:
(1)过直线外一点有且只有一条直线与已知直线平行;
(2)相等的两个角是对顶角;
(3)直线外一点到这条直线的垂线段,叫做这点到直线的距离;
(4)垂直于同一条直线的两直线平行;其中正确的有( )
A.0个 B.1个 C.2个 D.3个
5.图所示,点E在的延长线上,下列条件中不能判断的是( ).
B.
C. D.
6.如图,直线,被所截得的同旁内角为,,要使,只要使( )
A. B.
C. D.,
7.如图,在下列四组条件中,能判断的是( )
B.
C. D.
8.下列说法正确的是( )
A.直线外一点到已知直线的垂线段叫做这点到直线的距离.
B.过直线外一点有且只有一条直线与已知直线平行.
C.三角形的三条高线交于一点.
D.平面内,有且只有一条直线与已知直线垂直.
9.如图,下面哪个条件不能判断的是( )
A. B.
C. D.
10.如图,如果,那么,其依据可以简单说成( )
A.两直线平行,内错角相等 B.内错角相等,两直线平行
C.两直线平行,同位角相等 D.同位角相等,两直线平行
二、填空题
11.如图,不添加辅助线,请写出一个能判定ABCD的条件__
12.在数学课上,老师要求同学们利用一副三角板任作两条平行线.小明的作法如下:
如图,(1)任取两点A,B,画直线.
(2)分别过点A,B作直线的两条垂线;
则直线即为所求.
老师说:“小明的作法正确.”请回答:小明的作图依据是________________________.
13.如图,把三角尺的直角顶点放在直线b上.若∠1= 50°,则当∠2=____时,ab.
14.如图,下列条件中能推出的有_______.
①∠3=∠5,②∠1=∠7,③∠2+∠5=180°,④∠1+∠4=180°.
15.如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠A=∠CDE;④∠A+∠ADC=180°.其中,能推出AB//DC的条件为_______.
三、解答题
16.(1)学行线以后,香橙同学想出了过一点画一条直线的平行线的新方法,她是通过折纸做的,过程如(图1).
①请你仿照以上过程,在图2中画出一条直线b,使直线b经过点P,且,要求保留折纸痕迹,画出所用到的直线,指明结果.无需写画法:
②在(1)中的步骤(b)中,折纸实际上是在寻找过点P的直线a的 线.
(2)已知,如图3,,BE平分,CF平分.求证:(写出每步的依据).
17.在△ABC中,∠C=90°,AM平分∠BAC,D为直线BC上一点,DE⊥AB于点E,∠CDE的平分线交直线AC于点F.
(1)如图①,当点D在边BC上时,判断DF与AM的位置关系,并说明理由;
(2)①如图②,当点D在边BC延长线上时,则DF与AM的位置关系是______;
②如图③,当点D在边CB延长线上时,则DF与AM的位置关系是______;
(3)请就(2)中①或②中的一种情况,给出证明.
18.按以下各步画图(不写画法)
(1)画出一个角∠MON,且使∠MON=150°;
(2)在角∠MON内任取一点P,过点P作 ,交射线OM于点A;
(3)过点A作垂线AB,使AB⊥ON,垂足为点B;
(4)画射线PO(或反向延长射线PO)交垂线AB于点C
19.按逻辑填写步骤和理由,将下面的证明过程补充完整
如图,直线MN分别与直线AC、DG交于点B、F,且∠1=∠2.∠ABF的角平分线BE交直线DG于点E,∠BFG的角平分线FC交直线AC于点C.
求证:.
证明:∵∠1=∠2(已知)
∠ABF=∠1(对顶角相等)
∠BFG=∠2(____________)
∴∠ABF=______(等量代换)
∵BE平分∠ABF(已知)
∴______(____________)
∵FC平分∠BFG(已知)
∴______(____________)
∴∠EBF=______
∴(____________)
20.如图,点在上,已知,平分,平分.请说明的理由.
解:因为(已知),
(______),
所以(______).
因为平分,
所以(______).
因为平分,
所以______,
得(等量代换),
所以______(______).
21.(1)在一次数学活动课上,老师让同学们用两个大小、形状都相同的三角板画平行线、,并说出自己做法的依据.小琛、小萱、小冉三位同学的做法如下:
小琛说:“我的做法的依据是内错角相等,两直线平行”
①小琛说的是否正确?________(回答正确或错误)
②小萱做法的依据是________________________;
③小冉做法的依据是________________________.
(2)如图,如果,,,那么与平行吗?与呢?
参考答案:
1.D2.C3.A4.B5.B6.C7.B8.B9.C10.D
11.∠1=∠4或∠B=∠5或∠B+∠BCD=180°.
12.在同一平面上,垂直于同一直线的两直线平行
13.40°
14.①②③
15.①③④
16.(1)解:①如图2所示:
②在(1)中的步骤(b)中,折纸实际上是在寻找过点的直线的垂线.
故答案为垂;
(2)证明:平分,平分(已知),
,(角平分线的定义),
(已知),
(两直线平行,内错角相等),
(等量代换),
(等式性质),
(内错角相等,两直线平行).
17.(1)解:(1)DF//AM.理由如下:
∵∠C=90°,DE⊥AB,
∴∠BAC+∠CDE=360°﹣90°×2=180°,
∵AM平分∠BAC,DF平分∠CDE,
∴∠CAM=∠BAC,∠CDF=∠CDE,
∴∠CAM+∠CDF=(∠BAC+∠CDE)=90°,
又∵∠CAM+∠CMA=90°,
∴∠CDF=∠CMA,
∴BD//MF.
(2)①∵∠C=90°,DE⊥AB,
∴∠BAC+∠B=∠BDE+∠B=90°,
∴∠BAC=∠CDE,
∵AM平分∠BAC,DF平分∠CDE,
∴∠CAM=∠CDF,
∵∠CAM+∠AMC=90°,
∴∠CDF+∠AMC=90°,
∴DF⊥AM.
故答案为DF⊥AM.
②∵∠C=90°,DE⊥AB,
∴∠BAC+∠B=∠BDE+∠B=90°,
∴∠BAC=∠CDE,
∵AM平分∠BAC,DF平分∠CDE,
∴∠CAM=∠CDF,
∵∠CDF+∠F=90°,
∴∠CAM+∠F=90°,
∴DF⊥AM.
故答案为DF⊥AM.
(3)解:选②证明. 证明如下:
∵∠C=90°,DE⊥AB,
∴∠BAC+∠B=∠BDE+∠B=90°,
∴∠BAC=∠CDE,
∵AM平分∠BAC,DF平分∠CDE,
∴∠CAM=∠CDF,
∵∠CDF+∠F=90°,
∴∠CAM+∠F=90°,
∴DF⊥AM.
18.(1)如图,∠MON即为所求;
(2)如图,直线AP即为所求;
(3)如图,垂线AB即为所求;
(4)如图,射线PO,点C即为所求.
19.对顶角相等;∠BFG;∠ABF;角平分线的定义;∠BFG;角平分线的定义;∠CFB;内错角相等,两直线平行;
20.平角的定义;同角的补角相等;角平分线的定义;∠AGC;;内错角相等,两直线平行
21.(1)①正确;②同位角相等两直线平行;③同一平面内垂直于同一直线的两条直线平行;
(2)AB∥CD,BC∥DE;
(同步练习)
一、单选题
1.如图,下列说法中,正确的是( )
A.若,则 B.若,则
C.若,则 D.若,则
2.在同一平面内,两条直线的位置关系可能是( )
A.相交或垂直 B.垂直或平行
C.平行或相交 D.相交或垂直或平行
3.下列说法中是真命题正确的个数有( )个
(1)若ab,bd,则ad;(2)过一点有且只有一条直线与已知直线平行;(3)两条直线不相交就平行;(4)过一点有且只有一条直线与已知直线垂直.
A.1个 B.2个 C.3个 D.4个
4.给出下列说法:
(1)过直线外一点有且只有一条直线与已知直线平行;
(2)相等的两个角是对顶角;
(3)直线外一点到这条直线的垂线段,叫做这点到直线的距离;
(4)垂直于同一条直线的两直线平行;其中正确的有( )
A.0个 B.1个 C.2个 D.3个
5.图所示,点E在的延长线上,下列条件中不能判断的是( ).
B.
C. D.
6.如图,直线,被所截得的同旁内角为,,要使,只要使( )
A. B.
C. D.,
7.如图,在下列四组条件中,能判断的是( )
B.
C. D.
8.下列说法正确的是( )
A.直线外一点到已知直线的垂线段叫做这点到直线的距离.
B.过直线外一点有且只有一条直线与已知直线平行.
C.三角形的三条高线交于一点.
D.平面内,有且只有一条直线与已知直线垂直.
9.如图,下面哪个条件不能判断的是( )
A. B.
C. D.
10.如图,如果,那么,其依据可以简单说成( )
A.两直线平行,内错角相等 B.内错角相等,两直线平行
C.两直线平行,同位角相等 D.同位角相等,两直线平行
二、填空题
11.如图,不添加辅助线,请写出一个能判定ABCD的条件__
12.在数学课上,老师要求同学们利用一副三角板任作两条平行线.小明的作法如下:
如图,(1)任取两点A,B,画直线.
(2)分别过点A,B作直线的两条垂线;
则直线即为所求.
老师说:“小明的作法正确.”请回答:小明的作图依据是________________________.
13.如图,把三角尺的直角顶点放在直线b上.若∠1= 50°,则当∠2=____时,ab.
14.如图,下列条件中能推出的有_______.
①∠3=∠5,②∠1=∠7,③∠2+∠5=180°,④∠1+∠4=180°.
15.如图,给出下列条件:①∠1=∠2;②∠3=∠4;③∠A=∠CDE;④∠A+∠ADC=180°.其中,能推出AB//DC的条件为_______.
三、解答题
16.(1)学行线以后,香橙同学想出了过一点画一条直线的平行线的新方法,她是通过折纸做的,过程如(图1).
①请你仿照以上过程,在图2中画出一条直线b,使直线b经过点P,且,要求保留折纸痕迹,画出所用到的直线,指明结果.无需写画法:
②在(1)中的步骤(b)中,折纸实际上是在寻找过点P的直线a的 线.
(2)已知,如图3,,BE平分,CF平分.求证:(写出每步的依据).
17.在△ABC中,∠C=90°,AM平分∠BAC,D为直线BC上一点,DE⊥AB于点E,∠CDE的平分线交直线AC于点F.
(1)如图①,当点D在边BC上时,判断DF与AM的位置关系,并说明理由;
(2)①如图②,当点D在边BC延长线上时,则DF与AM的位置关系是______;
②如图③,当点D在边CB延长线上时,则DF与AM的位置关系是______;
(3)请就(2)中①或②中的一种情况,给出证明.
18.按以下各步画图(不写画法)
(1)画出一个角∠MON,且使∠MON=150°;
(2)在角∠MON内任取一点P,过点P作 ,交射线OM于点A;
(3)过点A作垂线AB,使AB⊥ON,垂足为点B;
(4)画射线PO(或反向延长射线PO)交垂线AB于点C
19.按逻辑填写步骤和理由,将下面的证明过程补充完整
如图,直线MN分别与直线AC、DG交于点B、F,且∠1=∠2.∠ABF的角平分线BE交直线DG于点E,∠BFG的角平分线FC交直线AC于点C.
求证:.
证明:∵∠1=∠2(已知)
∠ABF=∠1(对顶角相等)
∠BFG=∠2(____________)
∴∠ABF=______(等量代换)
∵BE平分∠ABF(已知)
∴______(____________)
∵FC平分∠BFG(已知)
∴______(____________)
∴∠EBF=______
∴(____________)
20.如图,点在上,已知,平分,平分.请说明的理由.
解:因为(已知),
(______),
所以(______).
因为平分,
所以(______).
因为平分,
所以______,
得(等量代换),
所以______(______).
21.(1)在一次数学活动课上,老师让同学们用两个大小、形状都相同的三角板画平行线、,并说出自己做法的依据.小琛、小萱、小冉三位同学的做法如下:
小琛说:“我的做法的依据是内错角相等,两直线平行”
①小琛说的是否正确?________(回答正确或错误)
②小萱做法的依据是________________________;
③小冉做法的依据是________________________.
(2)如图,如果,,,那么与平行吗?与呢?
参考答案:
1.D2.C3.A4.B5.B6.C7.B8.B9.C10.D
11.∠1=∠4或∠B=∠5或∠B+∠BCD=180°.
12.在同一平面上,垂直于同一直线的两直线平行
13.40°
14.①②③
15.①③④
16.(1)解:①如图2所示:
②在(1)中的步骤(b)中,折纸实际上是在寻找过点的直线的垂线.
故答案为垂;
(2)证明:平分,平分(已知),
,(角平分线的定义),
(已知),
(两直线平行,内错角相等),
(等量代换),
(等式性质),
(内错角相等,两直线平行).
17.(1)解:(1)DF//AM.理由如下:
∵∠C=90°,DE⊥AB,
∴∠BAC+∠CDE=360°﹣90°×2=180°,
∵AM平分∠BAC,DF平分∠CDE,
∴∠CAM=∠BAC,∠CDF=∠CDE,
∴∠CAM+∠CDF=(∠BAC+∠CDE)=90°,
又∵∠CAM+∠CMA=90°,
∴∠CDF=∠CMA,
∴BD//MF.
(2)①∵∠C=90°,DE⊥AB,
∴∠BAC+∠B=∠BDE+∠B=90°,
∴∠BAC=∠CDE,
∵AM平分∠BAC,DF平分∠CDE,
∴∠CAM=∠CDF,
∵∠CAM+∠AMC=90°,
∴∠CDF+∠AMC=90°,
∴DF⊥AM.
故答案为DF⊥AM.
②∵∠C=90°,DE⊥AB,
∴∠BAC+∠B=∠BDE+∠B=90°,
∴∠BAC=∠CDE,
∵AM平分∠BAC,DF平分∠CDE,
∴∠CAM=∠CDF,
∵∠CDF+∠F=90°,
∴∠CAM+∠F=90°,
∴DF⊥AM.
故答案为DF⊥AM.
(3)解:选②证明. 证明如下:
∵∠C=90°,DE⊥AB,
∴∠BAC+∠B=∠BDE+∠B=90°,
∴∠BAC=∠CDE,
∵AM平分∠BAC,DF平分∠CDE,
∴∠CAM=∠CDF,
∵∠CDF+∠F=90°,
∴∠CAM+∠F=90°,
∴DF⊥AM.
18.(1)如图,∠MON即为所求;
(2)如图,直线AP即为所求;
(3)如图,垂线AB即为所求;
(4)如图,射线PO,点C即为所求.
19.对顶角相等;∠BFG;∠ABF;角平分线的定义;∠BFG;角平分线的定义;∠CFB;内错角相等,两直线平行;
20.平角的定义;同角的补角相等;角平分线的定义;∠AGC;;内错角相等,两直线平行
21.(1)①正确;②同位角相等两直线平行;③同一平面内垂直于同一直线的两条直线平行;
(2)AB∥CD,BC∥DE;
