第二十章 数据的分析 单元自测题(含解析)2022-2023学年人教版八年级数学下册
文档属性
| 名称 | 第二十章 数据的分析 单元自测题(含解析)2022-2023学年人教版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 389.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-06 17:06:27 | ||
图片预览


文档简介
人教版八年级数学下册第二十章 数据的分析 单元自测题
一、单选题
1.下列命题是真命题的是( )
A.同位角相等
B.不是整式
C.数据6,3,10的中位数是3
D.第七次全国人口普查是全面调查
2.某校男子篮球队10名队员进行定点投篮练习,每人投篮10次,将他们投中的次数进行统计制成下表:则这10名队员投中的次数组成的一组数据中,众数和中位数分别为( )
投中次数 3 5 6 7 8 9
人数 1 3 2 2 1 1
A.5,6 B.2,6 C.5,5 D.6,5
3.某次数学测验中,八(1)班55人平均分为80分,八(2)班45人平均分为70分,则这两个班总平均分为( )
A.75分 B.75.5分 C.76分 D.76.5分
4.若一组数据的中位数为3,则的值为( )
A.1 B.2 C.3 D.4
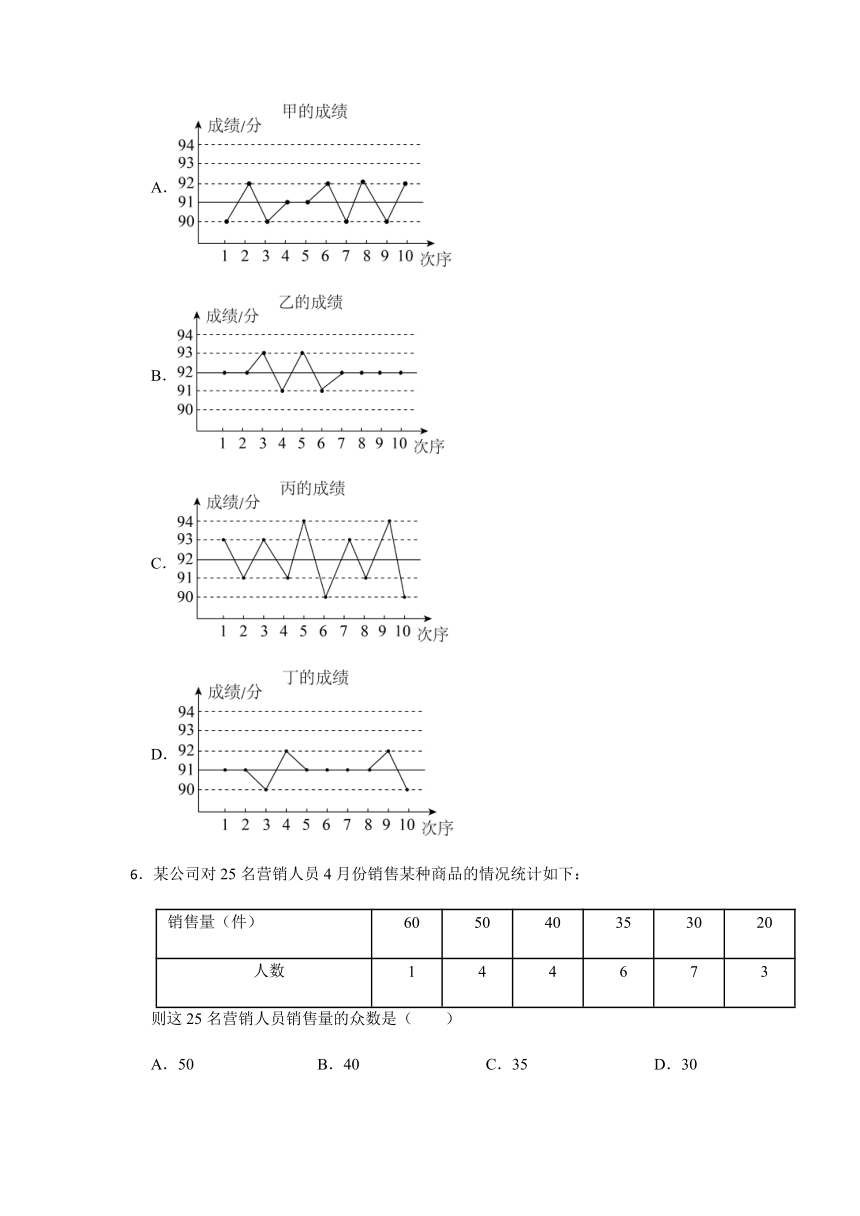
5.甲、乙、丙、丁四人10次随堂测验的成绩如图所示,从图中可以看出这10次测验平均成绩较高且较稳定的是( )
A.
B.
C.
D.
6.某公司对25名营销人员4月份销售某种商品的情况统计如下:
销售量(件) 60 50 40 35 30 20
人数 1 4 4 6 7 3
则这25名营销人员销售量的众数是( )
A.50 B.40 C.35 D.30
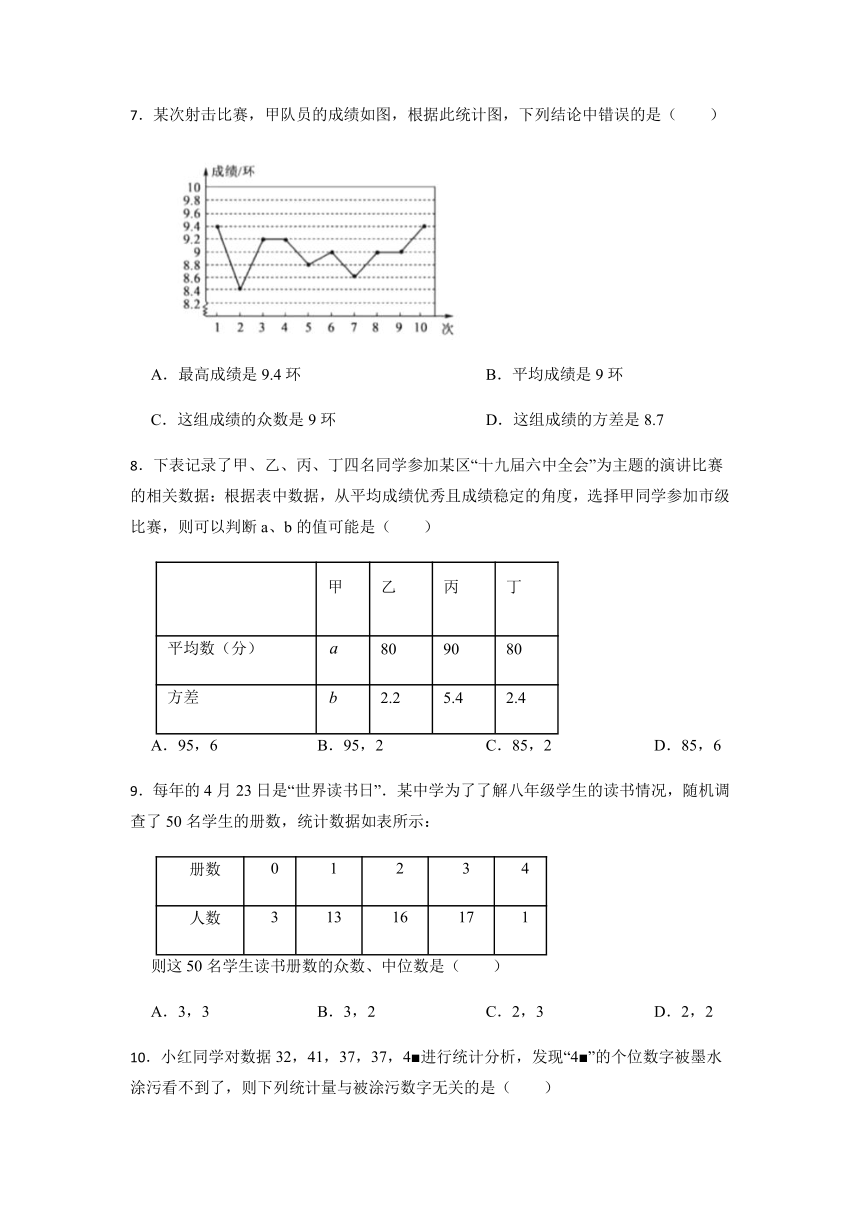
7.某次射击比赛,甲队员的成绩如图,根据此统计图,下列结论中错误的是( )
A.最高成绩是9.4环 B.平均成绩是9环
C.这组成绩的众数是9环 D.这组成绩的方差是8.7
8.下表记录了甲、乙、丙、丁四名同学参加某区“十九届六中全会”为主题的演讲比赛的相关数据:根据表中数据,从平均成绩优秀且成绩稳定的角度,选择甲同学参加市级比赛,则可以判断a、b的值可能是( )
甲 乙 丙 丁
平均数(分) 80 90 80
方差 2.2 5.4 2.4
A.95,6 B.95,2 C.85,2 D.85,6
9.每年的4月23日是“世界读书日”.某中学为了了解八年级学生的读书情况,随机调查了50名学生的册数,统计数据如表所示:
册数 0 1 2 3 4
人数 3 13 16 17 1
则这50名学生读书册数的众数、中位数是( )
A.3,3 B.3,2 C.2,3 D.2,2
10.小红同学对数据32,41,37,37,4■进行统计分析,发现“4■”的个位数字被墨水涂污看不到了,则下列统计量与被涂污数字无关的是( )
A.方差 B.平均数 C.众数 D.中位数
二、填空题
11.数据的众数有 个
12.某博物馆拟招聘一名优秀讲解员,其中小林笔试、试讲、面试三轮测试得分分别为92分,80分、85分.综合成绩中笔试占50%、试讲占30%、面试占20%,那么小林的最后得分为 分.
13.如图为某学校学生年龄分布情况扇形统计图,根据统计图,解决下列问题:
(1)m= ;
(2)该学校学生的平均年龄为 岁.
14.甲、乙、丙、丁四名同学进行跳高测试,每人10次跳高成绩的平均数都是1.28m,方差分别是S甲2=0.60,S乙2=0.62,S丙2=0.58,S丁2=0.45,则这四名同学跳高成绩最稳定的是 .
三、计算题
15.小明所在的数学兴趣小组共10名学生,在一次数学知识拓展测试中,全组的平均得分是88分,除小明外,另9名同学的得分如表(单位:分):
得分 97 91 88 86 85 84 82
人数 1 2 1 1 2 1 1
(1)小明得分是多少?
(2)求该小组此次测试得分的方差.
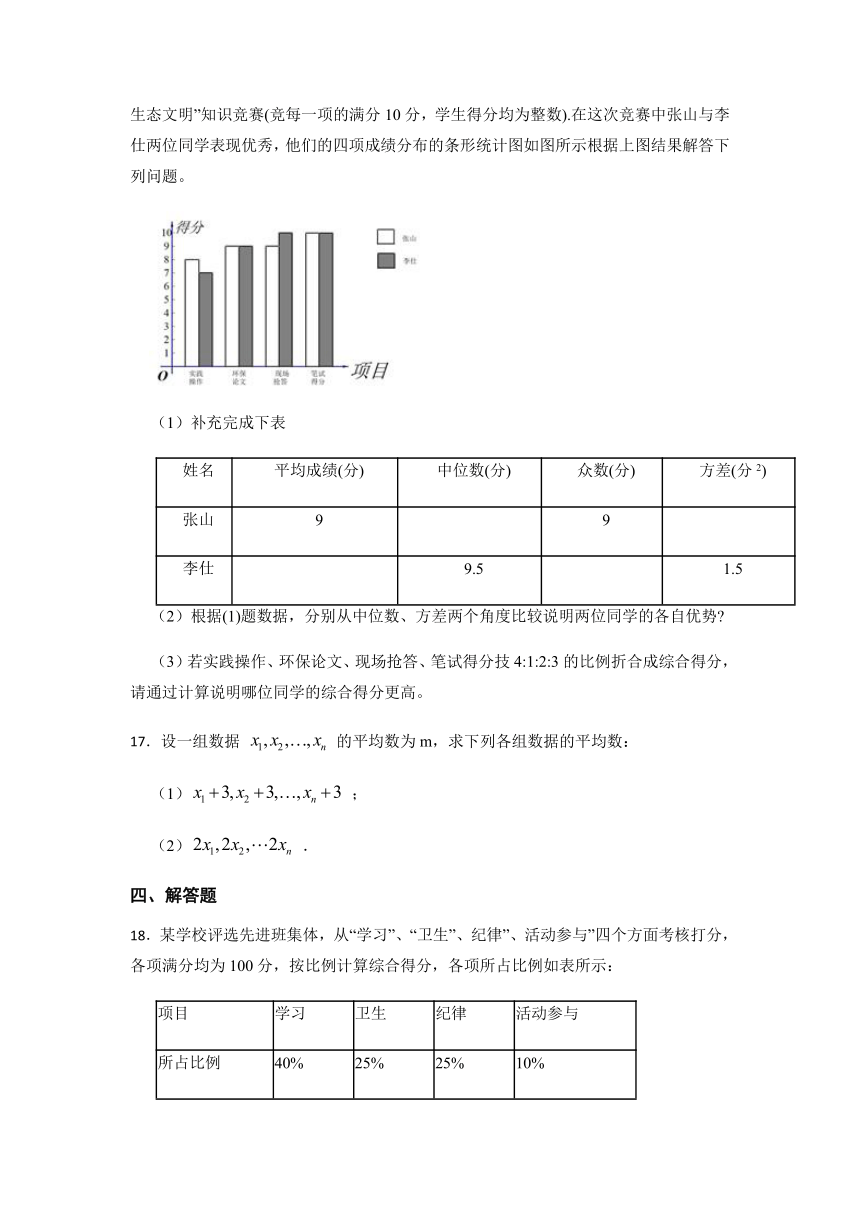
16.入为响应习近平提出的“绿水青山就是金山银山”的重要思想某校举办了“绿水青山,生态文明”知识竞赛(竞每一项的满分10分,学生得分均为整数).在这次竞赛中张山与李仕两位同学表现优秀,他们的四项成绩分布的条形统计图如图所示根据上图结果解答下列问题。
(1)补充完成下表
姓名 平均成绩(分) 中位数(分) 众数(分) 方差(分2)
张山 9 9
李仕 9.5 1.5
(2)根据(1)题数据,分别从中位数、方差两个角度比较说明两位同学的各自优势
(3)若实践操作、环保论文、现场抢答、笔试得分技4:1:2:3的比例折合成综合得分,请通过计算说明哪位同学的综合得分更高。
17.设一组数据 的平均数为m,求下列各组数据的平均数:
(1) ;
(2) .
四、解答题
18.某学校评选先进班集体,从“学习”、“卫生”、纪律”、活动参与”四个方面考核打分,各项满分均为100分,按比例计算综合得分,各项所占比例如表所示:
项目 学习 卫生 纪律 活动参与
所占比例 40% 25% 25% 10%
八年级(1)班这四项得分依次为95分,90分,88分,80分,若学校规定班级四项综合得分超过90分的将会获得先进班集体,请你通过计算说明该班是否会获得先进班集体?
19.学校运动会开设了“抢收抢种”项目,八(5)班甲,两个队伍都想代表班级参赛,为了选择一个比较好的队伍,八(5)班的班委组织了一次选拔赛,甲,乙两队各5人的比赛成绩如下表(单位:分):
甲队 7 8 10 7 9
乙对 7 8 7 9 9
经计算,甲队比赛成绩的平均数为8分,方差为1.2,请计算乙队比赛成绩的方差,并根据计算结果,帮助班委选择一个成绩比较稳定的队伍代表班级参赛.
20.某养鱼个体经营户在鱼塘放养了5500条草鱼苗,鱼苗的成活率为90%.养殖一段时间后,想估计鱼塘中产量,随机网了三次,第一次网出30条鱼,平均每条鱼的重量是1kg;第二次网出了45条鱼,平均每条鱼的重量是1.3kg;第三次网出了35条鱼,平均每条鱼的重量是1.2kg,请你估计鱼塘中鱼的总重量是多少kg?
五、综合题
21.2022年3月25日,教育部印发《义务教育课程方案和课程标准(2022年版)》,优化了课程设置,将劳动从综合实践活动课程中独立出来.某校为了解该校学生一周的课外劳动情况,随机抽取部分学生调查了他们一周的课外劳动时间,将数据进行整理并制成如下统计图.
请根据图中提供的信息,解答下面的问题:
(1)求图1中的m= ,本次调查数据的中位数是 h,本次调查数据的众数是 h;
(2)该校此次抽查的这些学生一周平均的课外劳动时间是多少?
(3)若该校共有2000名学生,请根据统计数据,估计该校学生一周的课外劳动时间不小于的人数.
22.在学校组织的“最美数学小报”的评比中,校团委给每个同学的作品打分,成绩分为四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,将八(1)班与八(2)班的成绩整理并绘制成如下统计图:
请你根据以上提供的信息解答下列问题:
(1)将表格补充完整.
平均数(分) 中位数(分) 众数(分)
八(1)班 83.75 80
八(2)班 80
(2)若八(1)班有40人,且评分为B级及以上的同学有纪念奖章,请问该班共有几位同学得到奖章?
23.随机抽取某城市一年(以365天计)中的30天的日平均气温状况统计如下:温度(℃)
温度(℃) 10 14 18 22 26 30 32
天数 3 5 5 7 6 2 2
请根据上述数据回答下列问题:
(1)估计该城市年平均气温大约是多少?
(2)写出该数据的中位数、众数;
(3)计算该城市一年中约有几天的日平均气温为26℃?
(4)若日平均气温在17℃~23℃为市民“满意温度”,则这组数据中达到市民“满意温度”的有几天?
答案解析部分
1.【答案】D
【解析】【解答】解:A、两直线平行,同位角相等,故该命题不是真命题;
B、 是整式,故该命题不是真命题;
C、 数据6,3,10的中位数是6,故该命题不是真命题;
D、 第七次全国人口普查是全面调查,故该命题是真命题.
故答案为:D.
【分析】只有在两直线平行的时候,同位角才会相等,据此判断A;“”是数与字母的乘积,是单项式,而单项式与多项式统称整式,据此判断B;将一组数据按从小到大(或者从大到小)的顺序排列后,如果数据的个数是奇数个时,则处在最中间的那个数据叫做这组数据的中位数;如果数据的个数是偶数个时,则处在最中间的两个数据的平均数 叫做这组数据的中位数,据此判断C;对调查对象的全体进行的调查就是全面调查,据此判断D.
2.【答案】A
【解析】【解答】解:在这一组数据中5是出现次数最多的,故众数是5;
处于中间位置的两个数的平均数是,故这组数据的中位数是6.
∴答案为:5、6,
故答案为:A.
【分析】众数:在一组数据中,出现次数最多的数据叫做众数,(众数可能有多个),中位数:将一组数据按从小到大(或者从大到小)的顺序排列后,如果数据的个数是奇数个时,则处在最中间的那个数据叫做这组数据的中位数;如果数据的个数是偶数个时,则处在最中间的两个数据的平均数 叫做这组数据的中位数,据此即可得出答案.
3.【答案】B
【解析】【解答】解:这两个班总平均分为=75.5(分)
故答案为:B.
【分析】求出各班的总分,再求其平均数即可.
4.【答案】C
【解析】【解答】解:∵x,1,4的中位数是3,3>x,
∴排序为:1,3,4,
∴x=3.
故答案为:C
【分析】利用求中位数的方法是:把数据先按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数;已知数中有3个数,根据这组数据的中位数是3,可得到x的值.
5.【答案】B
【解析】【解答】解:由折线统计图得:乙,丙的成绩在92附近波动,甲、丁 的成绩在91附近波动,
∴乙,丙的平均成绩高于甲、丁,
由折线统计图得:丙成绩的波动幅度小于丁成绩的波动幅度,
∴这四人中乙的平均成绩好又发挥稳定,
故答案为:B.
【分析】根据平均数和方差的意义进行判断.
6.【答案】D
【解析】【解答】解:因为销售量为30件出现的次数最多,所以这25名营销人员销售量的众数是30.
故答案为:D.
【分析】在一组数据中,出现次数最多的数据叫做众数,(众数可能有多个),据此观察表格即可得出答案.
7.【答案】D
【解析】【解答】解:A、由统计图得,最高成绩是9.4环,不符合题意;
B、平均成绩:,符合题意;
C、由统计图得,9出现了3次,出现的次数最多,不符合题意;
D、方差:,符合题意;
故答案为:D.
【分析】结合折线统计图中的数据,再利用众数、平均数、方差的定义及计算方法逐项判断即可。
8.【答案】B
【解析】【解答】解:从平均成绩优秀且成绩稳定的角度,选择甲同学参加市级比赛,说明甲的平均成绩最高且方差最低.
故答案为:B.
【分析】利用平均数和方差的定义及计算方法求解即可。
9.【答案】B
【解析】【解答】解:∵3出现了17次,是出现次数最多的数,
∴这组数据的众数是3;
∵一共有50个数,从小到大排列后,第25个数和第26个数都是2,
∴这组数据的中位数是2;
故答案为:B
【分析】求中位数的方法是:把数据先按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数;众数是一组数据中出现次数最多的数据,据此可求出这组数据的众数和中位数.
10.【答案】D
【解析】【解答】解:∵这组数据的平均数、方差和众数都与被涂污数字有关,而这组数据的中位数为37,与被涂污数字无关,
∴与被涂污数字无关的统计量是中位数.
故答案为:D
【分析】利用众数、平均数、方差和中位数的定义及计算方法逐项判断即可。
11.【答案】2
【解析】【解答】解:∵数据3,3,4,4,6中,3和4都出现了2次,是出现次数最多的数,
∴这组数据的众数是3和4,一共2个.
故答案为:2
【分析】众数是一组数据中出现次数最多的数,据此可得到这组数据的众数及众数的个数.
12.【答案】87
【解析】【解答】解:小林的最后得分为92×50%+80×30%+85×20%=87(分),
故答案为:87.
【分析】利用加权平均数公式进行计算即可.
13.【答案】(1)30
(2)13.95
【解析】【解答】解:由题意:,
所以30;
该学校学生的平均年龄
;
故答案为:30;13.95.
【分析】(1)利用扇形统计图求解即可;
(2)利用加权平均数的计算方法求解即可。
14.【答案】丁
【解析】【解答】解:∵S甲2=0.60,S乙2=0.62,S丙2=0.58,S丁2=0.45,
∴S丁2<S丙2<S甲2<S乙2,
∴这四名同学跳高成绩最稳定的是丁,
故答案为:丁.
【分析】利用方差的性质:方差越大,数据波动越大求解即可。
15.【答案】(1)解:根据题意得:,
答:小明得91分;
(2)解:
答:该小组此次测试得分的方差为18.2
【解析】【分析】(1)根据平均分乘以总人数可得总得分,由表格中的数据可得除小明外,另9名同学的总成绩,据此不难求出小明的得分;
(2)直接根据方差的计算公式进行计算即可求出方差.
16.【答案】(1)解:张山的得分为:8,9,9,10,
最中间的数是9和9
∴张山得分对的中位数为:(9+9)÷2=9;
方差为:
李仕的得分:7,9,10,10,
平均成绩为:
10出现了2次,是出现次数最多的数,
∴李仕得分的众数为10;
姓名 平均成绩(分) 中位数(分) 众数(分) 方差(分2)
张山 9 9 9 0.5
李仕 9 9.5 10 1.5
(2)从中位数角度考虑,李仕大于张山,说明李仕高分项目多;
从反差角度考虑,李仕大于张山,说明张山各项成绩均衡。
(3)张山的综合得分为:分;
李仕的综合得分为:分;
8.9>8.7.
∴张山的综合得分更高.
【解析】【分析】(1)从条形统计图中可得到四项成绩,利用中位数的定义和方差的计算方法可求出张山的中位数和方差;再利用平均数公式,可求出李仕的平均分,根据众数是一组数据中出现次数最多的数,可求出李仕成绩的众数。
(2)从表中的各项数据,从不同的角度进行分析即可。
(3)根据实践操作、环保论文、现场抢答、笔试得分技4:1:2:3的比例折合成综合得分,利用加权平均数公式,分别求出张山和李仕的综合平均成绩,再比较大小,可作出判断。
17.【答案】(1)解:即 ,
则 .
,
,
的平均数是 ;
(2)解: ,
,
的平均数是 .
【解析】【分析】(1) 首先根据求平均数的公式: ,求 ,然后按照平均数公式求出 的平均数;
(2)
首先根据求平均数的公式: ,求 ,然后按照平均数公式求出 的平均数;
18.【答案】解:根据题意得:
(分),
∵ ,
∴八年级(1)班会获得先进班集体.
【解析】【分析】利用加权平均数公式,结合表中数据,进行计算,将其结果与90比较大小可作出判断.
19.【答案】解: (分 ,
所以乙队比赛成绩的平均数为8分.
所以乙队比赛成绩的方差是0.8.
因为两队比赛成绩的平均数相等,且 ,
所以选择乙队代表班级参加学校比赛.
【解析】【分析】利用平均数公式求出乙队比赛成绩的平均数;再利用方差公式求出乙队比赛成绩的方差;可得到两个队的平均成绩一样,根据方差越小,成绩越稳定,即可求解.
20.【答案】解:由题意得: kg.
答:估计鱼塘中鱼的总重量是5872.5kg.
【解析】【分析】先求出样本平均数,然后乘以5500,再乘以90%即得结论.
21.【答案】(1)25;15;15
(2)解:此次抽查的这些学生一周平均的课外劳动时间是小时,
答:此次抽查的这些学生一周平均的课外劳动时间是小时;
(3)解:(人)
答:估计该校学生一周的课外劳动时间不小于的人数为人.
【解析】【解答】解:(1),
∴,
中位数为第与个数的平均数,即,
由条形统计图可知,众数为,
故答案为:;
【分析】(1)利用4小时的人数除以总人数,然后乘以100%可得m的值,将数据按照由小到大的顺序进行排列,求出中间两个数据的平均数即为中位数,找出出现次数最多的数据即为众数;
(2)利用小时数×对应的人数,然后除以总人数即可求出一周的平均劳动时间;
(3)利用劳动时间为3、4、5小时的人数之和除以总人数,然后乘以2000即可.
22.【答案】(1)解:
平均数(分) 中位数(分) 众数(分)
八(1)班 83.75 80 ③80
八(2)班 ①85.25 ②80 80
①
②总计40个数据,从小到大排列得第20、21位数字都是80分,所以中位数为80
③众数即目标样本内相同数字最多的数,由扇形图可知C级所占比例最高,所以众数为80
(2)解:由统计图可知B级及以上的同学所占比例分别为17.5%和22.5%,计算可得:(人)
【解析】【分析】(1)根据各个等级的得分乘以对应的人数,然后除以总人数可得平均数,将八(2)班的成绩按照从小到大的顺序进行排列,求出第20、21个数据的平均数即为中位数,找出八(1)班所占比例最高的等级所对应的成绩即为众数;
(2)由统计图可知B级及以上的同学所占比例分别为17.5%和22.5%,利用比例之和乘以40即可.
23.【答案】(1)解:30天的日平均气温20.8
答:估计该城市年平均气温大约是20.8℃;
(2)解:将这组数据按从小到大排列为10、10、10、14、14、14、14、14、18、18、18、18、18、22、22、22、22、22、22、22、26、26、26、26、26、26、30、30、32、32,
由于有30个数,取第15、16位都是22,则中位数为22;
因为22出现的次数最多,则该组数据的众数为22;
(3)解:一年中日平均气温为26℃的天数为365÷30×6≈73天
(4)解:这组数据中达到市民“满意温度”的天数为5+7=12天.
【解析】【分析】(1)根据加权平均数的计算方法即可算出答案;
(2)众数:在一组数据中,出现次数最多的数据叫做众数,(众数可能有多个),中位数:将一组数据按从小到大(或者从大到小)的顺序排列后,如果数据的个数是奇数个时,则处在最中间的那个数据叫做这组数据的中位数;如果数据的个数是偶数个时,则处在最中间的两个数据的平均数 叫做这组数据的中位数,据此即可得出答案;
(3)利用样本估计总体的方法,用365乘以样本中日平均气温为26℃所占的百分比即可估算出该城市一年中约有多少天日平均气温为26℃ ;
(4)利用表格提供的数据,数出日平均气温在17℃~23℃的天数即可.
一、单选题
1.下列命题是真命题的是( )
A.同位角相等
B.不是整式
C.数据6,3,10的中位数是3
D.第七次全国人口普查是全面调查
2.某校男子篮球队10名队员进行定点投篮练习,每人投篮10次,将他们投中的次数进行统计制成下表:则这10名队员投中的次数组成的一组数据中,众数和中位数分别为( )
投中次数 3 5 6 7 8 9
人数 1 3 2 2 1 1
A.5,6 B.2,6 C.5,5 D.6,5
3.某次数学测验中,八(1)班55人平均分为80分,八(2)班45人平均分为70分,则这两个班总平均分为( )
A.75分 B.75.5分 C.76分 D.76.5分
4.若一组数据的中位数为3,则的值为( )
A.1 B.2 C.3 D.4
5.甲、乙、丙、丁四人10次随堂测验的成绩如图所示,从图中可以看出这10次测验平均成绩较高且较稳定的是( )
A.
B.
C.
D.
6.某公司对25名营销人员4月份销售某种商品的情况统计如下:
销售量(件) 60 50 40 35 30 20
人数 1 4 4 6 7 3
则这25名营销人员销售量的众数是( )
A.50 B.40 C.35 D.30
7.某次射击比赛,甲队员的成绩如图,根据此统计图,下列结论中错误的是( )
A.最高成绩是9.4环 B.平均成绩是9环
C.这组成绩的众数是9环 D.这组成绩的方差是8.7
8.下表记录了甲、乙、丙、丁四名同学参加某区“十九届六中全会”为主题的演讲比赛的相关数据:根据表中数据,从平均成绩优秀且成绩稳定的角度,选择甲同学参加市级比赛,则可以判断a、b的值可能是( )
甲 乙 丙 丁
平均数(分) 80 90 80
方差 2.2 5.4 2.4
A.95,6 B.95,2 C.85,2 D.85,6
9.每年的4月23日是“世界读书日”.某中学为了了解八年级学生的读书情况,随机调查了50名学生的册数,统计数据如表所示:
册数 0 1 2 3 4
人数 3 13 16 17 1
则这50名学生读书册数的众数、中位数是( )
A.3,3 B.3,2 C.2,3 D.2,2
10.小红同学对数据32,41,37,37,4■进行统计分析,发现“4■”的个位数字被墨水涂污看不到了,则下列统计量与被涂污数字无关的是( )
A.方差 B.平均数 C.众数 D.中位数
二、填空题
11.数据的众数有 个
12.某博物馆拟招聘一名优秀讲解员,其中小林笔试、试讲、面试三轮测试得分分别为92分,80分、85分.综合成绩中笔试占50%、试讲占30%、面试占20%,那么小林的最后得分为 分.
13.如图为某学校学生年龄分布情况扇形统计图,根据统计图,解决下列问题:
(1)m= ;
(2)该学校学生的平均年龄为 岁.
14.甲、乙、丙、丁四名同学进行跳高测试,每人10次跳高成绩的平均数都是1.28m,方差分别是S甲2=0.60,S乙2=0.62,S丙2=0.58,S丁2=0.45,则这四名同学跳高成绩最稳定的是 .
三、计算题
15.小明所在的数学兴趣小组共10名学生,在一次数学知识拓展测试中,全组的平均得分是88分,除小明外,另9名同学的得分如表(单位:分):
得分 97 91 88 86 85 84 82
人数 1 2 1 1 2 1 1
(1)小明得分是多少?
(2)求该小组此次测试得分的方差.
16.入为响应习近平提出的“绿水青山就是金山银山”的重要思想某校举办了“绿水青山,生态文明”知识竞赛(竞每一项的满分10分,学生得分均为整数).在这次竞赛中张山与李仕两位同学表现优秀,他们的四项成绩分布的条形统计图如图所示根据上图结果解答下列问题。
(1)补充完成下表
姓名 平均成绩(分) 中位数(分) 众数(分) 方差(分2)
张山 9 9
李仕 9.5 1.5
(2)根据(1)题数据,分别从中位数、方差两个角度比较说明两位同学的各自优势
(3)若实践操作、环保论文、现场抢答、笔试得分技4:1:2:3的比例折合成综合得分,请通过计算说明哪位同学的综合得分更高。
17.设一组数据 的平均数为m,求下列各组数据的平均数:
(1) ;
(2) .
四、解答题
18.某学校评选先进班集体,从“学习”、“卫生”、纪律”、活动参与”四个方面考核打分,各项满分均为100分,按比例计算综合得分,各项所占比例如表所示:
项目 学习 卫生 纪律 活动参与
所占比例 40% 25% 25% 10%
八年级(1)班这四项得分依次为95分,90分,88分,80分,若学校规定班级四项综合得分超过90分的将会获得先进班集体,请你通过计算说明该班是否会获得先进班集体?
19.学校运动会开设了“抢收抢种”项目,八(5)班甲,两个队伍都想代表班级参赛,为了选择一个比较好的队伍,八(5)班的班委组织了一次选拔赛,甲,乙两队各5人的比赛成绩如下表(单位:分):
甲队 7 8 10 7 9
乙对 7 8 7 9 9
经计算,甲队比赛成绩的平均数为8分,方差为1.2,请计算乙队比赛成绩的方差,并根据计算结果,帮助班委选择一个成绩比较稳定的队伍代表班级参赛.
20.某养鱼个体经营户在鱼塘放养了5500条草鱼苗,鱼苗的成活率为90%.养殖一段时间后,想估计鱼塘中产量,随机网了三次,第一次网出30条鱼,平均每条鱼的重量是1kg;第二次网出了45条鱼,平均每条鱼的重量是1.3kg;第三次网出了35条鱼,平均每条鱼的重量是1.2kg,请你估计鱼塘中鱼的总重量是多少kg?
五、综合题
21.2022年3月25日,教育部印发《义务教育课程方案和课程标准(2022年版)》,优化了课程设置,将劳动从综合实践活动课程中独立出来.某校为了解该校学生一周的课外劳动情况,随机抽取部分学生调查了他们一周的课外劳动时间,将数据进行整理并制成如下统计图.
请根据图中提供的信息,解答下面的问题:
(1)求图1中的m= ,本次调查数据的中位数是 h,本次调查数据的众数是 h;
(2)该校此次抽查的这些学生一周平均的课外劳动时间是多少?
(3)若该校共有2000名学生,请根据统计数据,估计该校学生一周的课外劳动时间不小于的人数.
22.在学校组织的“最美数学小报”的评比中,校团委给每个同学的作品打分,成绩分为四个等级,其中相应等级的得分依次记为100分,90分,80分,70分,将八(1)班与八(2)班的成绩整理并绘制成如下统计图:
请你根据以上提供的信息解答下列问题:
(1)将表格补充完整.
平均数(分) 中位数(分) 众数(分)
八(1)班 83.75 80
八(2)班 80
(2)若八(1)班有40人,且评分为B级及以上的同学有纪念奖章,请问该班共有几位同学得到奖章?
23.随机抽取某城市一年(以365天计)中的30天的日平均气温状况统计如下:温度(℃)
温度(℃) 10 14 18 22 26 30 32
天数 3 5 5 7 6 2 2
请根据上述数据回答下列问题:
(1)估计该城市年平均气温大约是多少?
(2)写出该数据的中位数、众数;
(3)计算该城市一年中约有几天的日平均气温为26℃?
(4)若日平均气温在17℃~23℃为市民“满意温度”,则这组数据中达到市民“满意温度”的有几天?
答案解析部分
1.【答案】D
【解析】【解答】解:A、两直线平行,同位角相等,故该命题不是真命题;
B、 是整式,故该命题不是真命题;
C、 数据6,3,10的中位数是6,故该命题不是真命题;
D、 第七次全国人口普查是全面调查,故该命题是真命题.
故答案为:D.
【分析】只有在两直线平行的时候,同位角才会相等,据此判断A;“”是数与字母的乘积,是单项式,而单项式与多项式统称整式,据此判断B;将一组数据按从小到大(或者从大到小)的顺序排列后,如果数据的个数是奇数个时,则处在最中间的那个数据叫做这组数据的中位数;如果数据的个数是偶数个时,则处在最中间的两个数据的平均数 叫做这组数据的中位数,据此判断C;对调查对象的全体进行的调查就是全面调查,据此判断D.
2.【答案】A
【解析】【解答】解:在这一组数据中5是出现次数最多的,故众数是5;
处于中间位置的两个数的平均数是,故这组数据的中位数是6.
∴答案为:5、6,
故答案为:A.
【分析】众数:在一组数据中,出现次数最多的数据叫做众数,(众数可能有多个),中位数:将一组数据按从小到大(或者从大到小)的顺序排列后,如果数据的个数是奇数个时,则处在最中间的那个数据叫做这组数据的中位数;如果数据的个数是偶数个时,则处在最中间的两个数据的平均数 叫做这组数据的中位数,据此即可得出答案.
3.【答案】B
【解析】【解答】解:这两个班总平均分为=75.5(分)
故答案为:B.
【分析】求出各班的总分,再求其平均数即可.
4.【答案】C
【解析】【解答】解:∵x,1,4的中位数是3,3>x,
∴排序为:1,3,4,
∴x=3.
故答案为:C
【分析】利用求中位数的方法是:把数据先按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数;已知数中有3个数,根据这组数据的中位数是3,可得到x的值.
5.【答案】B
【解析】【解答】解:由折线统计图得:乙,丙的成绩在92附近波动,甲、丁 的成绩在91附近波动,
∴乙,丙的平均成绩高于甲、丁,
由折线统计图得:丙成绩的波动幅度小于丁成绩的波动幅度,
∴这四人中乙的平均成绩好又发挥稳定,
故答案为:B.
【分析】根据平均数和方差的意义进行判断.
6.【答案】D
【解析】【解答】解:因为销售量为30件出现的次数最多,所以这25名营销人员销售量的众数是30.
故答案为:D.
【分析】在一组数据中,出现次数最多的数据叫做众数,(众数可能有多个),据此观察表格即可得出答案.
7.【答案】D
【解析】【解答】解:A、由统计图得,最高成绩是9.4环,不符合题意;
B、平均成绩:,符合题意;
C、由统计图得,9出现了3次,出现的次数最多,不符合题意;
D、方差:,符合题意;
故答案为:D.
【分析】结合折线统计图中的数据,再利用众数、平均数、方差的定义及计算方法逐项判断即可。
8.【答案】B
【解析】【解答】解:从平均成绩优秀且成绩稳定的角度,选择甲同学参加市级比赛,说明甲的平均成绩最高且方差最低.
故答案为:B.
【分析】利用平均数和方差的定义及计算方法求解即可。
9.【答案】B
【解析】【解答】解:∵3出现了17次,是出现次数最多的数,
∴这组数据的众数是3;
∵一共有50个数,从小到大排列后,第25个数和第26个数都是2,
∴这组数据的中位数是2;
故答案为:B
【分析】求中位数的方法是:把数据先按从小到大的顺序排列,位于最中间的一个数(或两个数的平均数)为中位数;众数是一组数据中出现次数最多的数据,据此可求出这组数据的众数和中位数.
10.【答案】D
【解析】【解答】解:∵这组数据的平均数、方差和众数都与被涂污数字有关,而这组数据的中位数为37,与被涂污数字无关,
∴与被涂污数字无关的统计量是中位数.
故答案为:D
【分析】利用众数、平均数、方差和中位数的定义及计算方法逐项判断即可。
11.【答案】2
【解析】【解答】解:∵数据3,3,4,4,6中,3和4都出现了2次,是出现次数最多的数,
∴这组数据的众数是3和4,一共2个.
故答案为:2
【分析】众数是一组数据中出现次数最多的数,据此可得到这组数据的众数及众数的个数.
12.【答案】87
【解析】【解答】解:小林的最后得分为92×50%+80×30%+85×20%=87(分),
故答案为:87.
【分析】利用加权平均数公式进行计算即可.
13.【答案】(1)30
(2)13.95
【解析】【解答】解:由题意:,
所以30;
该学校学生的平均年龄
;
故答案为:30;13.95.
【分析】(1)利用扇形统计图求解即可;
(2)利用加权平均数的计算方法求解即可。
14.【答案】丁
【解析】【解答】解:∵S甲2=0.60,S乙2=0.62,S丙2=0.58,S丁2=0.45,
∴S丁2<S丙2<S甲2<S乙2,
∴这四名同学跳高成绩最稳定的是丁,
故答案为:丁.
【分析】利用方差的性质:方差越大,数据波动越大求解即可。
15.【答案】(1)解:根据题意得:,
答:小明得91分;
(2)解:
答:该小组此次测试得分的方差为18.2
【解析】【分析】(1)根据平均分乘以总人数可得总得分,由表格中的数据可得除小明外,另9名同学的总成绩,据此不难求出小明的得分;
(2)直接根据方差的计算公式进行计算即可求出方差.
16.【答案】(1)解:张山的得分为:8,9,9,10,
最中间的数是9和9
∴张山得分对的中位数为:(9+9)÷2=9;
方差为:
李仕的得分:7,9,10,10,
平均成绩为:
10出现了2次,是出现次数最多的数,
∴李仕得分的众数为10;
姓名 平均成绩(分) 中位数(分) 众数(分) 方差(分2)
张山 9 9 9 0.5
李仕 9 9.5 10 1.5
(2)从中位数角度考虑,李仕大于张山,说明李仕高分项目多;
从反差角度考虑,李仕大于张山,说明张山各项成绩均衡。
(3)张山的综合得分为:分;
李仕的综合得分为:分;
8.9>8.7.
∴张山的综合得分更高.
【解析】【分析】(1)从条形统计图中可得到四项成绩,利用中位数的定义和方差的计算方法可求出张山的中位数和方差;再利用平均数公式,可求出李仕的平均分,根据众数是一组数据中出现次数最多的数,可求出李仕成绩的众数。
(2)从表中的各项数据,从不同的角度进行分析即可。
(3)根据实践操作、环保论文、现场抢答、笔试得分技4:1:2:3的比例折合成综合得分,利用加权平均数公式,分别求出张山和李仕的综合平均成绩,再比较大小,可作出判断。
17.【答案】(1)解:即 ,
则 .
,
,
的平均数是 ;
(2)解: ,
,
的平均数是 .
【解析】【分析】(1) 首先根据求平均数的公式: ,求 ,然后按照平均数公式求出 的平均数;
(2)
首先根据求平均数的公式: ,求 ,然后按照平均数公式求出 的平均数;
18.【答案】解:根据题意得:
(分),
∵ ,
∴八年级(1)班会获得先进班集体.
【解析】【分析】利用加权平均数公式,结合表中数据,进行计算,将其结果与90比较大小可作出判断.
19.【答案】解: (分 ,
所以乙队比赛成绩的平均数为8分.
所以乙队比赛成绩的方差是0.8.
因为两队比赛成绩的平均数相等,且 ,
所以选择乙队代表班级参加学校比赛.
【解析】【分析】利用平均数公式求出乙队比赛成绩的平均数;再利用方差公式求出乙队比赛成绩的方差;可得到两个队的平均成绩一样,根据方差越小,成绩越稳定,即可求解.
20.【答案】解:由题意得: kg.
答:估计鱼塘中鱼的总重量是5872.5kg.
【解析】【分析】先求出样本平均数,然后乘以5500,再乘以90%即得结论.
21.【答案】(1)25;15;15
(2)解:此次抽查的这些学生一周平均的课外劳动时间是小时,
答:此次抽查的这些学生一周平均的课外劳动时间是小时;
(3)解:(人)
答:估计该校学生一周的课外劳动时间不小于的人数为人.
【解析】【解答】解:(1),
∴,
中位数为第与个数的平均数,即,
由条形统计图可知,众数为,
故答案为:;
【分析】(1)利用4小时的人数除以总人数,然后乘以100%可得m的值,将数据按照由小到大的顺序进行排列,求出中间两个数据的平均数即为中位数,找出出现次数最多的数据即为众数;
(2)利用小时数×对应的人数,然后除以总人数即可求出一周的平均劳动时间;
(3)利用劳动时间为3、4、5小时的人数之和除以总人数,然后乘以2000即可.
22.【答案】(1)解:
平均数(分) 中位数(分) 众数(分)
八(1)班 83.75 80 ③80
八(2)班 ①85.25 ②80 80
①
②总计40个数据,从小到大排列得第20、21位数字都是80分,所以中位数为80
③众数即目标样本内相同数字最多的数,由扇形图可知C级所占比例最高,所以众数为80
(2)解:由统计图可知B级及以上的同学所占比例分别为17.5%和22.5%,计算可得:(人)
【解析】【分析】(1)根据各个等级的得分乘以对应的人数,然后除以总人数可得平均数,将八(2)班的成绩按照从小到大的顺序进行排列,求出第20、21个数据的平均数即为中位数,找出八(1)班所占比例最高的等级所对应的成绩即为众数;
(2)由统计图可知B级及以上的同学所占比例分别为17.5%和22.5%,利用比例之和乘以40即可.
23.【答案】(1)解:30天的日平均气温20.8
答:估计该城市年平均气温大约是20.8℃;
(2)解:将这组数据按从小到大排列为10、10、10、14、14、14、14、14、18、18、18、18、18、22、22、22、22、22、22、22、26、26、26、26、26、26、30、30、32、32,
由于有30个数,取第15、16位都是22,则中位数为22;
因为22出现的次数最多,则该组数据的众数为22;
(3)解:一年中日平均气温为26℃的天数为365÷30×6≈73天
(4)解:这组数据中达到市民“满意温度”的天数为5+7=12天.
【解析】【分析】(1)根据加权平均数的计算方法即可算出答案;
(2)众数:在一组数据中,出现次数最多的数据叫做众数,(众数可能有多个),中位数:将一组数据按从小到大(或者从大到小)的顺序排列后,如果数据的个数是奇数个时,则处在最中间的那个数据叫做这组数据的中位数;如果数据的个数是偶数个时,则处在最中间的两个数据的平均数 叫做这组数据的中位数,据此即可得出答案;
(3)利用样本估计总体的方法,用365乘以样本中日平均气温为26℃所占的百分比即可估算出该城市一年中约有多少天日平均气温为26℃ ;
(4)利用表格提供的数据,数出日平均气温在17℃~23℃的天数即可.
