数学人教A版(2019)必修第一册4.2.2 指数函数的图象和性质 课件(共46张ppt)
文档属性
| 名称 | 数学人教A版(2019)必修第一册4.2.2 指数函数的图象和性质 课件(共46张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 5.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-05 00:00:00 | ||
图片预览








文档简介
(共46张PPT)
人教A版
高中数学 · 必修一
指数函数的图象与性质
第四章 指数 4.2.2
学习目标
能用描点法或借助信息技术画出具体指数函数的图象,探索并理解指数函数的单调性与特殊点;
通过指数函数的研究,进一步体会函数研究的基本方法;
01
02
能够应用指数函数的图象和性质解决相关问题.
03
核心素养
【数学抽象】
指数函数的图像与性质;
【逻辑推理】
类比法学习指数函数性质;
【数学运算】
运用指数函数性质解决问题;
【数学建模】
在实际问题中建立指数函数模型.
01
指数函数的概念
知识回顾
一般地,函数叫做指数函数.
其中指数是自变量,定义域是.
指数函数的概念
课程导入
研究函数的一般方法:
一 一
图象
性质
概念
定义域、值域、单调性、奇偶性等
列表、描点、连线
02
指数函数的性质
问题探究
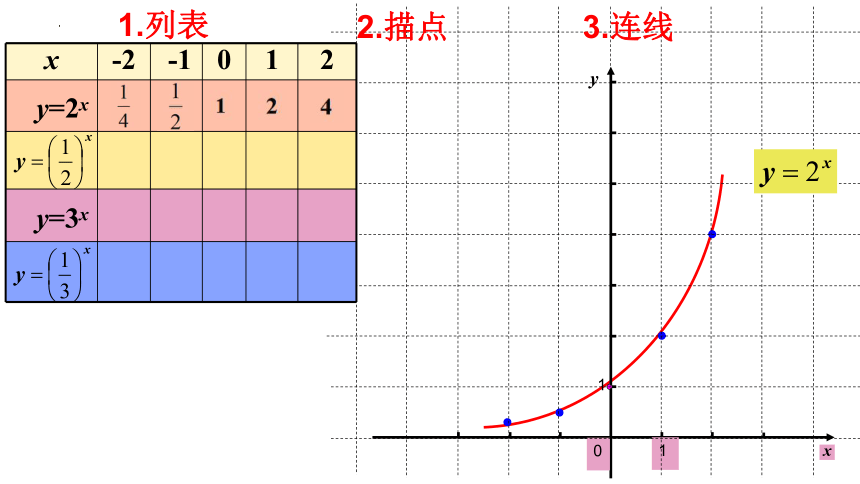
画函数图象的步骤:
列表
描点
连线
作出下列两组函数的图象:
(1)
(2)
0
1
1
2.描点 3.连线
x -2 -1 0 1 2
y=2x
y=3x
1.列表
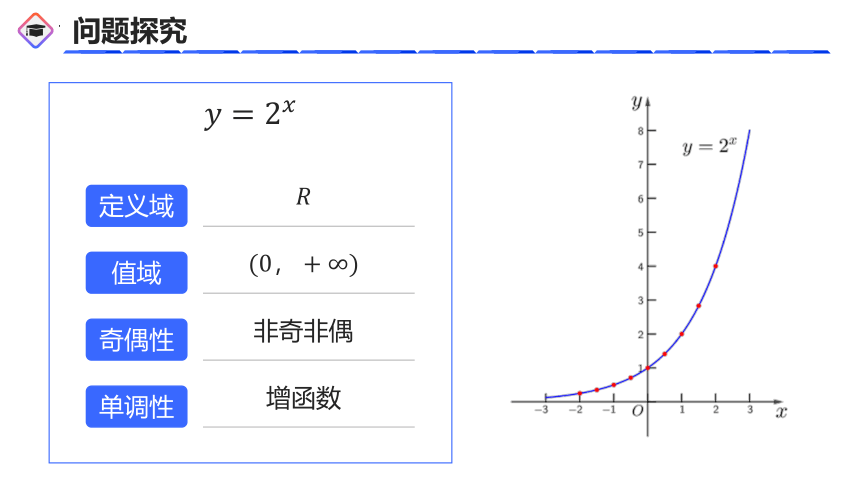
问题探究
非奇非偶
增函数
定义域
值域
奇偶性
单调性
0
1
1
2.描点 3.连线
x -2 -1 0 1 2
y=2x
y=3x
1.列表
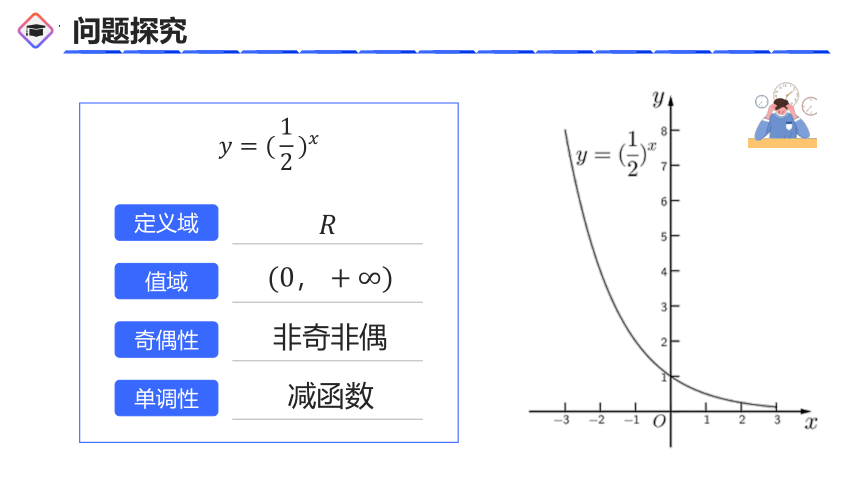
问题探究
非奇非偶
减函数
定义域
值域
奇偶性
单调性
问题探究
0
1
1
2.描点 3.连线
x -2 -1 0 1 2
y=2x
y=3x
1.列表
底数互为倒数的两个指数函数的图象关于 y 轴 对称
底数有无关系?
图象有无关系?
问题探究
将指数函数的图象按底数的取值,分为和
两种类型进行研究.
问题1:图象分别在哪几个象限?
Ⅰ、Ⅱ
定义域:____
值域:_____.
问题2:图象定义域和值域范围?
(0, +∞)
R
问题探究
将指数函数的图象按底数的取值,分为和
两种类型进行研究.
问题3:图象的上升、下降与底数
有联系吗?
当底数_____时图象上升;
当底数_____时图象下降.
问题4:图象都经过了哪个特殊
的点?为什么?
(0,1),即=0,=1
指数函数的图象和性质
图象
定义域
值域
定点 单调性
减函数
增函数
过定点,即时,
指数函数的图象和性质
当时,;
当时,;
当时,.
当时,;
当时,;
当时,.
函数值y的变化情况
对称性
函数与的图象关于轴对称.
奇偶性
非奇非偶函数.
03
指数函数性质的应用
(一)指数型函数图象过定点问题
例1
已知函数的图象恒过定点P,则定点P的坐标是 .
练习
函数的图象过定点 .
(二)指数式的大小比较
例2
比较下列各组数的大小:
,
利用幂函数单调性比较大小:
(二)指数式的大小比较
例2
比较下列各组数的大小:
(二)指数式的大小比较
例2
比较下列各组数的大小:
解题方法
指数幂的大小比较问题的三种类型及解法
底数相同,指数不同:
利用指数函数的单调性判断大小.
底数不同,指数相同:
利用幂函数的单调性判断大小.
底数不同,指数不同:
一般借助中间值(0,1等)判断大小.
(也可借助函数的图象判断)
(三)解指数型不等式
例3
求满足下列条件的的取值范围:
(三)解指数型不等式
例3
求满足下列条件的的取值范围:
解题方法
解指数不等式的类型及解法
形如 :
借助单调性得和的大小关系.
形如 :
把化为为底的指数幂形式,再借助单调性得和的大小关系.
(四)指数函数的图象识别
例4
已知,则指数函数①,②的图象为( )
C
跟踪训练
如图是指数函数的图象,
则a,b,c,d与1的大小关系是
.
(五)指数函数的图象变换
例5
课堂小结
指数函数图像的基本变换
平移变换
图象
向左平移个单位长度
的图象
向右平移个单位长度
向上平移个单位长度
向下平移个单位长度
的图象
的图象
的图象
课堂小结
对称变换
图象
关于x轴对称
的图象
关于y轴对称
关于原点对称
的图象
的图象
翻折变换
图象
保留y轴右侧的图象,并作其关于y轴的对称图形
的图象
图象
保留x轴上方的图象,并x轴下方图象翻折到x轴上方
的图象
随堂练习
函数的图象如图所示,其中为常数,则下列结论正确的是( )
A. B.
C. D.
(六)指数型函数的定义域、值域
例6
(六)指数型函数的定义域、值域、单调性
例6
(六)指数型函数的定义域、值域、单调性
例6
(六)指数型函数的定义域、值域、单调性
例6
(六)指数型函数的定义域、值域、单调性
例6
04
小结
课堂总结
请同学们根据本节课的内容画出思维导图:
随堂练习
1、已知,则的大小关系为( )
A. B.
C. D.
【解析】
∵ 增函数, , ,
C
∴ ,即
随堂练习
3、 若,则的取值范围是 ( )
A. B.
C. D.
【解析】
∵ ,且 增函数,
D
∴ , ∴ .
随堂练习
4、 已知函数
(1)求此函数的定义域,值域.
(2)确定函数的单调区间.
【解析】
(1)定义域为R,
∵ ,
∴ ,
∴ 函数的值域为.
随堂练习
(2)令 ,
则 .
∵ ,∴ 为减函数,
又∵ 在上单调递减,在上单调递增.
∴ 函数的单调递增区间为,单调递减区间为.
谢谢观看
人教A版
高中数学 · 必修一
人教A版
高中数学 · 必修一
指数函数的图象与性质
第四章 指数 4.2.2
学习目标
能用描点法或借助信息技术画出具体指数函数的图象,探索并理解指数函数的单调性与特殊点;
通过指数函数的研究,进一步体会函数研究的基本方法;
01
02
能够应用指数函数的图象和性质解决相关问题.
03
核心素养
【数学抽象】
指数函数的图像与性质;
【逻辑推理】
类比法学习指数函数性质;
【数学运算】
运用指数函数性质解决问题;
【数学建模】
在实际问题中建立指数函数模型.
01
指数函数的概念
知识回顾
一般地,函数叫做指数函数.
其中指数是自变量,定义域是.
指数函数的概念
课程导入
研究函数的一般方法:
一 一
图象
性质
概念
定义域、值域、单调性、奇偶性等
列表、描点、连线
02
指数函数的性质
问题探究
画函数图象的步骤:
列表
描点
连线
作出下列两组函数的图象:
(1)
(2)
0
1
1
2.描点 3.连线
x -2 -1 0 1 2
y=2x
y=3x
1.列表
问题探究
非奇非偶
增函数
定义域
值域
奇偶性
单调性
0
1
1
2.描点 3.连线
x -2 -1 0 1 2
y=2x
y=3x
1.列表
问题探究
非奇非偶
减函数
定义域
值域
奇偶性
单调性
问题探究
0
1
1
2.描点 3.连线
x -2 -1 0 1 2
y=2x
y=3x
1.列表
底数互为倒数的两个指数函数的图象关于 y 轴 对称
底数有无关系?
图象有无关系?
问题探究
将指数函数的图象按底数的取值,分为和
两种类型进行研究.
问题1:图象分别在哪几个象限?
Ⅰ、Ⅱ
定义域:____
值域:_____.
问题2:图象定义域和值域范围?
(0, +∞)
R
问题探究
将指数函数的图象按底数的取值,分为和
两种类型进行研究.
问题3:图象的上升、下降与底数
有联系吗?
当底数_____时图象上升;
当底数_____时图象下降.
问题4:图象都经过了哪个特殊
的点?为什么?
(0,1),即=0,=1
指数函数的图象和性质
图象
定义域
值域
定点 单调性
减函数
增函数
过定点,即时,
指数函数的图象和性质
当时,;
当时,;
当时,.
当时,;
当时,;
当时,.
函数值y的变化情况
对称性
函数与的图象关于轴对称.
奇偶性
非奇非偶函数.
03
指数函数性质的应用
(一)指数型函数图象过定点问题
例1
已知函数的图象恒过定点P,则定点P的坐标是 .
练习
函数的图象过定点 .
(二)指数式的大小比较
例2
比较下列各组数的大小:
,
利用幂函数单调性比较大小:
(二)指数式的大小比较
例2
比较下列各组数的大小:
(二)指数式的大小比较
例2
比较下列各组数的大小:
解题方法
指数幂的大小比较问题的三种类型及解法
底数相同,指数不同:
利用指数函数的单调性判断大小.
底数不同,指数相同:
利用幂函数的单调性判断大小.
底数不同,指数不同:
一般借助中间值(0,1等)判断大小.
(也可借助函数的图象判断)
(三)解指数型不等式
例3
求满足下列条件的的取值范围:
(三)解指数型不等式
例3
求满足下列条件的的取值范围:
解题方法
解指数不等式的类型及解法
形如 :
借助单调性得和的大小关系.
形如 :
把化为为底的指数幂形式,再借助单调性得和的大小关系.
(四)指数函数的图象识别
例4
已知,则指数函数①,②的图象为( )
C
跟踪训练
如图是指数函数的图象,
则a,b,c,d与1的大小关系是
.
(五)指数函数的图象变换
例5
课堂小结
指数函数图像的基本变换
平移变换
图象
向左平移个单位长度
的图象
向右平移个单位长度
向上平移个单位长度
向下平移个单位长度
的图象
的图象
的图象
课堂小结
对称变换
图象
关于x轴对称
的图象
关于y轴对称
关于原点对称
的图象
的图象
翻折变换
图象
保留y轴右侧的图象,并作其关于y轴的对称图形
的图象
图象
保留x轴上方的图象,并x轴下方图象翻折到x轴上方
的图象
随堂练习
函数的图象如图所示,其中为常数,则下列结论正确的是( )
A. B.
C. D.
(六)指数型函数的定义域、值域
例6
(六)指数型函数的定义域、值域、单调性
例6
(六)指数型函数的定义域、值域、单调性
例6
(六)指数型函数的定义域、值域、单调性
例6
(六)指数型函数的定义域、值域、单调性
例6
04
小结
课堂总结
请同学们根据本节课的内容画出思维导图:
随堂练习
1、已知,则的大小关系为( )
A. B.
C. D.
【解析】
∵ 增函数, , ,
C
∴ ,即
随堂练习
3、 若,则的取值范围是 ( )
A. B.
C. D.
【解析】
∵ ,且 增函数,
D
∴ , ∴ .
随堂练习
4、 已知函数
(1)求此函数的定义域,值域.
(2)确定函数的单调区间.
【解析】
(1)定义域为R,
∵ ,
∴ ,
∴ 函数的值域为.
随堂练习
(2)令 ,
则 .
∵ ,∴ 为减函数,
又∵ 在上单调递减,在上单调递增.
∴ 函数的单调递增区间为,单调递减区间为.
谢谢观看
人教A版
高中数学 · 必修一
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
