2022—2023学年人教版数学八年级下册17.1 勾股定理 基础习题(无答案)
文档属性
| 名称 | 2022—2023学年人教版数学八年级下册17.1 勾股定理 基础习题(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 230.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
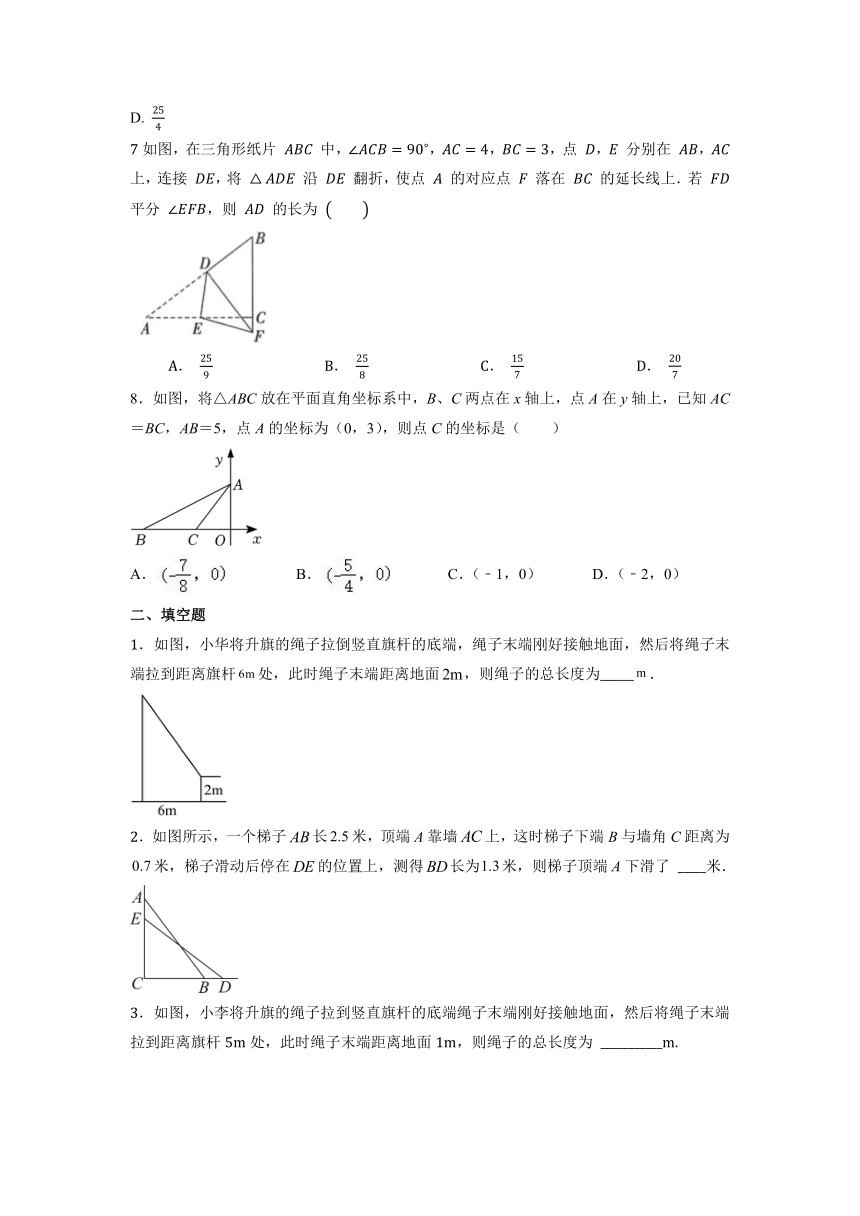
| 科目 | 数学 | ||
| 更新时间 | 2023-03-06 18:04:50 | ||
图片预览

文档简介
17.1 勾股定理
一、选择题
1、下列数据中,哪一组不是勾股数( )
A. 7,24,25 B. 9,40,41 C. 3,4,5 D. 8,15,19
2. 如图,所有阴影四边形都是正方形,所有三角形都是直角三角形,已知正方形,,的面积依次为,,,则正方形的面积为( )
A. B. C. D.
3如图所示,某人到岛上去探宝,从 处登陆后先往北走 ,又往东走 ,再向北走 ,往西一拐,仅走 就找到宝藏.问登陆点 与宝藏埋藏点 之间的距离是
A. B. C. D.
4.直角三角形三边的长分别为3、4、x,则x可能取的值为( )
A.5 B.6或 C.5或 D.
5. 如图,直线上有三个正方形,,,若,的面积分别为和,则的面积为( )
A. B. C. D.
6. 如图,在中,,线段的垂直平分线交于点,交于点若,,则的长为( )
A.
B.
C.
D.
7如图,在三角形纸片 中,,,,点 , 分别在 , 上,连接 ,将 沿 翻折,使点 的对应点 落在 的延长线上.若 平分 ,则 的长为
A. B. C. D.
8.如图,将△ABC放在平面直角坐标系中,B、C两点在x轴上,点A在y轴上,已知AC=BC,AB=5,点A的坐标为(0,3),则点C的坐标是( )
A. B. C.(﹣1,0) D.(﹣2,0)
二、填空题
1.如图,小华将升旗的绳子拉倒竖直旗杆的底端,绳子末端刚好接触地面,然后将绳子末端拉到距离旗杆处,此时绳子末端距离地面,则绳子的总长度为______.
2.如图所示,一个梯子长米,顶端A靠墙上,这时梯子下端B与墙角C距离为米,梯子滑动后停在的位置上,测得长为米,则梯子顶端A下滑了 _____米.
3.如图,小李将升旗的绳子拉到竖直旗杆的底端绳子末端刚好接触地面,然后将绳子末端拉到距离旗杆5m处,此时绳子末端距离地面1m,则绳子的总长度为 ___________m.
4.如图,有两棵树,一棵高8m,另一棵高2m,两树相距8m,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少要飞______m.
5.如图,一根竹子高尺(尺=米),折断后竹子顶端落在离竹子底端尺处,则折断处离地面的高度是_____尺.
三、解答题
1.如图有一个四级台阶,它的每一级的长、宽分别为18分米、4分米.
(1)如果给台阶表面8个矩形区域铺上定制红毯,需要定制红毯的面积为432平方分米,那么每一级台阶的高为多少分米?
(2)A和C是这个台阶上两个相对的端点,台阶角落点A处有一只蚂蚁,想到台阶顶端点C处去吃美味的食物,则蚂蚁沿着台阶面从点A爬行到点C的最短路程为多少分米?
2.如图,在△ABC中,∠ACB=90°,CD⊥AB于D,,AB=5,求BC、CD的长.
3.勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,当两个全等的直角三角形如图摆放时,可以用“面积法”来证明.将两个全等的直角三角形按如图所示摆放,使点A、E、D在同一条直线上.利用此图的面积表示式证明勾股定理.
4.如图所示,一架梯子 AB 斜靠在墙面上,且 AB 的长为 2.5m.
(1)若梯子底端离墙角的距离 OB 为 1.5m,求这个梯子的顶端 A 距地面有多高?
(2)在(1)的条件下,如果梯子的顶端 A 下滑 0.5m 到点 A,那么梯子的底端 B 在水平方向滑动的距离 BB` 为多少米?
5.如图,A,B两个村庄在河CD的同侧,两村庄的距离为a千米,,它们到河CD的距离分别是1千米和3千米.为了解决这两个村庄的饮水问题,乡政府决定在河CD边上修建一水厂向A,B两村输送水.
(1)在图上作出向A,B两村铺设水管所用材料最省时的水厂位置M.(只需作图,不需要证明)
(2)经预算,修建水厂需20万元,铺设水管的所有费用平均每千米为3万元,其他费用需5万元,求完成这项工程乡政府投入的资金至少为多少万元。
一、选择题
1、下列数据中,哪一组不是勾股数( )
A. 7,24,25 B. 9,40,41 C. 3,4,5 D. 8,15,19
2. 如图,所有阴影四边形都是正方形,所有三角形都是直角三角形,已知正方形,,的面积依次为,,,则正方形的面积为( )
A. B. C. D.
3如图所示,某人到岛上去探宝,从 处登陆后先往北走 ,又往东走 ,再向北走 ,往西一拐,仅走 就找到宝藏.问登陆点 与宝藏埋藏点 之间的距离是
A. B. C. D.
4.直角三角形三边的长分别为3、4、x,则x可能取的值为( )
A.5 B.6或 C.5或 D.
5. 如图,直线上有三个正方形,,,若,的面积分别为和,则的面积为( )
A. B. C. D.
6. 如图,在中,,线段的垂直平分线交于点,交于点若,,则的长为( )
A.
B.
C.
D.
7如图,在三角形纸片 中,,,,点 , 分别在 , 上,连接 ,将 沿 翻折,使点 的对应点 落在 的延长线上.若 平分 ,则 的长为
A. B. C. D.
8.如图,将△ABC放在平面直角坐标系中,B、C两点在x轴上,点A在y轴上,已知AC=BC,AB=5,点A的坐标为(0,3),则点C的坐标是( )
A. B. C.(﹣1,0) D.(﹣2,0)
二、填空题
1.如图,小华将升旗的绳子拉倒竖直旗杆的底端,绳子末端刚好接触地面,然后将绳子末端拉到距离旗杆处,此时绳子末端距离地面,则绳子的总长度为______.
2.如图所示,一个梯子长米,顶端A靠墙上,这时梯子下端B与墙角C距离为米,梯子滑动后停在的位置上,测得长为米,则梯子顶端A下滑了 _____米.
3.如图,小李将升旗的绳子拉到竖直旗杆的底端绳子末端刚好接触地面,然后将绳子末端拉到距离旗杆5m处,此时绳子末端距离地面1m,则绳子的总长度为 ___________m.
4.如图,有两棵树,一棵高8m,另一棵高2m,两树相距8m,一只小鸟从一棵树的树梢飞到另一棵树的树梢,至少要飞______m.
5.如图,一根竹子高尺(尺=米),折断后竹子顶端落在离竹子底端尺处,则折断处离地面的高度是_____尺.
三、解答题
1.如图有一个四级台阶,它的每一级的长、宽分别为18分米、4分米.
(1)如果给台阶表面8个矩形区域铺上定制红毯,需要定制红毯的面积为432平方分米,那么每一级台阶的高为多少分米?
(2)A和C是这个台阶上两个相对的端点,台阶角落点A处有一只蚂蚁,想到台阶顶端点C处去吃美味的食物,则蚂蚁沿着台阶面从点A爬行到点C的最短路程为多少分米?
2.如图,在△ABC中,∠ACB=90°,CD⊥AB于D,,AB=5,求BC、CD的长.
3.勾股定理神秘而美妙,它的证法多样,其巧妙各有不同,当两个全等的直角三角形如图摆放时,可以用“面积法”来证明.将两个全等的直角三角形按如图所示摆放,使点A、E、D在同一条直线上.利用此图的面积表示式证明勾股定理.
4.如图所示,一架梯子 AB 斜靠在墙面上,且 AB 的长为 2.5m.
(1)若梯子底端离墙角的距离 OB 为 1.5m,求这个梯子的顶端 A 距地面有多高?
(2)在(1)的条件下,如果梯子的顶端 A 下滑 0.5m 到点 A,那么梯子的底端 B 在水平方向滑动的距离 BB` 为多少米?
5.如图,A,B两个村庄在河CD的同侧,两村庄的距离为a千米,,它们到河CD的距离分别是1千米和3千米.为了解决这两个村庄的饮水问题,乡政府决定在河CD边上修建一水厂向A,B两村输送水.
(1)在图上作出向A,B两村铺设水管所用材料最省时的水厂位置M.(只需作图,不需要证明)
(2)经预算,修建水厂需20万元,铺设水管的所有费用平均每千米为3万元,其他费用需5万元,求完成这项工程乡政府投入的资金至少为多少万元。
