第8章 一元一次不等式(培优篇)-2022-2023学年七年级数学下册阶段性复习精选精练(华东师大版)
文档属性
| 名称 | 第8章 一元一次不等式(培优篇)-2022-2023学年七年级数学下册阶段性复习精选精练(华东师大版) |  | |
| 格式 | docx | ||
| 文件大小 | 477.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-05 21:05:48 | ||
图片预览




文档简介
第8章 一元一次不等式(培优篇)
一、单选题(本大题共10小题,每小题3分,共30分)
1.如果,那么下列不等式成立的是( )
A. B.
C. D.
2.一元一次不等式3(7﹣x)≥1+x的正整数解有( )
A.3个 B.4个 C.5个 D.6个
3.数轴上、、三点依次从左向右排列,表示的数分别为-2,,,则可能是( )
A.0 B.-1 C.-2 D.3
4.已知a、b是不为0的实数,则下列选项中,解集可以为的不等式组是( )
A. B. C. D.
5.小红购买了一本《数学和数学家的故事》·两位小伙伴想知道书的价格,小红让他们猜,小华说:“不少于20元”,小强说:“少于22元”,小红说:“你们两个人说的都没有错”,则这本书的价格(元)所在的范围为( )
A. B. C. D.
6.如图,在数轴上A,B,C,D四个点所对应的数中是不等式组的解的是( )
A.点A对应的数 B.点B对应的数
C.点C对应的数 D.点D对应的数
7.如图所示,运行程序规定:从“输入一个值”到“结果是否”为一次程序操作,如果程序操作进行了三次才停止,那么的取值范围是( )
A. B. C. D.
8.若数使关于的不等式的最小正整数解是,则的取值范围是( )
A. B. C. D.
9.若关于x的一元一次不等式组的解集是xa,且关于y的分式方程有非负整数解,则符合条件的所有整数a的和为( )
A.0 B.1 C.4 D.6
10.已知关于x、y的方程组,给出下列说法:
①当a =1时,方程组的解也是方程x+y=2的一个解;②当x-2y>8时,;③不论a取什么实数,2x+y的值始终不变;④若,则. 以上说法正确的是( )
A.②③④ B.①②④ C.③④ D.②③
填空题(本大题共8小题,每小题4分,共32分)
11.已知关于x的不等式的解也是不等式的解,则常数a的取值范围是_____.
12.已知实数x,y满足x+y=3,且x>﹣3,y≥1,则x﹣y的取值范围____.
13.已知不等式组的解集为,则m的取值范围是________.
14.若关于x的不等式组,恰有两个整数解,则m的取值范围是______.
15.关于x的不等式组无整数解,则a的取值范围为_____.
16.不等式组的解集为,则的取值范围为_____.
17.已知a、b、c是非负数,且2a+3b+c=10,a+b-c=4,如果S=2a+b-2c,那么S的最大值和最小值的和等于_________.
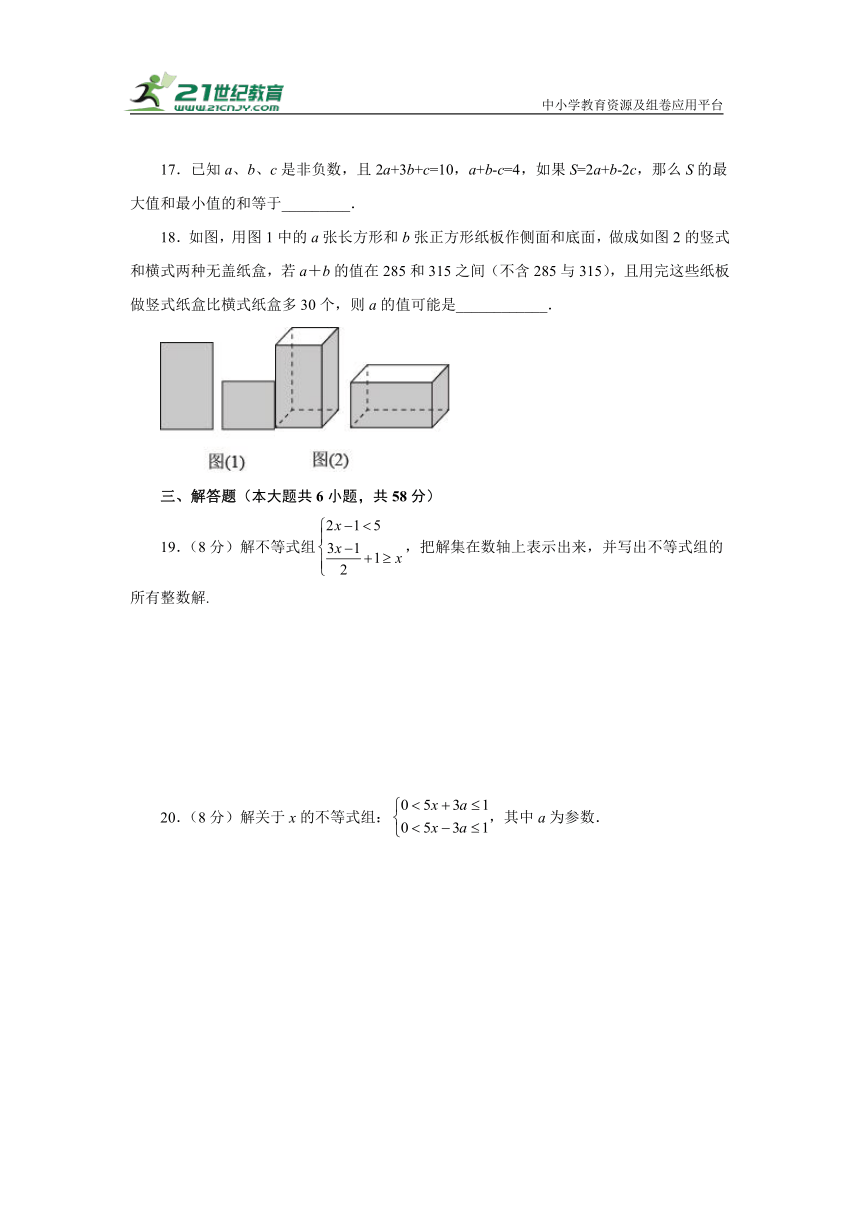
18.如图,用图1中的a张长方形和b张正方形纸板作侧面和底面,做成如图2的竖式和横式两种无盖纸盒,若a+b的值在285和315之间(不含285与315),且用完这些纸板做竖式纸盒比横式纸盒多30个,则a的值可能是____________.
三、解答题(本大题共6小题,共58分)
19.(8分)解不等式组,把解集在数轴上表示出来,并写出不等式组的所有整数解.
20.(8分)解关于x的不等式组:,其中a为参数.
21.(10分)现有不等式的两个性质:①在不等式的两边都加上(或减去)同一个数(或整式),不等号的方向不变.②在不等式的两边都乘同一个数(或整式),乘的数(或整式)为正时不等号的方向不变,乘的数(或整式)为负时不等号的方向改变.
请解决以下两个问题:
利用性质①比较2a 与a 的大小(a≠0).
利用性质②比较2a 与a 的大小(a≠0).
22.(10分)若任意一个代数式,在给定的范围内求得的最大值和最小值恰好也在该范围内,则称这个代数式是这个范围的“湘一代数式”.例如:关于x的代数式,当1x 1时,代数式在x1时有最大值,最大值为1;在x0时有最小值,最小值为0,此时最值1,0均在1x1这个范围内,则称代数式是1x1的“湘一代数式”.
(1)若关于的代数式,当时,取得的最大值为 ,最小值为 ,所以代数式 (填“是”或“不是”)的“湘一代数式”.
(2)若关于的代数式是的“湘一代数式”,求a的最大值与最小值.
(3)若关于的代数式是的“湘一代数式”,求m的取值范围.
23.(10分)为支援武汉抗击新冠肺炎,甲地捐赠了600吨的救援物质并联系了一家快递公司进行运送.快递公司准备安排A、B两种车型把这批物资从甲地快速送到武汉.其中,从甲地到武汉,A型货车5辆、B型货车6辆,一共需补贴油费3800元;A型货车3辆、B型货车2辆,一共需补贴油费1800元.
(1)从甲地到武汉,A、B两种型号的货车,每辆车需补贴的油费分别是多少元?
(2)A型货车每辆可装15吨物资,B型货车每辆可装12吨物资,安排的B型货车的数量是A型货车的2倍还多4辆,且A型车最多可安排18辆、运送这批物资,不同安排中,补贴的总的油费最少是多少?
24.(12分)老王是新农村建设中涌现出的“养殖专业户”.他准备购置80只相同规格的网箱,养殖A、B两种淡水鱼(两种鱼不能混养).计划用于养鱼的总投资不少于7万元,但不超过7.2万元,其中购置网箱等基础建设需要1.2万元.设他用x只网箱养殖A种淡水鱼,目前平均每只网箱养殖A、B两种淡水鱼所需投入及产出情况如表:
鱼苗投资 (百元) 饲料支出 (百元) 收获成品鱼 (千克) 成品鱼价格 (百元/千克)
A种鱼 2 3 100 0.1
B种鱼 4 5 55 0.4
(利润=收入-支出.收入指成品鱼收益,支出包括基础建设投入、鱼苗投资及饲料支出)
(1)按目前市场行情,老王养殖A、B两种淡水鱼获得利润最多是多少万元?
(2)基础建设投入、鱼苗投资、饲料支出及产量不变,但当老王的鱼上市时,A种鱼价格上涨a%,B种鱼价格下降20%,使老王养鱼实际获得利润5.68万元.求a的值.
参考答案
1.D
【分析】根据不等式的性质即可求出答案.
解:∵,
∴,
∵,
∴,
故选D.
【点拨】本题考查不等式的性质,解题的关键是熟练运用不等式的性质,本题属于中等题型.
2.C
【分析】先求出不等式的解集,根据解集得出答案即可.
解:
∴
所以不等式的正整数解为1,2,3,4,5,共5个,
故选:C.
【点拨】本题考查了解一元一次不等式,不等式的正整数解的应用,能求出不等式的解集是解此题的关键.
3.A
【分析】根据条件列出关于的一元一次不等式组,解得的范围,即可求得答案.
解:由题意知,
,解得.
故选:A.
【点拨】本题主要考查列一元一次不等式以及解一元一次不等式组,解决本题的关键是列出一元一次不等式组.
4.D
【分析】根据解集可以为,所以a、b异号,分两种情况:当a>0,b<0时,则;当a<0,b>0时,则;分别逐项判定即可.
解:∵解集可以为,
∴a、b异号,
当a>0,b<0时,则,
A、的解集为x<,故此选项不符合题意;
B、的无解,故此选项不符合题意;
C、的解集为x>,故此选项不符合题意;
D、的解集为当a<0,b>0时,则,
A、的解集为x>,故此选项不符合题意;
B、的无解,故此选项不符合题意;
C、的解集为x<,故此选项不符合题意;
D、的解集为综上,a、b是不为0的实数,解集可以为的不等式组是D,
故选:D.
【点拨】本题考查不等式组的解集,解不等式组,熟练掌握不等式组解集的确定原则“大大取较大,小小取较小,大小小大中间找,大大小小无处找”是解题的关键.
5.C
【分析】根据不少于就是大于等于的意思去建立不等式即可.
解:∵书的价格“不少于20元”,“少于22元”,
∴,
故选C.
【点拨】本题考查了列不等式,正确理解不少于的意义是解题的关键.
6.B
【分析】先求出不等式组的解集,然后判断即可得出答案.
解:
解不等式①,得,
解不等式②,得,
∴不等式组的解为,
∴在数轴上B点所对应的数是不等式组的解.
故选∶B.
【点拨】本题考查了解不等式组和数轴上点的特征,正确求出不等式组的解集是解题的关键.
7.C
【分析】根据运算程序,前两次运算结果小于等于79,第三次运算结果大于79列出不等式组,然后求解即可.
解:由题意得,
,
解不等式①得,x≤39,
解不等式②得,x≤19,
解不等式③得,x>9,
所以,x的取值范围是9<x≤19.
故选:C.
【点拨】本题考查了一元一次不等式组的应用,读懂题目信息,理解运输程序并列出不等式组是解题的关键.
8.D
【分析】由不等式的最小正整数解为,可得出关于a的一元一次不等式,解之即可得出a的取值范围.
解:∵关于的不等式的最小正整数解是
∴
故选:D.
【点拨】此题主要考查一元一次不等式的正整数解的问题,熟练利用数轴理解一元一次不等式的解集是解题的关键.
9.B
【分析】先解关于x的一元一次不等式组,根据其解集,求出的取值范围,再解分式方程,根据其有非负整数解,求出的取值范围,进而可得符合要求的值,最后求和即可.
解:由不等式组,解得:
∵不等式组的解集为
∴
由分式方程 ,去分母得
解得,
∵分式方程有非负数解
∴且
∴的取值为,0,1,2,4
∴符合条件的所有整数a的和为
故选B.
【点拨】本题考查了解一元一次不等式组,解分式方程.解题的关键在于求出符合条件的所有整数a.
10.A
解:试题分析:当a=1时,方程x+y=1-a=0,因此方程组的解不是x+y=2的解,故①不正确;通过加减消元法可解方程组为x=3+a,y=-2a-2,代入x-2y>8可解得a>,故②正确;2x+y=6+2a+(-2a-2)=4,故③正确;代入x、y的值可得-2a-2=(3+a)2+5,化简整理可得a=-4,故④正确.
故选:A
11.
【分析】先把a看作常数求出两个不等式的解集,再根据同小取小列出不等式求解即可.
解:关于x的不等式,
解得:,
关于x的不等式的解也是不等式的解,
,
不等式的解集是,
,解得:,
,
,
故答案为:.
【点拨】本题考查了一元一次不等式的解法,解题的关键是分别求出两个不等式的解集,再根据同小取小列出关于a的不等式,注意在不等式两边都除以一个负数时,应只改变不等号的方向.
12.
【分析】先设x﹣y=m,利用x+y=3,构造方程组,求出用m表示x、y的代数式,再根据x>﹣3,y≥1,列不等式求出m的范围即可.
解:设x﹣y=m,
∴,
②+①得,
②-①得,
∵y≥1,
∴,
解得,
∵x>﹣3,
∴,
解得,
∴,
x﹣y的取值范围.
故答案为.
【点拨】本题考查方程与不等式综合问题,解题关键是设出x﹣y=m,与x+y=3,构造方程组从中求出,,再出列不等式.
13.
【分析】求出每个不等式的解集,根据已知得出关于m的不等式,求出不等式的解集即可.
解:
解①得,,
解②得,,
不等式组的解集为,
,
,
故答案为:.
【点拨】本题考查了解一元一次不等式组的应用,解题的关键是能根据不等式的解集和已知得出关于m的不等式.
14.
【分析】不等式组整理后表示出解集,根据不等式组恰有两个整数解,确定出m的范围即可.
解:
解不等式①得,,
解不等式②得,,
∴不等式解集为:,
∵不等式组恰有两个整数解,即-1,0,
∴0≤<1,
解得:.
故答案为:.
【点拨】此题考查了一元一次不等式组的整数解,以及解一元一次不等式组,熟练掌握不等式组的解法是解本题的关键.
15.a≥2.
【分析】先求出两个不等式的解集,再根据不等式组无整数解列出关于a的不等式求解即可
解:不等式组整理得:
不等式组的解集是:a<x<,
当a≥时,不等式组无解,
∵不等式组无整数解,
∴a≥2
故答案为:a≥2.
【点拨】本题考查了一元一次不等式组的解法,解题的关键是熟练掌握确定不等式组解集的方法.
16.k≥1
解:解不等式2x+9>6x+1可得x<2,解不等式x-k<1,可得x<k+1,由于x<2,可知k+1≥2,解得k≥1.
故答案为k≥1.
17.14
【分析】把a看成是已知数,分别用含a的式子表示b,c,根据a,b,c是非负数求出a的范围,把b,c代入S=2a+b-2c,根据a的范围求出S的最大值和最小值.
解:由方程组得,,
因为a,b,c是非负数,所以,解得2≤a≤.
S=2a+b-2c=2a+-2×,
当a=2时,S==6;
当a=时,S==8.
则6+8=14.
故答案为14.
【点拨】三个未知数,两个方程的问题,通常将其中的一个未知数看成是已知数,用这个字母表示出其它两个未知数,再根据题意,确定这个未知数的取值范围.
18.218,225,232
【分析】根据题意图形可知,竖式纸盒需要4个长方形纸板与1个正方形纸板,横式纸盒要3个长方形纸板与2个正方形纸板,设做成横式纸盒x个,则做成竖式纸盒个,即可算出总共用的纸板数,再根据,即可得到不等式组求出x的值,即可进行求解.
解:设做成横式纸盒x个,则做成竖式纸盒个,
∵,
∴,
解得,
∵x为正整数,
∴或或,
当时,,
,
当时,,
,
当时,,
,
综上所述,a的值为218,225,232,
故答案为:218,225,232.
【点拨】此题主要考查不等式的应用,解题的关键是根据题意设出未知数,找到不等关系进行求解,注意结合实际情况取整数解.
19.,数轴上表示略,不等式组的所有整数解为-1,0,1,2
【分析】先求出两个不等式的解集,再求其公共解集,然后确定这个范围内的整数解即可.
解:由①得:,
由②得:,解得:,
解集为:.
不等式组的所有整数解为-1,0,1,2.
【点拨】本题主要考查了一元一次不等式组解集的求法,把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),在表示解集时“≥”,“≤”要用实心圆点表示;<”,“>”要用空心圆点表示.
20.见分析
【分析】求出不等式组中每个不等式的解集,分别求出当时、当时、当时、当时a的值,结合不等式的解集,即可求出在各段的不等式组的解集.
解:
解不等式①得:,
,
解不等式②得:,
,
∵当时,a=0,
当时,a=0,
当时,
当时,,
∴当 或时,原不等式组无解;
当时,原不等式组的解集为
当时,原不等式组的解集为:.
【点拨】本题考查了不等式组得解集,关键是能正确求出各段的不等式组的解集,本题比较特殊,有一定的难度.
21.(1)2a试题分析:(1)根据不等式的性质①,可得答案;
(2)根据不等式的性质②,可得答案.
解:(1)当a>0时,a+a>a+0,即2a>a.
当a<0时,a+a<a+0,即2a<a.
(2)当a>0时,由2>1,得2·a>1·a,即2a>a.
当a<0时,由2>1,得2·a<1·a,即2a<a.
22.(1)是.(2)a的最大值为,最小值为;(3)
【分析】(1)先求解当时,的最大值与最小值,再根据定义判断即可;
(2)当时,得分 <,分别求解在内时的最大值与最小值,再列不等式组即可得到答案;
(3)当时,分,两种情况分别求解的最大值与最小值,再列不等式(组)求解即可.
解:(1)
当时,取最大值,
当时,取最小值
所以代数式是的“湘一代数式”.
故答案为:是.
(2)∵,
∴0≤|x|≤2,
∴
①当a≥0时,x=0时, 有最大值为,
x=2或-2时,有最小值为
所以可得不等式组,
由①得:
由②得:
所以:
②a<0时,x=0时, 有最小值为,
x=2或-2时, 的有大值为
所以可得不等式组,
由①得:
由②得:
所以:<,
综上①②可得,
所以a的最大值为,最小值为.
(3) 是的“湘一代数式”,
当时,的最大值是 最小值是
当时,
当时,取最小值
当时,取最大值,
解得:
综上:的取值范围是:
【点拨】本题考查的是新定义情境下的不等式或不等式组的应用,理解定义列不等式(组)是解题的关键.
23.(1)每辆A型货车补贴油费400元,每辆B型货车补贴油费300元;(2)16200元
【分析】(1)设从甲地到武汉,每辆A型货车补贴油费x元,每辆B型货车补贴油费y元,根据“从甲地到武汉,A型货车5辆、B型货车6辆,一共需补贴油费3800元;A型货车3辆、B型货车2辆,一共需补贴油费1800元”,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)设安排A型货车m辆,则安排B型货车(2m+4)辆,根据A型车最多可安排18辆且安排的车辆总的装载量不低于600吨,即可得出关于m的一元一次不等式组,解之即可得出m的取值范围,结合m为整数即可得出m的值,再求出各安排方案所需补贴的总的油费,比较后即可得出结论.
解:(1)设从甲地到武汉,每辆A型货车补贴油费x元,每辆B型货车补贴油费y元,依题意,得:
解得:
答:从甲地到武汉,每辆A型货车补贴油费400元,每辆B型货车补贴油费300元.
(2)设安排A型货车m辆,则安排B型货车()辆,依题意,得:
解得:
∵m为正整数
∴15,16,17,18
当时,补贴的总的油费为(元)
当时,补贴的总的油费为(元);
当时,补贴的总的油费为(元);
当时,补贴的总的油费为(元)
∵
∴运送这批物资,不同安排中,补贴的总的油费最少是16200元.
【点拨】本题考查了二元一次方程组的应用以及一元一次不等式组的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)根据各数量之间的关系,正确列出一元一次不等式组.
24.(1)6.8万元;(2)36.
试题分析:(1)根据题意求出30≤x≤35,再表示出A、B两种鱼所获利润,最后找最大利润;(2)表示出价格变动后,A、B两种鱼上市时所获利润,再解方程.
解:(1)设他用x只网箱养殖A种淡水鱼,则用(80-x)只网箱养殖B种淡水鱼.
由题意,得700≤5x+9(80﹣x)+120≤720,
解得:30≤x≤35
设A、B两种鱼所获利润w="(10-5)x+(22-9)×(80-x)-120=-8x+920,"
所以,当x=30时,所获利润w最多是6.8万元
(2)价格变动后,一箱A种鱼的利润=100×0.1×(1+a%)﹣(2+3)=5+0.1a(百元),
一箱B种鱼的利润=55×0.4×(1﹣20%)﹣(4+5)=8.6(百元).
设A、B两种鱼上市时所获利润w="(5+0.1a)x+8.6×(80-x)-120=(0.1a-3.6)x+568,"
所以,(0.1a-3.6)x+568=568,所以,(0.1a-3.6)x=0
因为,30≤x≤35,所以,0.1a-3.6=0,a=36.
中小学教育资源及组卷应用平台
考点:一元一次不等式组.
一、单选题(本大题共10小题,每小题3分,共30分)
1.如果,那么下列不等式成立的是( )
A. B.
C. D.
2.一元一次不等式3(7﹣x)≥1+x的正整数解有( )
A.3个 B.4个 C.5个 D.6个
3.数轴上、、三点依次从左向右排列,表示的数分别为-2,,,则可能是( )
A.0 B.-1 C.-2 D.3
4.已知a、b是不为0的实数,则下列选项中,解集可以为的不等式组是( )
A. B. C. D.
5.小红购买了一本《数学和数学家的故事》·两位小伙伴想知道书的价格,小红让他们猜,小华说:“不少于20元”,小强说:“少于22元”,小红说:“你们两个人说的都没有错”,则这本书的价格(元)所在的范围为( )
A. B. C. D.
6.如图,在数轴上A,B,C,D四个点所对应的数中是不等式组的解的是( )
A.点A对应的数 B.点B对应的数
C.点C对应的数 D.点D对应的数
7.如图所示,运行程序规定:从“输入一个值”到“结果是否”为一次程序操作,如果程序操作进行了三次才停止,那么的取值范围是( )
A. B. C. D.
8.若数使关于的不等式的最小正整数解是,则的取值范围是( )
A. B. C. D.
9.若关于x的一元一次不等式组的解集是xa,且关于y的分式方程有非负整数解,则符合条件的所有整数a的和为( )
A.0 B.1 C.4 D.6
10.已知关于x、y的方程组,给出下列说法:
①当a =1时,方程组的解也是方程x+y=2的一个解;②当x-2y>8时,;③不论a取什么实数,2x+y的值始终不变;④若,则. 以上说法正确的是( )
A.②③④ B.①②④ C.③④ D.②③
填空题(本大题共8小题,每小题4分,共32分)
11.已知关于x的不等式的解也是不等式的解,则常数a的取值范围是_____.
12.已知实数x,y满足x+y=3,且x>﹣3,y≥1,则x﹣y的取值范围____.
13.已知不等式组的解集为,则m的取值范围是________.
14.若关于x的不等式组,恰有两个整数解,则m的取值范围是______.
15.关于x的不等式组无整数解,则a的取值范围为_____.
16.不等式组的解集为,则的取值范围为_____.
17.已知a、b、c是非负数,且2a+3b+c=10,a+b-c=4,如果S=2a+b-2c,那么S的最大值和最小值的和等于_________.
18.如图,用图1中的a张长方形和b张正方形纸板作侧面和底面,做成如图2的竖式和横式两种无盖纸盒,若a+b的值在285和315之间(不含285与315),且用完这些纸板做竖式纸盒比横式纸盒多30个,则a的值可能是____________.
三、解答题(本大题共6小题,共58分)
19.(8分)解不等式组,把解集在数轴上表示出来,并写出不等式组的所有整数解.
20.(8分)解关于x的不等式组:,其中a为参数.
21.(10分)现有不等式的两个性质:①在不等式的两边都加上(或减去)同一个数(或整式),不等号的方向不变.②在不等式的两边都乘同一个数(或整式),乘的数(或整式)为正时不等号的方向不变,乘的数(或整式)为负时不等号的方向改变.
请解决以下两个问题:
利用性质①比较2a 与a 的大小(a≠0).
利用性质②比较2a 与a 的大小(a≠0).
22.(10分)若任意一个代数式,在给定的范围内求得的最大值和最小值恰好也在该范围内,则称这个代数式是这个范围的“湘一代数式”.例如:关于x的代数式,当1x 1时,代数式在x1时有最大值,最大值为1;在x0时有最小值,最小值为0,此时最值1,0均在1x1这个范围内,则称代数式是1x1的“湘一代数式”.
(1)若关于的代数式,当时,取得的最大值为 ,最小值为 ,所以代数式 (填“是”或“不是”)的“湘一代数式”.
(2)若关于的代数式是的“湘一代数式”,求a的最大值与最小值.
(3)若关于的代数式是的“湘一代数式”,求m的取值范围.
23.(10分)为支援武汉抗击新冠肺炎,甲地捐赠了600吨的救援物质并联系了一家快递公司进行运送.快递公司准备安排A、B两种车型把这批物资从甲地快速送到武汉.其中,从甲地到武汉,A型货车5辆、B型货车6辆,一共需补贴油费3800元;A型货车3辆、B型货车2辆,一共需补贴油费1800元.
(1)从甲地到武汉,A、B两种型号的货车,每辆车需补贴的油费分别是多少元?
(2)A型货车每辆可装15吨物资,B型货车每辆可装12吨物资,安排的B型货车的数量是A型货车的2倍还多4辆,且A型车最多可安排18辆、运送这批物资,不同安排中,补贴的总的油费最少是多少?
24.(12分)老王是新农村建设中涌现出的“养殖专业户”.他准备购置80只相同规格的网箱,养殖A、B两种淡水鱼(两种鱼不能混养).计划用于养鱼的总投资不少于7万元,但不超过7.2万元,其中购置网箱等基础建设需要1.2万元.设他用x只网箱养殖A种淡水鱼,目前平均每只网箱养殖A、B两种淡水鱼所需投入及产出情况如表:
鱼苗投资 (百元) 饲料支出 (百元) 收获成品鱼 (千克) 成品鱼价格 (百元/千克)
A种鱼 2 3 100 0.1
B种鱼 4 5 55 0.4
(利润=收入-支出.收入指成品鱼收益,支出包括基础建设投入、鱼苗投资及饲料支出)
(1)按目前市场行情,老王养殖A、B两种淡水鱼获得利润最多是多少万元?
(2)基础建设投入、鱼苗投资、饲料支出及产量不变,但当老王的鱼上市时,A种鱼价格上涨a%,B种鱼价格下降20%,使老王养鱼实际获得利润5.68万元.求a的值.
参考答案
1.D
【分析】根据不等式的性质即可求出答案.
解:∵,
∴,
∵,
∴,
故选D.
【点拨】本题考查不等式的性质,解题的关键是熟练运用不等式的性质,本题属于中等题型.
2.C
【分析】先求出不等式的解集,根据解集得出答案即可.
解:
∴
所以不等式的正整数解为1,2,3,4,5,共5个,
故选:C.
【点拨】本题考查了解一元一次不等式,不等式的正整数解的应用,能求出不等式的解集是解此题的关键.
3.A
【分析】根据条件列出关于的一元一次不等式组,解得的范围,即可求得答案.
解:由题意知,
,解得.
故选:A.
【点拨】本题主要考查列一元一次不等式以及解一元一次不等式组,解决本题的关键是列出一元一次不等式组.
4.D
【分析】根据解集可以为,所以a、b异号,分两种情况:当a>0,b<0时,则;当a<0,b>0时,则;分别逐项判定即可.
解:∵解集可以为,
∴a、b异号,
当a>0,b<0时,则,
A、的解集为x<,故此选项不符合题意;
B、的无解,故此选项不符合题意;
C、的解集为x>,故此选项不符合题意;
D、的解集为
A、的解集为x>,故此选项不符合题意;
B、的无解,故此选项不符合题意;
C、的解集为x<,故此选项不符合题意;
D、的解集为
故选:D.
【点拨】本题考查不等式组的解集,解不等式组,熟练掌握不等式组解集的确定原则“大大取较大,小小取较小,大小小大中间找,大大小小无处找”是解题的关键.
5.C
【分析】根据不少于就是大于等于的意思去建立不等式即可.
解:∵书的价格“不少于20元”,“少于22元”,
∴,
故选C.
【点拨】本题考查了列不等式,正确理解不少于的意义是解题的关键.
6.B
【分析】先求出不等式组的解集,然后判断即可得出答案.
解:
解不等式①,得,
解不等式②,得,
∴不等式组的解为,
∴在数轴上B点所对应的数是不等式组的解.
故选∶B.
【点拨】本题考查了解不等式组和数轴上点的特征,正确求出不等式组的解集是解题的关键.
7.C
【分析】根据运算程序,前两次运算结果小于等于79,第三次运算结果大于79列出不等式组,然后求解即可.
解:由题意得,
,
解不等式①得,x≤39,
解不等式②得,x≤19,
解不等式③得,x>9,
所以,x的取值范围是9<x≤19.
故选:C.
【点拨】本题考查了一元一次不等式组的应用,读懂题目信息,理解运输程序并列出不等式组是解题的关键.
8.D
【分析】由不等式的最小正整数解为,可得出关于a的一元一次不等式,解之即可得出a的取值范围.
解:∵关于的不等式的最小正整数解是
∴
故选:D.
【点拨】此题主要考查一元一次不等式的正整数解的问题,熟练利用数轴理解一元一次不等式的解集是解题的关键.
9.B
【分析】先解关于x的一元一次不等式组,根据其解集,求出的取值范围,再解分式方程,根据其有非负整数解,求出的取值范围,进而可得符合要求的值,最后求和即可.
解:由不等式组,解得:
∵不等式组的解集为
∴
由分式方程 ,去分母得
解得,
∵分式方程有非负数解
∴且
∴的取值为,0,1,2,4
∴符合条件的所有整数a的和为
故选B.
【点拨】本题考查了解一元一次不等式组,解分式方程.解题的关键在于求出符合条件的所有整数a.
10.A
解:试题分析:当a=1时,方程x+y=1-a=0,因此方程组的解不是x+y=2的解,故①不正确;通过加减消元法可解方程组为x=3+a,y=-2a-2,代入x-2y>8可解得a>,故②正确;2x+y=6+2a+(-2a-2)=4,故③正确;代入x、y的值可得-2a-2=(3+a)2+5,化简整理可得a=-4,故④正确.
故选:A
11.
【分析】先把a看作常数求出两个不等式的解集,再根据同小取小列出不等式求解即可.
解:关于x的不等式,
解得:,
关于x的不等式的解也是不等式的解,
,
不等式的解集是,
,解得:,
,
,
故答案为:.
【点拨】本题考查了一元一次不等式的解法,解题的关键是分别求出两个不等式的解集,再根据同小取小列出关于a的不等式,注意在不等式两边都除以一个负数时,应只改变不等号的方向.
12.
【分析】先设x﹣y=m,利用x+y=3,构造方程组,求出用m表示x、y的代数式,再根据x>﹣3,y≥1,列不等式求出m的范围即可.
解:设x﹣y=m,
∴,
②+①得,
②-①得,
∵y≥1,
∴,
解得,
∵x>﹣3,
∴,
解得,
∴,
x﹣y的取值范围.
故答案为.
【点拨】本题考查方程与不等式综合问题,解题关键是设出x﹣y=m,与x+y=3,构造方程组从中求出,,再出列不等式.
13.
【分析】求出每个不等式的解集,根据已知得出关于m的不等式,求出不等式的解集即可.
解:
解①得,,
解②得,,
不等式组的解集为,
,
,
故答案为:.
【点拨】本题考查了解一元一次不等式组的应用,解题的关键是能根据不等式的解集和已知得出关于m的不等式.
14.
【分析】不等式组整理后表示出解集,根据不等式组恰有两个整数解,确定出m的范围即可.
解:
解不等式①得,,
解不等式②得,,
∴不等式解集为:,
∵不等式组恰有两个整数解,即-1,0,
∴0≤<1,
解得:.
故答案为:.
【点拨】此题考查了一元一次不等式组的整数解,以及解一元一次不等式组,熟练掌握不等式组的解法是解本题的关键.
15.a≥2.
【分析】先求出两个不等式的解集,再根据不等式组无整数解列出关于a的不等式求解即可
解:不等式组整理得:
不等式组的解集是:a<x<,
当a≥时,不等式组无解,
∵不等式组无整数解,
∴a≥2
故答案为:a≥2.
【点拨】本题考查了一元一次不等式组的解法,解题的关键是熟练掌握确定不等式组解集的方法.
16.k≥1
解:解不等式2x+9>6x+1可得x<2,解不等式x-k<1,可得x<k+1,由于x<2,可知k+1≥2,解得k≥1.
故答案为k≥1.
17.14
【分析】把a看成是已知数,分别用含a的式子表示b,c,根据a,b,c是非负数求出a的范围,把b,c代入S=2a+b-2c,根据a的范围求出S的最大值和最小值.
解:由方程组得,,
因为a,b,c是非负数,所以,解得2≤a≤.
S=2a+b-2c=2a+-2×,
当a=2时,S==6;
当a=时,S==8.
则6+8=14.
故答案为14.
【点拨】三个未知数,两个方程的问题,通常将其中的一个未知数看成是已知数,用这个字母表示出其它两个未知数,再根据题意,确定这个未知数的取值范围.
18.218,225,232
【分析】根据题意图形可知,竖式纸盒需要4个长方形纸板与1个正方形纸板,横式纸盒要3个长方形纸板与2个正方形纸板,设做成横式纸盒x个,则做成竖式纸盒个,即可算出总共用的纸板数,再根据,即可得到不等式组求出x的值,即可进行求解.
解:设做成横式纸盒x个,则做成竖式纸盒个,
∵,
∴,
解得,
∵x为正整数,
∴或或,
当时,,
,
当时,,
,
当时,,
,
综上所述,a的值为218,225,232,
故答案为:218,225,232.
【点拨】此题主要考查不等式的应用,解题的关键是根据题意设出未知数,找到不等关系进行求解,注意结合实际情况取整数解.
19.,数轴上表示略,不等式组的所有整数解为-1,0,1,2
【分析】先求出两个不等式的解集,再求其公共解集,然后确定这个范围内的整数解即可.
解:由①得:,
由②得:,解得:,
解集为:.
不等式组的所有整数解为-1,0,1,2.
【点拨】本题主要考查了一元一次不等式组解集的求法,把每个不等式的解集在数轴上表示出来(>,≥向右画;<,≤向左画),在表示解集时“≥”,“≤”要用实心圆点表示;<”,“>”要用空心圆点表示.
20.见分析
【分析】求出不等式组中每个不等式的解集,分别求出当时、当时、当时、当时a的值,结合不等式的解集,即可求出在各段的不等式组的解集.
解:
解不等式①得:,
,
解不等式②得:,
,
∵当时,a=0,
当时,a=0,
当时,
当时,,
∴当 或时,原不等式组无解;
当时,原不等式组的解集为
当时,原不等式组的解集为:.
【点拨】本题考查了不等式组得解集,关键是能正确求出各段的不等式组的解集,本题比较特殊,有一定的难度.
21.(1)2a
(2)根据不等式的性质②,可得答案.
解:(1)当a>0时,a+a>a+0,即2a>a.
当a<0时,a+a<a+0,即2a<a.
(2)当a>0时,由2>1,得2·a>1·a,即2a>a.
当a<0时,由2>1,得2·a<1·a,即2a<a.
22.(1)是.(2)a的最大值为,最小值为;(3)
【分析】(1)先求解当时,的最大值与最小值,再根据定义判断即可;
(2)当时,得分 <,分别求解在内时的最大值与最小值,再列不等式组即可得到答案;
(3)当时,分,两种情况分别求解的最大值与最小值,再列不等式(组)求解即可.
解:(1)
当时,取最大值,
当时,取最小值
所以代数式是的“湘一代数式”.
故答案为:是.
(2)∵,
∴0≤|x|≤2,
∴
①当a≥0时,x=0时, 有最大值为,
x=2或-2时,有最小值为
所以可得不等式组,
由①得:
由②得:
所以:
②a<0时,x=0时, 有最小值为,
x=2或-2时, 的有大值为
所以可得不等式组,
由①得:
由②得:
所以:<,
综上①②可得,
所以a的最大值为,最小值为.
(3) 是的“湘一代数式”,
当时,的最大值是 最小值是
当时,
当时,取最小值
当时,取最大值,
解得:
综上:的取值范围是:
【点拨】本题考查的是新定义情境下的不等式或不等式组的应用,理解定义列不等式(组)是解题的关键.
23.(1)每辆A型货车补贴油费400元,每辆B型货车补贴油费300元;(2)16200元
【分析】(1)设从甲地到武汉,每辆A型货车补贴油费x元,每辆B型货车补贴油费y元,根据“从甲地到武汉,A型货车5辆、B型货车6辆,一共需补贴油费3800元;A型货车3辆、B型货车2辆,一共需补贴油费1800元”,即可得出关于x,y的二元一次方程组,解之即可得出结论;
(2)设安排A型货车m辆,则安排B型货车(2m+4)辆,根据A型车最多可安排18辆且安排的车辆总的装载量不低于600吨,即可得出关于m的一元一次不等式组,解之即可得出m的取值范围,结合m为整数即可得出m的值,再求出各安排方案所需补贴的总的油费,比较后即可得出结论.
解:(1)设从甲地到武汉,每辆A型货车补贴油费x元,每辆B型货车补贴油费y元,依题意,得:
解得:
答:从甲地到武汉,每辆A型货车补贴油费400元,每辆B型货车补贴油费300元.
(2)设安排A型货车m辆,则安排B型货车()辆,依题意,得:
解得:
∵m为正整数
∴15,16,17,18
当时,补贴的总的油费为(元)
当时,补贴的总的油费为(元);
当时,补贴的总的油费为(元);
当时,补贴的总的油费为(元)
∵
∴运送这批物资,不同安排中,补贴的总的油费最少是16200元.
【点拨】本题考查了二元一次方程组的应用以及一元一次不等式组的应用,解题的关键是:(1)找准等量关系,正确列出二元一次方程组;(2)根据各数量之间的关系,正确列出一元一次不等式组.
24.(1)6.8万元;(2)36.
试题分析:(1)根据题意求出30≤x≤35,再表示出A、B两种鱼所获利润,最后找最大利润;(2)表示出价格变动后,A、B两种鱼上市时所获利润,再解方程.
解:(1)设他用x只网箱养殖A种淡水鱼,则用(80-x)只网箱养殖B种淡水鱼.
由题意,得700≤5x+9(80﹣x)+120≤720,
解得:30≤x≤35
设A、B两种鱼所获利润w="(10-5)x+(22-9)×(80-x)-120=-8x+920,"
所以,当x=30时,所获利润w最多是6.8万元
(2)价格变动后,一箱A种鱼的利润=100×0.1×(1+a%)﹣(2+3)=5+0.1a(百元),
一箱B种鱼的利润=55×0.4×(1﹣20%)﹣(4+5)=8.6(百元).
设A、B两种鱼上市时所获利润w="(5+0.1a)x+8.6×(80-x)-120=(0.1a-3.6)x+568,"
所以,(0.1a-3.6)x+568=568,所以,(0.1a-3.6)x=0
因为,30≤x≤35,所以,0.1a-3.6=0,a=36.
中小学教育资源及组卷应用平台
考点:一元一次不等式组.
