2022—2023学年人教版数学九年级上册 25.3用频率估计概率(1)课件(共23张PPT)
文档属性
| 名称 | 2022—2023学年人教版数学九年级上册 25.3用频率估计概率(1)课件(共23张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 505.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-07 07:44:13 | ||
图片预览








文档简介
(共23张PPT)
概率伴随着我你他
★用列举法求概率的条件是:
(1)实验的结果是有限个(n)
(2)各种结果的可能性相等.
知识回顾
问题(两题中任选一题):
2.掷一次骰子,向上的一面数字是6的概率是___.
1.某射击运动员射击一次,命中靶心的概率是___.
等可能事件
命中靶心与未命中靶心发生可能性不相等.
试验的结果不是有限个的非等可能情形,比如种子发芽,扔瓶盖,投篮命中率等非等可能情形下概率又如何计算呢?
25.3 用频率估计概率
新人教版九年级上册第二十五章
在实验中,每个对象出现的次数称为频数.
频率=
频数:
频率:
所考察对象出现的次数与实验的总次数的比叫做频率.
做抛硬币的实验:
当抛一枚硬币时会出现几种结果?_____
其中正面朝上的概率是多少?_________
无论抛多少次,正面朝上的概率会不会改变?______
若抛10次,其中4次正面朝上,则正面朝上的频率是多少?_________
如果有5次正面向上呢?_____
频率是否会改变?__________
这就是说同次试验的频率和概率是否相同?
2种
0.5
不变
0.4
0.5
会改变
有时相同,有时不相同
完成下列填空
活动目的:
抛掷一枚硬币,判断其正面向上的可能性
有多大?
活动方式:
全体同学每人抛硬币10次(硬币自备),
老师负责统计正面向上次数并填表.
观察数据:
“正面向上”的频率有什么规律?
试验:抛硬币
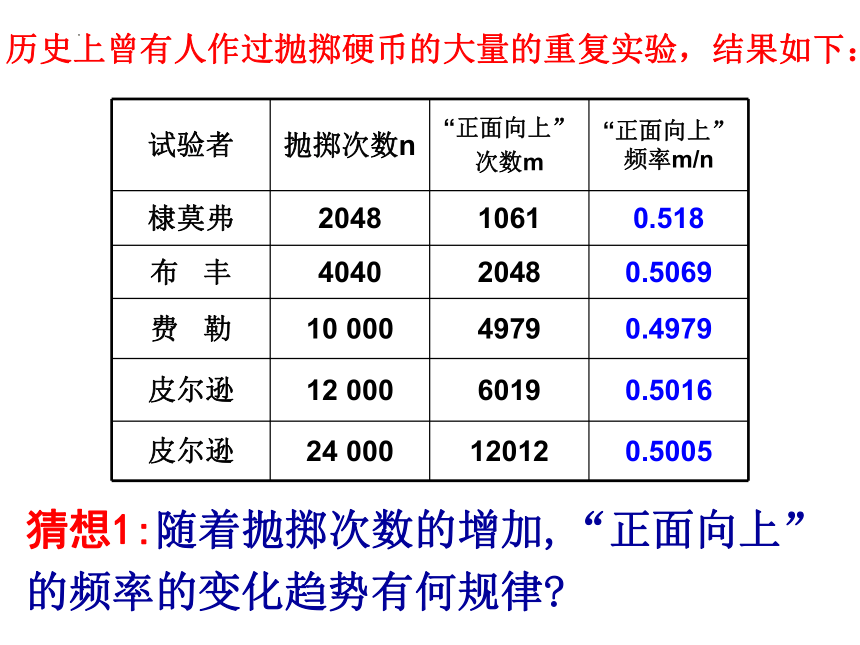
试验者 抛掷次数n “正面向上” 次数m “正面向上”频率m/n
棣莫弗 2048 1061 0.518
布 丰 4040 2048 0.5069
费 勒 10 000 4979 0.4979
皮尔逊 12 000 6019 0.5016
皮尔逊 24 000 12012 0.5005
猜想1:随着抛掷次数的增加,“正面向上”
的频率的变化趋势有何规律
历史上曾有人作过抛掷硬币的大量的重复实验,结果如下:
观察发现:
抛掷次数n
频率m/n
0.5
1
2048
4040
12000
24000
30000
72088
“正面向上”的频率在0.5 附近摆动.
随着抛掷次数的增加,频率呈现出稳定性:
在0.5左右摆动的幅度会越来越小---我们称
“正面向上”的频率稳定于0.5
试验:抛硬币
“反面向上”的频率也相应的稳定于0.5
猜想2:
当“正面向上”的频率稳定于0.5时,
“反面向上”的频率呈现什么规律?
思考:
“若连续2次抛掷一枚质地均匀的硬币,
那么一定是1次正面朝上,1次反面朝上”.
这个说法对吗?
试验:抛硬币
抛掷一枚硬币出现正面的概率为0.5,是
大量试验得出的一种规律性结果,对具体的
几次试验来讲不一定能体现出这种规律性.
大量试验
抛硬币的试验告诉我们:
但要求:试验次数n足够大,频率才能估计概率!
我们用列举法得出“正面向上”的概率,
与用频率的稳定性得出的概率,是同一个
数值!
一般地,即使试验的所有可能结果
不是有限个,或各种结果发生的可能性
不相等,我们也可通过试验的方法,用
频率估计一个随机事件的概率.
数学史实
人们在长期的实践中发现,在随机试验中,
由于众多微小的偶然因素的影响,每次测得的
结果虽不尽相同,但大量重复试验所得结果却
能反应客观规律.
由频率可以估计概率是由瑞士数学家雅各布·伯努利(1654-
1705)最早阐明的,因而他被公认为是概率论的先驱之一.
频率稳定性定理
随机事件在一次试验中是否
发生虽然不能事先确定,但是在
大量重复试验的情况下,它的发
生呈现出一定的规律性.出现的频率值接近于常数.
事件A的概率的定义:
一般地,在大量重复试验中,如果
事件A发生的频率 会稳定在某个常
数 p附近,那么这个常数 p叫做事件A的概率.
记为P(A)=p 或 P(A)=
归纳
由定义可知:
(1)求一个事件的概率的基本方法是通过大量的重复试验;
(3)概率是频率的稳定值,而频率是概率的近似值;
(4)概率反映了随机事件发生的可能性的大小;
(5)必然事件的概率为1,不可能事件的概率为0.因此 .
(2)只有当频率在某个常数附近摆动时,这个常数才叫做事件A 的概率;
1. 抛硬币时“正面向上”的概率是0.5,
某人连掷硬币100次,结果一定是正面
向上50次,反面向上50次吗?
巩固:
2.据报道:我国1998年的洪水是“百
年一遇”的大洪水,在这里“百年一遇”
是什么意思?
巩固:
3.天气预报说某天降水概率为90%,
而这天并未降水.你能从概率的角度
作出解释吗?
巩固:
从上面可知,概率是通过大量重复试验中
频率的稳定性得到的一个0--1的常数,它反映了
事件发生的可能性的大小. 需要注意,概率是针对大量试验而言的,大量试验反映的规律并非在每次试验中一定存在.
特别说明:
投篮次数(n) 50 100 150 200 250 300 500
投中次数(m) 28 60 78 104 123 152 251
投中频率( )
下表记录了一名球员在罚球线上的投篮结果.
(1)计算表中的投中频率(精确到0.01);
(2)这个球员投篮一次,投中的概率大约是多少?
(精确到0.1)
0.56
0.60
0.52
0.52
0.50
0.51
0.50
约为0.5
思考练习:
课堂小结
了解了一种方法-----用多次试验频率去估计概率
弄清了一种关系------频率与概率的关系
当试验次数很多或试验时样本容量足够大时,一件事件发生的频率与相应的概率会非常接近.此时,我们可以用一件事件发生的频率来估计这一事件发生的概率.
谈谈你在这节课中的收获!
概率伴随着我你他
★用列举法求概率的条件是:
(1)实验的结果是有限个(n)
(2)各种结果的可能性相等.
知识回顾
问题(两题中任选一题):
2.掷一次骰子,向上的一面数字是6的概率是___.
1.某射击运动员射击一次,命中靶心的概率是___.
等可能事件
命中靶心与未命中靶心发生可能性不相等.
试验的结果不是有限个的非等可能情形,比如种子发芽,扔瓶盖,投篮命中率等非等可能情形下概率又如何计算呢?
25.3 用频率估计概率
新人教版九年级上册第二十五章
在实验中,每个对象出现的次数称为频数.
频率=
频数:
频率:
所考察对象出现的次数与实验的总次数的比叫做频率.
做抛硬币的实验:
当抛一枚硬币时会出现几种结果?_____
其中正面朝上的概率是多少?_________
无论抛多少次,正面朝上的概率会不会改变?______
若抛10次,其中4次正面朝上,则正面朝上的频率是多少?_________
如果有5次正面向上呢?_____
频率是否会改变?__________
这就是说同次试验的频率和概率是否相同?
2种
0.5
不变
0.4
0.5
会改变
有时相同,有时不相同
完成下列填空
活动目的:
抛掷一枚硬币,判断其正面向上的可能性
有多大?
活动方式:
全体同学每人抛硬币10次(硬币自备),
老师负责统计正面向上次数并填表.
观察数据:
“正面向上”的频率有什么规律?
试验:抛硬币
试验者 抛掷次数n “正面向上” 次数m “正面向上”频率m/n
棣莫弗 2048 1061 0.518
布 丰 4040 2048 0.5069
费 勒 10 000 4979 0.4979
皮尔逊 12 000 6019 0.5016
皮尔逊 24 000 12012 0.5005
猜想1:随着抛掷次数的增加,“正面向上”
的频率的变化趋势有何规律
历史上曾有人作过抛掷硬币的大量的重复实验,结果如下:
观察发现:
抛掷次数n
频率m/n
0.5
1
2048
4040
12000
24000
30000
72088
“正面向上”的频率在0.5 附近摆动.
随着抛掷次数的增加,频率呈现出稳定性:
在0.5左右摆动的幅度会越来越小---我们称
“正面向上”的频率稳定于0.5
试验:抛硬币
“反面向上”的频率也相应的稳定于0.5
猜想2:
当“正面向上”的频率稳定于0.5时,
“反面向上”的频率呈现什么规律?
思考:
“若连续2次抛掷一枚质地均匀的硬币,
那么一定是1次正面朝上,1次反面朝上”.
这个说法对吗?
试验:抛硬币
抛掷一枚硬币出现正面的概率为0.5,是
大量试验得出的一种规律性结果,对具体的
几次试验来讲不一定能体现出这种规律性.
大量试验
抛硬币的试验告诉我们:
但要求:试验次数n足够大,频率才能估计概率!
我们用列举法得出“正面向上”的概率,
与用频率的稳定性得出的概率,是同一个
数值!
一般地,即使试验的所有可能结果
不是有限个,或各种结果发生的可能性
不相等,我们也可通过试验的方法,用
频率估计一个随机事件的概率.
数学史实
人们在长期的实践中发现,在随机试验中,
由于众多微小的偶然因素的影响,每次测得的
结果虽不尽相同,但大量重复试验所得结果却
能反应客观规律.
由频率可以估计概率是由瑞士数学家雅各布·伯努利(1654-
1705)最早阐明的,因而他被公认为是概率论的先驱之一.
频率稳定性定理
随机事件在一次试验中是否
发生虽然不能事先确定,但是在
大量重复试验的情况下,它的发
生呈现出一定的规律性.出现的频率值接近于常数.
事件A的概率的定义:
一般地,在大量重复试验中,如果
事件A发生的频率 会稳定在某个常
数 p附近,那么这个常数 p叫做事件A的概率.
记为P(A)=p 或 P(A)=
归纳
由定义可知:
(1)求一个事件的概率的基本方法是通过大量的重复试验;
(3)概率是频率的稳定值,而频率是概率的近似值;
(4)概率反映了随机事件发生的可能性的大小;
(5)必然事件的概率为1,不可能事件的概率为0.因此 .
(2)只有当频率在某个常数附近摆动时,这个常数才叫做事件A 的概率;
1. 抛硬币时“正面向上”的概率是0.5,
某人连掷硬币100次,结果一定是正面
向上50次,反面向上50次吗?
巩固:
2.据报道:我国1998年的洪水是“百
年一遇”的大洪水,在这里“百年一遇”
是什么意思?
巩固:
3.天气预报说某天降水概率为90%,
而这天并未降水.你能从概率的角度
作出解释吗?
巩固:
从上面可知,概率是通过大量重复试验中
频率的稳定性得到的一个0--1的常数,它反映了
事件发生的可能性的大小. 需要注意,概率是针对大量试验而言的,大量试验反映的规律并非在每次试验中一定存在.
特别说明:
投篮次数(n) 50 100 150 200 250 300 500
投中次数(m) 28 60 78 104 123 152 251
投中频率( )
下表记录了一名球员在罚球线上的投篮结果.
(1)计算表中的投中频率(精确到0.01);
(2)这个球员投篮一次,投中的概率大约是多少?
(精确到0.1)
0.56
0.60
0.52
0.52
0.50
0.51
0.50
约为0.5
思考练习:
课堂小结
了解了一种方法-----用多次试验频率去估计概率
弄清了一种关系------频率与概率的关系
当试验次数很多或试验时样本容量足够大时,一件事件发生的频率与相应的概率会非常接近.此时,我们可以用一件事件发生的频率来估计这一事件发生的概率.
谈谈你在这节课中的收获!
同课章节目录
