合情推理课件
图片预览









文档简介
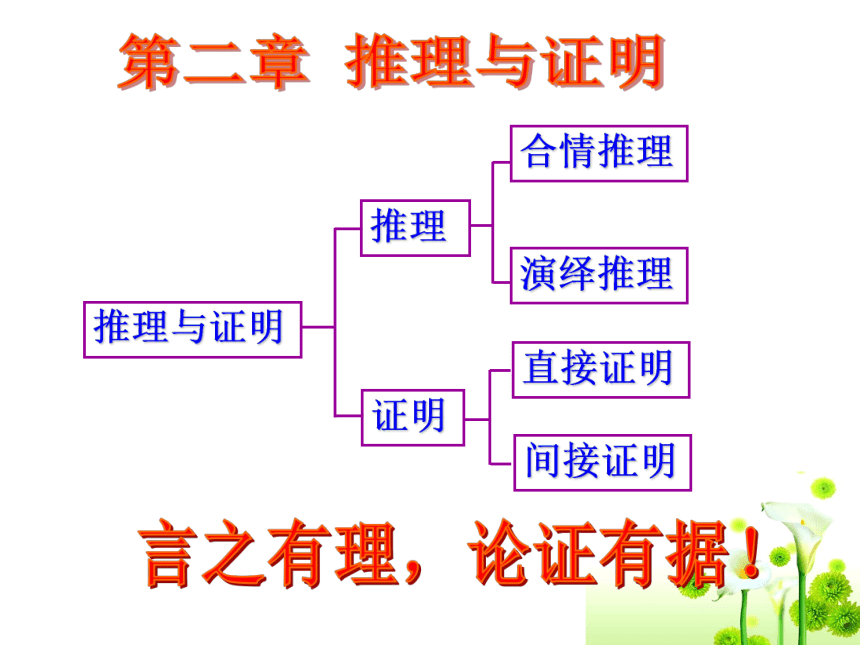
课件43张PPT。2.1.1合情推理已知的判断新的判断 根据一个或几个已知的判断来确定一个新的判断的思维过程就叫推理.推理与证明推理证明言之有理,论证有据!第二章 推理与证明2.1.1合情推理(1)几个著名的猜想:歌德巴赫猜想费马猜想地图的”四色猜想”歌尼斯堡七桥猜想黎曼猜想卡拉比猜想费马猜想每幅地图都可以用四种颜色着色,使得有共同边界的国家着上不同的颜色。 地图的”四色猜想”歌尼斯堡七桥猜想18世纪在哥尼斯堡城(今俄罗斯加里宁格勒)的普莱格尔河上有7座桥,将河中的两个岛和河岸连结,如图所示。城中的居民经常沿河过桥散步,于是提出了一个问题:能否一次走遍7座桥,而每座桥只许通过一次,最后仍回到起始地点。??????????????????????????????????10= 3+7
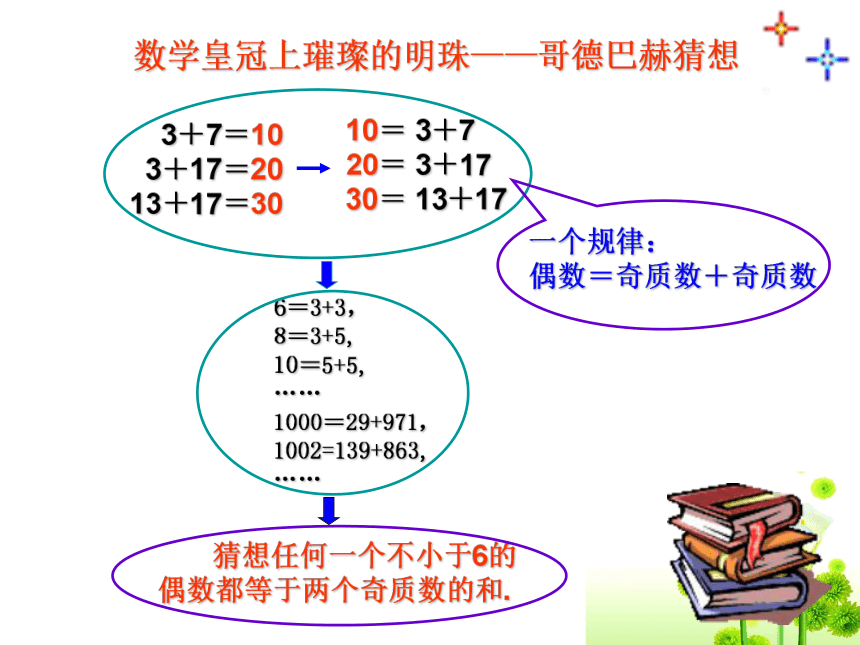
20= 3+17
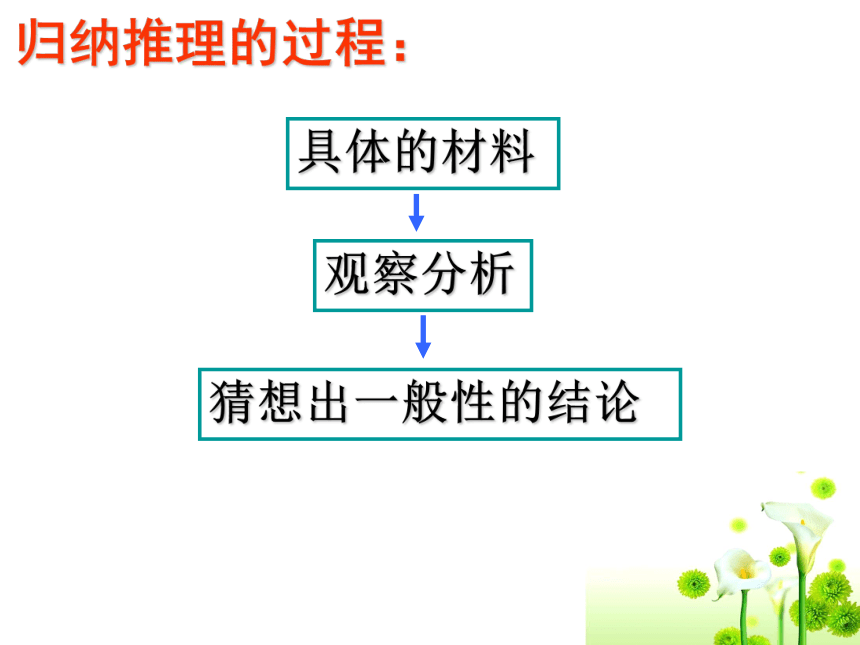
30= 13+17数学皇冠上璀璨的明珠——哥德巴赫猜想哥德巴赫猜想的过程:归纳推理的过程: 由某类事物的 具有某些特征,
推出该类事物的 都具有这些特征
的推理,或者由 概括出
的推理,称为归纳推理(简称归纳).部分对象全部对象个别事实一般结论归纳推理 1,3,5,7,…,由此你猜想出第
个数是_______.这就是从部分到整体,从个别到一般的归纳推理.你想起来了吗?统计初步中的用样本估计总体 通过从总体中抽取部分对象进
行观测或试验,进而对整体做出推断. 意思是从一片树叶的凋落,知道秋
天将要来到.比喻由细微的迹象看出整体
形势的变化,由部分推知全体. 1.已知数列{ }的第一项 =1,
且 ( =1,2,3,···),
请归纳出这个数列的通项公式为________.让我们一起来归纳推理(2004春季上海)根据图中5个图形及相应点的个数的变化规律,试猜测第n个图形中有 个点.(1)(2)(3)(4)(5)练习2.如图所示,有三根针和套在一根针上的若干金属片.按下列规则,把金属片从一根针上全部移到另一根针上.
(1)每次只能移动1个金属片;
(2)较大的金属片不能放在较小的金属片上面;
试推测:把n个金属片从1号针移到3号针,最少需要移动多少次?123让我们一起来归纳推理123第1个圆环从1到3.设 为把 个圆环从1号针移到3号针的最少次数,则 =1时, =2时,123前1个圆环从1到2;
第2个圆环从1到3;
第1个圆环从2到3.第1个圆环从1到3.设 为把 个圆环从1号针移到3号针的最少次数,则 =1时, n=3时,前2个圆环从1到2;
第3个圆环从1到3;
前2个圆环从2到3. =2时,前1个圆环从1到2;
第2个圆环从1到3;
第1个圆环从2到3.第1个圆环从1到3.设 为把 个圆环从1号针移到3号针的最少次数,则 =1时,123猜想 an=2n -13.(05年广东)设平面内有n条直线(n≥3),其中有且仅有两条直线互相平行,任意三条直线不过同一点.若用f(n)表示这n条直线交点的个数.当n ≥3 时, f(n)= .(用n表示)让我们一起来归纳推理归纳推理的基础归纳推理的作用归纳推理观察、分析发现新事实、获得新结论由部分到整体、
个别到一般的推理归纳推理的结论不一定成立在创造发明中,
人们经常应用
类比可能有生命存在有生命存在温度适合生物的生存一年中有四季的变更有大气层行星、围绕太阳运行、绕轴自转火星地球火星上是否存在生命火星与地球类比的思维过程:火星地球存在类似特征 由两类对象具有某些类似特征和其中
一类对象的某些已知特征,推出另一类对
象也具有这些特征的推理称为类比推理.类比推理1、进行类比推理的步骤: (1)找出两类对象之间可以确切表述的相似特征;(2)用一类对象的已知特征去猜测另一类对象的特征,从而得出一个猜想;
(3)检验这个猜想.2、类比推理的一般模式:所以B类事物可能具有性质d’.A类事物具有性质a,b,c,d,B类事物具有性质a’,b’,c’,(a,b,c与a’,b’,c’相似或相同)观察、比较联想、类推猜想新结论我们已经学习过“等差数列”与“等比数列”.你是否想过“等和数列”、“等积数列” ? 从第二项起,每一项与其前一项的差等于一个常数的数列是等差数列. 从第二项起,每一项与其前一项的和等于一个常数的数列是等和数列.例1.试根据等式的性质猜想不等式的性质。等式的性质:
(1) a=b?a+c=b+c;
(2) a=b? ac=bc;
(3) a=b?a2=b2; 猜想不等式的性质:(1) a>b?a+c>b+c;(2) a>b? ac>bc;(3) a>b?a2>b2;类比推理的结论不一定成立.让我们一起来类比推理例2 类比实数的加法和乘法,列出它们相似的运算性质.若a,b∈R,则ab∈Rab=ba
(ab)c=a(bc)乘法的逆运算是除法,使得ax=1有唯一解x=1/aa·1=a例3.试将平面上的圆与空间的球进行类比圆的定义:平面内到一个定点的距离等于定长的点的集合.球的定义:到一个定点的距离等于定长的点的集合.圆
弦
直径周长
面积球
截面圆大圆表面积体积球心与截面圆(不经过球心的截面圆)
圆心连线垂直于截面圆.与球心距离相等的两截面圆面积相等;与球心距离不等的两截面圆面积不等,距球心较近的截面圆面积较大.以点P(x0,y0,z0)为球心,r为半径的球的方程为
(x-x0)2+(y-y0)2+(z-z0)2=r2.例题4:类比平面内直角三角形的勾股定理,试给出空间中四面体性质的猜想。3个面两两垂直的四面体∠PDF=∠PDE=∠EDF=90°
三个两两垂直的面S1,S2,S3和
1个“斜面” S?c2=a2+b2分析:△PEF的面积为S下面证明猜想是否成立:过D点作DM⊥EF,垂足为M,连接PM,则PM⊥EF 变式练习:在三角形ABC中有结论:AB+BC>AC,类似地在四面体P-ABC中有 .PS1S2S3△PAB的面积为S图(1)图(2)类比推理类比推理
以旧的知识为基础,推测新的结果,具有发现的功能
由特殊到特殊的推理类比推理的结论不一定成立类比推理由特殊到特殊的推理;以旧的知识为基础,推测新的结果;结论不一定成立.归纳推理由部分到整体、特殊到一般的推理;以观察分析为基础,推测新的结论;具有发现的功能;结论不一定成立.具有发现的功能;归纳推理和类比推理的过程通俗地说,合情推理是指“合乎情理”的推理.几何中常见的类比对象三角形四面体(各面均为三角形)四边形六面体(各面均为四边形)圆球代数中常见的类比对象数 向量方程函数不等式交集,并集,补集或,且,非运算无限有限
20= 3+17
30= 13+17数学皇冠上璀璨的明珠——哥德巴赫猜想哥德巴赫猜想的过程:归纳推理的过程: 由某类事物的 具有某些特征,
推出该类事物的 都具有这些特征
的推理,或者由 概括出
的推理,称为归纳推理(简称归纳).部分对象全部对象个别事实一般结论归纳推理 1,3,5,7,…,由此你猜想出第
个数是_______.这就是从部分到整体,从个别到一般的归纳推理.你想起来了吗?统计初步中的用样本估计总体 通过从总体中抽取部分对象进
行观测或试验,进而对整体做出推断. 意思是从一片树叶的凋落,知道秋
天将要来到.比喻由细微的迹象看出整体
形势的变化,由部分推知全体. 1.已知数列{ }的第一项 =1,
且 ( =1,2,3,···),
请归纳出这个数列的通项公式为________.让我们一起来归纳推理(2004春季上海)根据图中5个图形及相应点的个数的变化规律,试猜测第n个图形中有 个点.(1)(2)(3)(4)(5)练习2.如图所示,有三根针和套在一根针上的若干金属片.按下列规则,把金属片从一根针上全部移到另一根针上.
(1)每次只能移动1个金属片;
(2)较大的金属片不能放在较小的金属片上面;
试推测:把n个金属片从1号针移到3号针,最少需要移动多少次?123让我们一起来归纳推理123第1个圆环从1到3.设 为把 个圆环从1号针移到3号针的最少次数,则 =1时, =2时,123前1个圆环从1到2;
第2个圆环从1到3;
第1个圆环从2到3.第1个圆环从1到3.设 为把 个圆环从1号针移到3号针的最少次数,则 =1时, n=3时,前2个圆环从1到2;
第3个圆环从1到3;
前2个圆环从2到3. =2时,前1个圆环从1到2;
第2个圆环从1到3;
第1个圆环从2到3.第1个圆环从1到3.设 为把 个圆环从1号针移到3号针的最少次数,则 =1时,123猜想 an=2n -13.(05年广东)设平面内有n条直线(n≥3),其中有且仅有两条直线互相平行,任意三条直线不过同一点.若用f(n)表示这n条直线交点的个数.当n ≥3 时, f(n)= .(用n表示)让我们一起来归纳推理归纳推理的基础归纳推理的作用归纳推理观察、分析发现新事实、获得新结论由部分到整体、
个别到一般的推理归纳推理的结论不一定成立在创造发明中,
人们经常应用
类比可能有生命存在有生命存在温度适合生物的生存一年中有四季的变更有大气层行星、围绕太阳运行、绕轴自转火星地球火星上是否存在生命火星与地球类比的思维过程:火星地球存在类似特征 由两类对象具有某些类似特征和其中
一类对象的某些已知特征,推出另一类对
象也具有这些特征的推理称为类比推理.类比推理1、进行类比推理的步骤: (1)找出两类对象之间可以确切表述的相似特征;(2)用一类对象的已知特征去猜测另一类对象的特征,从而得出一个猜想;
(3)检验这个猜想.2、类比推理的一般模式:所以B类事物可能具有性质d’.A类事物具有性质a,b,c,d,B类事物具有性质a’,b’,c’,(a,b,c与a’,b’,c’相似或相同)观察、比较联想、类推猜想新结论我们已经学习过“等差数列”与“等比数列”.你是否想过“等和数列”、“等积数列” ? 从第二项起,每一项与其前一项的差等于一个常数的数列是等差数列. 从第二项起,每一项与其前一项的和等于一个常数的数列是等和数列.例1.试根据等式的性质猜想不等式的性质。等式的性质:
(1) a=b?a+c=b+c;
(2) a=b? ac=bc;
(3) a=b?a2=b2; 猜想不等式的性质:(1) a>b?a+c>b+c;(2) a>b? ac>bc;(3) a>b?a2>b2;类比推理的结论不一定成立.让我们一起来类比推理例2 类比实数的加法和乘法,列出它们相似的运算性质.若a,b∈R,则ab∈Rab=ba
(ab)c=a(bc)乘法的逆运算是除法,使得ax=1有唯一解x=1/aa·1=a例3.试将平面上的圆与空间的球进行类比圆的定义:平面内到一个定点的距离等于定长的点的集合.球的定义:到一个定点的距离等于定长的点的集合.圆
弦
直径周长
面积球
截面圆大圆表面积体积球心与截面圆(不经过球心的截面圆)
圆心连线垂直于截面圆.与球心距离相等的两截面圆面积相等;与球心距离不等的两截面圆面积不等,距球心较近的截面圆面积较大.以点P(x0,y0,z0)为球心,r为半径的球的方程为
(x-x0)2+(y-y0)2+(z-z0)2=r2.例题4:类比平面内直角三角形的勾股定理,试给出空间中四面体性质的猜想。3个面两两垂直的四面体∠PDF=∠PDE=∠EDF=90°
三个两两垂直的面S1,S2,S3和
1个“斜面” S?c2=a2+b2分析:△PEF的面积为S下面证明猜想是否成立:过D点作DM⊥EF,垂足为M,连接PM,则PM⊥EF 变式练习:在三角形ABC中有结论:AB+BC>AC,类似地在四面体P-ABC中有 .PS1S2S3△PAB的面积为S图(1)图(2)类比推理类比推理
以旧的知识为基础,推测新的结果,具有发现的功能
由特殊到特殊的推理类比推理的结论不一定成立类比推理由特殊到特殊的推理;以旧的知识为基础,推测新的结果;结论不一定成立.归纳推理由部分到整体、特殊到一般的推理;以观察分析为基础,推测新的结论;具有发现的功能;结论不一定成立.具有发现的功能;归纳推理和类比推理的过程通俗地说,合情推理是指“合乎情理”的推理.几何中常见的类比对象三角形四面体(各面均为三角形)四边形六面体(各面均为四边形)圆球代数中常见的类比对象数 向量方程函数不等式交集,并集,补集或,且,非运算无限有限
