单调性与最大小值课件

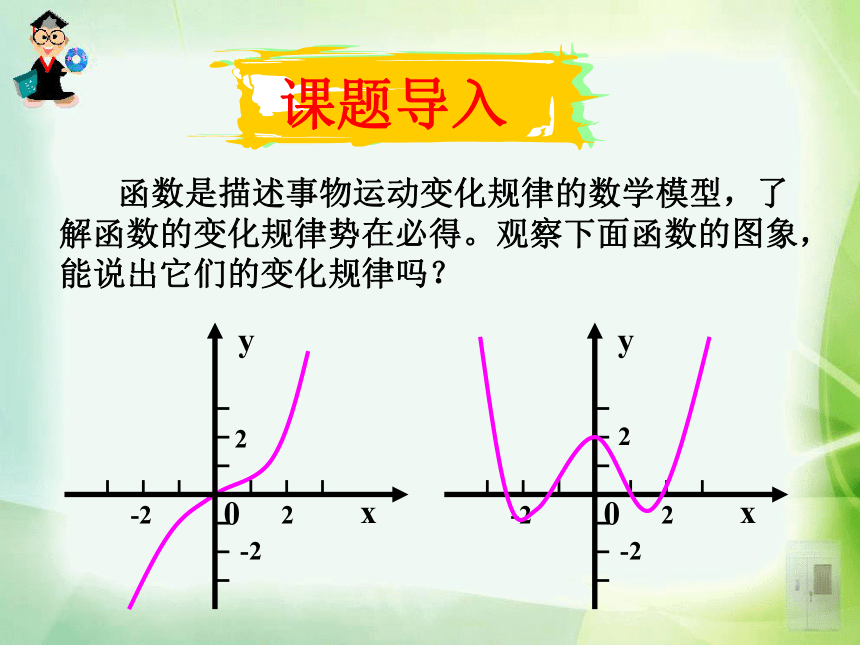
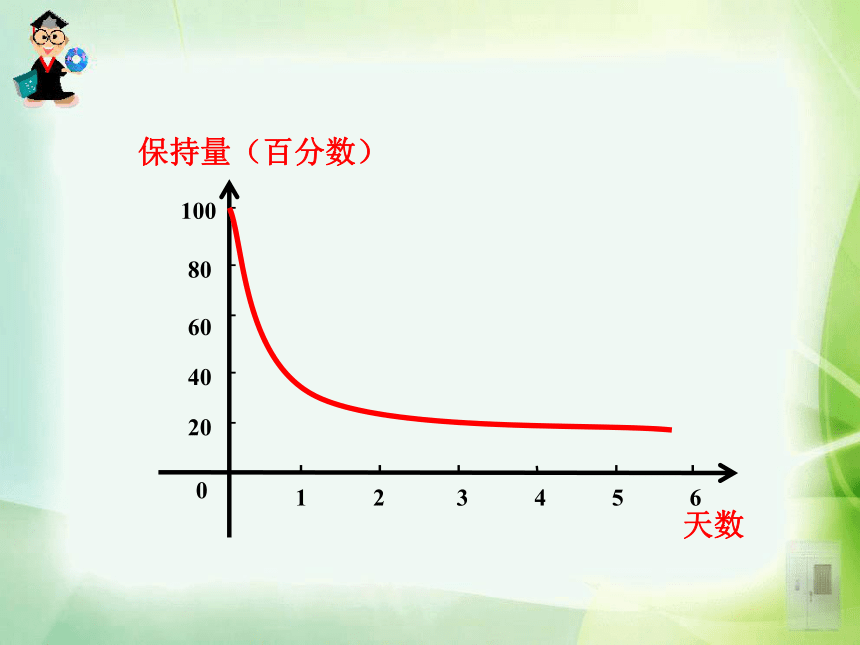
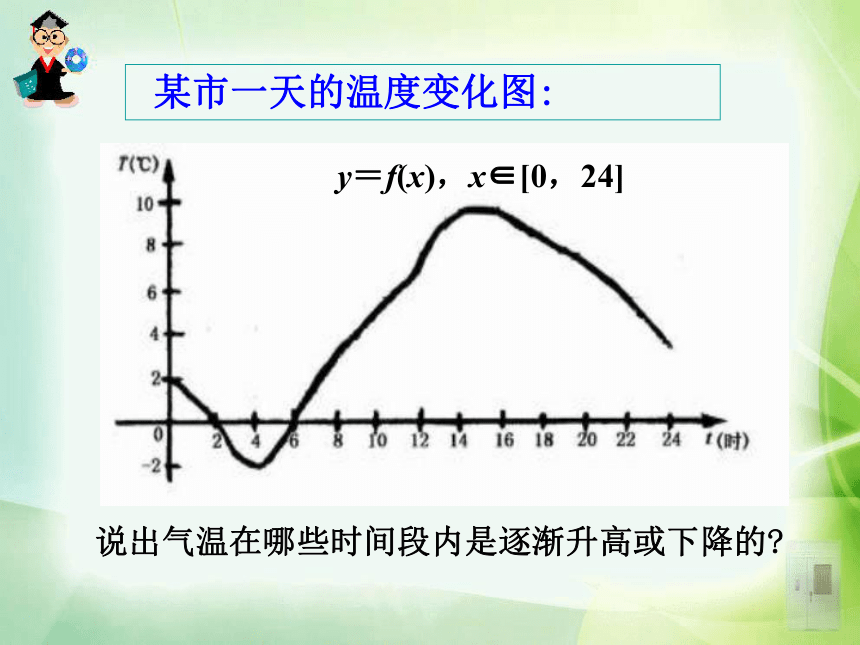
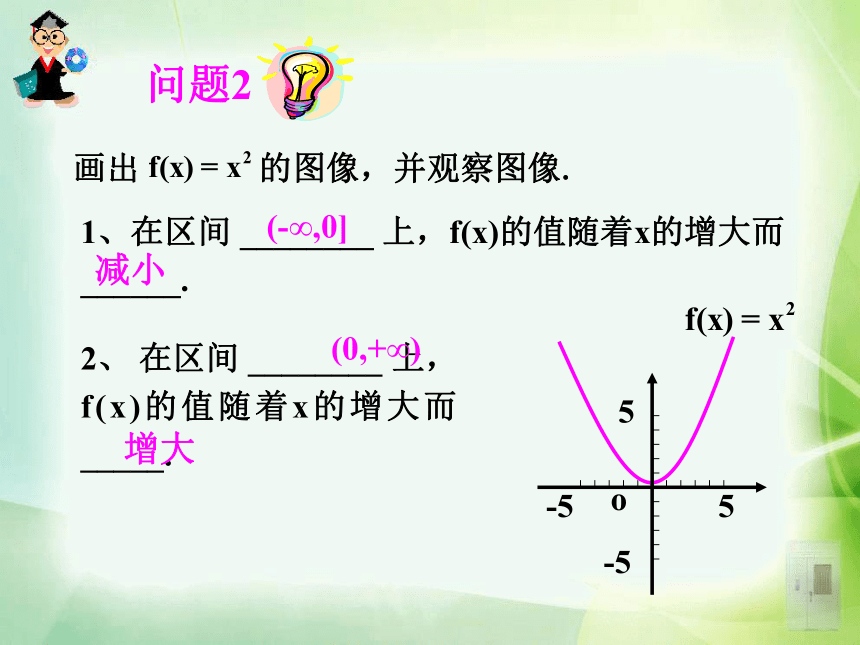
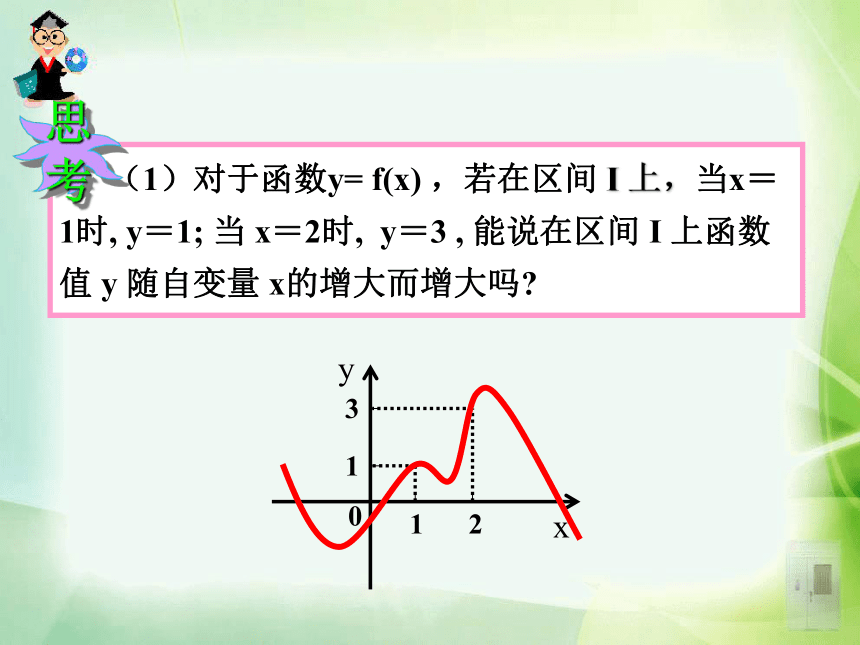
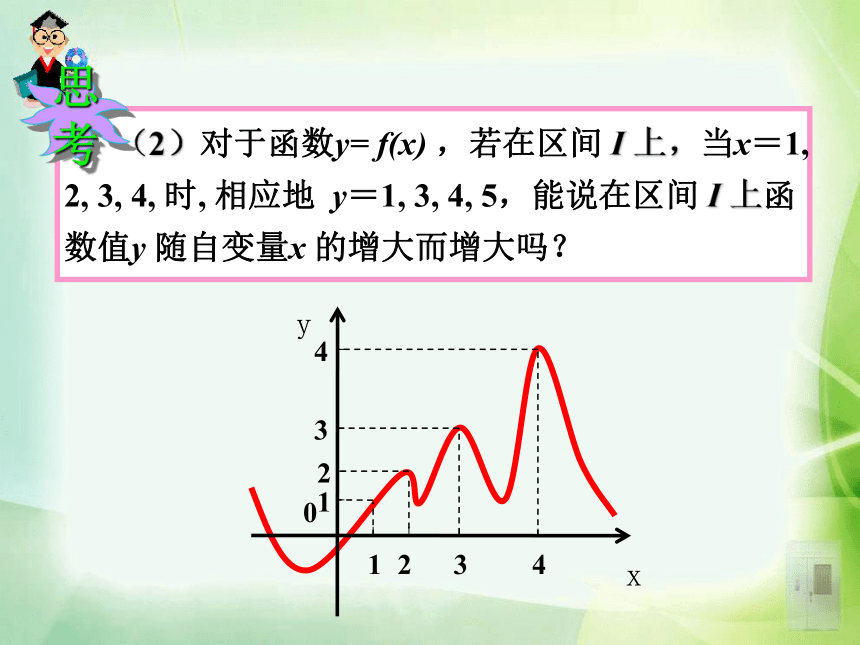
课件50张PPT。 函数是描述事物运动变化规律的数学模型，了解函数的变化规律势在必得。观察下面函数的图象，能说出它们的变化规律吗？ 某市一天的温度变化图:说出气温在哪些时间段内是逐渐升高或下降的?1.3.1 单调性与最大（小）值 理解函数的最大（小）值及其几何意义，学会运用函数图象理解和研究函数的性质． 通过实例，使学生体会到函数的最大（小）值，实际上是函数图象的最高（低）点的纵坐标，因而借助函数图象的直观性可得出函数的最值，有利于培养以形识数的解题意识． 利用函数的单调性和图象求函数的最大（小）值，解决日常生活中的实际问题，激发学生学习的积极性．函数的最大（小）值及其几何意义.利用函数的单调性求函数的最大（小）值.画出f(x)=x的图像，并观察其图像。2、在区间 ________上，随着x的增大，f(x)的值随着 ______. 1、从左至右图象上升还是下降 ____?上升增大1、在区间 ________ 上，f(x)的值随着x的增大而 ______.2、 在区间 ________ 上，f(x)的值随着x的增大而 _____. (-∞,0](0,+∞)减小增大x应该取区间I内所有实数若x取无数个呢?函数单调性的概念： 一般地，设函数y=f(x)的定义域为I，如果对于定义域I内的某个区间D内的任意两个自变量x1，x2，当x1f(x2) ，那么就说f(x)在区间D上是减函数 ,如图2. 1、函数的单调性是在定义域内的某个区间上的性质，是函数的局部性质. 2 、必须是对于区间D内的任意两个自变量x1，x2；当x1f(x2) 分别是增函数和减函数.在某区间上， 如果函数y=f(x)在某个区间上是增函数或是减函数，那么就说函数y=f(x)在这一区间具有（严格的）单调性，区间D叫做y=f(x)的单调区间.函数的单调性定义例1 下图是定义在区间[-4,5]上的函数y=f (x)，根据图像说出函数的单调区间，以及在每一单调区间上，它是增函数还是减函数？解：函数y=f(x)的单调区间有[-4，-2)，[-2，-1)，[-1，1)，[1，3)，[3，5],其中y=f (x)在区间
[-4，-2)， [-1，1)， [3，5]上是增函数，在区间
[-2，-1)， [1，3)上是减函数.证明：根据单调性的定义，设V1，V2是定义域(0，+∞)上的任意两个实数，且V10, V2- V1 >0取值定号作差变形结论用定义证明函数单调性的步骤是：（1）取值（2）作差变形（3）定号（4）判断根据单调性的定义得结论思考自己动手做一下吧{x∣x≠0}分两个区间(0，+∞)， （- ∞ ，0）来考虑其单调性.（2）在区间（- ∞ ，0）上，同理可得到函数f(x)=1/x 在（- ∞ ，0）上是减函数。综上所述，函数f(x)=1/x 在定义域上是减函数.下列两个函数的图象： f(x)< M?(0)=12、存在0，使得?(0)=1.1是此函数的最大值知识要点M是函数y= f (x)的最大值（maximum value）：是函数f(x)在定义域中既有最大值又有最小值.探究:函数单调性与函数的最值的关系（1）若函数y=f (x)在区间[m，n] (m（2）利用图象求函数的最值;
（3）利用函数单调性求函数的最值 .1.填表函数单调区间k >0k <0k >0k <0增函数减函数减函数增函数单调性函数单调区间单调性增函数增函数减函数减函数最大0.50.2-2 1.在一定范围内，生产效率随着工人数的增加而提高，当工人数达到某个数量时，生产效率达到最大值，而超过这个数量时，生产效率又随着工人数的增加而降低.由此可见，并非是工人越多，生产效率即越高.
2.增区间为：[8,12],[13,18];减区间为[12,13],[18,20].