7.2.1+复数的加、减运算及其几何意义2022-2023学年高一数学同步精讲 课件(共24张PPT)
文档属性
| 名称 | 7.2.1+复数的加、减运算及其几何意义2022-2023学年高一数学同步精讲 课件(共24张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-06 11:52:39 | ||
图片预览







文档简介
(共24张PPT)
§7.2.1 复数的加、减运算及其几何意义
§7.2 复数的四则运算
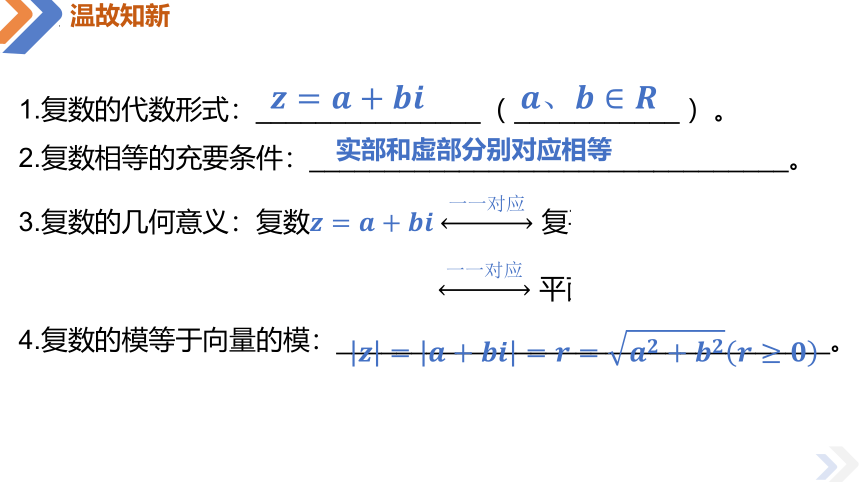
温故知新
1.复数的代数形式:_______________( ___________ )。
2.复数相等的充要条件:________________________________。
3.复数的几何意义:复数 复平面内的点
平面向量
4.复数的模等于向量的模:_________________________________。
实部和虚部分别对应相等
情景导入
在上一节,我们把实数集扩充到了复数集.引入新数集后,就要研究其中的数之间的运算.
下面就来讨论复数集中的运算问题:
复数如何进行四则运算呢?运算律仍成立吗?
复数的加法
复数的减法
典型例题精析
小结及随堂练习
复数的加法
01
探究新知
探究1:复数的加减法具体该如何运算?
引例:设,,则该如何表示?
在上述运算中,我们遵循了什么原则?
合并同类项
两个复数的加法运算可不可以类比上述原则进行呢?
设是任意两个复数,那么它们的和
复数的加法法则
学习新知
设是任意两个复数,那么它们的和
复数的加法法则
注意:
1.两个复数的和仍然是一个确定的复数;
2.当都是实数时,把它们看作复数时的和就是这两个实数的和;
3.两个复数相加,类似于两个多项式相加(合并同类项).
对于任意,有 ,
即,复数的加法满足交换律、结合律
复数加法运算律
探究新知
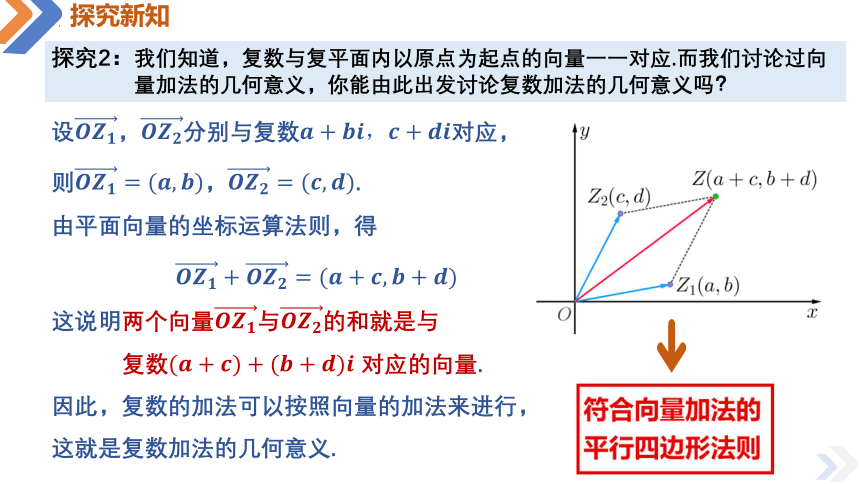
探究2:我们知道,复数与复平面内以原点为起点的向量一一对应.而我们讨论过向
量加法的几何意义,你能由此出发讨论复数加法的几何意义吗?
设,分别与复数对应,
则,.
由平面向量的坐标运算法则,得
这说明两个向量与的和就是与
复数 对应的向量.
因此,复数的加法可以按照向量的加法来进行,
这就是复数加法的几何意义.
复数的减法
02
再探新知
探究3:我们知道,实数的减法是加法的逆运算。
类比实数减法的意义,你认为该如何定义复数的减法?
我们规定,复数的减法是加法的逆运算,即把满足
的复数叫做复数减去复数的差,
记作.
根据复数相等的含义,
因此
所以
即
这就是复数的减法法则
1.两个复数的差仍然是一个确定的复数;
2.两个复数相减,类似于两个多项式相减(合并同类项)
再探新知
探究4:类比复数加法的几何意义,你能得出复数减法的几何意义吗?
设,分别与复数对应,
则,.
由平面向量的坐标运算法则,得
这说明两个向量与的差就是与
复数 对应的向量.
因此,复数的减法可以按照向量的减法来进行,
这就是复数减法的几何意义.
典型例题精析
03
典例精析
题型一:复数的加、减运算
例1.计算;
计算.
解: 原式
原式
例2.已知, ,为实数,
若,则
解:
,解得, ;
,
典例精析
题型一:复数的加、减运算
(1)复数的加、减运算类似于多项式的合并同类项:
①复数的实部与实部相加减,虚部与虚部相加减;
②把看作一个字母,类比多项式加减中的合并同类项;
(2)运算推广:对应复数的加法(或减法)可以推广到多个复数相加(或
相减)的混合运算,运算的结果仍然是一个复数
思维升华:复数代数形式的加、减法运算
【注:准确地提取复数的实部与虚部】
典例精析
题型二:复数加、减法的几何意义
例3.根据复数及其运算的几何意义,求复平面内的两点,
之间的距离.
解:因为复平面内的点对应的复数分别为,
,所以点,之间的距离为
分析:由于复平面内的点,,对应的复数分别为
由复数减法的几何意义知,复数对应
的向量为,从而点 之间的距离
典例精析
题型二:复数加、减法的几何意义
例4.如图所示,在□ 中,顶点分别为
求所表示的复数, 所表示的复数;
对角线所表示的复数;
对角线所表示的复数及的长度。
解:1)因为,所以所表示的复数为
因为, 所以所表示的复数为
2)因为
所以所表示的复数为
3)因为
所以所表示的复数为
所以
典例精析
题型二:复数加、减法的几何意义
(1)形转化为数:
利用几何意义可以把几何图形的变换转化成复数运算去处理.
(2)数转化为形:
对于一些复数运算也可以给予几何解释,使复数作为工具运用于几何之中.
思维升华:用复数加、减运算的几何意义解题的技巧
典例精析
题型三:复数加、减法及几何意义的应用
例4.设,,已知,,求.
解:法一:设,,
由题设知,,
又∵
∴
∵
∴
法二:作出,对应的向量,,使
∵,又,不共线(若,共线,
则或与题设矛盾), ∴平行四边形为菱形
又, ∴, 即四边形为正方形,
故.
典例精析
题型三:复数加、减法及几何意义的应用
(1)复数问题实数化:
设出复数 ,利用复数相等或模的概念,可把
条件转化为满足的关系式,利用方程思想求解.
(2)几何意义的应用:
在复平面内,对应的点为, 对应的点为 , 为坐
标原点,则四边形 OACB 满足:
①为平行四边形;
②若,则四边形为矩形;
③若,则四边形为菱形;
④若且则四边形 OACB 为正方形
思维升华:复数加、减法及几何意义的应用
小结及随堂练习
04
随堂练习
1.计算下列复数的和与差
①
②
2.计算:(1)
(2)
(3)
3.图中的向量对应的复数,
试做出下列运算结果对应的向量:
(1) (2) (3)
y
x
O
1
2
3
4
-1
-2
1
2
3
4
-1
-2
课时达标检测18(必做)
预习下一课(选做)
§7.2.1 复数的加、减运算及其几何意义
§7.2 复数的四则运算
温故知新
1.复数的代数形式:_______________( ___________ )。
2.复数相等的充要条件:________________________________。
3.复数的几何意义:复数 复平面内的点
平面向量
4.复数的模等于向量的模:_________________________________。
实部和虚部分别对应相等
情景导入
在上一节,我们把实数集扩充到了复数集.引入新数集后,就要研究其中的数之间的运算.
下面就来讨论复数集中的运算问题:
复数如何进行四则运算呢?运算律仍成立吗?
复数的加法
复数的减法
典型例题精析
小结及随堂练习
复数的加法
01
探究新知
探究1:复数的加减法具体该如何运算?
引例:设,,则该如何表示?
在上述运算中,我们遵循了什么原则?
合并同类项
两个复数的加法运算可不可以类比上述原则进行呢?
设是任意两个复数,那么它们的和
复数的加法法则
学习新知
设是任意两个复数,那么它们的和
复数的加法法则
注意:
1.两个复数的和仍然是一个确定的复数;
2.当都是实数时,把它们看作复数时的和就是这两个实数的和;
3.两个复数相加,类似于两个多项式相加(合并同类项).
对于任意,有 ,
即,复数的加法满足交换律、结合律
复数加法运算律
探究新知
探究2:我们知道,复数与复平面内以原点为起点的向量一一对应.而我们讨论过向
量加法的几何意义,你能由此出发讨论复数加法的几何意义吗?
设,分别与复数对应,
则,.
由平面向量的坐标运算法则,得
这说明两个向量与的和就是与
复数 对应的向量.
因此,复数的加法可以按照向量的加法来进行,
这就是复数加法的几何意义.
复数的减法
02
再探新知
探究3:我们知道,实数的减法是加法的逆运算。
类比实数减法的意义,你认为该如何定义复数的减法?
我们规定,复数的减法是加法的逆运算,即把满足
的复数叫做复数减去复数的差,
记作.
根据复数相等的含义,
因此
所以
即
这就是复数的减法法则
1.两个复数的差仍然是一个确定的复数;
2.两个复数相减,类似于两个多项式相减(合并同类项)
再探新知
探究4:类比复数加法的几何意义,你能得出复数减法的几何意义吗?
设,分别与复数对应,
则,.
由平面向量的坐标运算法则,得
这说明两个向量与的差就是与
复数 对应的向量.
因此,复数的减法可以按照向量的减法来进行,
这就是复数减法的几何意义.
典型例题精析
03
典例精析
题型一:复数的加、减运算
例1.计算;
计算.
解: 原式
原式
例2.已知, ,为实数,
若,则
解:
,解得, ;
,
典例精析
题型一:复数的加、减运算
(1)复数的加、减运算类似于多项式的合并同类项:
①复数的实部与实部相加减,虚部与虚部相加减;
②把看作一个字母,类比多项式加减中的合并同类项;
(2)运算推广:对应复数的加法(或减法)可以推广到多个复数相加(或
相减)的混合运算,运算的结果仍然是一个复数
思维升华:复数代数形式的加、减法运算
【注:准确地提取复数的实部与虚部】
典例精析
题型二:复数加、减法的几何意义
例3.根据复数及其运算的几何意义,求复平面内的两点,
之间的距离.
解:因为复平面内的点对应的复数分别为,
,所以点,之间的距离为
分析:由于复平面内的点,,对应的复数分别为
由复数减法的几何意义知,复数对应
的向量为,从而点 之间的距离
典例精析
题型二:复数加、减法的几何意义
例4.如图所示,在□ 中,顶点分别为
求所表示的复数, 所表示的复数;
对角线所表示的复数;
对角线所表示的复数及的长度。
解:1)因为,所以所表示的复数为
因为, 所以所表示的复数为
2)因为
所以所表示的复数为
3)因为
所以所表示的复数为
所以
典例精析
题型二:复数加、减法的几何意义
(1)形转化为数:
利用几何意义可以把几何图形的变换转化成复数运算去处理.
(2)数转化为形:
对于一些复数运算也可以给予几何解释,使复数作为工具运用于几何之中.
思维升华:用复数加、减运算的几何意义解题的技巧
典例精析
题型三:复数加、减法及几何意义的应用
例4.设,,已知,,求.
解:法一:设,,
由题设知,,
又∵
∴
∵
∴
法二:作出,对应的向量,,使
∵,又,不共线(若,共线,
则或与题设矛盾), ∴平行四边形为菱形
又, ∴, 即四边形为正方形,
故.
典例精析
题型三:复数加、减法及几何意义的应用
(1)复数问题实数化:
设出复数 ,利用复数相等或模的概念,可把
条件转化为满足的关系式,利用方程思想求解.
(2)几何意义的应用:
在复平面内,对应的点为, 对应的点为 , 为坐
标原点,则四边形 OACB 满足:
①为平行四边形;
②若,则四边形为矩形;
③若,则四边形为菱形;
④若且则四边形 OACB 为正方形
思维升华:复数加、减法及几何意义的应用
小结及随堂练习
04
随堂练习
1.计算下列复数的和与差
①
②
2.计算:(1)
(2)
(3)
3.图中的向量对应的复数,
试做出下列运算结果对应的向量:
(1) (2) (3)
y
x
O
1
2
3
4
-1
-2
1
2
3
4
-1
-2
课时达标检测18(必做)
预习下一课(选做)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
