【中学教材全解】2013-2014学年八年级数学(下)(上海科技版)第18章 勾股定理 检测题(含答案解析)
文档属性
| 名称 | 【中学教材全解】2013-2014学年八年级数学(下)(上海科技版)第18章 勾股定理 检测题(含答案解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 207.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-13 00:00:00 | ||
图片预览


文档简介
第18章 勾股定理检测题
(时间:90分钟,满分:100分)
一、选择题(每小题3分,共30分)
1.在△中,,,,则该三角形为( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰直角三角形
2.如果把直角三角形的两条直角边长同时扩大为原来的2倍,那么斜边长扩大为原来
的( )
A.1倍 B.2倍 C.3倍 D.4倍
3.下列说法中正确的是( )
A.已知 HYPERLINK "http://www.21cnjy.com" 是三角形的三边,则 HYPERLINK "http://www.21cnjy.com"
B.在直角三角形中,两边的平方和等于第三边的平方
C.在Rt△中,∠°,所以 HYPERLINK "http://www.21cnjy.com"
D.在Rt△中,∠°,所以 HYPERLINK "http://www.21cnjy.com"
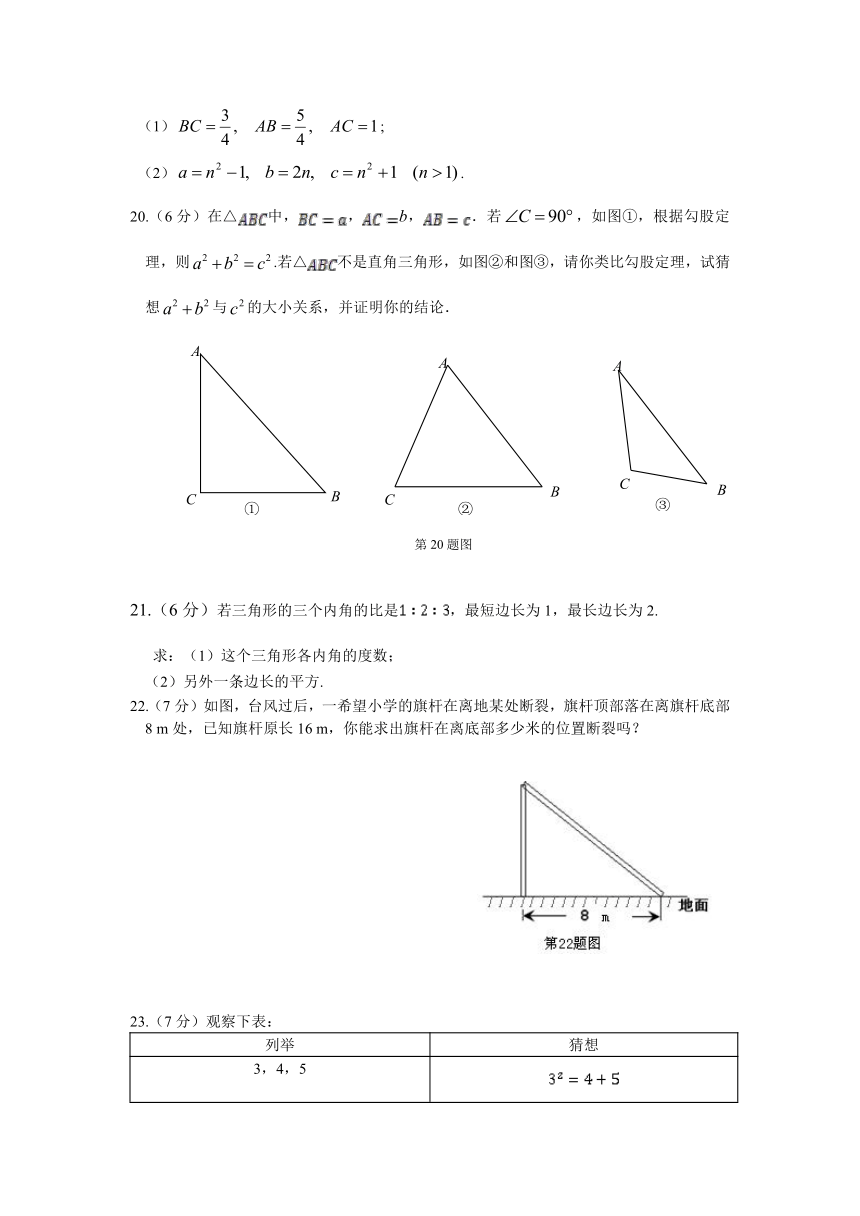
4.如图,已知正方形的面积为144,正方形的面积为169时,那么正方形的面积为( )
A.313 B.144 C.169 D.25
5.如图,在Rt△中,∠°, cm, cm,则其斜边上的高为( )
A.6 cm B.8.5 cm C. HYPERLINK "http://www.21cnjy.com" cm D. HYPERLINK "http://www.21cnjy.com" cm
6.下列满足条件的三角形中,不是直角三角形的是( )
A.三内角之比为 B.三边长的平方之比为
C.三边长之比为 D.三内角之比为
7.如图,在△中,∠°,,,点在上,且,,则的长为( )
A.6 B.7 C.8 D.9
( http: / / www.21cnjy.com )
8.如图,一圆柱高8 cm,底面半径为 HYPERLINK "http://www.21cnjy.com" cm,一只蚂蚁从点爬到点处吃食物,要爬行的最短路程是( )
A.6 cm B.8 cm C.10 cm D.12 cm
9.如果一个三角形的三边长满足,则这个三角形一定是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
10.在△中,三边长满足 HYPERLINK "http://www.21cnjy.com" ,则互余的一对角是( )
A.∠与∠ B.∠与∠ C.∠与∠ D.∠、∠、∠
二、填空题(每小题3分,共24分)
11.已知两条线段的长分别为5 cm、12 cm,当第三条线段长为________时,这三条线段可以构成一个直角三角形.
12.在△中, cm, cm,⊥于点,则_______.
13.在△中,若三边长分别为9、12、15,则两个这样的三角形拼成的长方形的面积为__________.
14. 如图,在Rt△中,,平分,交于点,且,,则点到的距离是________.
15.有一组勾股数,知道其中的两个数分别是17和8,则第三个数是 .
16. 若一个直角三角形的一条直角边长是,另一条直角边长比斜边长短,则该直角三角形的斜边长为 ________.
17.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7 cm,则正方形的面积之和为___________cm2.
18.如图,学校有一块长方形花圃,有极少 ( http: / / www.21cnjy.com )数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,他们仅仅少走了________步路(假设2步为1 m),却踩伤了花草.
三、解答题(共46分)
19.(6分)若△三边长满足下列条件,判断△是不是直角三角形,若是,请说明哪个角是直角.
(1) HYPERLINK "http://www.21cnjy.com" ;
(2) HYPERLINK "http://www.21cnjy.com" .
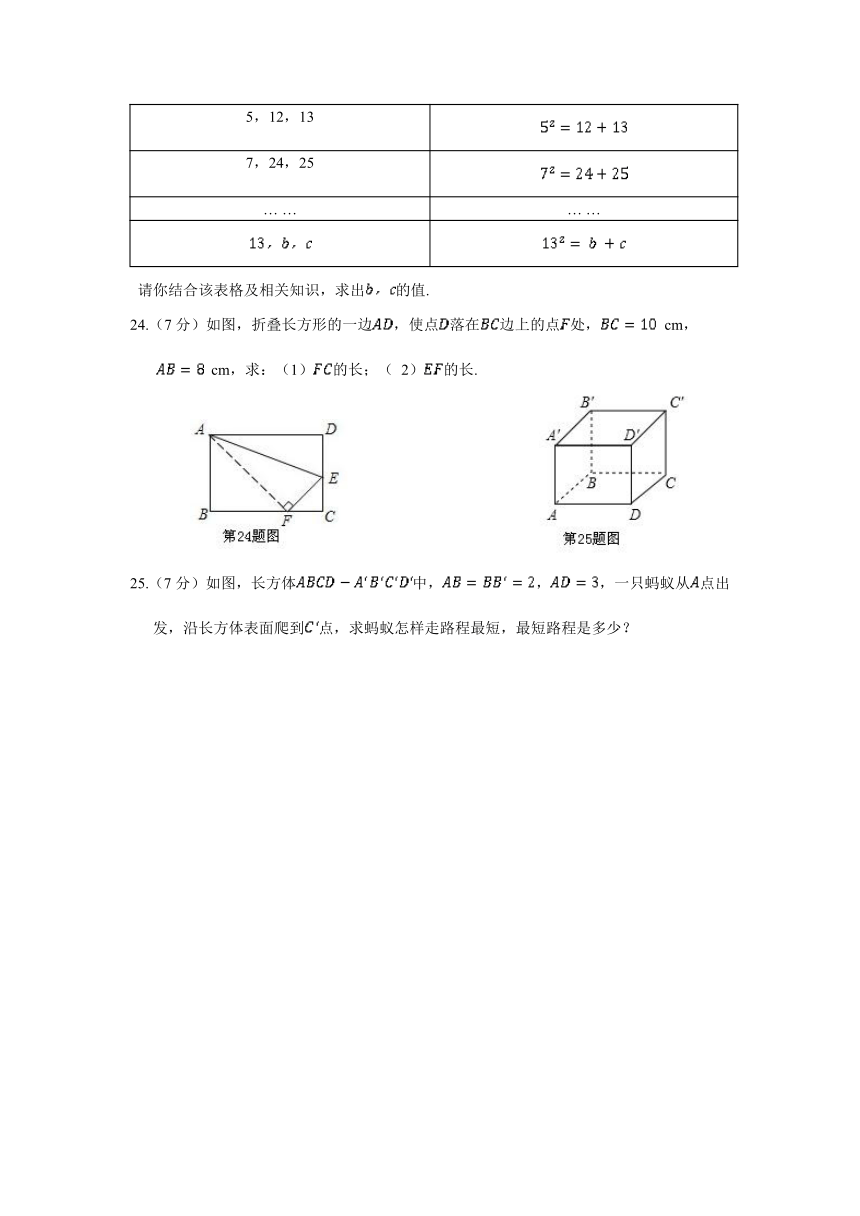
20.(6分)在△中,, HYPERLINK "http://www.21cnjy.com" ,.若 HYPERLINK "http://www.21cnjy.com" ,如图①,根据勾股定理,则 HYPERLINK "http://www.21cnjy.com" .若△不是直角三角形,如图②和图③,请你类比勾股定理,试猜想 HYPERLINK "http://www.21cnjy.com" 与 HYPERLINK "http://www.21cnjy.com" 的大小关系,并证明你的结论.
21.(6分)若三角形的三个内角的比是,最短边长为1,最长边长为2.
求:(1)这个三角形各内角的度数;
(2)另外一条边长的平方.
22.(7分)如图,台风过后,一希望小学的旗杆在离地某处断裂,旗杆顶部落在离旗杆底部8 m处,已知旗杆原长16 m,你能求出旗杆在离底部多少米的位置断裂吗?
23.(7分)观察下表:
列举 猜想
3,4,5 ( http: / / www.21cnjy.com )
5,12,13 ( http: / / www.21cnjy.com )
7,24,25 ( http: / / www.21cnjy.com )
… … … …
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
请你结合该表格及相关知识,求出的值.
24.(7分)如图,折叠长方形的一边,使点落在边上的点处, cm,
cm,求:(1)的长;( 2)的长.
25.(7分)如图,长方体中,,,一只蚂蚁从点出发,沿长方体表面爬到点,求蚂蚁怎样走路程最短,最短路程是多少?
第18章 勾股定理检测题参考答案
1. B 解析:在△中,由,,,可推出.由勾股定理的逆定理知此三角形是直角三角形,故选B.
2.B 解析:设原直角三角形的三边长分别是,且,则扩大后的三角形的斜边长为,即斜边长扩大为原来的2倍,故选B.
3.C 解析:A.不确定三角形是不是直角三角形,故A选项错误;B.不确定第三边是否为斜边,故B选项错误;C.∠C=90°,所以其对边为斜边,故C选项正确;D.∠B=90°,所以,故D选项错误.
4.D 解析:设三个正方形的边长依次为,由于三个正方形的三边组成一个直角三角形,所以,故,即.
5.C 解析:由勾股定理可知 cm,再由三角形的面积公式,有
HYPERLINK "http://www.21cnjy.com" ,得 HYPERLINK "http://www.21cnjy.com" .
6. D 解析:在A选项中,求出三角形的三个内角分别是30°,60°,90°;在B,C选项中,都符合勾股定理的条件,所以A,B,C选项中都是直角三角形.在D选项中,求出三角形的三个角分别是所以不是直角三角形,故选D.
7.C 解析:因为Rt△中,,所以由勾股定理得.因为,,所以.
8.C 解析:如图为圆柱的侧面展开图,∵ 为的中点,则就是蚂蚁爬行的最短路径.∵ ,
∴ .
∵ ,∴ ,即蚂蚁要爬行的最短路程是10 cm.
9.B 解析:由,整理,得,即,所以,符合,所以这个三角形一定是直角三角形.
10.B 解析:由,得,所以△是直角三角形,且是斜边,所以∠B=90°,从而互余的一对角是∠ ( http: / / www.21cnjy.com )与∠.
11. cm或13 cm 解析:根据勾股定理,知当12为直角边长时,第三条线段长为;当12为斜边长时,第三条线段长为.
12.15 cm 解析:如图,∵ 等腰三角形底边上的高、中线以及顶角的平分线三线合一,
∴ .∵,∴ .
∵ ,
∴ (cm).
13.108 解析:因为,所以△是直角三角形,且两条直角边长分别为9、12,则以两个这样的三角形拼成的长方形的面积为.
14. 3 解析:如图,过点作于.
因为,,,所以.
因为平分,,所以点到的距离.
15.15 解析:设第三个数是,①若为最长边,则,不是整数,不符合题意;② 若17为最长边,则,三边是整数,能构成勾股数,符合题意,故答案为: 15.
16. 解析:设直角三角形的斜边长是 ,则另一条直角边长是.根据勾股定理,得,解得,则斜边长是.
17.49 解析:正方形A,B,C,D的面积之和是最大的正方形的面积,即49 .
18.4 解析:在Rt△ABC中,,则,少走了(步).
19.解:(1)因为 ,
根据三边长满足的条件,可以判断△是直角三角形,其中∠为直角.
(2)因为,所以
,
根据三边长满足的条件,可以判断△是直角三角形,其中∠为直角.
20.解:如图①,若△是锐角三角形,则有 HYPERLINK "http://www.21cnjy.com" .证明如下:
过点作,垂足为,设为 HYPERLINK "http://www.21cnjy.com" ,则有 HYPERLINK "http://www.21cnjy.com" .在Rt△ACD中,
根据勾股定理,得AC2 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 CD2=AD2,即b2 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 x2= AD2. 在Rt△ABD中,根据勾股定理,得AD2=AB2 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 BD2,即AD2= c2 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 (a HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 x)2,即 HYPERLINK "http://www.21cnjy.com" ,∴ HYPERLINK "http://www.21cnjy.com" .
∵ HYPERLINK "http://www.21cnjy.com" ,∴ HYPERLINK "http://www.21cnjy.com" ,∴ HYPERLINK "http://www.21cnjy.com" .
如图②,若△是钝角三角形, HYPERLINK "http://www.21cnjy.com" 为钝角,则有 HYPERLINK "http://www.21cnjy.com" . 证明如下:
过点作,交的延长线于点.
设为 HYPERLINK "http://www.21cnjy.com" ,在Rt△BCD中,根据勾股定理,得 HYPERLINK "http://www.21cnjy.com" ,在Rt△ABD中,根据勾股定理,得AD2+ BD2= AB2,即 HYPERLINK "http://www.21cnjy.com" .
即 HYPERLINK "http://www.21cnjy.com" .
∵ HYPERLINK "http://www.21cnjy.com" ,∴ HYPERLINK "http://www.21cnjy.com" ,∴ HYPERLINK "http://www.21cnjy.com" .
21.解:(1)因为三个内角的比是,
所以设三个内角的度数分别为.
由,得,
所以三个内角的度数分别为.
(2)由(1)可知此三角形为直角三角形,则一条直角边长为1,斜边长为2.
设另外一条直角边长为,则,即.
所以另外一条边长的平方为3.
22.分析:旗杆折断的部分,未折断的部分和旗杆顶部离旗杆底部的部分构成了直角三角形,运用勾股定理可将折断的位置求出.
解:设旗杆未折断部分的长为 m,则折断部分的长为m,
根据勾股定理,得,
解得: m,即旗杆在离底部6 m处断裂.
23.分析:根据已知条件可找出规律;根据此规律可求出的值.
解:由3,4,5: ;
5,12,13: ;
7,24,25: .
故,,
解得,,即.
24.分析:(1)由于△翻折得到△,所以,则在Rt△中,可求得 的长,从而的长可求;
(2)由于,可设的长为,在Rt△中,利用勾股定理求解即可.
解:(1)由题意,得(cm),
在Rt△中,∵ ,∴ (cm),
∴ (cm).
(2)由题意,得,设的长为y,则EC=8-y.
在Rt△ ( http: / / www.21cnjy.com )中,由勾股定理,得,
解得y=5,即的长为5 cm.
25.分析:要求蚂蚁爬行的最短路程,需将长方体的侧面展开,进而根据“两点之间线段最短”得出结果.
解:如图(1),把长方体剪开,则成长方形,宽为,长为,
连接,则 ( http: / / www.21cnjy.com )为直角三角形,由勾股定理,得
.
如图(2),把长方体剪开,则成长方形,宽为,长为,
连接,则 ( http: / / www.21cnjy.com )为直角三角形,同理,由勾股定理,得.
∴ 蚂蚁从点出发穿过到达点路程最短,最短路程是5.
A
B
C
第4题图
第7题图
A
B
C
D
第14题图
A
B
C
A
B
C
A
B
C
①
② = 1 \* GB3 ①
③ = 1 \* GB3 ①
第20题图
A
B
C
D
第14题答图
E
(时间:90分钟,满分:100分)
一、选择题(每小题3分,共30分)
1.在△中,,,,则该三角形为( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰直角三角形
2.如果把直角三角形的两条直角边长同时扩大为原来的2倍,那么斜边长扩大为原来
的( )
A.1倍 B.2倍 C.3倍 D.4倍
3.下列说法中正确的是( )
A.已知 HYPERLINK "http://www.21cnjy.com" 是三角形的三边,则 HYPERLINK "http://www.21cnjy.com"
B.在直角三角形中,两边的平方和等于第三边的平方
C.在Rt△中,∠°,所以 HYPERLINK "http://www.21cnjy.com"
D.在Rt△中,∠°,所以 HYPERLINK "http://www.21cnjy.com"
4.如图,已知正方形的面积为144,正方形的面积为169时,那么正方形的面积为( )
A.313 B.144 C.169 D.25
5.如图,在Rt△中,∠°, cm, cm,则其斜边上的高为( )
A.6 cm B.8.5 cm C. HYPERLINK "http://www.21cnjy.com" cm D. HYPERLINK "http://www.21cnjy.com" cm
6.下列满足条件的三角形中,不是直角三角形的是( )
A.三内角之比为 B.三边长的平方之比为
C.三边长之比为 D.三内角之比为
7.如图,在△中,∠°,,,点在上,且,,则的长为( )
A.6 B.7 C.8 D.9
( http: / / www.21cnjy.com )
8.如图,一圆柱高8 cm,底面半径为 HYPERLINK "http://www.21cnjy.com" cm,一只蚂蚁从点爬到点处吃食物,要爬行的最短路程是( )
A.6 cm B.8 cm C.10 cm D.12 cm
9.如果一个三角形的三边长满足,则这个三角形一定是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.等腰三角形
10.在△中,三边长满足 HYPERLINK "http://www.21cnjy.com" ,则互余的一对角是( )
A.∠与∠ B.∠与∠ C.∠与∠ D.∠、∠、∠
二、填空题(每小题3分,共24分)
11.已知两条线段的长分别为5 cm、12 cm,当第三条线段长为________时,这三条线段可以构成一个直角三角形.
12.在△中, cm, cm,⊥于点,则_______.
13.在△中,若三边长分别为9、12、15,则两个这样的三角形拼成的长方形的面积为__________.
14. 如图,在Rt△中,,平分,交于点,且,,则点到的距离是________.
15.有一组勾股数,知道其中的两个数分别是17和8,则第三个数是 .
16. 若一个直角三角形的一条直角边长是,另一条直角边长比斜边长短,则该直角三角形的斜边长为 ________.
17.如图,所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大的正方形的边长为7 cm,则正方形的面积之和为___________cm2.
18.如图,学校有一块长方形花圃,有极少 ( http: / / www.21cnjy.com )数人为了避开拐角走“捷径”,在花圃内走出了一条“路”,他们仅仅少走了________步路(假设2步为1 m),却踩伤了花草.
三、解答题(共46分)
19.(6分)若△三边长满足下列条件,判断△是不是直角三角形,若是,请说明哪个角是直角.
(1) HYPERLINK "http://www.21cnjy.com" ;
(2) HYPERLINK "http://www.21cnjy.com" .
20.(6分)在△中,, HYPERLINK "http://www.21cnjy.com" ,.若 HYPERLINK "http://www.21cnjy.com" ,如图①,根据勾股定理,则 HYPERLINK "http://www.21cnjy.com" .若△不是直角三角形,如图②和图③,请你类比勾股定理,试猜想 HYPERLINK "http://www.21cnjy.com" 与 HYPERLINK "http://www.21cnjy.com" 的大小关系,并证明你的结论.
21.(6分)若三角形的三个内角的比是,最短边长为1,最长边长为2.
求:(1)这个三角形各内角的度数;
(2)另外一条边长的平方.
22.(7分)如图,台风过后,一希望小学的旗杆在离地某处断裂,旗杆顶部落在离旗杆底部8 m处,已知旗杆原长16 m,你能求出旗杆在离底部多少米的位置断裂吗?
23.(7分)观察下表:
列举 猜想
3,4,5 ( http: / / www.21cnjy.com )
5,12,13 ( http: / / www.21cnjy.com )
7,24,25 ( http: / / www.21cnjy.com )
… … … …
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
请你结合该表格及相关知识,求出的值.
24.(7分)如图,折叠长方形的一边,使点落在边上的点处, cm,
cm,求:(1)的长;( 2)的长.
25.(7分)如图,长方体中,,,一只蚂蚁从点出发,沿长方体表面爬到点,求蚂蚁怎样走路程最短,最短路程是多少?
第18章 勾股定理检测题参考答案
1. B 解析:在△中,由,,,可推出.由勾股定理的逆定理知此三角形是直角三角形,故选B.
2.B 解析:设原直角三角形的三边长分别是,且,则扩大后的三角形的斜边长为,即斜边长扩大为原来的2倍,故选B.
3.C 解析:A.不确定三角形是不是直角三角形,故A选项错误;B.不确定第三边是否为斜边,故B选项错误;C.∠C=90°,所以其对边为斜边,故C选项正确;D.∠B=90°,所以,故D选项错误.
4.D 解析:设三个正方形的边长依次为,由于三个正方形的三边组成一个直角三角形,所以,故,即.
5.C 解析:由勾股定理可知 cm,再由三角形的面积公式,有
HYPERLINK "http://www.21cnjy.com" ,得 HYPERLINK "http://www.21cnjy.com" .
6. D 解析:在A选项中,求出三角形的三个内角分别是30°,60°,90°;在B,C选项中,都符合勾股定理的条件,所以A,B,C选项中都是直角三角形.在D选项中,求出三角形的三个角分别是所以不是直角三角形,故选D.
7.C 解析:因为Rt△中,,所以由勾股定理得.因为,,所以.
8.C 解析:如图为圆柱的侧面展开图,∵ 为的中点,则就是蚂蚁爬行的最短路径.∵ ,
∴ .
∵ ,∴ ,即蚂蚁要爬行的最短路程是10 cm.
9.B 解析:由,整理,得,即,所以,符合,所以这个三角形一定是直角三角形.
10.B 解析:由,得,所以△是直角三角形,且是斜边,所以∠B=90°,从而互余的一对角是∠ ( http: / / www.21cnjy.com )与∠.
11. cm或13 cm 解析:根据勾股定理,知当12为直角边长时,第三条线段长为;当12为斜边长时,第三条线段长为.
12.15 cm 解析:如图,∵ 等腰三角形底边上的高、中线以及顶角的平分线三线合一,
∴ .∵,∴ .
∵ ,
∴ (cm).
13.108 解析:因为,所以△是直角三角形,且两条直角边长分别为9、12,则以两个这样的三角形拼成的长方形的面积为.
14. 3 解析:如图,过点作于.
因为,,,所以.
因为平分,,所以点到的距离.
15.15 解析:设第三个数是,①若为最长边,则,不是整数,不符合题意;② 若17为最长边,则,三边是整数,能构成勾股数,符合题意,故答案为: 15.
16. 解析:设直角三角形的斜边长是 ,则另一条直角边长是.根据勾股定理,得,解得,则斜边长是.
17.49 解析:正方形A,B,C,D的面积之和是最大的正方形的面积,即49 .
18.4 解析:在Rt△ABC中,,则,少走了(步).
19.解:(1)因为 ,
根据三边长满足的条件,可以判断△是直角三角形,其中∠为直角.
(2)因为,所以
,
根据三边长满足的条件,可以判断△是直角三角形,其中∠为直角.
20.解:如图①,若△是锐角三角形,则有 HYPERLINK "http://www.21cnjy.com" .证明如下:
过点作,垂足为,设为 HYPERLINK "http://www.21cnjy.com" ,则有 HYPERLINK "http://www.21cnjy.com" .在Rt△ACD中,
根据勾股定理,得AC2 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 CD2=AD2,即b2 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 x2= AD2. 在Rt△ABD中,根据勾股定理,得AD2=AB2 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 BD2,即AD2= c2 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 (a HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 x)2,即 HYPERLINK "http://www.21cnjy.com" ,∴ HYPERLINK "http://www.21cnjy.com" .
∵ HYPERLINK "http://www.21cnjy.com" ,∴ HYPERLINK "http://www.21cnjy.com" ,∴ HYPERLINK "http://www.21cnjy.com" .
如图②,若△是钝角三角形, HYPERLINK "http://www.21cnjy.com" 为钝角,则有 HYPERLINK "http://www.21cnjy.com" . 证明如下:
过点作,交的延长线于点.
设为 HYPERLINK "http://www.21cnjy.com" ,在Rt△BCD中,根据勾股定理,得 HYPERLINK "http://www.21cnjy.com" ,在Rt△ABD中,根据勾股定理,得AD2+ BD2= AB2,即 HYPERLINK "http://www.21cnjy.com" .
即 HYPERLINK "http://www.21cnjy.com" .
∵ HYPERLINK "http://www.21cnjy.com" ,∴ HYPERLINK "http://www.21cnjy.com" ,∴ HYPERLINK "http://www.21cnjy.com" .
21.解:(1)因为三个内角的比是,
所以设三个内角的度数分别为.
由,得,
所以三个内角的度数分别为.
(2)由(1)可知此三角形为直角三角形,则一条直角边长为1,斜边长为2.
设另外一条直角边长为,则,即.
所以另外一条边长的平方为3.
22.分析:旗杆折断的部分,未折断的部分和旗杆顶部离旗杆底部的部分构成了直角三角形,运用勾股定理可将折断的位置求出.
解:设旗杆未折断部分的长为 m,则折断部分的长为m,
根据勾股定理,得,
解得: m,即旗杆在离底部6 m处断裂.
23.分析:根据已知条件可找出规律;根据此规律可求出的值.
解:由3,4,5: ;
5,12,13: ;
7,24,25: .
故,,
解得,,即.
24.分析:(1)由于△翻折得到△,所以,则在Rt△中,可求得 的长,从而的长可求;
(2)由于,可设的长为,在Rt△中,利用勾股定理求解即可.
解:(1)由题意,得(cm),
在Rt△中,∵ ,∴ (cm),
∴ (cm).
(2)由题意,得,设的长为y,则EC=8-y.
在Rt△ ( http: / / www.21cnjy.com )中,由勾股定理,得,
解得y=5,即的长为5 cm.
25.分析:要求蚂蚁爬行的最短路程,需将长方体的侧面展开,进而根据“两点之间线段最短”得出结果.
解:如图(1),把长方体剪开,则成长方形,宽为,长为,
连接,则 ( http: / / www.21cnjy.com )为直角三角形,由勾股定理,得
.
如图(2),把长方体剪开,则成长方形,宽为,长为,
连接,则 ( http: / / www.21cnjy.com )为直角三角形,同理,由勾股定理,得.
∴ 蚂蚁从点出发穿过到达点路程最短,最短路程是5.
A
B
C
第4题图
第7题图
A
B
C
D
第14题图
A
B
C
A
B
C
A
B
C
①
② = 1 \* GB3 ①
③ = 1 \* GB3 ①
第20题图
A
B
C
D
第14题答图
E
