第十八章 平行四边形 单元检测(无答案) 2022-2023学年人教版八年级数学下册
文档属性
| 名称 | 第十八章 平行四边形 单元检测(无答案) 2022-2023学年人教版八年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 252.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-07 00:00:00 | ||
图片预览


文档简介
第十八章 平行四边形
班级______ 姓名_______ 学号_____
一、选择题
1.平行四边形的周长为24cm,相邻两边的差为2cm,则平行四边形的各边长为( )
A.4cm,4cm,8cm,8cm
B.5cm,5cm,7cm,7cm
C.5.5cm,5.5cm,6.5cm,6.5cm
D.3cm,3cm,9cm,9cm
2. 如图,要测定被池塘隔开的 , 两点的距离,可以在 外选一点 ,连接 ,,并分别找出它们的中点 ,,连接 .现测得 ,,,则 ( )
A. B. C. D.
3. 如图,在平行四边形 中, 的平分线 交 于点 ,,,则平行四边形 的周长为 ( )
A. B. C. D.
4. 已知菱形的边长为 ,一个内角为 ,则该菱形较长的对角线的长是 ( )
A. B. C. D.
5.如图,在平面直角坐标系中, ABCD的顶点A(﹣1,﹣2)、D(1,1)、C(5,2),则顶点B的坐标为( )
A.(﹣1,3) B.(4,﹣1) C.(3,﹣1) D.(﹣1,4)
6.如图,四边形ABCD为正方形,A点坐标为(﹣1,0),点B,C,D分别在坐标轴上,则正方形的周长是( )
A.4 B.3 C.4 D.2
7. 如图,在四边形 中,,,,点 从 出发以 的速度向 运动,点 从 出发以 的速度向 运动,两点同时出发,当点 运动到点 时,点 也随之停止运动.当运动时间为 秒时,以 ,,,,, 任意四个点为顶点的四边形中同时存在两个平行四边形,则 的值是( )
A. B. C. D.
8. 如图,已知 中,,点 , 分别在 , 边上,且 等于 ,,点 ,, 分别是 ,, 的中点,则 的长为( )
A. B. C. D.
9. 如图,矩形 的对角线 , 相交于点 ,,,若 ,则四边形 的周长为 ( )
A. B. C. D.
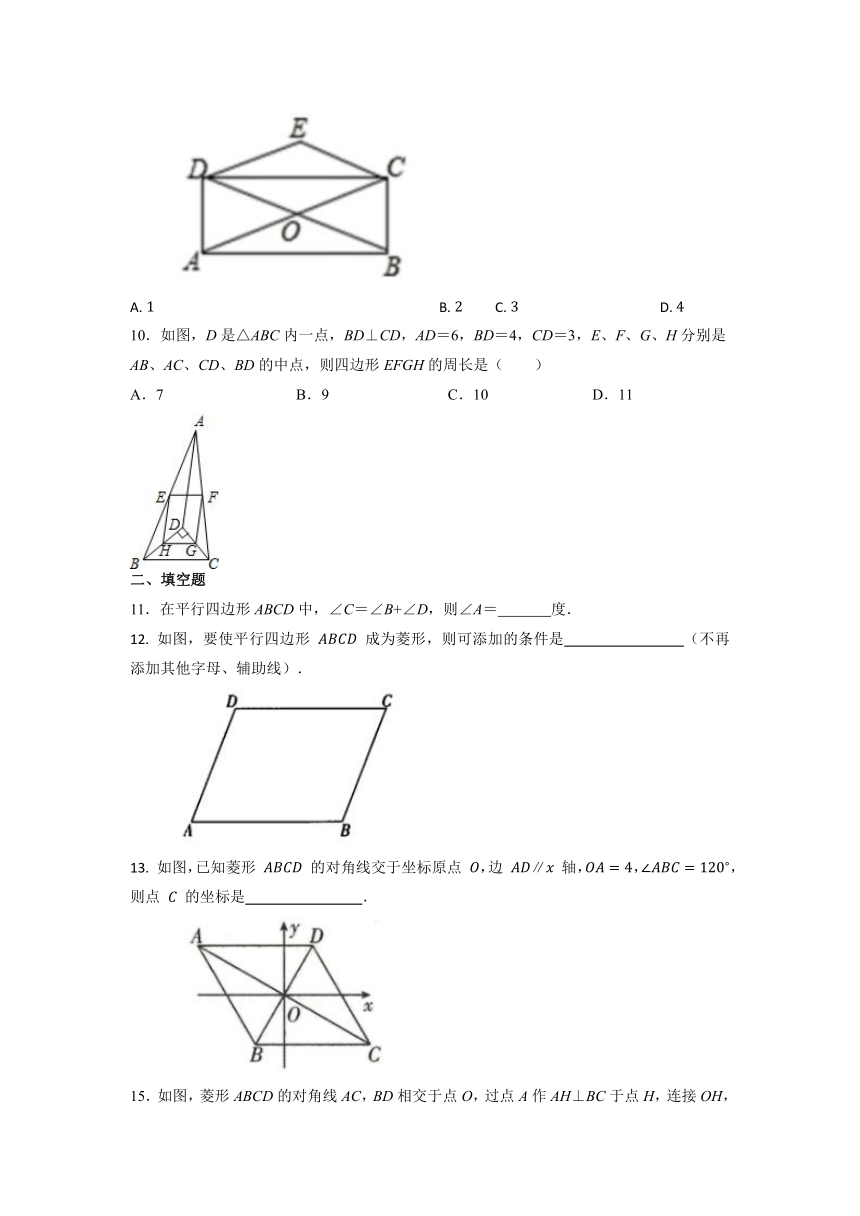
10.如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是( )
A.7 B.9 C.10 D.11
二、填空题
11.在平行四边形ABCD中,∠C=∠B+∠D,则∠A= 度.
12. 如图,要使平行四边形 成为菱形,则可添加的条件是 (不再添加其他字母、辅助线).
13. 如图,已知菱形 的对角线交于坐标原点 ,边 轴,,,则点 的坐标是 .
15.如图,菱形ABCD的对角线AC,BD相交于点O,过点A作AH⊥BC于点H,连接OH,若OB=4,S菱形ABCD=24,则OH的长为 .
16.如图所示,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=4,BC=10,则EF的长为 .
17. 如图,菱形 和菱形 的边长分别为 和 ,,则阴影部分面积是 .(结果保留根号)
18. 如图,在平行四边形 中,,,,动点 从 出发,以 个单位每秒的速度从 向 运动,同时动点 以相同速度从点 出发,沿 方向在 的延长线上运动,设运动时间为 ,连接 ,.探究:①当 时,四边形 是菱形;②当 时,四边形 是矩形.
三、解答题
19. 如图,点 是正方形 内一点, 是等边三角形,连接 ,,延长 交 于点 .
(1)求证:;
(2)求 的度数.
20.(6分)如图,E、F分别是矩形ABCD的边AD、AB上的点,EF=EC,且EF⊥EC.求证:BE平分∠ABC.
21.如图,在 ABCD中,点E、F分别在边BC和AD上,且BE=DF.
(1)求证:△ABE≌△CDF.
(2)求证:四边形AECF是平行四边形.
22. 如图,四边形 为菱形, 在 的延长线上, 在 的反向延长线上,且 .
求证:.
23. 如图①,在矩形纸片 中,,,折叠纸片使 点落在边 上的 处,折痕为 ,过点 作 交 于点 ,连接 .
(1)求证:四边形 为菱形;
(2)当点 在 边上移动时,折痕的端点 , 也随之移动.
①当点 与点 重合时(如图②),求菱形 的边长;
②若限定 , 分别在边 , 上移动,求出点 在边 上移动的最大距离.
24.如图,ABCD是矩形,AC=CF,E为AF的中点.求证:DE⊥BE.
25.如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°
(1)求证:四边形ABCD是矩形;
(2)若DE⊥AC交BC于E,∠ADB:∠CDB=2:3,则∠BDE的度数是多少?
班级______ 姓名_______ 学号_____
一、选择题
1.平行四边形的周长为24cm,相邻两边的差为2cm,则平行四边形的各边长为( )
A.4cm,4cm,8cm,8cm
B.5cm,5cm,7cm,7cm
C.5.5cm,5.5cm,6.5cm,6.5cm
D.3cm,3cm,9cm,9cm
2. 如图,要测定被池塘隔开的 , 两点的距离,可以在 外选一点 ,连接 ,,并分别找出它们的中点 ,,连接 .现测得 ,,,则 ( )
A. B. C. D.
3. 如图,在平行四边形 中, 的平分线 交 于点 ,,,则平行四边形 的周长为 ( )
A. B. C. D.
4. 已知菱形的边长为 ,一个内角为 ,则该菱形较长的对角线的长是 ( )
A. B. C. D.
5.如图,在平面直角坐标系中, ABCD的顶点A(﹣1,﹣2)、D(1,1)、C(5,2),则顶点B的坐标为( )
A.(﹣1,3) B.(4,﹣1) C.(3,﹣1) D.(﹣1,4)
6.如图,四边形ABCD为正方形,A点坐标为(﹣1,0),点B,C,D分别在坐标轴上,则正方形的周长是( )
A.4 B.3 C.4 D.2
7. 如图,在四边形 中,,,,点 从 出发以 的速度向 运动,点 从 出发以 的速度向 运动,两点同时出发,当点 运动到点 时,点 也随之停止运动.当运动时间为 秒时,以 ,,,,, 任意四个点为顶点的四边形中同时存在两个平行四边形,则 的值是( )
A. B. C. D.
8. 如图,已知 中,,点 , 分别在 , 边上,且 等于 ,,点 ,, 分别是 ,, 的中点,则 的长为( )
A. B. C. D.
9. 如图,矩形 的对角线 , 相交于点 ,,,若 ,则四边形 的周长为 ( )
A. B. C. D.
10.如图,D是△ABC内一点,BD⊥CD,AD=6,BD=4,CD=3,E、F、G、H分别是AB、AC、CD、BD的中点,则四边形EFGH的周长是( )
A.7 B.9 C.10 D.11
二、填空题
11.在平行四边形ABCD中,∠C=∠B+∠D,则∠A= 度.
12. 如图,要使平行四边形 成为菱形,则可添加的条件是 (不再添加其他字母、辅助线).
13. 如图,已知菱形 的对角线交于坐标原点 ,边 轴,,,则点 的坐标是 .
15.如图,菱形ABCD的对角线AC,BD相交于点O,过点A作AH⊥BC于点H,连接OH,若OB=4,S菱形ABCD=24,则OH的长为 .
16.如图所示,DE为△ABC的中位线,点F在DE上,且∠AFB=90°,若AB=4,BC=10,则EF的长为 .
17. 如图,菱形 和菱形 的边长分别为 和 ,,则阴影部分面积是 .(结果保留根号)
18. 如图,在平行四边形 中,,,,动点 从 出发,以 个单位每秒的速度从 向 运动,同时动点 以相同速度从点 出发,沿 方向在 的延长线上运动,设运动时间为 ,连接 ,.探究:①当 时,四边形 是菱形;②当 时,四边形 是矩形.
三、解答题
19. 如图,点 是正方形 内一点, 是等边三角形,连接 ,,延长 交 于点 .
(1)求证:;
(2)求 的度数.
20.(6分)如图,E、F分别是矩形ABCD的边AD、AB上的点,EF=EC,且EF⊥EC.求证:BE平分∠ABC.
21.如图,在 ABCD中,点E、F分别在边BC和AD上,且BE=DF.
(1)求证:△ABE≌△CDF.
(2)求证:四边形AECF是平行四边形.
22. 如图,四边形 为菱形, 在 的延长线上, 在 的反向延长线上,且 .
求证:.
23. 如图①,在矩形纸片 中,,,折叠纸片使 点落在边 上的 处,折痕为 ,过点 作 交 于点 ,连接 .
(1)求证:四边形 为菱形;
(2)当点 在 边上移动时,折痕的端点 , 也随之移动.
①当点 与点 重合时(如图②),求菱形 的边长;
②若限定 , 分别在边 , 上移动,求出点 在边 上移动的最大距离.
24.如图,ABCD是矩形,AC=CF,E为AF的中点.求证:DE⊥BE.
25.如图,四边形ABCD中,对角线AC、BD相交于点O,AO=CO,BO=DO,且∠ABC+∠ADC=180°
(1)求证:四边形ABCD是矩形;
(2)若DE⊥AC交BC于E,∠ADB:∠CDB=2:3,则∠BDE的度数是多少?
