青岛版九年级下册6.7 利用画树状图和列表计算概率 课件(共21张PPT)
文档属性
| 名称 | 青岛版九年级下册6.7 利用画树状图和列表计算概率 课件(共21张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 229.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-07 00:00:00 | ||
图片预览








文档简介
(共21张PPT)
6.1 随机事件
第 6 章 事件的概率
6.7 利用画树状图和列表计算概率
教学目标
1、知识与能力:使学生在具体情境中了解概率的意义,能够运用一些方法计算简单的事件发生的概率,并阐述理由。
2、过程与方法:经历试验、列表、统计、计算、设计等活动,学生在具体情景中分析事件,计算其发生的概率。
3、情感、态度与价值观:通过丰富的数学活动,交流成功的经验,体验数学活动充满着探索和创造,体会数学的应用价值,培养积极思维的学习习惯。
新课导入
甲乙两村之间有A、B两条道路,小亮从甲村去往乙村,大刚从乙村去往甲村,二人同时出发。如果每人从A、B两条道路中随机选择一条,而且他们都不知道对方的选择,那么二人图途中相遇的概率是多少?
分析:这个问题与我们之前学过的问题有些不同,不能直接列出所有等可能的情况,那有没有不重不漏的列出所有结果的方法呢?我们今天就来研究下此类问题。
探究新知
一、认识树状图法求概率
思考问题
(1)小亮有几条路可以选择?随机选择一条路的可能性是相同?
(2)大刚有几条路可供选择?每条道路选中的可能性是否相同?
分析:由于小亮走道路A或B有两种可能,可画出同一点出发的两个箭头分别表示小亮走A或走B。当小亮走道路A时,由于大刚走道路A或B也有两种可能,所以在表示小亮走A的箭头前面再画出两个箭头,分别表示当小亮走道路A时大刚可能走道路A或道路B。同样地,在表示小亮走B的箭头前面再画出两个箭头,分别表示当小亮走道路B时,大刚可能揍道路A或道路B。
所有等可能性结果共有____种,
这四种情况有没有重复?
还有没有其他的没有列出的结果?其中两人相遇的情况有______种.
P(相遇)=_________
这种图像一棵横倒的树,我们叫它树状图.
四
二
AB(不相遇)
大刚
小亮
AA(相遇)
BA(不相遇)
BB(相遇)
走A
走B
走A
走B
走A
走B
AB(不相遇)
大刚
小亮
AA(相遇)
BA(不相遇)
BB(相遇)
走A
走B
走A
走B
走A
走B
小亮和大刚地位相同,也可表示如下:
所有等可能的结果共有4种:AA,AB,BA,BB,其中两人相遇的情况有2种,
所以,P(相遇)=
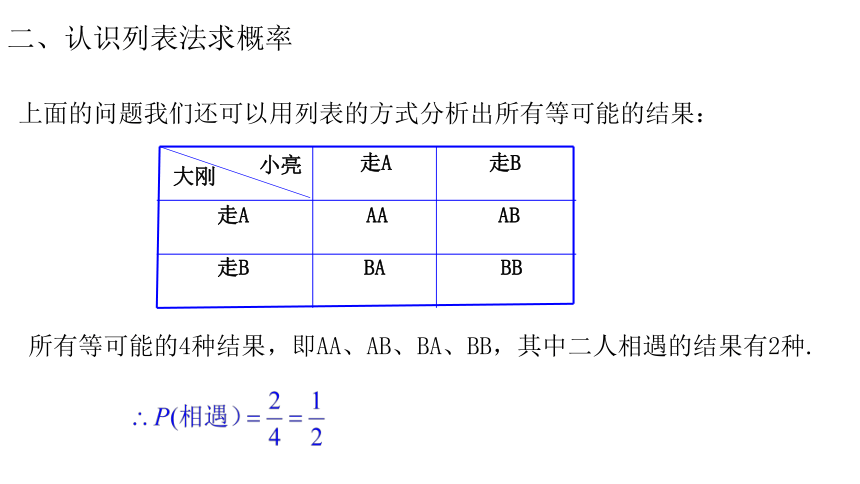
二、认识列表法求概率
上面的问题我们还可以用列表的方式分析出所有等可能的结果:
所有等可能的4种结果,即AA、AB、BA、BB,其中二人相遇的结果有2种.
大刚
小亮
AB
AA
BA
BB
走A
走B
走B
走A
例1 A,B两个盒子里各装入分别写有数字0,1的两张卡片,分别从每个盒子中随机取出1张卡片,两张卡片上的数字之积为0的概率是多少?
三、例题精讲
解:画树状图
从树状图可以看出,两张卡片上的数字之积共有4个等可能结果,从中可找出“两数之积为0”这一事件的结果有3个.
方法二:列表法
A
B
0
1
1
0
0
0
0
1
由上表可知,两张卡片上的数字之积共有4种等可能的结果,积为0的结果有3种.
例2 抛掷甲乙两只不透明的袋子里装有除颜色之外都相同的球,甲袋装有红、蓝、黄色球各一个,乙袋装有红、蓝色球各一个,从每个袋子里分别随机地摸出一个球,两个球恰为同色的概率是多少?
解: 从甲袋中随机摸出1个球,球的颜色有三个等可能的结果,从乙袋中随机摸出一个球,球的颜色有2个等可能的结果。从两个袋子中各摸出一个球,所有可能的结果可用树状图表示:
共有6个等可能结果,同色的有两个。
例3 同时掷两枚骰子,落定后,两枚骰子朝上一面的点数之和可能是哪些数?其中概率最大的是什么数?概率最小的是什么数?
如果画树状图,需要42个箭头,太麻烦,故用列表法较简单.
6 7 8 9 10 11 12
5 6 7 8 9 10 11
4 5 6 7 8 9 10
3 4 5 6 7 8 9
2 3 4 5 6 7 8
1 2 3 4 5 6 7
+ 1 2 3 4 5 6
解:列表如下:
由图表看出,点数之和为7的情况最多,有6种,概率最大.点数之和为2和12的情况最少,各1种,概率最小.
点数之和 2 3 4 5 6 7 8 9 10 11 12
小方格数 1 2 3 4 5 6 5 4 3 2 1
四、随堂练习
2.一个袋子中装有2个红球和2个绿球,任意摸出一球,记录颜色放回,再任意摸出一球,记录颜色放回,请你估计两次都摸到红球的概率是________.
1.某人有红、白、蓝三件衬衫和红、白、蓝三条长裤,该人任意拿一件衬衫和一条长裤,求正好是一套白色的概率_______.
9
1
4
1
4.经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,如果这三种可能性大小相同,当有三辆汽车经过这个十字路口时,求下列事件概率:
(1)三辆车全部继续直行;
(2)两辆车向右转,一辆车向左转;
(3)至少有两辆车向左转.
3.在6张卡片上分别写有1~6的整数,随机的抽取一张后放回,再随机的抽取一张,那么,第一次取出的数字能够整除第2次取出的数字的概是 .
左
右
直
第
一
辆
第
二
辆
第
三
辆
左直右
左
右
直
左
右
直
左
右
直
左直右
左直右
左直右
左直右
左直右
左直右
左直右
左直右
共有27种行驶方向
4、解:画树形图如下:
27
1
(
)
1
(
=
\
全部继续直行)
P
3
(
)
2
(
9
1
27
=
=
\
两车右转,一车左转)
P
5.小亮和大刚报名参加运动会100米比赛,预赛分A,B,C三组进行,运动员通过抽签决定参加那个小组,他们恰好分到一组的概率是多少?
小亮 大刚 抽到A组 抽到B组 抽到C组
抽到A组 AA AB AC
抽到B组 BA BB BC
抽到C组 CA CB CC
解:
3
1
9
3
(
=
=
同组)
P
1
答:他们恰好分到一组的概率是
3
·
6.甲、乙、丙三人打乒乓球.由哪两人先打呢 他们决定用 “石头、剪刀、布”的游戏来决定,游戏时三人每次做“石头” “剪刀”“布”三种手势中的一种,规定“石头” 胜“剪刀”, “剪刀”胜“布”, “布”胜“石头”. 问一次比赛能淘汰一人的概率是多少 (解析见下页)
7.用数字1,2,3,组成三位数,求其中恰有2个相同的数字的概率.
(解析见下页)
由规则可知,一次能淘汰一人的结果应是:“石石剪” “剪剪布” “布布石”三类. 由树形图可以看出,游戏的结果有27种,它们出现的可能性相等. 而满足条件(记为事件A)的结果有9种:
石
剪
布
石
游戏开始
甲
丙
乙
石
石
剪
布
石
剪
布
石
剪
布
石
剪
布
石
剪
布
石
剪
布
石
剪
布
石
剪
布
剪
布
石
剪
布
石
剪
布
剪
布
6、解:
1
2
3
1
组数开始
百位
个位
十位
1
2
3
1
2
3
1
2
3
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
7、解:
由树形图可以看出,所有可能的结果有27种,它们出现的可 能性相等.其中恰有2个数字相同的结果有18个。
五、挑战自我
下午放学后,小亮、小莹和大刚到学校兵乓球室去打乒乓球.当时只有一副空球桌,他们打算用“手心、手背”的方法决定哪两人先上场.游戏规则是:三人同时伸手心或手背,如果恰好其中有两人伸出的手势相同,那么这两人上场,否则重新开始.
假如这三个人每个人伸出手心或手背都是随机的,经过一次伸手试验,小亮上场的概率是多少
本课小结
利用树状图或表格可以清晰地表示出某个事件发生的所有可能出现的结果,从而较方便地求出某些事件发生的概率.
当试验包含两步时,列表法比较方便,当然,此时也可以用树状图法,当试验在三步或三步以上时,用画树状图法方便.
6.1 随机事件
第 6 章 事件的概率
6.7 利用画树状图和列表计算概率
教学目标
1、知识与能力:使学生在具体情境中了解概率的意义,能够运用一些方法计算简单的事件发生的概率,并阐述理由。
2、过程与方法:经历试验、列表、统计、计算、设计等活动,学生在具体情景中分析事件,计算其发生的概率。
3、情感、态度与价值观:通过丰富的数学活动,交流成功的经验,体验数学活动充满着探索和创造,体会数学的应用价值,培养积极思维的学习习惯。
新课导入
甲乙两村之间有A、B两条道路,小亮从甲村去往乙村,大刚从乙村去往甲村,二人同时出发。如果每人从A、B两条道路中随机选择一条,而且他们都不知道对方的选择,那么二人图途中相遇的概率是多少?
分析:这个问题与我们之前学过的问题有些不同,不能直接列出所有等可能的情况,那有没有不重不漏的列出所有结果的方法呢?我们今天就来研究下此类问题。
探究新知
一、认识树状图法求概率
思考问题
(1)小亮有几条路可以选择?随机选择一条路的可能性是相同?
(2)大刚有几条路可供选择?每条道路选中的可能性是否相同?
分析:由于小亮走道路A或B有两种可能,可画出同一点出发的两个箭头分别表示小亮走A或走B。当小亮走道路A时,由于大刚走道路A或B也有两种可能,所以在表示小亮走A的箭头前面再画出两个箭头,分别表示当小亮走道路A时大刚可能走道路A或道路B。同样地,在表示小亮走B的箭头前面再画出两个箭头,分别表示当小亮走道路B时,大刚可能揍道路A或道路B。
所有等可能性结果共有____种,
这四种情况有没有重复?
还有没有其他的没有列出的结果?其中两人相遇的情况有______种.
P(相遇)=_________
这种图像一棵横倒的树,我们叫它树状图.
四
二
AB(不相遇)
大刚
小亮
AA(相遇)
BA(不相遇)
BB(相遇)
走A
走B
走A
走B
走A
走B
AB(不相遇)
大刚
小亮
AA(相遇)
BA(不相遇)
BB(相遇)
走A
走B
走A
走B
走A
走B
小亮和大刚地位相同,也可表示如下:
所有等可能的结果共有4种:AA,AB,BA,BB,其中两人相遇的情况有2种,
所以,P(相遇)=
二、认识列表法求概率
上面的问题我们还可以用列表的方式分析出所有等可能的结果:
所有等可能的4种结果,即AA、AB、BA、BB,其中二人相遇的结果有2种.
大刚
小亮
AB
AA
BA
BB
走A
走B
走B
走A
例1 A,B两个盒子里各装入分别写有数字0,1的两张卡片,分别从每个盒子中随机取出1张卡片,两张卡片上的数字之积为0的概率是多少?
三、例题精讲
解:画树状图
从树状图可以看出,两张卡片上的数字之积共有4个等可能结果,从中可找出“两数之积为0”这一事件的结果有3个.
方法二:列表法
A
B
0
1
1
0
0
0
0
1
由上表可知,两张卡片上的数字之积共有4种等可能的结果,积为0的结果有3种.
例2 抛掷甲乙两只不透明的袋子里装有除颜色之外都相同的球,甲袋装有红、蓝、黄色球各一个,乙袋装有红、蓝色球各一个,从每个袋子里分别随机地摸出一个球,两个球恰为同色的概率是多少?
解: 从甲袋中随机摸出1个球,球的颜色有三个等可能的结果,从乙袋中随机摸出一个球,球的颜色有2个等可能的结果。从两个袋子中各摸出一个球,所有可能的结果可用树状图表示:
共有6个等可能结果,同色的有两个。
例3 同时掷两枚骰子,落定后,两枚骰子朝上一面的点数之和可能是哪些数?其中概率最大的是什么数?概率最小的是什么数?
如果画树状图,需要42个箭头,太麻烦,故用列表法较简单.
6 7 8 9 10 11 12
5 6 7 8 9 10 11
4 5 6 7 8 9 10
3 4 5 6 7 8 9
2 3 4 5 6 7 8
1 2 3 4 5 6 7
+ 1 2 3 4 5 6
解:列表如下:
由图表看出,点数之和为7的情况最多,有6种,概率最大.点数之和为2和12的情况最少,各1种,概率最小.
点数之和 2 3 4 5 6 7 8 9 10 11 12
小方格数 1 2 3 4 5 6 5 4 3 2 1
四、随堂练习
2.一个袋子中装有2个红球和2个绿球,任意摸出一球,记录颜色放回,再任意摸出一球,记录颜色放回,请你估计两次都摸到红球的概率是________.
1.某人有红、白、蓝三件衬衫和红、白、蓝三条长裤,该人任意拿一件衬衫和一条长裤,求正好是一套白色的概率_______.
9
1
4
1
4.经过某十字路口的汽车,它可能继续直行,也可能向左转或向右转,如果这三种可能性大小相同,当有三辆汽车经过这个十字路口时,求下列事件概率:
(1)三辆车全部继续直行;
(2)两辆车向右转,一辆车向左转;
(3)至少有两辆车向左转.
3.在6张卡片上分别写有1~6的整数,随机的抽取一张后放回,再随机的抽取一张,那么,第一次取出的数字能够整除第2次取出的数字的概是 .
左
右
直
第
一
辆
第
二
辆
第
三
辆
左直右
左
右
直
左
右
直
左
右
直
左直右
左直右
左直右
左直右
左直右
左直右
左直右
左直右
共有27种行驶方向
4、解:画树形图如下:
27
1
(
)
1
(
=
\
全部继续直行)
P
3
(
)
2
(
9
1
27
=
=
\
两车右转,一车左转)
P
5.小亮和大刚报名参加运动会100米比赛,预赛分A,B,C三组进行,运动员通过抽签决定参加那个小组,他们恰好分到一组的概率是多少?
小亮 大刚 抽到A组 抽到B组 抽到C组
抽到A组 AA AB AC
抽到B组 BA BB BC
抽到C组 CA CB CC
解:
3
1
9
3
(
=
=
同组)
P
1
答:他们恰好分到一组的概率是
3
·
6.甲、乙、丙三人打乒乓球.由哪两人先打呢 他们决定用 “石头、剪刀、布”的游戏来决定,游戏时三人每次做“石头” “剪刀”“布”三种手势中的一种,规定“石头” 胜“剪刀”, “剪刀”胜“布”, “布”胜“石头”. 问一次比赛能淘汰一人的概率是多少 (解析见下页)
7.用数字1,2,3,组成三位数,求其中恰有2个相同的数字的概率.
(解析见下页)
由规则可知,一次能淘汰一人的结果应是:“石石剪” “剪剪布” “布布石”三类. 由树形图可以看出,游戏的结果有27种,它们出现的可能性相等. 而满足条件(记为事件A)的结果有9种:
石
剪
布
石
游戏开始
甲
丙
乙
石
石
剪
布
石
剪
布
石
剪
布
石
剪
布
石
剪
布
石
剪
布
石
剪
布
石
剪
布
剪
布
石
剪
布
石
剪
布
剪
布
6、解:
1
2
3
1
组数开始
百位
个位
十位
1
2
3
1
2
3
1
2
3
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
1
2
3
7、解:
由树形图可以看出,所有可能的结果有27种,它们出现的可 能性相等.其中恰有2个数字相同的结果有18个。
五、挑战自我
下午放学后,小亮、小莹和大刚到学校兵乓球室去打乒乓球.当时只有一副空球桌,他们打算用“手心、手背”的方法决定哪两人先上场.游戏规则是:三人同时伸手心或手背,如果恰好其中有两人伸出的手势相同,那么这两人上场,否则重新开始.
假如这三个人每个人伸出手心或手背都是随机的,经过一次伸手试验,小亮上场的概率是多少
本课小结
利用树状图或表格可以清晰地表示出某个事件发生的所有可能出现的结果,从而较方便地求出某些事件发生的概率.
当试验包含两步时,列表法比较方便,当然,此时也可以用树状图法,当试验在三步或三步以上时,用画树状图法方便.
