湘教版七年级下册2.2乘法公式 知识点分类练习题(含解析)
文档属性
| 名称 | 湘教版七年级下册2.2乘法公式 知识点分类练习题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 226.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-07 00:00:00 | ||
图片预览


文档简介
2022-2023学年湘教版七年级数学下册《2.2乘法公式》知识点分类练习题(附答案)
一.平方差公式
1.下列多项式乘以多项式能用平方差公式计算的是( )
A.(a+b)(﹣b﹣a) B.(﹣a+b)(﹣b﹣a)
C.(a+b)(b+a) D.(﹣a+b)(b﹣a)
2.若a+b=6,a2﹣b2=30,则a﹣b=( )
A.5 B.6 C.10 D.15
3.如果一个正整数能表示为两个连续奇数的平方差,那么称这个正整数为“创新数”,如8=32﹣12,16=52﹣32,所以8,16都是“创新数”,下列整数是“创新数”的是( )
A.20 B.22 C.26 D.24
4.同学们,我们以前学过乘法公式,你一定熟练掌握了吧!想办法计算:(1﹣)(1﹣)(1﹣)(1﹣)…(1﹣).
5.若a=20210,b=2020×2022﹣20212,c=()2020×()2021,则a,b,c的大小关系是( )
A.a<b<c B.b<a<c C.c<b<a D.b<c<a
6.(3+2)×(32+22)×(34+24)×(38+28)计算结果等于( )
A.1 B.316﹣216 C.332+232 D.332﹣232
7.观察:(x﹣1)(x+1)=x2﹣1,(x﹣1)(x2+x+1)=x3﹣1,(x﹣1)(x3+x2+x+1)=x4﹣1,据此规律,当(x﹣1)(x5+x4+x3+x2+x+1)=0时,代数式x2021﹣1的值为( )
A.1 B.0 C.1或﹣1 D.0或﹣2
8.计算:.
9.计算:(x﹣2y+3)(x+2y﹣3).
二.平方差公式的几何背景
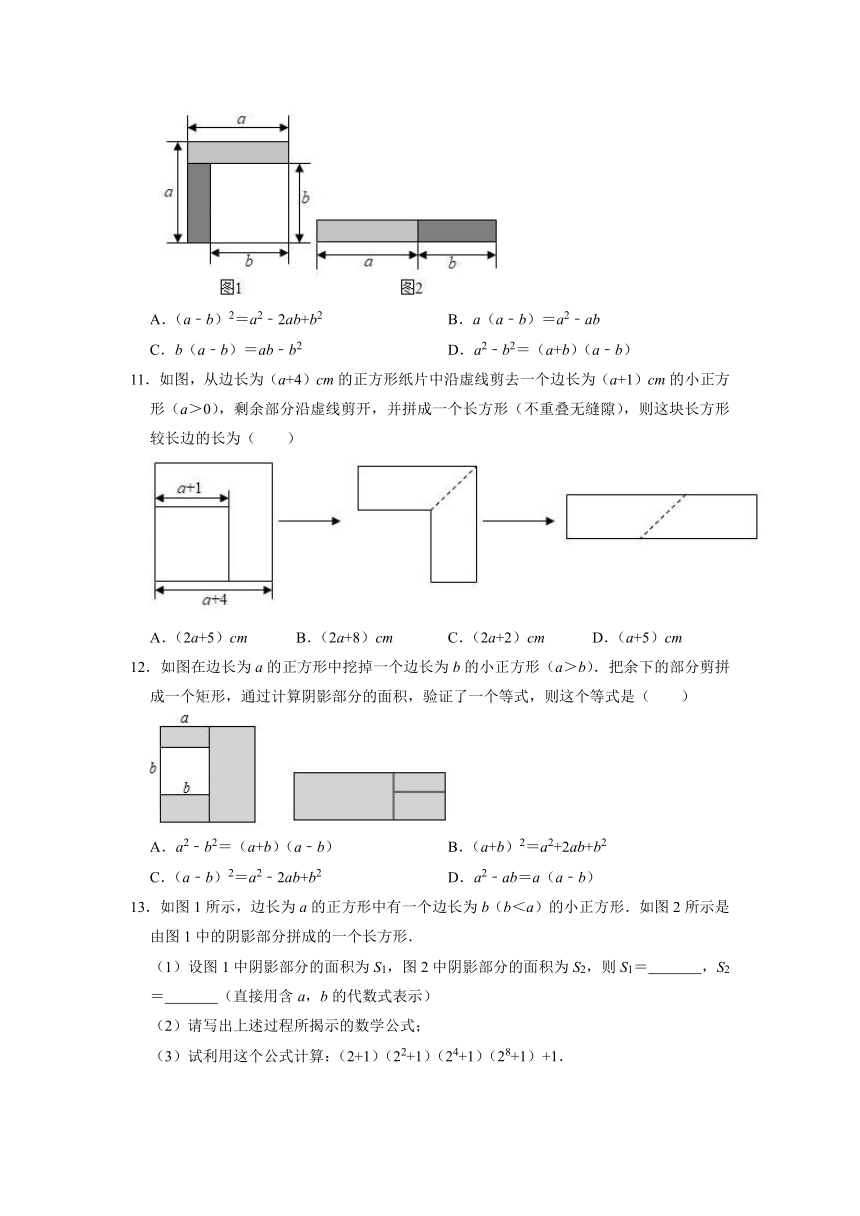
10.从边长为a的正方形中剪掉一个边长为b的正方形(如图1所示),然后将剩余部分拼成一个长方形(如图2所示).根据图形的变化过程,写出的一个正确的等式是( )
A.(a﹣b)2=a2﹣2ab+b2 B.a(a﹣b)=a2﹣ab
C.b(a﹣b)=ab﹣b2 D.a2﹣b2=(a+b)(a﹣b)
11.如图,从边长为(a+4)cm的正方形纸片中沿虚线剪去一个边长为(a+1)cm的小正方形(a>0),剩余部分沿虚线剪开,并拼成一个长方形(不重叠无缝隙),则这块长方形较长边的长为( )
A.(2a+5)cm B.(2a+8)cm C.(2a+2)cm D.(a+5)cm
12.如图在边长为a的正方形中挖掉一个边长为b的小正方形(a>b).把余下的部分剪拼成一个矩形,通过计算阴影部分的面积,验证了一个等式,则这个等式是( )
A.a2﹣b2=(a+b)(a﹣b) B.(a+b)2=a2+2ab+b2
C.(a﹣b)2=a2﹣2ab+b2 D.a2﹣ab=a(a﹣b)
13.如图1所示,边长为a的正方形中有一个边长为b(b<a)的小正方形.如图2所示是由图1中的阴影部分拼成的一个长方形.
(1)设图1中阴影部分的面积为S1,图2中阴影部分的面积为S2,则S1= ,S2= (直接用含a,b的代数式表示)
(2)请写出上述过程所揭示的数学公式;
(3)试利用这个公式计算:(2+1)(22+1)(24+1)(28+1)+1.
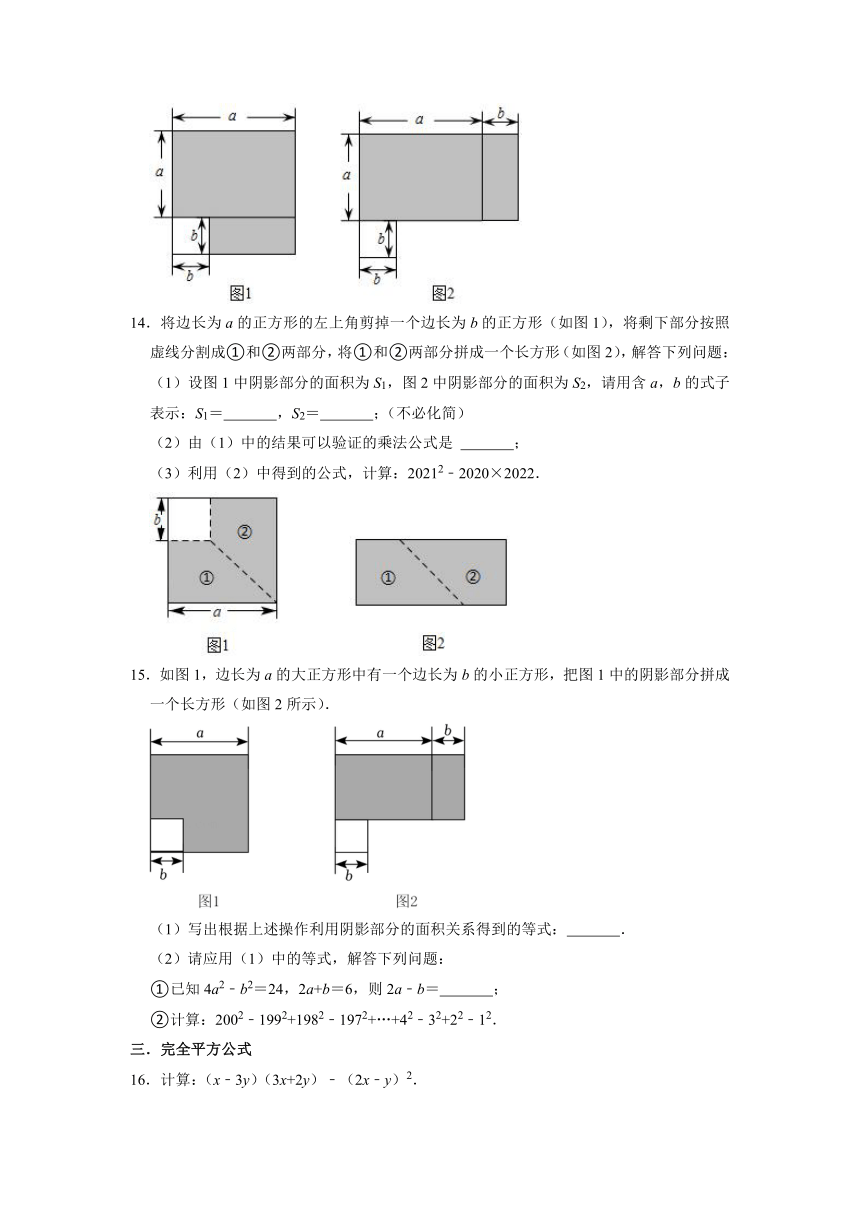
14.将边长为a的正方形的左上角剪掉一个边长为b的正方形(如图1),将剩下部分按照虚线分割成①和②两部分,将①和②两部分拼成一个长方形(如图2),解答下列问题:
(1)设图1中阴影部分的面积为S1,图2中阴影部分的面积为S2,请用含a,b的式子表示:S1= ,S2= ;(不必化简)
(2)由(1)中的结果可以验证的乘法公式是 ;
(3)利用(2)中得到的公式,计算:20212﹣2020×2022.
15.如图1,边长为a的大正方形中有一个边长为b的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示).
(1)写出根据上述操作利用阴影部分的面积关系得到的等式: .
(2)请应用(1)中的等式,解答下列问题:
①已知4a2﹣b2=24,2a+b=6,则2a﹣b= ;
②计算:2002﹣1992+1982﹣1972+…+42﹣32+22﹣12.
三.完全平方公式
16.计算:(x﹣3y)(3x+2y)﹣(2x﹣y)2.
17.若(x﹣2)2=x2+mx+n,则m,n的值分别是( )
A.4,4 B.﹣4,4 C.﹣4,﹣4 D.4,﹣4
18.(2a﹣m)2=4a2+2a+,则m=( )
A. B. C. D.
19.已知(x﹣p)2=x2+mx+36,则m= .
20.若(x﹣)2展开后等于x2+ax+,则a的值为 .
21.如果x+y=﹣5,xy=6,那么x2+y2= .
22.设(2a+b)2=(2a﹣b)2+A,则A= .
23.已知:a+b=5,(a﹣b)2=13,则ab的值是 .
24.已知(a﹣2019)2+(2020﹣a)2=2021,则(a﹣2019)(a﹣2020)= .
25.贾宪三角在历史上被不同时代的人绘制出来,有着不同的应用指向.如图,在贾宪三角中,第三行的三个数(1,2,1)对应着两数和的平方(a+b)2的展开式a2+2ab+b2的系数,类似地,通过计算可以发现:第四行的四个数(1,3,3,1)对应着两数和的立方(a+b)3的展开式a3+3a2b+3ab2+b3的系数,第五行的五个数(1,4,6,4,1)对应着两数和的四次方(a+b)4的展开式a4+4a3b+6a2b2+4ab3+b4的系数,等等.由此可见,贾宪三角可以看作是对两数和平方公式的推广.此图揭示了(a+b)n(n为非负整数)的展开式的项数及各项系数的有关规律.根据此规律,(a+b)6的展开式中字母a、b指数相同的项为 .
四.完全平方公式的几何背景
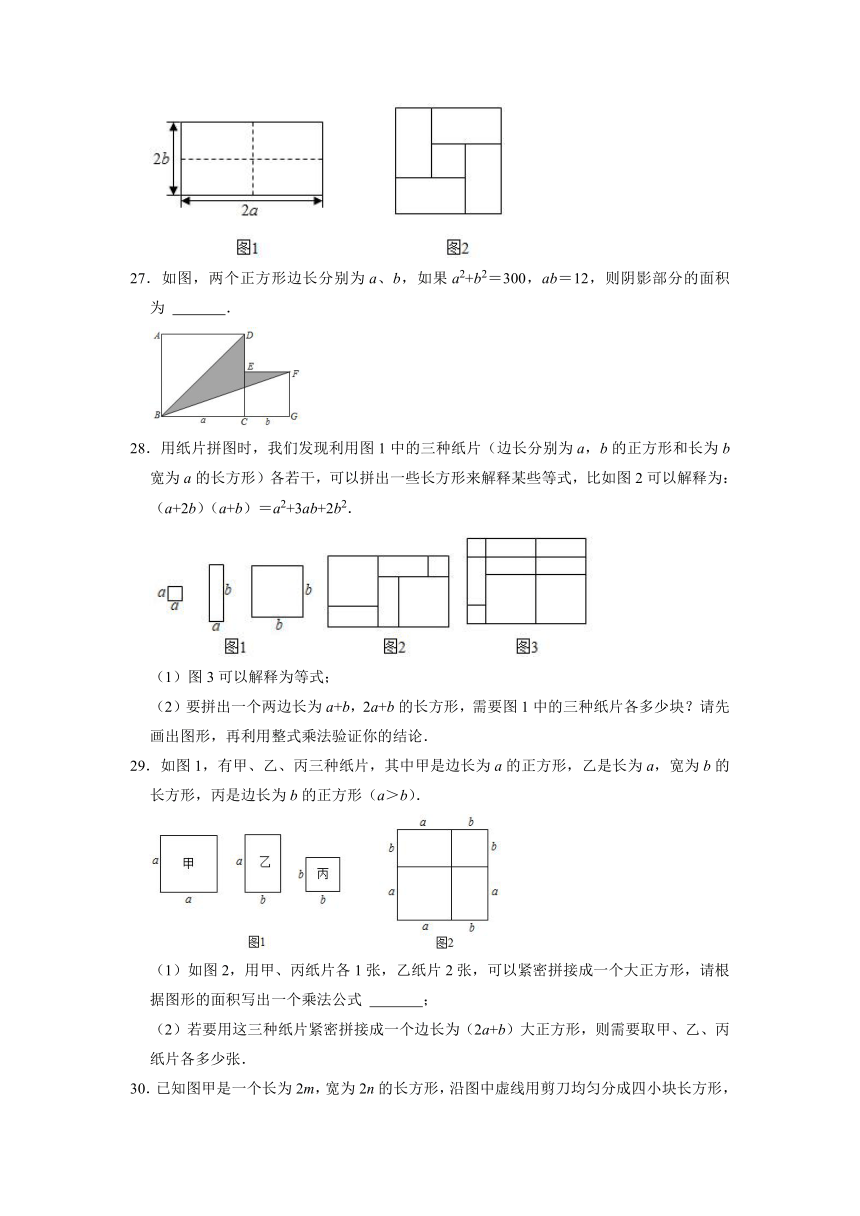
26.将一个长为2a,宽为2b的矩形纸片(a>b),用剪刀沿图1中的虚线剪开,分成四块形状和大小都一样的小矩形纸片,然后按图2的方式拼成一个正方形,则中间小正方形的面积为 .
27.如图,两个正方形边长分别为a、b,如果a2+b2=300,ab=12,则阴影部分的面积为 .
28.用纸片拼图时,我们发现利用图1中的三种纸片(边长分别为a,b的正方形和长为b宽为a的长方形)各若干,可以拼出一些长方形来解释某些等式,比如图2可以解释为:(a+2b)(a+b)=a2+3ab+2b2.
(1)图3可以解释为等式;
(2)要拼出一个两边长为a+b,2a+b的长方形,需要图1中的三种纸片各多少块?请先画出图形,再利用整式乘法验证你的结论.
29.如图1,有甲、乙、丙三种纸片,其中甲是边长为a的正方形,乙是长为a,宽为b的长方形,丙是边长为b的正方形(a>b).
(1)如图2,用甲、丙纸片各1张,乙纸片2张,可以紧密拼接成一个大正方形,请根据图形的面积写出一个乘法公式 ;
(2)若要用这三种纸片紧密拼接成一个边长为(2a+b)大正方形,则需要取甲、乙、丙纸片各多少张.
30.已知图甲是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均匀分成四小块长方形,然后按图乙的形状拼成一个正方形.
(1)你认为图乙中阴影部分的正方形的边长等于多少?
(2)请用两种不同的方法求图乙中阴影部分的面积.
(3)观察图乙,你能写出下列三个代数式之间的等量关系吗?
(m+n)2、(m﹣n)2、mn.
(4)根据(3)题中的等量关系,解决如下问题:若a+b=6,ab=3,求(a﹣b)2的值.
31.如图1在一个长为2a,宽为2b的长方形图中,沿着虚线用剪刀均分成4块小长方形,然后按图2的形状拼成一个正方形.
(1)图2中阴影部分的正方形边长为 .
(2)请你用两种不同的方法表示图2中阴影部分的面积,并用等式表示.
(3)如图3,点C是线段AB上的一点,以AC,BC为边向两边作正方形,面积分别是S1和S2,设AB=8,两正方形的面积和S1+S2=34,求图中阴影部分面积.
32.两个边长分别为a和b的正方形如图放置(图1),其未叠合部分(阴影)面积为S1;若再在图1中大正方形的右下角摆放一个边长为b的小正方形(如图2),两个小正方形叠合部分(阴影)面积为S2.
(1)用含a,b的代数式分别表示S1、S2;
(2)若a+b=10,ab=20,求S1+S2的值;
(3)当S1+S2=30时,求出图3中阴影部分的面积S3.
33.完全平方公式:(a±b)2=a2±2ab+b2适当的变形,可以解决很多的数学问题.
例如:若a+b=3,ab=1,求a2+b2的值.
解:因为a+b=3,ab=1,
所以(a+b)2=9,2ab=2.
所以a2+b2+2ab=9,得a2+b2=7.
根据上面的解题思路与方法,解决下列问题:
(1)若x+y=8,x2+y2=30,求xy的值;
(2)请直接写出下列问题答案:
①若(4﹣x)x=3,则(4﹣x)2+x2= ;
②若(3﹣x)(5﹣x)=6,则(3﹣x)2+(5﹣x)2= .
(3)如图,点C是线段AB上的一点,以AC,BC为边向两边作正方形,设AB=10,两正方形的面积和S1+S2=52,求图中阴影部分面积.
五.完全平方式
34.若多项式4x2+kx+25是完全平方式,则k的值是 .
35.若x2﹣(m﹣1)x+49是完全平方式,则实数m= .
36.若多项式x2+4x﹣m是一个完全平方式,则m= .
37.若x2﹣2(a+1)xy+9y2是完全平方式,则实数a的值是 .
参考答案
一.平方差公式
1.解:能用平方差公式计算的是(﹣a+b)(﹣b﹣a),其它的不能用平方差公式计算.
故选:B.
2.解:∵a+b=6,a2﹣b2=30,
∴(a+b)(a﹣b)=30,
∴a﹣b=30÷6=5,
故选:A.
3.解:设两个连续奇数是2n﹣1和2n+1(其中n取正整数),
∵(2n+1)2﹣(2n﹣1)2=(2n+1+2n﹣1)(2n+1﹣2n+1)=4n 2=8n,
∴由这两个连续奇数构造的奇特数是8的倍数.
∵20、22、26都不是8的倍数,
∴它们不是“创新数”,
∵24是8的倍数,
∴24是“创新数”,且24=72﹣52,
故选:D.
4.解:原式=(1+)×(1﹣)×(1+)×(1﹣)×(1+)×(1﹣)+...+(1+)×(1﹣)
=
=
=.
5.解:a=20210=1;
b=2020×2022﹣20212
=(2021﹣1)×(2021+1)﹣20212
=20212﹣1﹣20212
=﹣1;
c=(﹣)2020×()2021
=(﹣×)2020×
=;
∴b<a<c.
故选:B.
6.解:(3+2)×(32+22)×(34+24)×(38+28)
=(3﹣2)(3+2)×(32+22)×(34+24)×(38+28)
=(32﹣22)×(32+22)×(34+24)×(38+28)
=(34﹣24)×(34+24)×(38+28)
=(38﹣28)×(38+28)
=316﹣216.
故选:B.
7.解:∵(x﹣1)(x5+x4+x3+x2+x+1)=0.
∴x6﹣1=0.
∴x6=1.
∴(x3)2=1.
∴x3=±1.
∴x=±1.
当x=1时,原式=12021﹣1=0.
当x=﹣1时,原式=12021﹣1=﹣2.
故选:D.
8.解:原式=
=
=2022.
9.解:原式=x2﹣(2y﹣3)2
=x2﹣(4y2﹣12y+9)
=x2﹣4y2+12y﹣9.
二.平方差公式的几何背景
10.解:根据图1和图2可得阴影部分的面积为:a2﹣b2和(a+b)(a﹣b),
∴a2﹣b2=(a+b)(a﹣b),
故选:D.
11.解:由题意得,所剪梯形的两底各为a+4和a+1,
∴该长方形较长边的长为:
(a+4)+(a+1)=a+4+a+1=2a+5,
故选:A.
12.解:由图可知,大正方形减小正方形剩下的部分面积为a2﹣b2;
拼成的长方形的面积:(a+b)×(a﹣b),
所以得出:a2﹣b2=(a+b)(a﹣b),
故选:A.
13.解:(1)由图1可表示阴影部分的面积为:a2﹣b2,
由图2可表示阴影部分的面积为:(a+b)(a﹣b),
故答案为:a2﹣b2,(a+b)(a﹣b);
(2)由(1)结果可得公式:a2﹣b2=(a+b)(a﹣b)或(a+b)(a﹣b)=a2﹣b2;
(3)利用(2)题结论可得,
(2+1)(22+1)(24+1)(28+1)+1=
(2﹣1)(2+1)(22+1)(24+1)(28+1)+1
=(22﹣1)(22+1)(24+1)(28+1)+1
=(24﹣1)(24+1)(28+1)
=(28﹣1)(28+1)+1
=216﹣1+1
=216.
14.解:(1)由题意得,S1=a2﹣b2,S2=(a+b)(a﹣b),
故答案为:a2﹣b2,(a+b)(a﹣b);
(2)由(1)中的结果可验证的乘法公式为(a+b)(a﹣b)=a2﹣b2,
故答案为:(a+b)(a﹣b)=a2﹣b2;
(3)由(2)中所得乘法公式(a+b)(a﹣b)=a2﹣b2可得,
20212﹣2020×2022=20212﹣(2021+1)(2021﹣1)=20212﹣(20212﹣1)
=20212﹣20212+1
=1.
15.解:(1)根据上述操作利用阴影部分的面积关系得到的等式:a2﹣b2=(a+b)(a﹣b),
故答案为:a2﹣b2=(a+b)(a﹣b);
(2)①∵4a2﹣b2=24,
∴(2a+b)(2a﹣b)=24,
∵2a+b=6,
∴2a﹣b=4,
故答案为:4,
②2002﹣1992+1982﹣1972+…+42﹣32+22﹣12
=(200+199)(200﹣199)+(198+197)(198﹣197)+...+(4+3)(4﹣3)+(2+1)(2﹣1)
=200+199+198+197+...+4+3+2+1
=×(200+1)×200
=20100.
三.完全平方公式
16.解:(x﹣3y)(3x+2y)﹣(2x﹣y)2
=3x2+2xy﹣9xy﹣6y2﹣(4x2﹣4xy+y2)
=3x2+2xy﹣9xy﹣6y2﹣4x2+4xy﹣y2
=﹣x2﹣3xy﹣7y2.
17.解:∵(x﹣2)2=x2﹣4x+4,(x﹣2)2=x2+mx+n,
∴x2﹣4x+4=x2+mx+n,
∴m=﹣4,n=4.
故选:B.
18.解:∵(2a﹣m)2=4a2﹣4ma+m2,(2a﹣m)2=4a2+2a+,
∴4a2﹣4ma+m2=4a2+2a+,
∴﹣4m=2,
解得:m=﹣,
故选:D.
19.解:因为(x﹣p)2=x2﹣2px+p2,(x﹣p)2=x2+mx+36,
所以m=﹣2p,p2=36,
所以m=﹣2p,p=±6,
所以m=﹣12或12.
故答案为:﹣12或12.
20.解:根据题意,可得:
(x﹣)2=x2+ax+,
∵(x﹣)2=x2﹣x+,
∴x2﹣x+=x2+ax+,
∴a=﹣1.
故答案为:﹣1.
21.解:由完全平方公式(a+b)2=a2+2ab+b2,
可得a2+b2=(a+b)2﹣2ab,
∴当x+y=﹣5,xy=6时,
x2+y2=(﹣5)2﹣2×6=25﹣12=13,
故答案为:13.
22.解:因为(2a+b)2=(2a﹣b)2+A,(2a+b)2=(2a﹣b)2+8ab,
所以A=8ab.
故答案为:8ab.
23.解:∵a+b=5,(a﹣b)2=13,
∴a2+b2+2ab=25①,a2+b2﹣2ab=13②,
则①﹣②可得:4ab=12,
所以ab=3.
故答案为:3.
24.解:设a﹣2019=x,2020﹣a=y,则x+y=1,
∵(a﹣2019)2+(2020﹣a)2=2021,
∴x2+y2=2021,
∵(x+y)2=x2+2xy+y2,
∴2xy=(x+y)2﹣(x2+y2)=1﹣2021=﹣2020,
即xy=﹣1010,
∴(a﹣2019)(2020﹣a)=xy=﹣1010,
∴(a﹣2019)(a﹣2020)
=﹣(a﹣2019)(2020﹣a)
=﹣xy
=1010.
故答案为:1010.
25.解:根据规律直接写出(a+b)6=a6+6a5b+15a4b2+20a3b3+15a2b3+6ab4+b5,
所以(a+b)6的展开式中字母a、b指数相同的项为20a3b3.
故答案为:20a3b3.
四.完全平方公式的几何背景
26.解:由拼图可得小正方形的边长是小矩形长与宽的差,
即a﹣b,
∴中间小正方形的面积为(a﹣b)2.
故答案应为:(a﹣b)2.
27.解:∵a2+b2=300,ab=12,
∴=
==144.
故答案为:144.
28.解:(1)∵图3面积为(a+2b)(2a+b)=2a2+5ab+2b2,
∴图3可以解释为等式(a+2b)(2a+b)=2a2+5ab+2b2.
(2)需要边长为a的正方形2块,长为b宽为a的长方形3块,边长为b的正方形1块.如下图所示:
整式乘法验证,(a+b)(2a+b)=2a2+ab+2ab+b2=2a2+3ab+b2,
∴需要a×a的正方形2块,需要a×b的长方形3块,需要b×b的正方形1块.
29.解:(1)∵图2中正方形的面积可表示为:(a+b)2和a2+2ab+b2,
∴可得公式(a+b)2=a2+2ab+b2,
故答案为:(a+b)2=a2+2ab+b2;
(2)由计算(2a+b)2=4a2+4ab+b2可得,
需要取甲种纸片4张、乙种纸片4张、丙种纸片1张.
30.解:(1)由题意得,图乙中阴影部分的正方形的边长等于m﹣n;
(2)图乙中阴影部分的面积可表示为:(m+n)2﹣4mn或(m﹣n)2;
(3)由图乙中阴影部分的面积可得等式:(m+n)2﹣4mn=(m﹣n)2;
(4)由(3)题结果(m+n)2﹣4mn=(m﹣n)2可得,
(a﹣b)2=(a+b)2﹣4ab,
∴当a+b=6,ab=3时,
(a﹣b)2=62﹣4×3=36﹣12=24,
即:(a﹣b)2=24.
31.解:(1)由题意得:图2中阴影部分的正方形边长为:a﹣b.
故答案为:a﹣b.
(2)图2中阴影部分面积为:(a﹣b)2,还可以表示为:(a+b)2﹣4ab.
∴(a﹣b)2=(a+b)2﹣4ab.
(3)设AC=x,BC=y,由题意得:x+y=8,x2+y2=S1+S2=34.
∵(x+y)2=x2+y2+2xy.
∴64=34+2xy.
∴xy=15.
∴S阴影=AC CF=xy=7.5.
32.解:(1)由图可得,S1=a2﹣b2,
S2=a2﹣a(a﹣b)﹣b(a﹣b)﹣b(a﹣b)=2b2﹣ab;
(2)S1+S2=a2﹣b2+2b2﹣ab=a2+b2﹣ab,
∵a+b=10,ab=20,
∴S1+S2=a2+b2﹣ab=(a+b)2﹣3ab=100﹣3×20=40;
(3)由图可得,S3=a2+b2﹣b(a+b)﹣a2=(a2+b2﹣ab),
∵S1+S2=a2+b2﹣ab=30,
∴S3=×30=15.
33.解:(1)由完全平方公式(a+b)2=a2+2ab+b2得,ab=,
∴当x+y=8,x2+y2=30时,
xy====17;
(2)①由完全平方公式(a+b)2=a2+2ab+b2得,a2+b2=(a+b)2﹣2ab,
∴当(4﹣x)x=3时,
(4﹣x)2+x2=[(4﹣x)+x]2﹣2(4﹣x)x
=42﹣2×3
=16﹣6
=10,
故答案为:10;
②由完全平方公式(a﹣b)2=a2﹣2ab+b2得,a2+b2=(a﹣b)2+2ab,
∴当(3﹣x)(5﹣x)=6时,
(3﹣x)2+(5﹣x)2=[(3﹣x)﹣(5﹣x)]2+2(3﹣x)(5﹣x)=(﹣2)2+2×6=4+12=16,
故答案为:16;
(3)由完全平方公式(a+b)2=a2+2ab+b2得,=,
∴当AC+BC=AB=10,AC2+BC2=S1+S2=52时,
图中阴影部分面积======12.
五.完全平方式
34.解:∵4x2+kx+25是一个完全平方式,
∴4x2+kx+25=(2x)2+kx+52=(2x±5)2,
∵(2x±5)2=4x2±20x+25,
∴kx=±20x,解得k=±20.
故答案为:±20.
35.解:∵x2﹣(m﹣1)x+49是完全平方式,
∴﹣(m﹣1)=±14,
解得:m=15或﹣13.
故答案为:15或﹣13.
36.解:∵多项式x2+4x﹣m是一个完全平方式,
∴Δ=42﹣4×1×(﹣m)=0,
∴m=﹣4.
故答案为:﹣4.
37.解:∵x2﹣2(a+1)xy+9y2是完全平方式,x2﹣2(a+1)xy+9y2=x2﹣2(a+1)xy+(3y)2,
∴﹣2(a+1)xy=±2×x×3y,
解得a+1=±3,
∴a=2或a=﹣4.
故答案为:2或﹣4.
一.平方差公式
1.下列多项式乘以多项式能用平方差公式计算的是( )
A.(a+b)(﹣b﹣a) B.(﹣a+b)(﹣b﹣a)
C.(a+b)(b+a) D.(﹣a+b)(b﹣a)
2.若a+b=6,a2﹣b2=30,则a﹣b=( )
A.5 B.6 C.10 D.15
3.如果一个正整数能表示为两个连续奇数的平方差,那么称这个正整数为“创新数”,如8=32﹣12,16=52﹣32,所以8,16都是“创新数”,下列整数是“创新数”的是( )
A.20 B.22 C.26 D.24
4.同学们,我们以前学过乘法公式,你一定熟练掌握了吧!想办法计算:(1﹣)(1﹣)(1﹣)(1﹣)…(1﹣).
5.若a=20210,b=2020×2022﹣20212,c=()2020×()2021,则a,b,c的大小关系是( )
A.a<b<c B.b<a<c C.c<b<a D.b<c<a
6.(3+2)×(32+22)×(34+24)×(38+28)计算结果等于( )
A.1 B.316﹣216 C.332+232 D.332﹣232
7.观察:(x﹣1)(x+1)=x2﹣1,(x﹣1)(x2+x+1)=x3﹣1,(x﹣1)(x3+x2+x+1)=x4﹣1,据此规律,当(x﹣1)(x5+x4+x3+x2+x+1)=0时,代数式x2021﹣1的值为( )
A.1 B.0 C.1或﹣1 D.0或﹣2
8.计算:.
9.计算:(x﹣2y+3)(x+2y﹣3).
二.平方差公式的几何背景
10.从边长为a的正方形中剪掉一个边长为b的正方形(如图1所示),然后将剩余部分拼成一个长方形(如图2所示).根据图形的变化过程,写出的一个正确的等式是( )
A.(a﹣b)2=a2﹣2ab+b2 B.a(a﹣b)=a2﹣ab
C.b(a﹣b)=ab﹣b2 D.a2﹣b2=(a+b)(a﹣b)
11.如图,从边长为(a+4)cm的正方形纸片中沿虚线剪去一个边长为(a+1)cm的小正方形(a>0),剩余部分沿虚线剪开,并拼成一个长方形(不重叠无缝隙),则这块长方形较长边的长为( )
A.(2a+5)cm B.(2a+8)cm C.(2a+2)cm D.(a+5)cm
12.如图在边长为a的正方形中挖掉一个边长为b的小正方形(a>b).把余下的部分剪拼成一个矩形,通过计算阴影部分的面积,验证了一个等式,则这个等式是( )
A.a2﹣b2=(a+b)(a﹣b) B.(a+b)2=a2+2ab+b2
C.(a﹣b)2=a2﹣2ab+b2 D.a2﹣ab=a(a﹣b)
13.如图1所示,边长为a的正方形中有一个边长为b(b<a)的小正方形.如图2所示是由图1中的阴影部分拼成的一个长方形.
(1)设图1中阴影部分的面积为S1,图2中阴影部分的面积为S2,则S1= ,S2= (直接用含a,b的代数式表示)
(2)请写出上述过程所揭示的数学公式;
(3)试利用这个公式计算:(2+1)(22+1)(24+1)(28+1)+1.
14.将边长为a的正方形的左上角剪掉一个边长为b的正方形(如图1),将剩下部分按照虚线分割成①和②两部分,将①和②两部分拼成一个长方形(如图2),解答下列问题:
(1)设图1中阴影部分的面积为S1,图2中阴影部分的面积为S2,请用含a,b的式子表示:S1= ,S2= ;(不必化简)
(2)由(1)中的结果可以验证的乘法公式是 ;
(3)利用(2)中得到的公式,计算:20212﹣2020×2022.
15.如图1,边长为a的大正方形中有一个边长为b的小正方形,把图1中的阴影部分拼成一个长方形(如图2所示).
(1)写出根据上述操作利用阴影部分的面积关系得到的等式: .
(2)请应用(1)中的等式,解答下列问题:
①已知4a2﹣b2=24,2a+b=6,则2a﹣b= ;
②计算:2002﹣1992+1982﹣1972+…+42﹣32+22﹣12.
三.完全平方公式
16.计算:(x﹣3y)(3x+2y)﹣(2x﹣y)2.
17.若(x﹣2)2=x2+mx+n,则m,n的值分别是( )
A.4,4 B.﹣4,4 C.﹣4,﹣4 D.4,﹣4
18.(2a﹣m)2=4a2+2a+,则m=( )
A. B. C. D.
19.已知(x﹣p)2=x2+mx+36,则m= .
20.若(x﹣)2展开后等于x2+ax+,则a的值为 .
21.如果x+y=﹣5,xy=6,那么x2+y2= .
22.设(2a+b)2=(2a﹣b)2+A,则A= .
23.已知:a+b=5,(a﹣b)2=13,则ab的值是 .
24.已知(a﹣2019)2+(2020﹣a)2=2021,则(a﹣2019)(a﹣2020)= .
25.贾宪三角在历史上被不同时代的人绘制出来,有着不同的应用指向.如图,在贾宪三角中,第三行的三个数(1,2,1)对应着两数和的平方(a+b)2的展开式a2+2ab+b2的系数,类似地,通过计算可以发现:第四行的四个数(1,3,3,1)对应着两数和的立方(a+b)3的展开式a3+3a2b+3ab2+b3的系数,第五行的五个数(1,4,6,4,1)对应着两数和的四次方(a+b)4的展开式a4+4a3b+6a2b2+4ab3+b4的系数,等等.由此可见,贾宪三角可以看作是对两数和平方公式的推广.此图揭示了(a+b)n(n为非负整数)的展开式的项数及各项系数的有关规律.根据此规律,(a+b)6的展开式中字母a、b指数相同的项为 .
四.完全平方公式的几何背景
26.将一个长为2a,宽为2b的矩形纸片(a>b),用剪刀沿图1中的虚线剪开,分成四块形状和大小都一样的小矩形纸片,然后按图2的方式拼成一个正方形,则中间小正方形的面积为 .
27.如图,两个正方形边长分别为a、b,如果a2+b2=300,ab=12,则阴影部分的面积为 .
28.用纸片拼图时,我们发现利用图1中的三种纸片(边长分别为a,b的正方形和长为b宽为a的长方形)各若干,可以拼出一些长方形来解释某些等式,比如图2可以解释为:(a+2b)(a+b)=a2+3ab+2b2.
(1)图3可以解释为等式;
(2)要拼出一个两边长为a+b,2a+b的长方形,需要图1中的三种纸片各多少块?请先画出图形,再利用整式乘法验证你的结论.
29.如图1,有甲、乙、丙三种纸片,其中甲是边长为a的正方形,乙是长为a,宽为b的长方形,丙是边长为b的正方形(a>b).
(1)如图2,用甲、丙纸片各1张,乙纸片2张,可以紧密拼接成一个大正方形,请根据图形的面积写出一个乘法公式 ;
(2)若要用这三种纸片紧密拼接成一个边长为(2a+b)大正方形,则需要取甲、乙、丙纸片各多少张.
30.已知图甲是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均匀分成四小块长方形,然后按图乙的形状拼成一个正方形.
(1)你认为图乙中阴影部分的正方形的边长等于多少?
(2)请用两种不同的方法求图乙中阴影部分的面积.
(3)观察图乙,你能写出下列三个代数式之间的等量关系吗?
(m+n)2、(m﹣n)2、mn.
(4)根据(3)题中的等量关系,解决如下问题:若a+b=6,ab=3,求(a﹣b)2的值.
31.如图1在一个长为2a,宽为2b的长方形图中,沿着虚线用剪刀均分成4块小长方形,然后按图2的形状拼成一个正方形.
(1)图2中阴影部分的正方形边长为 .
(2)请你用两种不同的方法表示图2中阴影部分的面积,并用等式表示.
(3)如图3,点C是线段AB上的一点,以AC,BC为边向两边作正方形,面积分别是S1和S2,设AB=8,两正方形的面积和S1+S2=34,求图中阴影部分面积.
32.两个边长分别为a和b的正方形如图放置(图1),其未叠合部分(阴影)面积为S1;若再在图1中大正方形的右下角摆放一个边长为b的小正方形(如图2),两个小正方形叠合部分(阴影)面积为S2.
(1)用含a,b的代数式分别表示S1、S2;
(2)若a+b=10,ab=20,求S1+S2的值;
(3)当S1+S2=30时,求出图3中阴影部分的面积S3.
33.完全平方公式:(a±b)2=a2±2ab+b2适当的变形,可以解决很多的数学问题.
例如:若a+b=3,ab=1,求a2+b2的值.
解:因为a+b=3,ab=1,
所以(a+b)2=9,2ab=2.
所以a2+b2+2ab=9,得a2+b2=7.
根据上面的解题思路与方法,解决下列问题:
(1)若x+y=8,x2+y2=30,求xy的值;
(2)请直接写出下列问题答案:
①若(4﹣x)x=3,则(4﹣x)2+x2= ;
②若(3﹣x)(5﹣x)=6,则(3﹣x)2+(5﹣x)2= .
(3)如图,点C是线段AB上的一点,以AC,BC为边向两边作正方形,设AB=10,两正方形的面积和S1+S2=52,求图中阴影部分面积.
五.完全平方式
34.若多项式4x2+kx+25是完全平方式,则k的值是 .
35.若x2﹣(m﹣1)x+49是完全平方式,则实数m= .
36.若多项式x2+4x﹣m是一个完全平方式,则m= .
37.若x2﹣2(a+1)xy+9y2是完全平方式,则实数a的值是 .
参考答案
一.平方差公式
1.解:能用平方差公式计算的是(﹣a+b)(﹣b﹣a),其它的不能用平方差公式计算.
故选:B.
2.解:∵a+b=6,a2﹣b2=30,
∴(a+b)(a﹣b)=30,
∴a﹣b=30÷6=5,
故选:A.
3.解:设两个连续奇数是2n﹣1和2n+1(其中n取正整数),
∵(2n+1)2﹣(2n﹣1)2=(2n+1+2n﹣1)(2n+1﹣2n+1)=4n 2=8n,
∴由这两个连续奇数构造的奇特数是8的倍数.
∵20、22、26都不是8的倍数,
∴它们不是“创新数”,
∵24是8的倍数,
∴24是“创新数”,且24=72﹣52,
故选:D.
4.解:原式=(1+)×(1﹣)×(1+)×(1﹣)×(1+)×(1﹣)+...+(1+)×(1﹣)
=
=
=.
5.解:a=20210=1;
b=2020×2022﹣20212
=(2021﹣1)×(2021+1)﹣20212
=20212﹣1﹣20212
=﹣1;
c=(﹣)2020×()2021
=(﹣×)2020×
=;
∴b<a<c.
故选:B.
6.解:(3+2)×(32+22)×(34+24)×(38+28)
=(3﹣2)(3+2)×(32+22)×(34+24)×(38+28)
=(32﹣22)×(32+22)×(34+24)×(38+28)
=(34﹣24)×(34+24)×(38+28)
=(38﹣28)×(38+28)
=316﹣216.
故选:B.
7.解:∵(x﹣1)(x5+x4+x3+x2+x+1)=0.
∴x6﹣1=0.
∴x6=1.
∴(x3)2=1.
∴x3=±1.
∴x=±1.
当x=1时,原式=12021﹣1=0.
当x=﹣1时,原式=12021﹣1=﹣2.
故选:D.
8.解:原式=
=
=2022.
9.解:原式=x2﹣(2y﹣3)2
=x2﹣(4y2﹣12y+9)
=x2﹣4y2+12y﹣9.
二.平方差公式的几何背景
10.解:根据图1和图2可得阴影部分的面积为:a2﹣b2和(a+b)(a﹣b),
∴a2﹣b2=(a+b)(a﹣b),
故选:D.
11.解:由题意得,所剪梯形的两底各为a+4和a+1,
∴该长方形较长边的长为:
(a+4)+(a+1)=a+4+a+1=2a+5,
故选:A.
12.解:由图可知,大正方形减小正方形剩下的部分面积为a2﹣b2;
拼成的长方形的面积:(a+b)×(a﹣b),
所以得出:a2﹣b2=(a+b)(a﹣b),
故选:A.
13.解:(1)由图1可表示阴影部分的面积为:a2﹣b2,
由图2可表示阴影部分的面积为:(a+b)(a﹣b),
故答案为:a2﹣b2,(a+b)(a﹣b);
(2)由(1)结果可得公式:a2﹣b2=(a+b)(a﹣b)或(a+b)(a﹣b)=a2﹣b2;
(3)利用(2)题结论可得,
(2+1)(22+1)(24+1)(28+1)+1=
(2﹣1)(2+1)(22+1)(24+1)(28+1)+1
=(22﹣1)(22+1)(24+1)(28+1)+1
=(24﹣1)(24+1)(28+1)
=(28﹣1)(28+1)+1
=216﹣1+1
=216.
14.解:(1)由题意得,S1=a2﹣b2,S2=(a+b)(a﹣b),
故答案为:a2﹣b2,(a+b)(a﹣b);
(2)由(1)中的结果可验证的乘法公式为(a+b)(a﹣b)=a2﹣b2,
故答案为:(a+b)(a﹣b)=a2﹣b2;
(3)由(2)中所得乘法公式(a+b)(a﹣b)=a2﹣b2可得,
20212﹣2020×2022=20212﹣(2021+1)(2021﹣1)=20212﹣(20212﹣1)
=20212﹣20212+1
=1.
15.解:(1)根据上述操作利用阴影部分的面积关系得到的等式:a2﹣b2=(a+b)(a﹣b),
故答案为:a2﹣b2=(a+b)(a﹣b);
(2)①∵4a2﹣b2=24,
∴(2a+b)(2a﹣b)=24,
∵2a+b=6,
∴2a﹣b=4,
故答案为:4,
②2002﹣1992+1982﹣1972+…+42﹣32+22﹣12
=(200+199)(200﹣199)+(198+197)(198﹣197)+...+(4+3)(4﹣3)+(2+1)(2﹣1)
=200+199+198+197+...+4+3+2+1
=×(200+1)×200
=20100.
三.完全平方公式
16.解:(x﹣3y)(3x+2y)﹣(2x﹣y)2
=3x2+2xy﹣9xy﹣6y2﹣(4x2﹣4xy+y2)
=3x2+2xy﹣9xy﹣6y2﹣4x2+4xy﹣y2
=﹣x2﹣3xy﹣7y2.
17.解:∵(x﹣2)2=x2﹣4x+4,(x﹣2)2=x2+mx+n,
∴x2﹣4x+4=x2+mx+n,
∴m=﹣4,n=4.
故选:B.
18.解:∵(2a﹣m)2=4a2﹣4ma+m2,(2a﹣m)2=4a2+2a+,
∴4a2﹣4ma+m2=4a2+2a+,
∴﹣4m=2,
解得:m=﹣,
故选:D.
19.解:因为(x﹣p)2=x2﹣2px+p2,(x﹣p)2=x2+mx+36,
所以m=﹣2p,p2=36,
所以m=﹣2p,p=±6,
所以m=﹣12或12.
故答案为:﹣12或12.
20.解:根据题意,可得:
(x﹣)2=x2+ax+,
∵(x﹣)2=x2﹣x+,
∴x2﹣x+=x2+ax+,
∴a=﹣1.
故答案为:﹣1.
21.解:由完全平方公式(a+b)2=a2+2ab+b2,
可得a2+b2=(a+b)2﹣2ab,
∴当x+y=﹣5,xy=6时,
x2+y2=(﹣5)2﹣2×6=25﹣12=13,
故答案为:13.
22.解:因为(2a+b)2=(2a﹣b)2+A,(2a+b)2=(2a﹣b)2+8ab,
所以A=8ab.
故答案为:8ab.
23.解:∵a+b=5,(a﹣b)2=13,
∴a2+b2+2ab=25①,a2+b2﹣2ab=13②,
则①﹣②可得:4ab=12,
所以ab=3.
故答案为:3.
24.解:设a﹣2019=x,2020﹣a=y,则x+y=1,
∵(a﹣2019)2+(2020﹣a)2=2021,
∴x2+y2=2021,
∵(x+y)2=x2+2xy+y2,
∴2xy=(x+y)2﹣(x2+y2)=1﹣2021=﹣2020,
即xy=﹣1010,
∴(a﹣2019)(2020﹣a)=xy=﹣1010,
∴(a﹣2019)(a﹣2020)
=﹣(a﹣2019)(2020﹣a)
=﹣xy
=1010.
故答案为:1010.
25.解:根据规律直接写出(a+b)6=a6+6a5b+15a4b2+20a3b3+15a2b3+6ab4+b5,
所以(a+b)6的展开式中字母a、b指数相同的项为20a3b3.
故答案为:20a3b3.
四.完全平方公式的几何背景
26.解:由拼图可得小正方形的边长是小矩形长与宽的差,
即a﹣b,
∴中间小正方形的面积为(a﹣b)2.
故答案应为:(a﹣b)2.
27.解:∵a2+b2=300,ab=12,
∴=
==144.
故答案为:144.
28.解:(1)∵图3面积为(a+2b)(2a+b)=2a2+5ab+2b2,
∴图3可以解释为等式(a+2b)(2a+b)=2a2+5ab+2b2.
(2)需要边长为a的正方形2块,长为b宽为a的长方形3块,边长为b的正方形1块.如下图所示:
整式乘法验证,(a+b)(2a+b)=2a2+ab+2ab+b2=2a2+3ab+b2,
∴需要a×a的正方形2块,需要a×b的长方形3块,需要b×b的正方形1块.
29.解:(1)∵图2中正方形的面积可表示为:(a+b)2和a2+2ab+b2,
∴可得公式(a+b)2=a2+2ab+b2,
故答案为:(a+b)2=a2+2ab+b2;
(2)由计算(2a+b)2=4a2+4ab+b2可得,
需要取甲种纸片4张、乙种纸片4张、丙种纸片1张.
30.解:(1)由题意得,图乙中阴影部分的正方形的边长等于m﹣n;
(2)图乙中阴影部分的面积可表示为:(m+n)2﹣4mn或(m﹣n)2;
(3)由图乙中阴影部分的面积可得等式:(m+n)2﹣4mn=(m﹣n)2;
(4)由(3)题结果(m+n)2﹣4mn=(m﹣n)2可得,
(a﹣b)2=(a+b)2﹣4ab,
∴当a+b=6,ab=3时,
(a﹣b)2=62﹣4×3=36﹣12=24,
即:(a﹣b)2=24.
31.解:(1)由题意得:图2中阴影部分的正方形边长为:a﹣b.
故答案为:a﹣b.
(2)图2中阴影部分面积为:(a﹣b)2,还可以表示为:(a+b)2﹣4ab.
∴(a﹣b)2=(a+b)2﹣4ab.
(3)设AC=x,BC=y,由题意得:x+y=8,x2+y2=S1+S2=34.
∵(x+y)2=x2+y2+2xy.
∴64=34+2xy.
∴xy=15.
∴S阴影=AC CF=xy=7.5.
32.解:(1)由图可得,S1=a2﹣b2,
S2=a2﹣a(a﹣b)﹣b(a﹣b)﹣b(a﹣b)=2b2﹣ab;
(2)S1+S2=a2﹣b2+2b2﹣ab=a2+b2﹣ab,
∵a+b=10,ab=20,
∴S1+S2=a2+b2﹣ab=(a+b)2﹣3ab=100﹣3×20=40;
(3)由图可得,S3=a2+b2﹣b(a+b)﹣a2=(a2+b2﹣ab),
∵S1+S2=a2+b2﹣ab=30,
∴S3=×30=15.
33.解:(1)由完全平方公式(a+b)2=a2+2ab+b2得,ab=,
∴当x+y=8,x2+y2=30时,
xy====17;
(2)①由完全平方公式(a+b)2=a2+2ab+b2得,a2+b2=(a+b)2﹣2ab,
∴当(4﹣x)x=3时,
(4﹣x)2+x2=[(4﹣x)+x]2﹣2(4﹣x)x
=42﹣2×3
=16﹣6
=10,
故答案为:10;
②由完全平方公式(a﹣b)2=a2﹣2ab+b2得,a2+b2=(a﹣b)2+2ab,
∴当(3﹣x)(5﹣x)=6时,
(3﹣x)2+(5﹣x)2=[(3﹣x)﹣(5﹣x)]2+2(3﹣x)(5﹣x)=(﹣2)2+2×6=4+12=16,
故答案为:16;
(3)由完全平方公式(a+b)2=a2+2ab+b2得,=,
∴当AC+BC=AB=10,AC2+BC2=S1+S2=52时,
图中阴影部分面积======12.
五.完全平方式
34.解:∵4x2+kx+25是一个完全平方式,
∴4x2+kx+25=(2x)2+kx+52=(2x±5)2,
∵(2x±5)2=4x2±20x+25,
∴kx=±20x,解得k=±20.
故答案为:±20.
35.解:∵x2﹣(m﹣1)x+49是完全平方式,
∴﹣(m﹣1)=±14,
解得:m=15或﹣13.
故答案为:15或﹣13.
36.解:∵多项式x2+4x﹣m是一个完全平方式,
∴Δ=42﹣4×1×(﹣m)=0,
∴m=﹣4.
故答案为:﹣4.
37.解:∵x2﹣2(a+1)xy+9y2是完全平方式,x2﹣2(a+1)xy+9y2=x2﹣2(a+1)xy+(3y)2,
∴﹣2(a+1)xy=±2×x×3y,
解得a+1=±3,
∴a=2或a=﹣4.
故答案为:2或﹣4.
