5.3平行线的性质 小节培优检测(含答案)2022-2023学年人教版数学七年级下册
文档属性
| 名称 | 5.3平行线的性质 小节培优检测(含答案)2022-2023学年人教版数学七年级下册 | 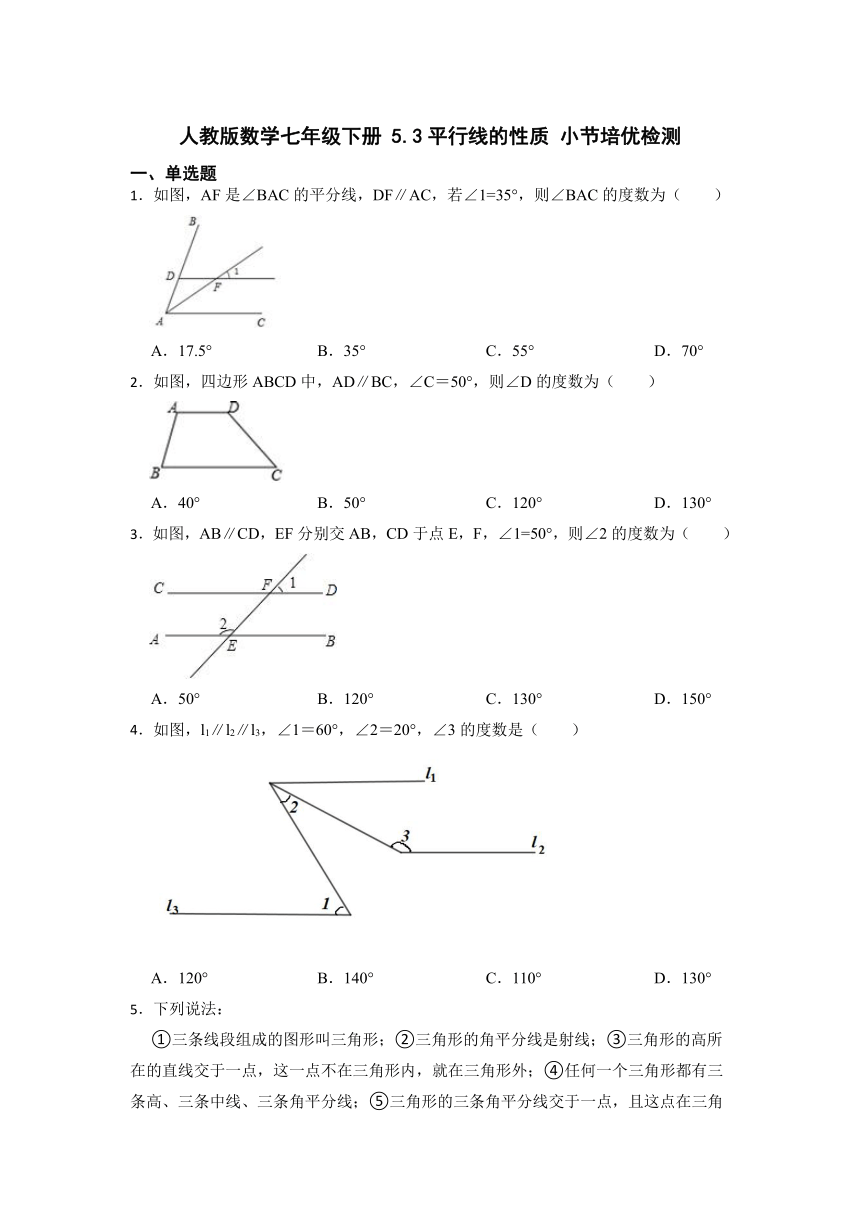 | |
| 格式 | docx | ||
| 文件大小 | 261.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-07 17:53:00 | ||
图片预览



文档简介
人教版数学七年级下册 5.3平行线的性质 小节培优检测
一、单选题
1.如图,AF是∠BAC的平分线,DF∥AC,若∠1=35°,则∠BAC的度数为( )
A.17.5° B.35° C.55° D.70°
2.如图,四边形ABCD中,AD∥BC,∠C=50°,则∠D的度数为( )
A.40° B.50° C.120° D.130°
3.如图,AB∥CD,EF分别交AB,CD于点E,F,∠1=50°,则∠2的度数为( )
A.50° B.120° C.130° D.150°
4.如图,l1∥l2∥l3,∠1=60°,∠2=20°,∠3的度数是( )
A.120° B.140° C.110° D.130°
5.下列说法:
①三条线段组成的图形叫三角形;②三角形的角平分线是射线;③三角形的高所在的直线交于一点,这一点不在三角形内,就在三角形外;④任何一个三角形都有三条高、三条中线、三条角平分线;⑤三角形的三条角平分线交于一点,且这点在三角形内.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
6.如图, ,直线 分别交 , 于点M,N,将一个含有45°角的直角三角尺按如图所示的方式摆放,若 ,则 等于( )
A.15° B.25° C.35° D.45°
7.如图, ,以点B为圆心,小于DB长为半径作圆弧,分别交BA、BD于点E,F,再分别以点E、F为圆心,大于 长为半径作圆弧,两弧交于点G,作射线BG交CD于点H.若 ,则 的大小为( )度.
A.8 B.16 C.32 D.64
8.下列命题中,真命题是( )
A.全等三角形的对应边相等
B.等腰三角形的对称轴是底边上的高
C.两边及其中一边所对的角对应相等的两个三角形全等
D.同位角相等
9.如图,已知a∥b,直角三角板的直角顶点在直线b上,若∠1=60°,则∠2等于( )
A.30° B.40° C.50° D.60°
10.①如图1,AB∥CD,则∠A +∠E +∠C=180°;②如图2,AB∥CD,则∠E =∠A +∠C;③如图3,AB∥CD,则∠A +∠E-∠1=180° ; ④如图4,AB∥CD,则∠A=∠C +∠P.以上结论正确的个数是( )
A.、1个 B.2个 C.3个 D.4个
二、填空题
11.如图,直线a、b被直线c所截,a∥b,∠1=70°,则∠2= .
12.如图,∠AOB的两边OA、OB均为平面反光镜,∠AOB=40°,在射线OB上有一点P,从点P点射出的一束光线经OA上的Q点反射后,反射光线QR恰好与OB平行,则∠QPB的度数是
13.如图,点P是∠NOM的边OM上一点,PD⊥ON于点D,∠OPD=30°,PQ∥ON,则∠MPQ的度数是 .
14.下列四个命题中:
①对顶角相等;②如果两条直线被第三条直线所截,那么同位角相等;③如果两个实数的平方相等,那么这两个实数也相等;④三角形的一个外角等于它的两个内角的和.
其中真命题有 (填序号).
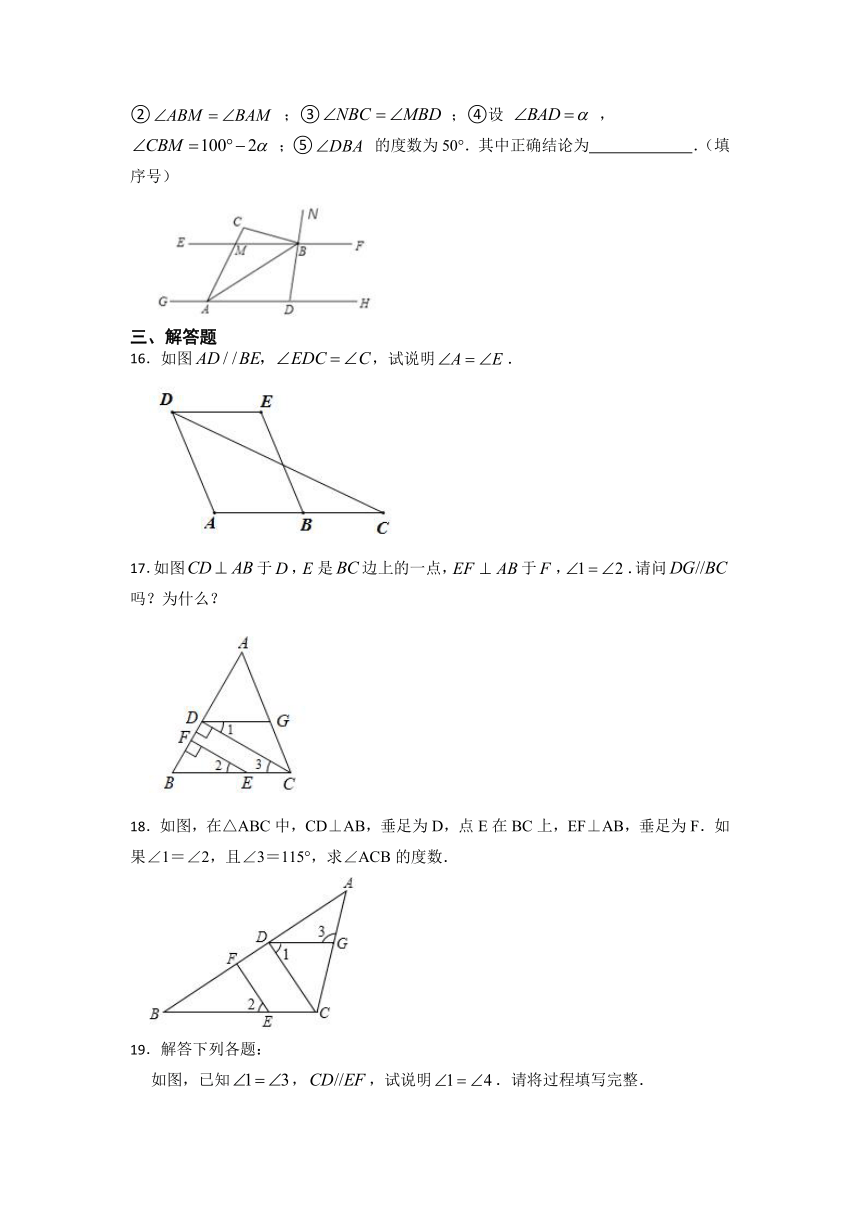
15.如图,已知 , 、 为 上的两点, 、 为 上的两点,延长 于点 , 平分 ,点 在直线 上,且 平分 ,若 .则下列结论:① ;② ;③ ;④设 , ;⑤ 的度数为50°.其中正确结论为 .(填序号)
三、解答题
16.如图,试说明.
17.如图于,是边上的一点,于,.请问吗?为什么?
18.如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.如果∠1=∠2,且∠3=115°,求∠ACB的度数.
19.解答下列各题:
如图,已知,,试说明.请将过程填写完整.
解:∵
又( ▲ )
∴ ▲ .( ▲ )
∴ ▲ ▲ ( ▲ )
又∵
∴ ▲
∴( ▲ )
20.如图,在△ABC中,BD平分∠ABC交AC于点D,DE∥AB交BC于点E,F是BD中点.
求证:EF平分∠BED.
21.如图,点D是∠ABC内部一点,DE∥AB交BC于点E.请你画出射线DF,并且DF∥BC;判断∠B与∠EDF的数量关系,并证明.
22.如图,AB∥CD,分别探讨下面四个图形中∠APC与∠A,∠C的关系,请你从所得的关系中任意选取一个加以说明.
(1)图(1)结论: ;图(2)结论: ;图(3)结论: ;图(4)结论: .
(2)你准备证明的是图 ,请在下面写出证明过程.
答案解析部分
1.【答案】D
2.【答案】D
3.【答案】C
4.【答案】B
5.【答案】B
6.【答案】C
7.【答案】C
8.【答案】A
9.【答案】A
10.【答案】C
11.【答案】110°
12.【答案】80°
13.【答案】60°
14.【答案】①
15.【答案】①②③⑤
16.【答案】证明:∵,
∴,
∴,
∵,
∴,
∴.
17.【答案】解: ;理由如下:
∵,,
∴CD∥EF,
∴,
∵,
∴,
∴.
18.【答案】解:∵CD⊥AB,EF⊥AB,
∴∠CDB=∠EFB=90°,
∴EF//CD;
∴∠2=∠BCD,
∵∠1=∠2,
∴∠1=∠BCD,
∴DG//BC,
∴∠ACB=∠3=115° .
19.【答案】解:∵∠1=∠3
又∠2=∠3 (对顶角相等)
∴∠1=∠2(等量代换)
∴AB∥CD (同位角相等,两直线平行)
又∵CD∥EF
∴AB∥EF
∴(两直线平行,同位角相等).
20.【答案】证明:∵BD平分∠ABC
∴∠ABD=∠CBD
∵DE∥AB
∴∠ABD=∠BDE
∴∠CBD=∠BDE
∵F是BD中点
∴EF平分∠BED.
21.【答案】解:∠B与∠EDF相等或互补. 理由如下: 如图1:∵DE∥AB(已知) ∴∠B=∠DEC(两直线平行,同位角相等) ∵DF∥BC(已知) ∴∠EDF=∠DEC(两直线平行,内错角相等) ∴∠B=∠EDF(等量代换); 如图2, ∵DE∥AB(已知) ∴∠B=∠DEC(两直线平行,同位角相等) ∵DF∥BC(已知) ∴∠EDF+∠DEC=180°(两直线平行,同旁内角互补) ∴∠EDF+∠B=180°(等量代换), 综上所述,∠B与∠EDF相等或互补.
22.【答案】(1)∠APC+∠A+∠C=360°;∠APC=∠A+∠C;∠APC=∠A-∠C;∠APC=∠C-∠A
(2)(1): . 过点P作 , , , , , , ; 图(2): . 过点P作 , , , , , ; 图(3): . 过点P作 , , , , , , ; 图(4): . 过点P作 , , , , , , .
一、单选题
1.如图,AF是∠BAC的平分线,DF∥AC,若∠1=35°,则∠BAC的度数为( )
A.17.5° B.35° C.55° D.70°
2.如图,四边形ABCD中,AD∥BC,∠C=50°,则∠D的度数为( )
A.40° B.50° C.120° D.130°
3.如图,AB∥CD,EF分别交AB,CD于点E,F,∠1=50°,则∠2的度数为( )
A.50° B.120° C.130° D.150°
4.如图,l1∥l2∥l3,∠1=60°,∠2=20°,∠3的度数是( )
A.120° B.140° C.110° D.130°
5.下列说法:
①三条线段组成的图形叫三角形;②三角形的角平分线是射线;③三角形的高所在的直线交于一点,这一点不在三角形内,就在三角形外;④任何一个三角形都有三条高、三条中线、三条角平分线;⑤三角形的三条角平分线交于一点,且这点在三角形内.其中正确的有( )
A.1个 B.2个 C.3个 D.4个
6.如图, ,直线 分别交 , 于点M,N,将一个含有45°角的直角三角尺按如图所示的方式摆放,若 ,则 等于( )
A.15° B.25° C.35° D.45°
7.如图, ,以点B为圆心,小于DB长为半径作圆弧,分别交BA、BD于点E,F,再分别以点E、F为圆心,大于 长为半径作圆弧,两弧交于点G,作射线BG交CD于点H.若 ,则 的大小为( )度.
A.8 B.16 C.32 D.64
8.下列命题中,真命题是( )
A.全等三角形的对应边相等
B.等腰三角形的对称轴是底边上的高
C.两边及其中一边所对的角对应相等的两个三角形全等
D.同位角相等
9.如图,已知a∥b,直角三角板的直角顶点在直线b上,若∠1=60°,则∠2等于( )
A.30° B.40° C.50° D.60°
10.①如图1,AB∥CD,则∠A +∠E +∠C=180°;②如图2,AB∥CD,则∠E =∠A +∠C;③如图3,AB∥CD,则∠A +∠E-∠1=180° ; ④如图4,AB∥CD,则∠A=∠C +∠P.以上结论正确的个数是( )
A.、1个 B.2个 C.3个 D.4个
二、填空题
11.如图,直线a、b被直线c所截,a∥b,∠1=70°,则∠2= .
12.如图,∠AOB的两边OA、OB均为平面反光镜,∠AOB=40°,在射线OB上有一点P,从点P点射出的一束光线经OA上的Q点反射后,反射光线QR恰好与OB平行,则∠QPB的度数是
13.如图,点P是∠NOM的边OM上一点,PD⊥ON于点D,∠OPD=30°,PQ∥ON,则∠MPQ的度数是 .
14.下列四个命题中:
①对顶角相等;②如果两条直线被第三条直线所截,那么同位角相等;③如果两个实数的平方相等,那么这两个实数也相等;④三角形的一个外角等于它的两个内角的和.
其中真命题有 (填序号).
15.如图,已知 , 、 为 上的两点, 、 为 上的两点,延长 于点 , 平分 ,点 在直线 上,且 平分 ,若 .则下列结论:① ;② ;③ ;④设 , ;⑤ 的度数为50°.其中正确结论为 .(填序号)
三、解答题
16.如图,试说明.
17.如图于,是边上的一点,于,.请问吗?为什么?
18.如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.如果∠1=∠2,且∠3=115°,求∠ACB的度数.
19.解答下列各题:
如图,已知,,试说明.请将过程填写完整.
解:∵
又( ▲ )
∴ ▲ .( ▲ )
∴ ▲ ▲ ( ▲ )
又∵
∴ ▲
∴( ▲ )
20.如图,在△ABC中,BD平分∠ABC交AC于点D,DE∥AB交BC于点E,F是BD中点.
求证:EF平分∠BED.
21.如图,点D是∠ABC内部一点,DE∥AB交BC于点E.请你画出射线DF,并且DF∥BC;判断∠B与∠EDF的数量关系,并证明.
22.如图,AB∥CD,分别探讨下面四个图形中∠APC与∠A,∠C的关系,请你从所得的关系中任意选取一个加以说明.
(1)图(1)结论: ;图(2)结论: ;图(3)结论: ;图(4)结论: .
(2)你准备证明的是图 ,请在下面写出证明过程.
答案解析部分
1.【答案】D
2.【答案】D
3.【答案】C
4.【答案】B
5.【答案】B
6.【答案】C
7.【答案】C
8.【答案】A
9.【答案】A
10.【答案】C
11.【答案】110°
12.【答案】80°
13.【答案】60°
14.【答案】①
15.【答案】①②③⑤
16.【答案】证明:∵,
∴,
∴,
∵,
∴,
∴.
17.【答案】解: ;理由如下:
∵,,
∴CD∥EF,
∴,
∵,
∴,
∴.
18.【答案】解:∵CD⊥AB,EF⊥AB,
∴∠CDB=∠EFB=90°,
∴EF//CD;
∴∠2=∠BCD,
∵∠1=∠2,
∴∠1=∠BCD,
∴DG//BC,
∴∠ACB=∠3=115° .
19.【答案】解:∵∠1=∠3
又∠2=∠3 (对顶角相等)
∴∠1=∠2(等量代换)
∴AB∥CD (同位角相等,两直线平行)
又∵CD∥EF
∴AB∥EF
∴(两直线平行,同位角相等).
20.【答案】证明:∵BD平分∠ABC
∴∠ABD=∠CBD
∵DE∥AB
∴∠ABD=∠BDE
∴∠CBD=∠BDE
∵F是BD中点
∴EF平分∠BED.
21.【答案】解:∠B与∠EDF相等或互补. 理由如下: 如图1:∵DE∥AB(已知) ∴∠B=∠DEC(两直线平行,同位角相等) ∵DF∥BC(已知) ∴∠EDF=∠DEC(两直线平行,内错角相等) ∴∠B=∠EDF(等量代换); 如图2, ∵DE∥AB(已知) ∴∠B=∠DEC(两直线平行,同位角相等) ∵DF∥BC(已知) ∴∠EDF+∠DEC=180°(两直线平行,同旁内角互补) ∴∠EDF+∠B=180°(等量代换), 综上所述,∠B与∠EDF相等或互补.
22.【答案】(1)∠APC+∠A+∠C=360°;∠APC=∠A+∠C;∠APC=∠A-∠C;∠APC=∠C-∠A
(2)(1): . 过点P作 , , , , , , ; 图(2): . 过点P作 , , , , , ; 图(3): . 过点P作 , , , , , , ; 图(4): . 过点P作 , , , , , , .
