2022-2023学年人教版八年级数学下册18.2.3正方形 同步练习(二)(含答案)
文档属性
| 名称 | 2022-2023学年人教版八年级数学下册18.2.3正方形 同步练习(二)(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 725.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-07 19:32:01 | ||
图片预览

文档简介
18.2.3正方形 同步练习(二)
一、单选题
1.下列说法不正确的是( )
A.对角线互相垂直平分的四边形是正方形
B.菱形的对角线互相垂直
C.矩形的对角线相等
D.对角线互相平分的四边形是平行四边形
2.如图,点O为矩形的对称中心,点E从点A出发沿向点B运动,移动到点B停止,延长EO交于点F,则四边形形状的变化依次为( )
A.矩形→菱形→平行四边形→矩形 B.平行四边形→菱形→平行四边形→矩形
C.平行四边形→正方形→菱形→矩形 D.平行四边形→菱形→正方形→矩形
3.如图,点E是正方形对角线上一点,过E作交于F,连接,若,,则的长为( )
A. B. C. D.
4.如图:是边长为1的正方形的对角线上一点,且,为上任意一点,于点,于点,则的值是( )
A. B. C. D.
5.在数学拓展课上,小明发现:若一条直线经过平行四边形对角线的交点,则这条直线平分该平行四边形的面积.如图是由5个边长为的小正方形拼成的图形,是其中4个小正方形的公共顶点,小强在小明的启发下,将该图形沿着过点的某条直线剪一刀,把它剪成了面积相等的两部分,则剪痕的长度是( )
A. B. C. D.
6.如图所示,顺次连接四边形各边中点得到四边形,使四边形为正方形,应添加的条件分别是( )
A.且 B.且
C.且 D.且
7.如图,矩形纸片中,,现将其沿对折,使得点落在边上的点处,折痕与边交于点,则的长为( )
A. B. C. D.
8.如图,正方形ABCO和正方形DEFO的顶点A,O,E在同一直线l上,且EF=,AB=3,给出下列结论:
①∠COD=45°;
②AE=5;
③CF=AD;
④△COF的面积是3.
其中正确的结论为( )
A.①② B.①④ C.①②③ D.①③④
9.如图,在四边形中,,,,.为上一点,且.若,则的长为( )
A. B. C.1 D.
10.如图,已知四边形为正方形,,为对角线上一点,连接,过点作,交的延长线于点,以,为邻边作矩形,连接.下列结论:①矩形是正方形;②;③平分;④.其中结论正确的序号有( )
A.①③ B.②④ C.①②③ D.①②③④
二、填空题
11.如图,正方形中,,动点从点出发向点运动,同时动点从点出发向点运动,点、运动的速度相同,当它们到达各自终点时停止运动,运动过程中线段、相交于点,是线段上任意一点,则的最小值为___.
12.如图,四边形中,对角线,且,,各边中点分别为,,,,顺次连接得到四边形;再取各边中点,,,,顺次连接得到四边形;依此类推,这样得到四边形,则四边形的面积为____.
13.如图,点E是正方形ABCD的边CD上一点,以BE为边向上作平行四边形BEFG,连接AG、AF、BF,若,的面积是2,则的面积是_________.
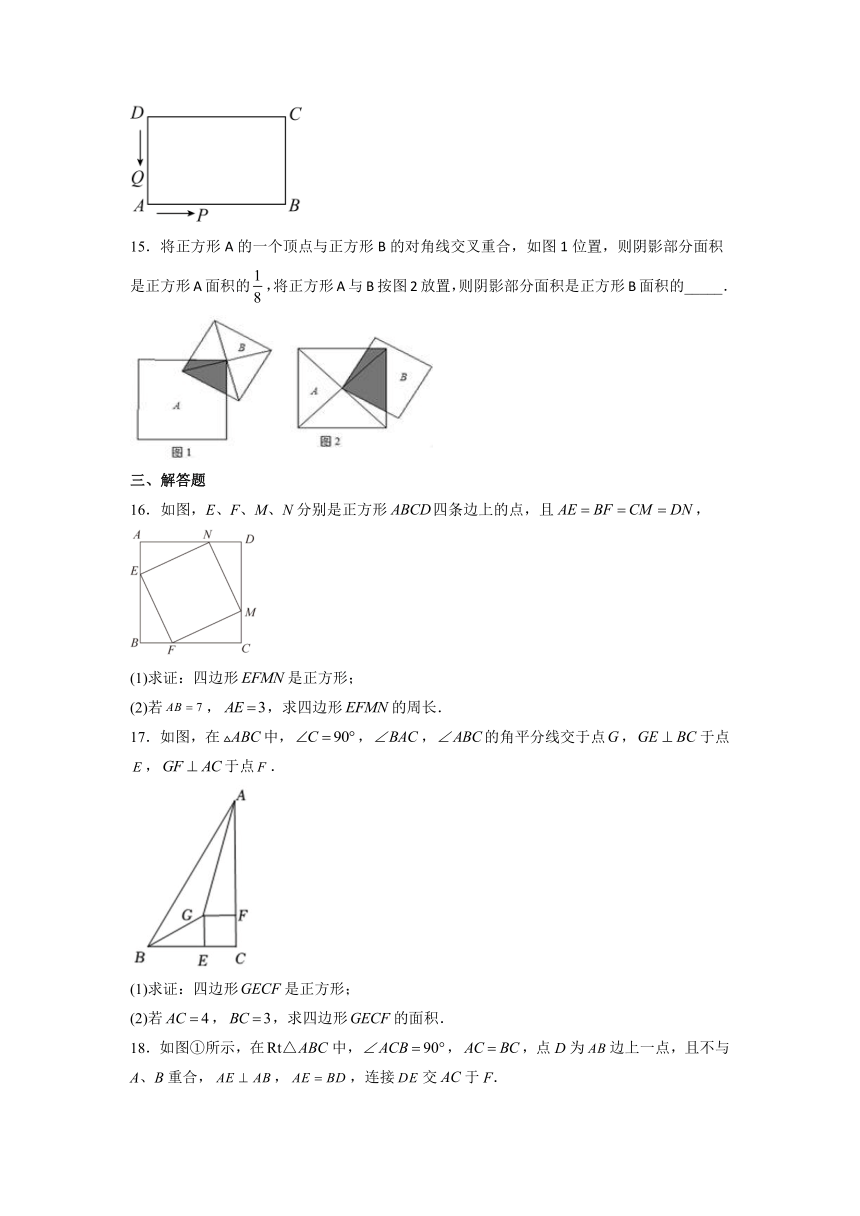
14.如图,长方形中,,,点从出发,以的速度沿运动,最终到达点,在点运动了3秒后点开始以的速度从运动到,在运动过程中,设点的运动时间为,则当的面积为时,的值为________.
15.将正方形A的一个顶点与正方形B的对角线交叉重合,如图1位置,则阴影部分面积是正方形A面积的,将正方形A与B按图2放置,则阴影部分面积是正方形B面积的_____.
三、解答题
16.如图,E、F、M、N分别是正方形四条边上的点,且,
(1)求证:四边形是正方形;
(2)若,,求四边形的周长.
17.如图,在中,,,的角平分线交于点,于点,于点.
(1)求证:四边形是正方形;
(2)若,,求四边形的面积.
18.如图①所示,在中,,,点D为边上一点,且不与A、B重合,,,连接交于F.
(1)求证:;
(2)判断的形状并证明你的结论;
(3)若,点D在边上的什么位置时,能使成为直角三角形?请你在备用图②中画出相应的图形,并直接写出此时线段的长.
19.已知:四边形ABCD是正方形,,点E,F,G,H分别在边AB,BC,AD,DC上.
(1)如图1,若,,则的度数为________;
(2)如图2,若,点E,F分别是AB,BC上的动点,求的周长;
(3)如图3,若,GF和EH交于点O,且,求EH的长度。
参考答案
1--10ABDCA DBCCA
11.
12.(或或,只要答案正确即可)
13.11.
14.2或
15.
16.(1)证明:∵,
∴,
∵,
∴,
∴,,
∴四边形是菱形,
∵,
∴,
∴,
∴四边形是正方形;
(2)解:∵,,
∴,
∴,
∴正方形EFMN的周长为:.
17.(1)证明:过作于,
、的角平分线交于点,于点,于点,
,,
,
是直角三角形,,,,
,
四边形是矩形,
,
四边形为正方形;
(2)
解:如图,连接,过作于,
由勾股定理得:,
设,则,
,
,
,
四边形的面积.
18.(1)证明:∵,,
∴.
∵,
∴.
∴.
∴.
在和D中,
,
∴
(2)解:是等腰直角三角形,理由如下:
∵,
∴,.
∵,
∴.
即.
∴,
∴是等腰直角三角形;
(3)解:点D在边的中点位置时,能使成为直角三角形,如图②,
∵点D是的中点,,
∴,,
∵是等腰直角三角形,
∴四边形是正方形,
∴,
∴为直角三角形,
∵,
∴线段的长为1.
19.(1)解:如图1,∵四边形ABCD是正方形,
∴AD=CD,∠A=∠C=∠ADC=90°,
∵AE=CF,
∴△ADE≌△CDF(SAS),
∴∠ADE=∠CDF,
∵∠EDF=45°,
∴∠ADE+∠CDF=90-45°=45°,
∴∠CDF+∠CDF=45°,
∴∠CDF=22.5°,
∴∠DFC=90°-22.5°=67.5°.
(2)如图2,延长BC到点K,使,连接DK,
∵,
∴,
∴,
∴,,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
即的周长为40;
(3)如图3,作,交AB于点L,交FG于点P,作,交BC于点M,交EH于点Q,连接LM,
∵,,
∴四边形DLEH、四边形DGFM、四边形OPDQ都是平行四边形,
∴,,,
∴;
由(2)得,,
∴,
∴,
∵,
∴,
∴,
解得,
∴,
∵,
∴,
∴.
一、单选题
1.下列说法不正确的是( )
A.对角线互相垂直平分的四边形是正方形
B.菱形的对角线互相垂直
C.矩形的对角线相等
D.对角线互相平分的四边形是平行四边形
2.如图,点O为矩形的对称中心,点E从点A出发沿向点B运动,移动到点B停止,延长EO交于点F,则四边形形状的变化依次为( )
A.矩形→菱形→平行四边形→矩形 B.平行四边形→菱形→平行四边形→矩形
C.平行四边形→正方形→菱形→矩形 D.平行四边形→菱形→正方形→矩形
3.如图,点E是正方形对角线上一点,过E作交于F,连接,若,,则的长为( )
A. B. C. D.
4.如图:是边长为1的正方形的对角线上一点,且,为上任意一点,于点,于点,则的值是( )
A. B. C. D.
5.在数学拓展课上,小明发现:若一条直线经过平行四边形对角线的交点,则这条直线平分该平行四边形的面积.如图是由5个边长为的小正方形拼成的图形,是其中4个小正方形的公共顶点,小强在小明的启发下,将该图形沿着过点的某条直线剪一刀,把它剪成了面积相等的两部分,则剪痕的长度是( )
A. B. C. D.
6.如图所示,顺次连接四边形各边中点得到四边形,使四边形为正方形,应添加的条件分别是( )
A.且 B.且
C.且 D.且
7.如图,矩形纸片中,,现将其沿对折,使得点落在边上的点处,折痕与边交于点,则的长为( )
A. B. C. D.
8.如图,正方形ABCO和正方形DEFO的顶点A,O,E在同一直线l上,且EF=,AB=3,给出下列结论:
①∠COD=45°;
②AE=5;
③CF=AD;
④△COF的面积是3.
其中正确的结论为( )
A.①② B.①④ C.①②③ D.①③④
9.如图,在四边形中,,,,.为上一点,且.若,则的长为( )
A. B. C.1 D.
10.如图,已知四边形为正方形,,为对角线上一点,连接,过点作,交的延长线于点,以,为邻边作矩形,连接.下列结论:①矩形是正方形;②;③平分;④.其中结论正确的序号有( )
A.①③ B.②④ C.①②③ D.①②③④
二、填空题
11.如图,正方形中,,动点从点出发向点运动,同时动点从点出发向点运动,点、运动的速度相同,当它们到达各自终点时停止运动,运动过程中线段、相交于点,是线段上任意一点,则的最小值为___.
12.如图,四边形中,对角线,且,,各边中点分别为,,,,顺次连接得到四边形;再取各边中点,,,,顺次连接得到四边形;依此类推,这样得到四边形,则四边形的面积为____.
13.如图,点E是正方形ABCD的边CD上一点,以BE为边向上作平行四边形BEFG,连接AG、AF、BF,若,的面积是2,则的面积是_________.
14.如图,长方形中,,,点从出发,以的速度沿运动,最终到达点,在点运动了3秒后点开始以的速度从运动到,在运动过程中,设点的运动时间为,则当的面积为时,的值为________.
15.将正方形A的一个顶点与正方形B的对角线交叉重合,如图1位置,则阴影部分面积是正方形A面积的,将正方形A与B按图2放置,则阴影部分面积是正方形B面积的_____.
三、解答题
16.如图,E、F、M、N分别是正方形四条边上的点,且,
(1)求证:四边形是正方形;
(2)若,,求四边形的周长.
17.如图,在中,,,的角平分线交于点,于点,于点.
(1)求证:四边形是正方形;
(2)若,,求四边形的面积.
18.如图①所示,在中,,,点D为边上一点,且不与A、B重合,,,连接交于F.
(1)求证:;
(2)判断的形状并证明你的结论;
(3)若,点D在边上的什么位置时,能使成为直角三角形?请你在备用图②中画出相应的图形,并直接写出此时线段的长.
19.已知:四边形ABCD是正方形,,点E,F,G,H分别在边AB,BC,AD,DC上.
(1)如图1,若,,则的度数为________;
(2)如图2,若,点E,F分别是AB,BC上的动点,求的周长;
(3)如图3,若,GF和EH交于点O,且,求EH的长度。
参考答案
1--10ABDCA DBCCA
11.
12.(或或,只要答案正确即可)
13.11.
14.2或
15.
16.(1)证明:∵,
∴,
∵,
∴,
∴,,
∴四边形是菱形,
∵,
∴,
∴,
∴四边形是正方形;
(2)解:∵,,
∴,
∴,
∴正方形EFMN的周长为:.
17.(1)证明:过作于,
、的角平分线交于点,于点,于点,
,,
,
是直角三角形,,,,
,
四边形是矩形,
,
四边形为正方形;
(2)
解:如图,连接,过作于,
由勾股定理得:,
设,则,
,
,
,
四边形的面积.
18.(1)证明:∵,,
∴.
∵,
∴.
∴.
∴.
在和D中,
,
∴
(2)解:是等腰直角三角形,理由如下:
∵,
∴,.
∵,
∴.
即.
∴,
∴是等腰直角三角形;
(3)解:点D在边的中点位置时,能使成为直角三角形,如图②,
∵点D是的中点,,
∴,,
∵是等腰直角三角形,
∴四边形是正方形,
∴,
∴为直角三角形,
∵,
∴线段的长为1.
19.(1)解:如图1,∵四边形ABCD是正方形,
∴AD=CD,∠A=∠C=∠ADC=90°,
∵AE=CF,
∴△ADE≌△CDF(SAS),
∴∠ADE=∠CDF,
∵∠EDF=45°,
∴∠ADE+∠CDF=90-45°=45°,
∴∠CDF+∠CDF=45°,
∴∠CDF=22.5°,
∴∠DFC=90°-22.5°=67.5°.
(2)如图2,延长BC到点K,使,连接DK,
∵,
∴,
∴,
∴,,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
∴,
∵,
∴,
即的周长为40;
(3)如图3,作,交AB于点L,交FG于点P,作,交BC于点M,交EH于点Q,连接LM,
∵,,
∴四边形DLEH、四边形DGFM、四边形OPDQ都是平行四边形,
∴,,,
∴;
由(2)得,,
∴,
∴,
∵,
∴,
∴,
解得,
∴,
∵,
∴,
∴.
