2022-2023学年北师大版八年级数学下册第一章三角形的证明单元测试题(无答案)
文档属性
| 名称 | 2022-2023学年北师大版八年级数学下册第一章三角形的证明单元测试题(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 162.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-07 18:13:26 | ||
图片预览


文档简介
第一章 三角形的证明 单元测试题 2022-2023学年北师大版八年级数学下册
一、选择题(本大题有10小题,每小题3分,共30分)
1.到三角形的三个顶点距离相等的点是( )
A.三角形三个内角平分线的交点 B.三角形三条中线的交点
C.三角形三条高(所在直线)的交点 D.三角形三条边的垂直平分线的交点
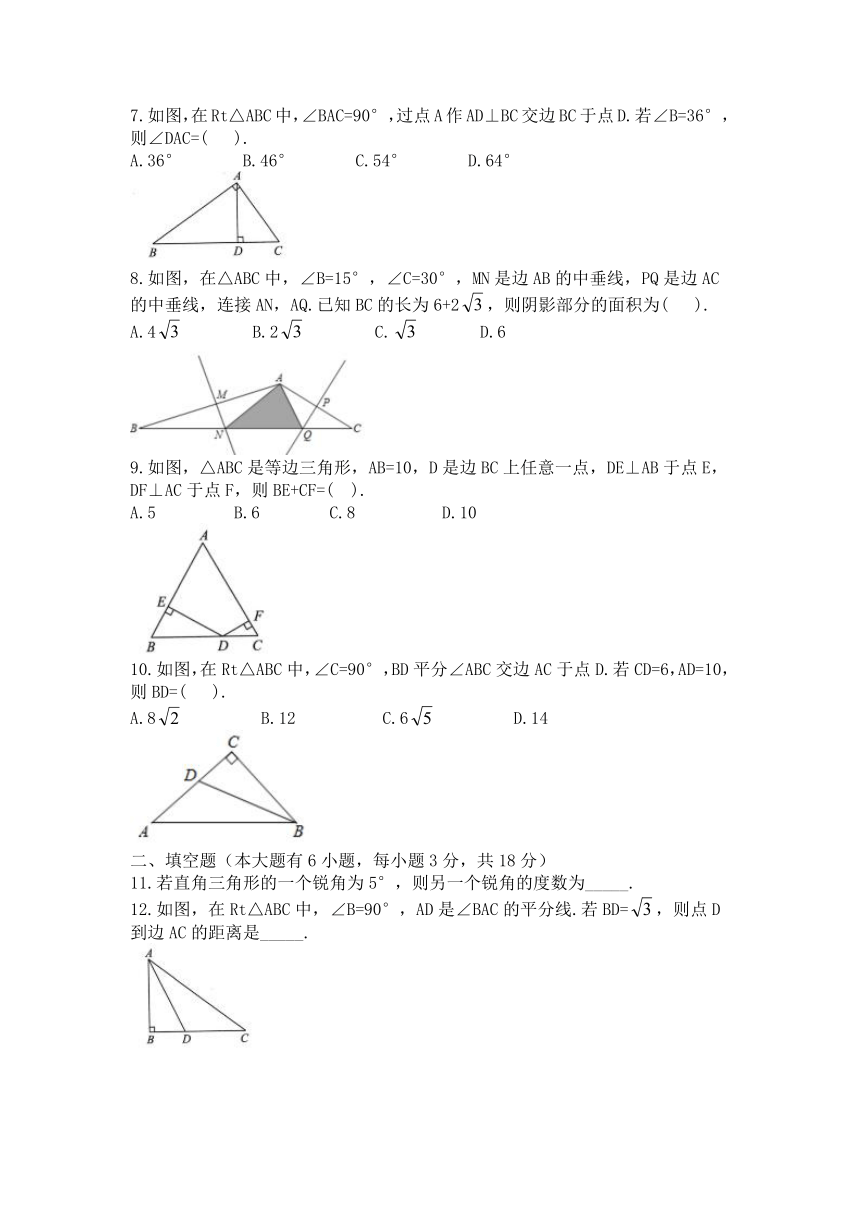
2.如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=6,则AB=( ).
A.10 B.12 C.15 D.30
3.若实数m,n满足等式m-2+=0,且m,n恰好是等腰△ABC的两条边的边长,则△ABC的周长是( ).
A.12 B.10 C.8 D.6
4.如图,已知直线11,l2,l3两两相交,且11⊥3.若α=50°,则β=( ).
A.120° B.130° C.140° D.150°
5.如图,在等腰△ABC中,点D,E分别在腰AB,AC上,添加下列条件,不能判定△ABE≌△ACD的是( ).
A.AD=AE B.BE=CD C.∠ADC=∠AEB D.∠DCB=∠EBC
6.如图,在△ABC中,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB.若AB=4,CF=3,则BD的长是( ).
A.0.5 B.1 C.1.5 D.2
7.如图,在Rt△ABC中,∠BAC=90°,过点A作AD⊥BC交边BC于点D.若∠B=36°,则∠DAC=( ).
A.36° B.46° C.54° D.64°
8.如图,在△ABC中,∠B=15°,∠C=30°,MN是边AB的中垂线,PQ是边AC的中垂线,连接AN,AQ.已知BC的长为6+2,则阴影部分的面积为( ).
A.4 B.2 C. D.6
9.如图,△ABC是等边三角形,AB=10,D是边BC上任意一点,DE⊥AB于点E,DF⊥AC于点F,则BE+CF=( ).
A.5 B.6 C.8 D.10
10.如图,在Rt△ABC中,∠C=90°,BD平分∠ABC交边AC于点D.若CD=6,AD=10,则BD=( ).
A.8 B.12 C.6 D.14
二、填空题(本大题有6小题,每小题3分,共18分)
11.若直角三角形的一个锐角为5°,则另一个锐角的度数为_____.
12.如图,在Rt△ABC中,∠B=90°,AD是∠BAC的平分线.若BD=,则点D到边AC的距离是_____.
13.如图,在△ABC中,AB=AC,过点A作AD⊥AB,交边BC于点D,∠ADB=70°,则∠CAD=_____.
14.如图,在Rt△ABC中,∠ACB=90°,CD为斜边AB上的中线.若CD=3,则AB=_____.
15.如图,在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=10,BD=17,BC=15,则四边形ABCD的面积为_____.
16.在△ABC中,∠ABC=60°,AD是边BC上的高,AD=4,CD=1,则△ABC的面积为_____.
三、解答题(本大题有8小题,共52分)
17.(6分)如图,在△ABC中,AB=AC,∠BAC=120°,AB的垂直平分线交边BC于点D,连接AD
(1)求∠ADC的度数;
(2)求证:DC=2DB.
18.(6分)如图,在Rt△ABC中,∠C=90°,AD平分∠CAB交边BC于点D,DE⊥AB于点E,点F在边AC上,且BE=FC.求证:BD=DF.
19.(6分)如图,在△ABC中,∠BAC=100°,∠C=50°,AD⊥BC,垂足为D,EF是边AB的垂直平分线,交边BC于点E,交边AB于点F,连接AE,求∠EAD的度数.
20.(6分)如图,在△ABC中,AD是边BC上的高,CE是边AB上的中线,G是CE的中点,DG⊥CE,垂足为G.
(1)求证:DC=BE;
(2)若∠AEC=66°,求∠BCE的度数.
21.(6分)如图,O为△ABC的两条角平分线的交点,过点O作OD⊥BC于点D,且OD=2cm.若△ABC的周长是31cm,求△ABC的面积.
22.(6分)如图,在等腰△ADC中,AD=CD,AB∥CD,CB⊥AB,CE⊥AD交AD的延长线于点E.
(1)求证:CE=CB;
(2)连接BE,请你判断BE与AC的位置关系,并说明理由.
23.(8分)如图,D为等腰Rt△ABC内一点,∠ACB=90°,∠CAD=∠CBD=15°,E为AD延长线上一点,且CE=CA.
(1)求证:DE平分∠BDC;
(2)若点M在DE上,且CD=DM,求证:ME=BD.
24.(8分)在△ABC中,AB=AC.
(1)如图①,若∠BAD=30°,AD是边BC上的高,AD=AE,则∠EDC=_____.
(2)如图②,若∠BAD=40°,AD是边BC上的高,AD=AE,则∠EDC=_____.
(3)思考:通过以上两题,你发现∠BAD与∠EDC之间有什么关系?请用式子表示:____________.
(4)如图③,若AD不是边BC上的高,AD=AE,则是否仍有上述关系?如有,请你写出来,并说明理由.
一、选择题(本大题有10小题,每小题3分,共30分)
1.到三角形的三个顶点距离相等的点是( )
A.三角形三个内角平分线的交点 B.三角形三条中线的交点
C.三角形三条高(所在直线)的交点 D.三角形三条边的垂直平分线的交点
2.如图,在Rt△ABC中,∠C=90°,∠A=30°,BC=6,则AB=( ).
A.10 B.12 C.15 D.30
3.若实数m,n满足等式m-2+=0,且m,n恰好是等腰△ABC的两条边的边长,则△ABC的周长是( ).
A.12 B.10 C.8 D.6
4.如图,已知直线11,l2,l3两两相交,且11⊥3.若α=50°,则β=( ).
A.120° B.130° C.140° D.150°
5.如图,在等腰△ABC中,点D,E分别在腰AB,AC上,添加下列条件,不能判定△ABE≌△ACD的是( ).
A.AD=AE B.BE=CD C.∠ADC=∠AEB D.∠DCB=∠EBC
6.如图,在△ABC中,D是AB上一点,DF交AC于点E,DE=FE,FC∥AB.若AB=4,CF=3,则BD的长是( ).
A.0.5 B.1 C.1.5 D.2
7.如图,在Rt△ABC中,∠BAC=90°,过点A作AD⊥BC交边BC于点D.若∠B=36°,则∠DAC=( ).
A.36° B.46° C.54° D.64°
8.如图,在△ABC中,∠B=15°,∠C=30°,MN是边AB的中垂线,PQ是边AC的中垂线,连接AN,AQ.已知BC的长为6+2,则阴影部分的面积为( ).
A.4 B.2 C. D.6
9.如图,△ABC是等边三角形,AB=10,D是边BC上任意一点,DE⊥AB于点E,DF⊥AC于点F,则BE+CF=( ).
A.5 B.6 C.8 D.10
10.如图,在Rt△ABC中,∠C=90°,BD平分∠ABC交边AC于点D.若CD=6,AD=10,则BD=( ).
A.8 B.12 C.6 D.14
二、填空题(本大题有6小题,每小题3分,共18分)
11.若直角三角形的一个锐角为5°,则另一个锐角的度数为_____.
12.如图,在Rt△ABC中,∠B=90°,AD是∠BAC的平分线.若BD=,则点D到边AC的距离是_____.
13.如图,在△ABC中,AB=AC,过点A作AD⊥AB,交边BC于点D,∠ADB=70°,则∠CAD=_____.
14.如图,在Rt△ABC中,∠ACB=90°,CD为斜边AB上的中线.若CD=3,则AB=_____.
15.如图,在四边形ABCD中,∠BCD=90°,BD平分∠ABC,AB=10,BD=17,BC=15,则四边形ABCD的面积为_____.
16.在△ABC中,∠ABC=60°,AD是边BC上的高,AD=4,CD=1,则△ABC的面积为_____.
三、解答题(本大题有8小题,共52分)
17.(6分)如图,在△ABC中,AB=AC,∠BAC=120°,AB的垂直平分线交边BC于点D,连接AD
(1)求∠ADC的度数;
(2)求证:DC=2DB.
18.(6分)如图,在Rt△ABC中,∠C=90°,AD平分∠CAB交边BC于点D,DE⊥AB于点E,点F在边AC上,且BE=FC.求证:BD=DF.
19.(6分)如图,在△ABC中,∠BAC=100°,∠C=50°,AD⊥BC,垂足为D,EF是边AB的垂直平分线,交边BC于点E,交边AB于点F,连接AE,求∠EAD的度数.
20.(6分)如图,在△ABC中,AD是边BC上的高,CE是边AB上的中线,G是CE的中点,DG⊥CE,垂足为G.
(1)求证:DC=BE;
(2)若∠AEC=66°,求∠BCE的度数.
21.(6分)如图,O为△ABC的两条角平分线的交点,过点O作OD⊥BC于点D,且OD=2cm.若△ABC的周长是31cm,求△ABC的面积.
22.(6分)如图,在等腰△ADC中,AD=CD,AB∥CD,CB⊥AB,CE⊥AD交AD的延长线于点E.
(1)求证:CE=CB;
(2)连接BE,请你判断BE与AC的位置关系,并说明理由.
23.(8分)如图,D为等腰Rt△ABC内一点,∠ACB=90°,∠CAD=∠CBD=15°,E为AD延长线上一点,且CE=CA.
(1)求证:DE平分∠BDC;
(2)若点M在DE上,且CD=DM,求证:ME=BD.
24.(8分)在△ABC中,AB=AC.
(1)如图①,若∠BAD=30°,AD是边BC上的高,AD=AE,则∠EDC=_____.
(2)如图②,若∠BAD=40°,AD是边BC上的高,AD=AE,则∠EDC=_____.
(3)思考:通过以上两题,你发现∠BAD与∠EDC之间有什么关系?请用式子表示:____________.
(4)如图③,若AD不是边BC上的高,AD=AE,则是否仍有上述关系?如有,请你写出来,并说明理由.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
