2022-2023学年人教版八年级数学下册16.1二次根式同步练习(无答案)
文档属性
| 名称 | 2022-2023学年人教版八年级数学下册16.1二次根式同步练习(无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 279.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-07 00:00:00 | ||
图片预览
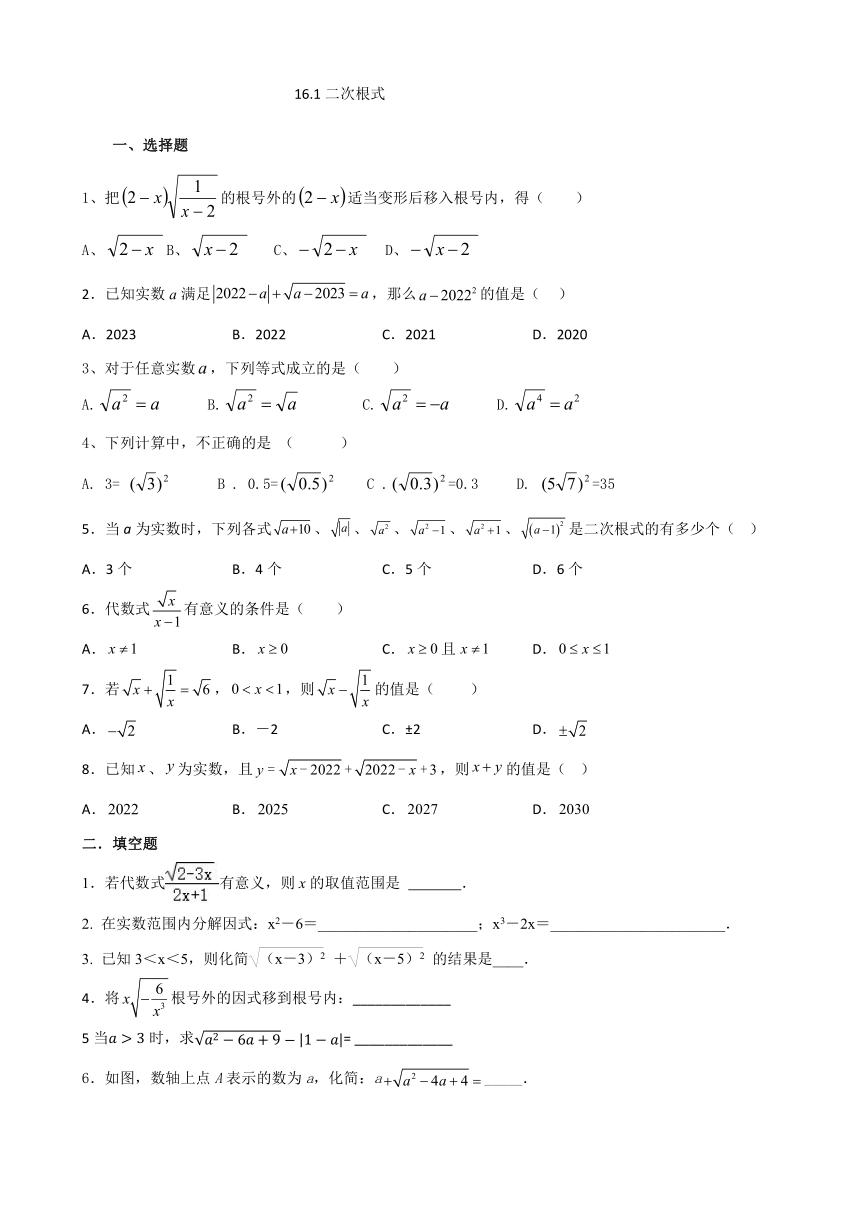

文档简介
16.1二次根式
选择题
1、把的根号外的适当变形后移入根号内,得( )
A、B、 C、 D、
2.已知实数a满足,那么的值是( )
A.2023 B.2022 C.2021 D.2020
3、对于任意实数,下列等式成立的是( )
A. B. C. D.
4、下列计算中,不正确的是 ( )
A. 3= B . 0.5= C .=0.3 D. =35
5.当a为实数时,下列各式、、、、、是二次根式的有多少个( )
A.3个 B.4个 C.5个 D.6个
6.代数式有意义的条件是( )
A. B. C.且 D.
7.若,,则的值是( )
A. B.-2 C.±2 D.
8.已知、为实数,且,则的值是( )
A. B. C. D.
填空题
1.若代数式有意义,则x的取值范围是 .
2. 在实数范围内分解因式:x2-6=_____________________;x3-2x=_______________________.
3. 已知3<x<5,则化简+的结果是____.
4.将根号外的因式移到根号内:_____________
5当时,求= _____________
6.如图,数轴上点A表示的数为a,化简:a_____.
解答题
1、计算 1).()2(x≥0) 2).()2
2.计算:
(1).
(2).
3.当时,求的值.如图是小亮和小芳的解答过程:
(1) 的解法是错误的;
(2)错误的原因在于未能正确地运用二次根式的性质: ;
(3)当时,求的值.
4.小颖利用平方差公式,自己探究出一种解某一类根式方程的方法.下面是她解方程+=5的过程.
解:设﹣=m,与原方程相乘得:
(+)×()=5m,
x﹣2﹣(x﹣7)=5m,解之得m=1,
∴﹣=1,与原方程相加得:
(+)+()=5+1,
2=6,解之得,x=11,经检验,x=11是原方程的根.
学习借鉴解法,解方程﹣=1.
5.求代数式a+,a=1007,如图是小亮和小芳的解答过程:
(1) 的解法是正确的;
(2)化简代数式a+,(其中a<0);
(3)若=13,直接写出a的取值范围.
6 先阅读下面的解题过程,然后再解答,形如的化简,我们只要找到两个数a,b,使,,即,,那么便有:.
例如化简:
解:首先把化为,
这里,,
由于,,
所以,
所以
(1)根据上述方法化简:
(2)根据上述方法化简:
(3)根据上述方法化简:
选择题
1、把的根号外的适当变形后移入根号内,得( )
A、B、 C、 D、
2.已知实数a满足,那么的值是( )
A.2023 B.2022 C.2021 D.2020
3、对于任意实数,下列等式成立的是( )
A. B. C. D.
4、下列计算中,不正确的是 ( )
A. 3= B . 0.5= C .=0.3 D. =35
5.当a为实数时,下列各式、、、、、是二次根式的有多少个( )
A.3个 B.4个 C.5个 D.6个
6.代数式有意义的条件是( )
A. B. C.且 D.
7.若,,则的值是( )
A. B.-2 C.±2 D.
8.已知、为实数,且,则的值是( )
A. B. C. D.
填空题
1.若代数式有意义,则x的取值范围是 .
2. 在实数范围内分解因式:x2-6=_____________________;x3-2x=_______________________.
3. 已知3<x<5,则化简+的结果是____.
4.将根号外的因式移到根号内:_____________
5当时,求= _____________
6.如图,数轴上点A表示的数为a,化简:a_____.
解答题
1、计算 1).()2(x≥0) 2).()2
2.计算:
(1).
(2).
3.当时,求的值.如图是小亮和小芳的解答过程:
(1) 的解法是错误的;
(2)错误的原因在于未能正确地运用二次根式的性质: ;
(3)当时,求的值.
4.小颖利用平方差公式,自己探究出一种解某一类根式方程的方法.下面是她解方程+=5的过程.
解:设﹣=m,与原方程相乘得:
(+)×()=5m,
x﹣2﹣(x﹣7)=5m,解之得m=1,
∴﹣=1,与原方程相加得:
(+)+()=5+1,
2=6,解之得,x=11,经检验,x=11是原方程的根.
学习借鉴解法,解方程﹣=1.
5.求代数式a+,a=1007,如图是小亮和小芳的解答过程:
(1) 的解法是正确的;
(2)化简代数式a+,(其中a<0);
(3)若=13,直接写出a的取值范围.
6 先阅读下面的解题过程,然后再解答,形如的化简,我们只要找到两个数a,b,使,,即,,那么便有:.
例如化简:
解:首先把化为,
这里,,
由于,,
所以,
所以
(1)根据上述方法化简:
(2)根据上述方法化简:
(3)根据上述方法化简:
