圆柱的表面积(课件)人教版六年级下册数学 (共16张PPT)
文档属性
| 名称 | 圆柱的表面积(课件)人教版六年级下册数学 (共16张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 676.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-07 00:00:00 | ||
图片预览



文档简介
(共16张PPT)
圆柱的表面积
课前热身
1、圆柱有( )个底面,它们是( );
有( )侧面,是( ),有( )条高,
这些高都( )。
2、圆柱的侧面展开是( ),
长方形的长等于( ),宽是( )。
3、圆的面积公式=
4、圆的周长公式=
5、长方形的面积公式=
2
大小一样的圆
1
曲面
无数
长度相等
长方形或正方形
底面周长
圆柱的高
S=πr2
C=2πr
或C=πd
长×宽
做一个茶叶筒需要多大面积纸板
探究新知
说一说该求哪部分的面积。
茶叶
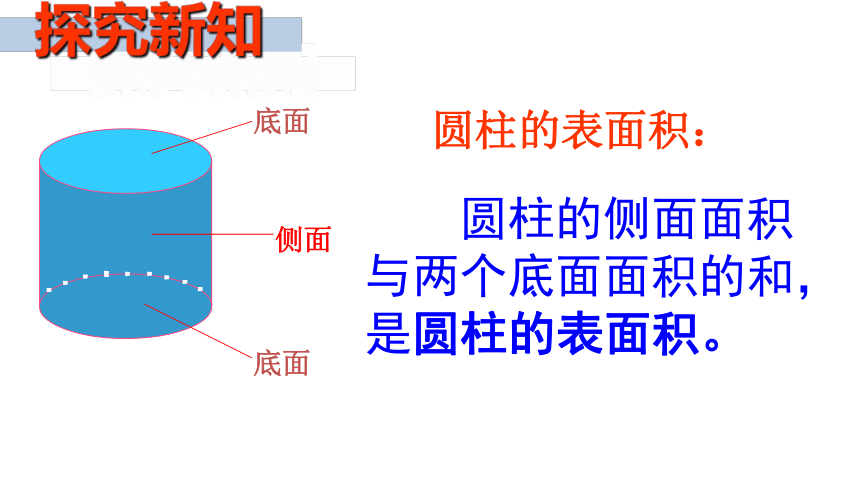
底面
底面
侧面
圆柱的侧面面积与两个底面面积的和,是圆柱的表面积。
圆柱的表面积:
探究新知
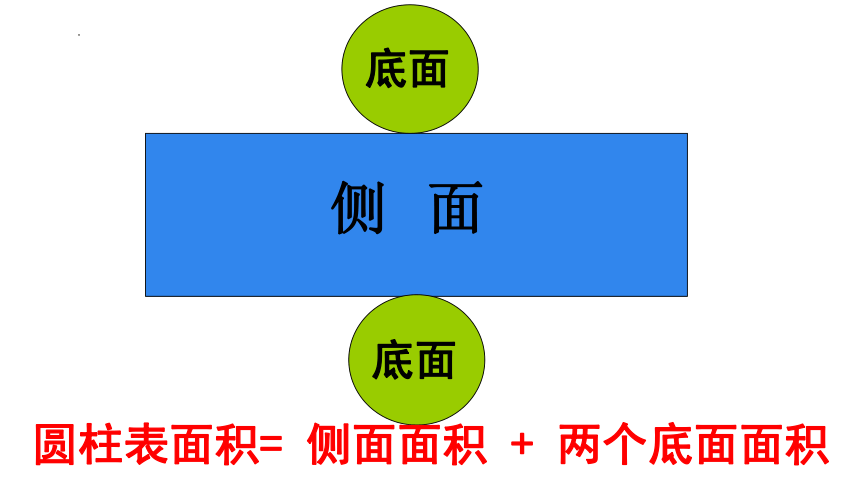
侧 面
底面
圆柱表面积= 侧面面积 + 两个底面面积
底面
合作交流
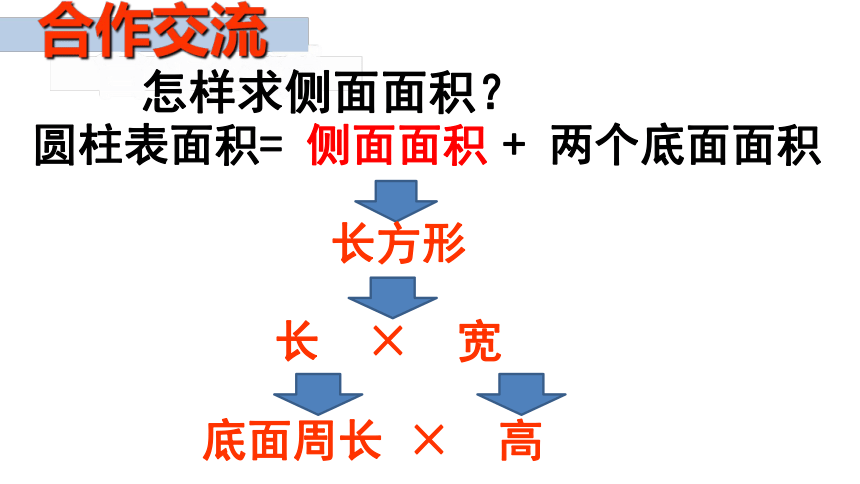
圆柱表面积= 侧面面积 + 两个底面面积
长方形
长 × 宽
底面周长 × 高
怎样求侧面面积?
动手实践
一个圆柱形茶叶筒的侧面贴着商标纸,圆柱底面半径是5cm,高是20cm。这张商标纸的面积是多少?
课本P21
动手实践
20
20
5
5
5
5
5
2
3.14
×
×
(1)侧面积:
(2)底面积:
(3)表面积:
2×3.14×5×20=628(平方厘米)
3.14×52×2=157(平方厘米)
628+157=785(平方厘米)
单位:厘米
在解答实际问题前一定要先进行分析,看它们求的是哪部分面积,再选择解答的方法。
一般分为3种情况:
1、有两个底面,一个侧面,如饼干盒,茶叶筒等;
2、只有一个底面和一个侧面,如无盖水桶,圆柱形鱼缸等;
3、两个底面都没有,只需计算侧面积,如水管,烟囱,轧路机轮等。
所以,在解答这些问题时,具体情况要具体对待。
联系生活实际,说说生活中的这些问题是求哪些面积?
⑴圆柱形水池的占地面积。( ) (填A.B.C.D)
⑵做一节烟囱所需铁皮面积。( )
⑶求易拉罐上商标纸的面积。( )
⑷做茶叶筒所需铁皮面积。( )
⑸做一个无盖水桶所需铁皮面积。( )
⑹压路机的滚筒转动一周,求压路面积。( )
A.求底面积 B.求1个底面积与侧面积
C.求侧面积 D.求表面积(2个底面积和侧面积)
A
C
C
D
B
C
一顶圆柱形厨师帽,高30㎝,冒顶直径是20㎝,做一顶帽子需要多少面料?(得数保留整十数)
注意:今后在计算原材料得数要求取近似数时,为了保证材料的够用,不能用四舍五入法,而必须用进一法。
解决问题
想想:应该求哪几个面?
做一个无盖的圆柱形铁皮水桶,高是5分米。底面直径4分米,至少需要多大面积的铁皮 (得数保留整十平方分米)
水桶没有盖,说明它只有一个底面。
(1)水桶的侧面积:
3.14 ×4 ×5=62.8(平方分米)
(2)水桶的底面积:
3.14 ×(4÷2)2=12.56(平方分米)
(3)需要铁皮:
62.8+12.56=75.36(平方分米)
一节圆柱形烟筒,底面直径是8厘米,长1.5米,做1000节这样的烟筒至少需要用白铁皮多少平方米?
S表=2πr×h + 2×πr2
计算原材料得数要求取近似数时,为了保证材料的够用,不能用四舍五入法,而必须用进一法。
课堂小结
解答实际问题前一定要先进行分析,看它们求的是哪部分面积,再选择解答的方法。
底面周长×高
圆柱的侧面积 + 两个底面的面积
圆柱的表面积=
每天进步一小步
十天进步一大步
圆柱的表面积
课前热身
1、圆柱有( )个底面,它们是( );
有( )侧面,是( ),有( )条高,
这些高都( )。
2、圆柱的侧面展开是( ),
长方形的长等于( ),宽是( )。
3、圆的面积公式=
4、圆的周长公式=
5、长方形的面积公式=
2
大小一样的圆
1
曲面
无数
长度相等
长方形或正方形
底面周长
圆柱的高
S=πr2
C=2πr
或C=πd
长×宽
做一个茶叶筒需要多大面积纸板
探究新知
说一说该求哪部分的面积。
茶叶
底面
底面
侧面
圆柱的侧面面积与两个底面面积的和,是圆柱的表面积。
圆柱的表面积:
探究新知
侧 面
底面
圆柱表面积= 侧面面积 + 两个底面面积
底面
合作交流
圆柱表面积= 侧面面积 + 两个底面面积
长方形
长 × 宽
底面周长 × 高
怎样求侧面面积?
动手实践
一个圆柱形茶叶筒的侧面贴着商标纸,圆柱底面半径是5cm,高是20cm。这张商标纸的面积是多少?
课本P21
动手实践
20
20
5
5
5
5
5
2
3.14
×
×
(1)侧面积:
(2)底面积:
(3)表面积:
2×3.14×5×20=628(平方厘米)
3.14×52×2=157(平方厘米)
628+157=785(平方厘米)
单位:厘米
在解答实际问题前一定要先进行分析,看它们求的是哪部分面积,再选择解答的方法。
一般分为3种情况:
1、有两个底面,一个侧面,如饼干盒,茶叶筒等;
2、只有一个底面和一个侧面,如无盖水桶,圆柱形鱼缸等;
3、两个底面都没有,只需计算侧面积,如水管,烟囱,轧路机轮等。
所以,在解答这些问题时,具体情况要具体对待。
联系生活实际,说说生活中的这些问题是求哪些面积?
⑴圆柱形水池的占地面积。( ) (填A.B.C.D)
⑵做一节烟囱所需铁皮面积。( )
⑶求易拉罐上商标纸的面积。( )
⑷做茶叶筒所需铁皮面积。( )
⑸做一个无盖水桶所需铁皮面积。( )
⑹压路机的滚筒转动一周,求压路面积。( )
A.求底面积 B.求1个底面积与侧面积
C.求侧面积 D.求表面积(2个底面积和侧面积)
A
C
C
D
B
C
一顶圆柱形厨师帽,高30㎝,冒顶直径是20㎝,做一顶帽子需要多少面料?(得数保留整十数)
注意:今后在计算原材料得数要求取近似数时,为了保证材料的够用,不能用四舍五入法,而必须用进一法。
解决问题
想想:应该求哪几个面?
做一个无盖的圆柱形铁皮水桶,高是5分米。底面直径4分米,至少需要多大面积的铁皮 (得数保留整十平方分米)
水桶没有盖,说明它只有一个底面。
(1)水桶的侧面积:
3.14 ×4 ×5=62.8(平方分米)
(2)水桶的底面积:
3.14 ×(4÷2)2=12.56(平方分米)
(3)需要铁皮:
62.8+12.56=75.36(平方分米)
一节圆柱形烟筒,底面直径是8厘米,长1.5米,做1000节这样的烟筒至少需要用白铁皮多少平方米?
S表=2πr×h + 2×πr2
计算原材料得数要求取近似数时,为了保证材料的够用,不能用四舍五入法,而必须用进一法。
课堂小结
解答实际问题前一定要先进行分析,看它们求的是哪部分面积,再选择解答的方法。
底面周长×高
圆柱的侧面积 + 两个底面的面积
圆柱的表面积=
每天进步一小步
十天进步一大步
