15.3 平行四边形的性质与判定 同步练习(含答案)2022-2023学年京改版八年级数学下册
文档属性
| 名称 | 15.3 平行四边形的性质与判定 同步练习(含答案)2022-2023学年京改版八年级数学下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 323.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-07 20:56:15 | ||
图片预览



文档简介
北京课改版八下 15.3 平行四边形的性质与判定
一、选择题(共12小题)
1. 在平行四边形 中,若 ,则 的度数是
A. B. C. D.
2. 为了估计鱼塘中鱼的条数,养鱼者先从鱼塘中捕获 条鱼,在每一条鱼身上做好标记后把这些鱼放归鱼塘,再从鱼塘中打捞鱼.通过多次实验发现捕捞的鱼有标记的频率稳定在 左右,则鱼塘中鱼的条数大约为
A. 条 B. 条 C. 条 D. 条
3. 平行四边形 中,若 ,则 的度数为
A. B. C. D.
4. 如图,小聪把一块含有 角的直角三角板的两个顶点放在直尺的对边上,并测得 ,则 的度数是
A. B. C. D.
5. 如图, 过平行四边形 对角线的交点 ,交 于点 ,交 于点 ,若平行四边形 的周长是 ,,则四边形 的周长为
A. B. C. D.
6. 如图,平行四边形 中, 、 是对角线 上不同的两点,下列条件中,不能得出四边形 一定为平行四边形的是
A. B.
C. D.
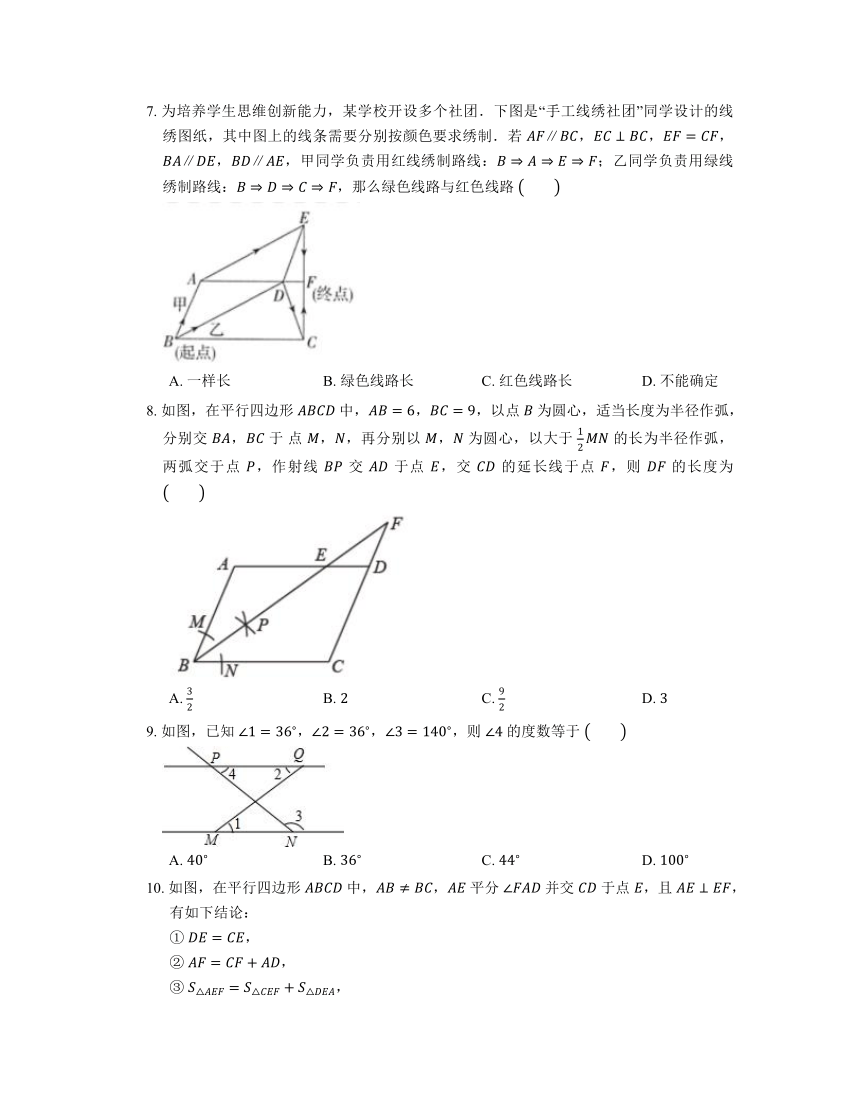
7. 为培养学生思维创新能力,某学校开设多个社团.下图是“手工线绣社团”同学设计的线绣图纸,其中图上的线条需要分别按颜色要求绣制.若 ,,,,,甲同学负责用红线绣制路线:;乙同学负责用绿线绣制路线:,那么绿色线路与红色线路
A. 一样长 B. 绿色线路长 C. 红色线路长 D. 不能确定
8. 如图,在平行四边形 中,,,以点 为圆心,适当长度为半径作弧,分别交 , 于 点 ,,再分别以 , 为圆心,以大于 的长为半径作弧,两弧交于点 ,作射线 交 于点 ,交 的延长线于点 ,则 的长度为
A. B. C. D.
9. 如图,已知 ,,,则 的度数等于
A. B. C. D.
10. 如图,在平行四边形 中,, 平分 并交 于点 ,且 ,有如下结论:
① ,
② ,
③ ,
④ ,
其中正确的是
A. ①④ B. ①②③ C. ②③④ D. ①②③④
11. 如图,在平行四边形 中,在对角线 上找点 ,,使四边形 为平行四边形,现有①,②,③三种方案,则正确的方案是
①只需要满足 ;
②只需要满足 ,;
③只需要满足 , 分别平分 ,.
A. ①②③ B. ①③ C. ①② D. ②③
12. 如图,已知直线 , 被直线 所截,,,则 的度数为
A. B. C. D.
二、填空题(共6小题)
13. 两组对边分别 的四边形叫做平行四边形.
14. 如图, 是平行四边形 的边 上一点,, 分别是 , 的中点,若平行四边形 的面积为 ,则 的面积(阴影部分)是 .
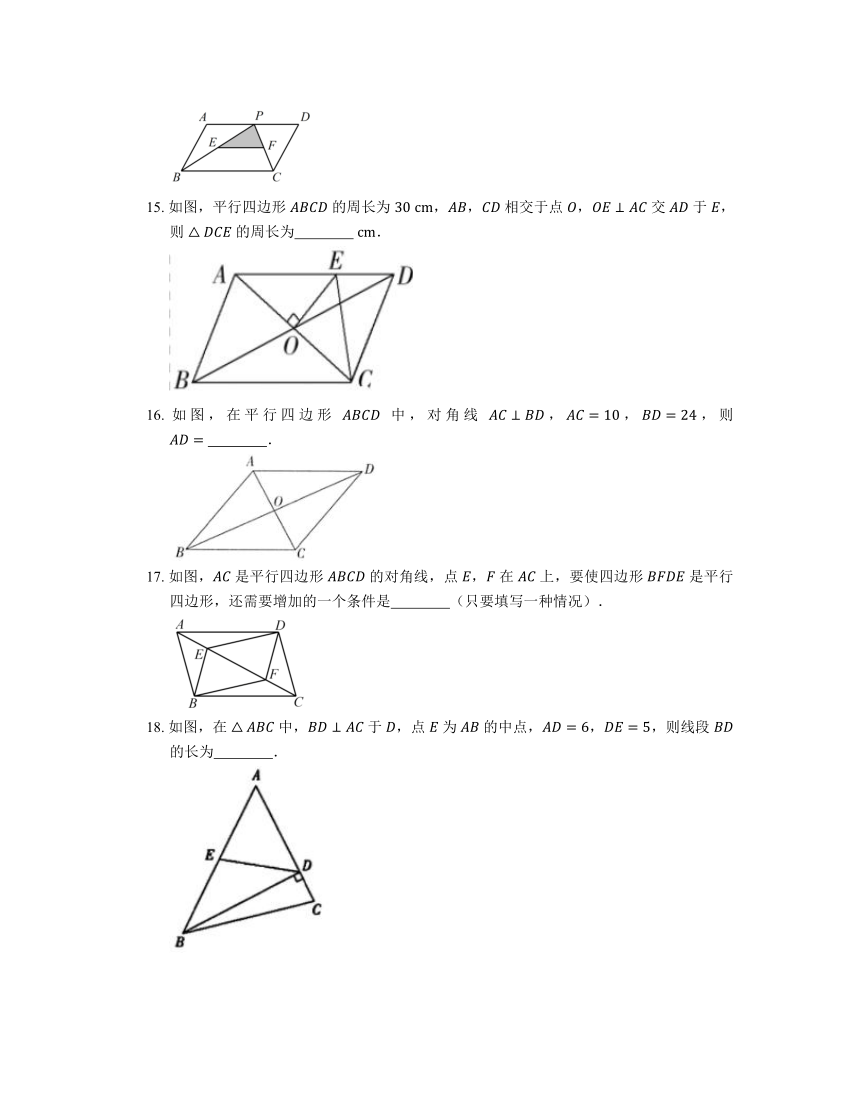
15. 如图,平行四边形 的周长为 ,, 相交于点 , 交 于 ,则 的周长为 .
16. 如图,在平行四边形 中,对角线 ,,,则 .
17. 如图, 是平行四边形 的对角线,点 , 在 上,要使四边形 是平行四边形,还需要增加的一个条件是 (只要填写一种情况).
18. 如图,在 中, 于 ,点 为 的中点,,,则线段 的长为 .
三、解答题(共6小题)
19. 如图,已知点 在线段 上,点 在线段 上,请在① ,② ,③ ,这三条信息中,选择其中的两条信息作为条件,剩下的条信息作为结论,编制一道试题,并给出解答.
20. 已知:如图在平行四边形 中点 , 分别是边 , 的中点.
求证:.
21. 如图,在 中,, 是 的中点,,.若 ,,求四边形 的周长.
22. 如图,四边形 是平行四边形,, 分别是 , 的平分线,且与对角线 分别相交于点 ,.求证: .
23. 已知:如图所示,,,.求证:.
24. 已知:如图,, 是平行四边形 对角线 上的两点,且 .求证:.
答案
一 选择题
1. C
【解析】 四边形 是平行四边形,
,
,
,
故选C.
2. B
3. A
4. C
【解析】
直尺的两边互相平行,,
,
.
5. B
【解析】 四边形 为平行四边形,对角线的交点为 ,
,,,,
.
在 和 中,
,
,,
平行四边形 的周长为 ,
,
.
故选B.
6. A
【解析】,无法判定四边形 ,故A选项符合题意;
如图,连接 ,
四边形 是平行四边形,
,,
,
,
四边形 是平行四边形,故选项B不符合题意;
四边形 是平行四边形,
,,,
,
在 和 中,
,
,
,
四边形 是平行四边形,故选项C不符合题意;
,
,
,
在 和 中,
,
,
,
四边形 是平行四边形,故选项D不符合题意;
故选:A.
7. A
【解析】由题意得四边形 是平行四边形,
,,
,,,
垂直平分 ,
,
,
绿色线路和红色线路一样长.
8. D
9. A
【解析】,,
,
,
.
10. B
11. A
【解析】① 四边形 是平行四边形,
,,
,
在 和 中,
,
,,
,
,
四边形 为平行四边形,故方案①正确;
② ,,
,,
在 和 中,
,
,
四边形 是平行四边形,故方案②正确;
③ 四边形 是平行四边形,
,,,
,
平分 , 平分 ,
,
在 和 中,
,
,,
,
,
四边形 为平行四边形,故方案③正确;
故选:A.
12. C
二 填空题
13. 平行
14.
【解析】 平行四边形 的面积为 ,
,
, 分别是 , 的中点,
,且 ,
,
,即 ,
.
15.
16.
【解析】 平行四边形 的对角线 与 相交于点 ,
,,
,
.
17. 等
18.
【解析】 于 ,点 为 的中点,
,
在 中,.
三 解答题
19. 条件:①②;结论:③.
证明过程如下:
,
,
内错角相等,两直线平行,
,
两直线平行,内错角相等,
又 ,
,
,
同位角相等,两直线平行.
20. 四边形 是平行四边形,
,,,
点 , 分别是边 , 的中点,
,,
,
在 和 中,
,
.
21. ,,
.
又 ,
四边形 是平行四边形.
.
在 中,由勾股定理得 .
是 的中点,
.
在 中,.
由勾股定理得 .
是 的中点,,
.
.
22. 因为四边形 是平行四边形,
所以 ,,,
所以 ,
又因为 , 分别是 , 的平分线,
所以 ,,
所以 ,
所以 ,
所以 .
23. 提示:取 的中点 ,连接 ,证 .
24. 四边形 是平行四边形,
,,
,
又 .
.
一、选择题(共12小题)
1. 在平行四边形 中,若 ,则 的度数是
A. B. C. D.
2. 为了估计鱼塘中鱼的条数,养鱼者先从鱼塘中捕获 条鱼,在每一条鱼身上做好标记后把这些鱼放归鱼塘,再从鱼塘中打捞鱼.通过多次实验发现捕捞的鱼有标记的频率稳定在 左右,则鱼塘中鱼的条数大约为
A. 条 B. 条 C. 条 D. 条
3. 平行四边形 中,若 ,则 的度数为
A. B. C. D.
4. 如图,小聪把一块含有 角的直角三角板的两个顶点放在直尺的对边上,并测得 ,则 的度数是
A. B. C. D.
5. 如图, 过平行四边形 对角线的交点 ,交 于点 ,交 于点 ,若平行四边形 的周长是 ,,则四边形 的周长为
A. B. C. D.
6. 如图,平行四边形 中, 、 是对角线 上不同的两点,下列条件中,不能得出四边形 一定为平行四边形的是
A. B.
C. D.
7. 为培养学生思维创新能力,某学校开设多个社团.下图是“手工线绣社团”同学设计的线绣图纸,其中图上的线条需要分别按颜色要求绣制.若 ,,,,,甲同学负责用红线绣制路线:;乙同学负责用绿线绣制路线:,那么绿色线路与红色线路
A. 一样长 B. 绿色线路长 C. 红色线路长 D. 不能确定
8. 如图,在平行四边形 中,,,以点 为圆心,适当长度为半径作弧,分别交 , 于 点 ,,再分别以 , 为圆心,以大于 的长为半径作弧,两弧交于点 ,作射线 交 于点 ,交 的延长线于点 ,则 的长度为
A. B. C. D.
9. 如图,已知 ,,,则 的度数等于
A. B. C. D.
10. 如图,在平行四边形 中,, 平分 并交 于点 ,且 ,有如下结论:
① ,
② ,
③ ,
④ ,
其中正确的是
A. ①④ B. ①②③ C. ②③④ D. ①②③④
11. 如图,在平行四边形 中,在对角线 上找点 ,,使四边形 为平行四边形,现有①,②,③三种方案,则正确的方案是
①只需要满足 ;
②只需要满足 ,;
③只需要满足 , 分别平分 ,.
A. ①②③ B. ①③ C. ①② D. ②③
12. 如图,已知直线 , 被直线 所截,,,则 的度数为
A. B. C. D.
二、填空题(共6小题)
13. 两组对边分别 的四边形叫做平行四边形.
14. 如图, 是平行四边形 的边 上一点,, 分别是 , 的中点,若平行四边形 的面积为 ,则 的面积(阴影部分)是 .
15. 如图,平行四边形 的周长为 ,, 相交于点 , 交 于 ,则 的周长为 .
16. 如图,在平行四边形 中,对角线 ,,,则 .
17. 如图, 是平行四边形 的对角线,点 , 在 上,要使四边形 是平行四边形,还需要增加的一个条件是 (只要填写一种情况).
18. 如图,在 中, 于 ,点 为 的中点,,,则线段 的长为 .
三、解答题(共6小题)
19. 如图,已知点 在线段 上,点 在线段 上,请在① ,② ,③ ,这三条信息中,选择其中的两条信息作为条件,剩下的条信息作为结论,编制一道试题,并给出解答.
20. 已知:如图在平行四边形 中点 , 分别是边 , 的中点.
求证:.
21. 如图,在 中,, 是 的中点,,.若 ,,求四边形 的周长.
22. 如图,四边形 是平行四边形,, 分别是 , 的平分线,且与对角线 分别相交于点 ,.求证: .
23. 已知:如图所示,,,.求证:.
24. 已知:如图,, 是平行四边形 对角线 上的两点,且 .求证:.
答案
一 选择题
1. C
【解析】 四边形 是平行四边形,
,
,
,
故选C.
2. B
3. A
4. C
【解析】
直尺的两边互相平行,,
,
.
5. B
【解析】 四边形 为平行四边形,对角线的交点为 ,
,,,,
.
在 和 中,
,
,,
平行四边形 的周长为 ,
,
.
故选B.
6. A
【解析】,无法判定四边形 ,故A选项符合题意;
如图,连接 ,
四边形 是平行四边形,
,,
,
,
四边形 是平行四边形,故选项B不符合题意;
四边形 是平行四边形,
,,,
,
在 和 中,
,
,
,
四边形 是平行四边形,故选项C不符合题意;
,
,
,
在 和 中,
,
,
,
四边形 是平行四边形,故选项D不符合题意;
故选:A.
7. A
【解析】由题意得四边形 是平行四边形,
,,
,,,
垂直平分 ,
,
,
绿色线路和红色线路一样长.
8. D
9. A
【解析】,,
,
,
.
10. B
11. A
【解析】① 四边形 是平行四边形,
,,
,
在 和 中,
,
,,
,
,
四边形 为平行四边形,故方案①正确;
② ,,
,,
在 和 中,
,
,
四边形 是平行四边形,故方案②正确;
③ 四边形 是平行四边形,
,,,
,
平分 , 平分 ,
,
在 和 中,
,
,,
,
,
四边形 为平行四边形,故方案③正确;
故选:A.
12. C
二 填空题
13. 平行
14.
【解析】 平行四边形 的面积为 ,
,
, 分别是 , 的中点,
,且 ,
,
,即 ,
.
15.
16.
【解析】 平行四边形 的对角线 与 相交于点 ,
,,
,
.
17. 等
18.
【解析】 于 ,点 为 的中点,
,
在 中,.
三 解答题
19. 条件:①②;结论:③.
证明过程如下:
,
,
内错角相等,两直线平行,
,
两直线平行,内错角相等,
又 ,
,
,
同位角相等,两直线平行.
20. 四边形 是平行四边形,
,,,
点 , 分别是边 , 的中点,
,,
,
在 和 中,
,
.
21. ,,
.
又 ,
四边形 是平行四边形.
.
在 中,由勾股定理得 .
是 的中点,
.
在 中,.
由勾股定理得 .
是 的中点,,
.
.
22. 因为四边形 是平行四边形,
所以 ,,,
所以 ,
又因为 , 分别是 , 的平分线,
所以 ,,
所以 ,
所以 ,
所以 .
23. 提示:取 的中点 ,连接 ,证 .
24. 四边形 是平行四边形,
,,
,
又 .
.
同课章节目录
