2022—2023学年人教版数学八年级下册18.1.2平行四边形的判定解答题(无答案)
文档属性
| 名称 | 2022—2023学年人教版数学八年级下册18.1.2平行四边形的判定解答题(无答案) |  | |
| 格式 | docx | ||
| 文件大小 | 130.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-07 21:03:33 | ||
图片预览

文档简介
18.1.2平行四边形的判定(解答题)
姓名: 得分: 日期:
1、已知:如图所示, ABCD中,E、F分别是AB、CD的中点:
(1)求证: ≌ ;(2)四边形AECF是平行四边形.
2、如图,D是 的边AB上一点, 交AC于点F,若FA=FC.
(1)求证:四边形ADCE是平行四边形;
(2)若AE⊥EC,EF=EC=1,求四边形ADCE的面积.
3、如图,在 中,AE平分∠BAC,BE⊥AE于点E,点F是BC的中点.
(1)如图1,BE的延长线与AC边相交于点D,求证: ;
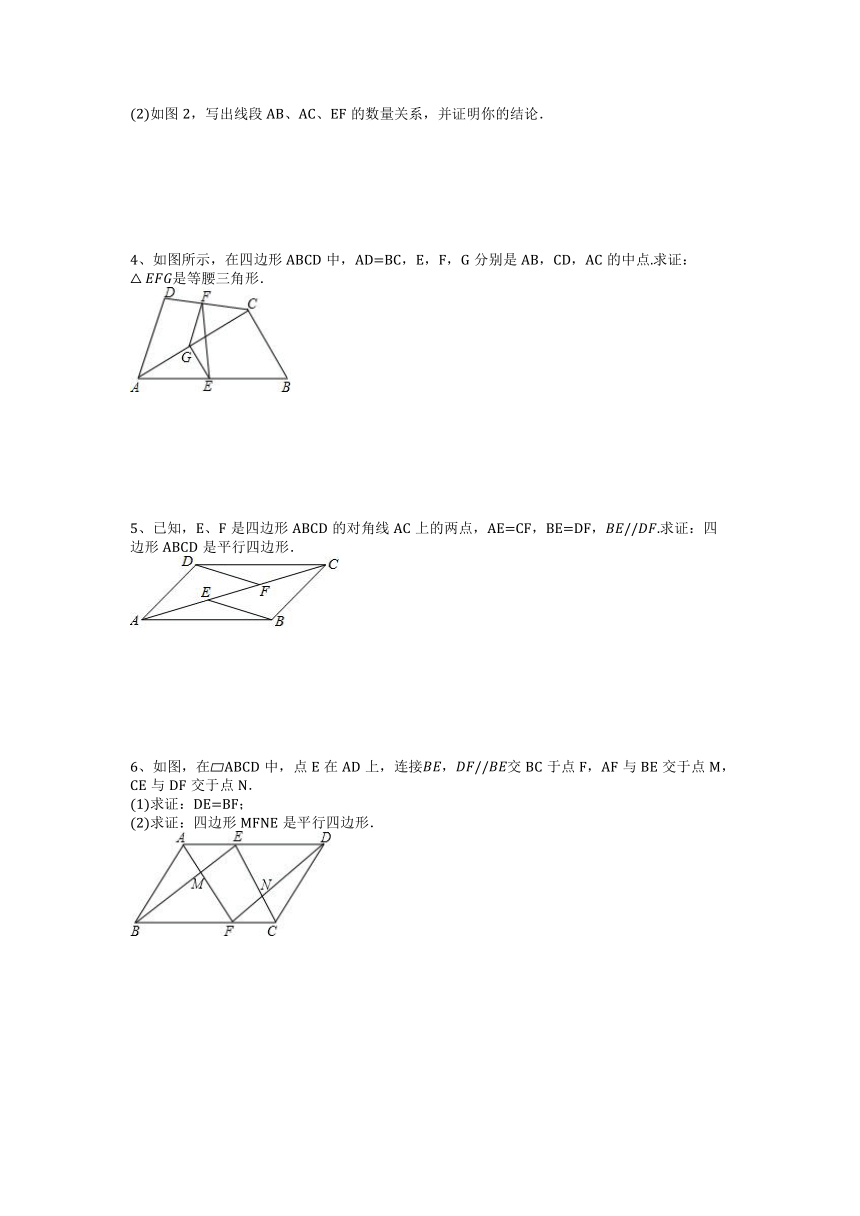
(2)如图2,写出线段AB、AC、EF的数量关系,并证明你的结论.
4、如图所示,在四边形ABCD中,AD=BC,E,F,G分别是AB,CD,AC的中点.求证: 是等腰三角形.
5、已知,E、F是四边形ABCD的对角线AC上的两点,AE=CF,BE=DF, 求证:四边形ABCD是平行四边形.
6、如图,在 ABCD中,点E在AD上,连接 交BC于点F,AF与BE交于点M,CE与DF交于点N.
(1)求证:DE=BF;
(2)求证:四边形MFNE是平行四边形.
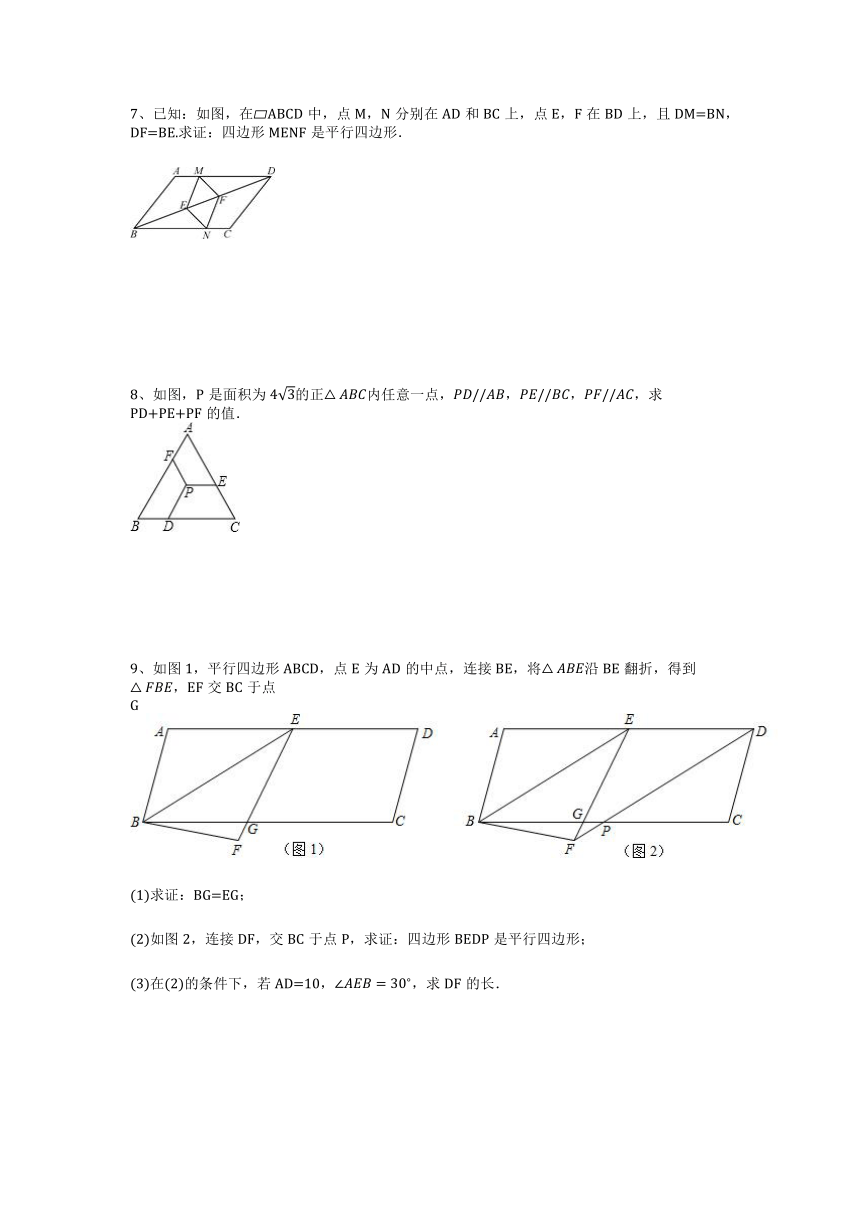
7、已知:如图,在 ABCD中,点M,N分别在AD和BC上,点E,F在BD上,且DM=BN,DF=BE.求证:四边形MENF是平行四边形.
8、如图,P是面积为 的正 内任意一点, ,求PD+PE+PF的值.
9、如图1,平行四边形ABCD,点E为AD的中点,连接BE,将 沿BE翻折,得到 ,EF交BC于点G
(1)求证:BG=EG;
(2)如图2,连接DF,交BC于点P,求证:四边形BEDP是平行四边形;
(3)在(2)的条件下,若AD=10, ,求DF的长.
10、如图,点O是 内一点,连接OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连接,得到四边形DEFG.
(1)求证:四边形DEFG是平行四边形;
(2)如果 , ,OC=4,求EF的长.
11、已知:如图,平行四边形ABCD, E、F是直线AC上两点,且AE=CF求证:四边形EBFD为平行四边形.
12、如图,BD是 的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.
(1)请判断四边形EBGD的形状,并说明理由;
(2)若 ,点H是BD上的一个动点,求HG+HC的最小值.
13、 如图所示,直线 与x轴、y轴交于A、B两点,点C是y轴负半轴上一点,BA=BC.
(1)求 的面积和点C的坐标;
(2)在平面内是否存在点P,使以P,A,B,C为顶点的四边形为平行四边形 若存在,请直接写出所有的点P的坐标;若不存在,请说明理由.
14、 如图,在四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点, ,∠ABC=∠ADC,CD =3,求OE的长.
15、如图,已知在 是等边三角形,点D、F分别在线段BC、AB上, ,EF=DC
(1)求证:四边形EFCD是平行四边形;
(2)若BF=EF,求证:AE=AD.
16、(10分) 如图,在 Rt ABC中,∠ C , BC=8, AC=6,动点 P从点 A开始,沿边 AC向点 C以每秒1个单位长度的速度运动,动点 D从点 A开始,沿边 AB向点 B以每秒 个单位长度的速度运动,且恰好能始终保持连结两动点的直线 PD⊥ AC,动点 Q从点 C开始,沿边 CB向点 B以每秒2个单位长度的速度运动,连结 PQ.点 P, D, Q分别从点 A, C同时出发,当其中一点到达端点时,另两个点也随之停止运动,设运动时间为 t秒( t .
(1)当 t为何值时,四边形 BQPD的面积为 ABC面积的一半?
(2)当四边形 PDBQ为平行四边形时,求出 t的值。
17、如图,AM是 的中线,D是线段AM上一点(不与点A重合 交AC于点F, ,连结AE.
(1)如图1,当点D与M重合时,求证:四边形ABDE是平行四边形;
(2)如图2,当点D不与M重合时,(1)中的结论还成立吗?请说明理由.
(3)如图3,延长BD交AC于点H,若BH⊥AC,且BH=AM.
①求∠CAM的度数;
②当 ,DM=4时,求DH的长.
18、(本题6分)已知 , , 均为直线BC的同侧的正三角形.
求证:四边形ADEF为平行四边形
姓名: 得分: 日期:
1、已知:如图所示, ABCD中,E、F分别是AB、CD的中点:
(1)求证: ≌ ;(2)四边形AECF是平行四边形.
2、如图,D是 的边AB上一点, 交AC于点F,若FA=FC.
(1)求证:四边形ADCE是平行四边形;
(2)若AE⊥EC,EF=EC=1,求四边形ADCE的面积.
3、如图,在 中,AE平分∠BAC,BE⊥AE于点E,点F是BC的中点.
(1)如图1,BE的延长线与AC边相交于点D,求证: ;
(2)如图2,写出线段AB、AC、EF的数量关系,并证明你的结论.
4、如图所示,在四边形ABCD中,AD=BC,E,F,G分别是AB,CD,AC的中点.求证: 是等腰三角形.
5、已知,E、F是四边形ABCD的对角线AC上的两点,AE=CF,BE=DF, 求证:四边形ABCD是平行四边形.
6、如图,在 ABCD中,点E在AD上,连接 交BC于点F,AF与BE交于点M,CE与DF交于点N.
(1)求证:DE=BF;
(2)求证:四边形MFNE是平行四边形.
7、已知:如图,在 ABCD中,点M,N分别在AD和BC上,点E,F在BD上,且DM=BN,DF=BE.求证:四边形MENF是平行四边形.
8、如图,P是面积为 的正 内任意一点, ,求PD+PE+PF的值.
9、如图1,平行四边形ABCD,点E为AD的中点,连接BE,将 沿BE翻折,得到 ,EF交BC于点G
(1)求证:BG=EG;
(2)如图2,连接DF,交BC于点P,求证:四边形BEDP是平行四边形;
(3)在(2)的条件下,若AD=10, ,求DF的长.
10、如图,点O是 内一点,连接OB、OC,并将AB、OB、OC、AC的中点D、E、F、G依次连接,得到四边形DEFG.
(1)求证:四边形DEFG是平行四边形;
(2)如果 , ,OC=4,求EF的长.
11、已知:如图,平行四边形ABCD, E、F是直线AC上两点,且AE=CF求证:四边形EBFD为平行四边形.
12、如图,BD是 的角平分线,它的垂直平分线分别交AB,BD,BC于点E,F,G,连接ED,DG.
(1)请判断四边形EBGD的形状,并说明理由;
(2)若 ,点H是BD上的一个动点,求HG+HC的最小值.
13、 如图所示,直线 与x轴、y轴交于A、B两点,点C是y轴负半轴上一点,BA=BC.
(1)求 的面积和点C的坐标;
(2)在平面内是否存在点P,使以P,A,B,C为顶点的四边形为平行四边形 若存在,请直接写出所有的点P的坐标;若不存在,请说明理由.
14、 如图,在四边形ABCD中,对角线AC、BD交于点O,点E是BC的中点, ,∠ABC=∠ADC,CD =3,求OE的长.
15、如图,已知在 是等边三角形,点D、F分别在线段BC、AB上, ,EF=DC
(1)求证:四边形EFCD是平行四边形;
(2)若BF=EF,求证:AE=AD.
16、(10分) 如图,在 Rt ABC中,∠ C , BC=8, AC=6,动点 P从点 A开始,沿边 AC向点 C以每秒1个单位长度的速度运动,动点 D从点 A开始,沿边 AB向点 B以每秒 个单位长度的速度运动,且恰好能始终保持连结两动点的直线 PD⊥ AC,动点 Q从点 C开始,沿边 CB向点 B以每秒2个单位长度的速度运动,连结 PQ.点 P, D, Q分别从点 A, C同时出发,当其中一点到达端点时,另两个点也随之停止运动,设运动时间为 t秒( t .
(1)当 t为何值时,四边形 BQPD的面积为 ABC面积的一半?
(2)当四边形 PDBQ为平行四边形时,求出 t的值。
17、如图,AM是 的中线,D是线段AM上一点(不与点A重合 交AC于点F, ,连结AE.
(1)如图1,当点D与M重合时,求证:四边形ABDE是平行四边形;
(2)如图2,当点D不与M重合时,(1)中的结论还成立吗?请说明理由.
(3)如图3,延长BD交AC于点H,若BH⊥AC,且BH=AM.
①求∠CAM的度数;
②当 ,DM=4时,求DH的长.
18、(本题6分)已知 , , 均为直线BC的同侧的正三角形.
求证:四边形ADEF为平行四边形
