2022—2023学年华东师大版八年级数学下册18.1 平行四边形的性质 同步练习(含答案)
文档属性
| 名称 | 2022—2023学年华东师大版八年级数学下册18.1 平行四边形的性质 同步练习(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-08 07:40:52 | ||
图片预览

文档简介
华师大版八下 18.1 平行四边形的性质
一、(共18小题)
1. 在平行四边形 中,,则
A. B. C. D.
2. 如图,将平行四边形 的一边 延长至点 ,若 ,则 等于
A. B. C. D.
3. 在同一平面内,设 ,, 是三条互相平行的直线,已知 与 的距离为 , 与 的距离为 ,则 与 的距离为
A. B. C. 或 D. 或
4. 如图,平行四边形 的周长为 ,,, 相交于点 , 交 于点 ,则 的周长为
A. B. C. D.
5. 已知直线 ,点 在 上,点 ,, 在 上,且 ,,,则 与 之间的距离
A. 等于 B. 等于
C. 等于 D. 小于或等于
6. 如图,点 是平行四边形 的边 延长线上一点,下列结论不一定成立的是
A. B.
C. D.
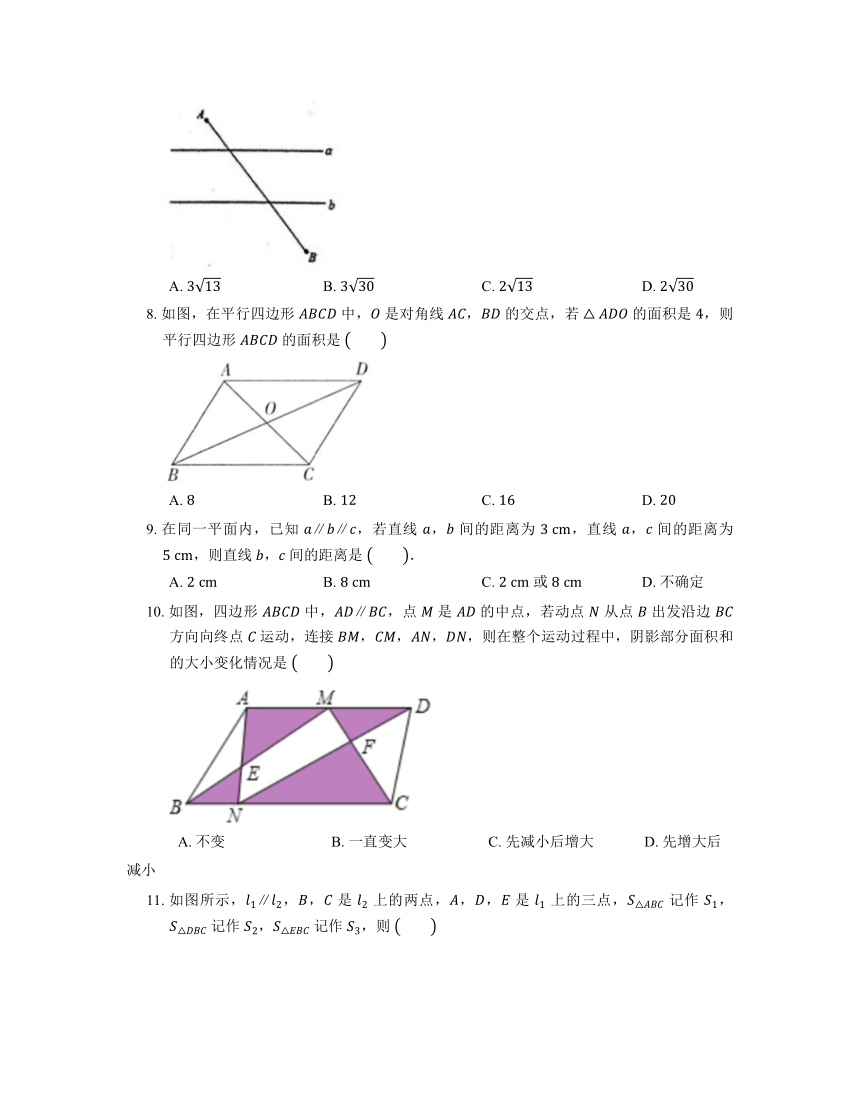
7. 如图,已知直线 ,且 与 之间的距离为 ,点 到直线 的距离为 ,点 到直线 的距离为 ,试在直线 上找一点 ,直线 上找一点 ,满足 , 的长度和最短,且 .则 长
A. B. C. D.
8. 如图,在平行四边形 中, 是对角线 , 的交点,若 的面积是 ,则平行四边形 的面积是
A. B. C. D.
9. 在同一平面内,已知 ,若直线 , 间的距离为 ,直线 , 间的距离为 ,则直线 , 间的距离是 .
A. B. C. 或 D. 不确定
10. 如图,四边形 中,,点 是 的中点,若动点 从点 出发沿边 方向向终点 运动,连接 ,,,,则在整个运动过程中,阴影部分面积和的大小变化情况是
A. 不变 B. 一直变大 C. 先减小后增大 D. 先增大后减小
11. 如图所示,,, 是 上的两点,,, 是 上的三点, 记作 , 记作 , 记作 ,则
A. B. C. D. 无法比较
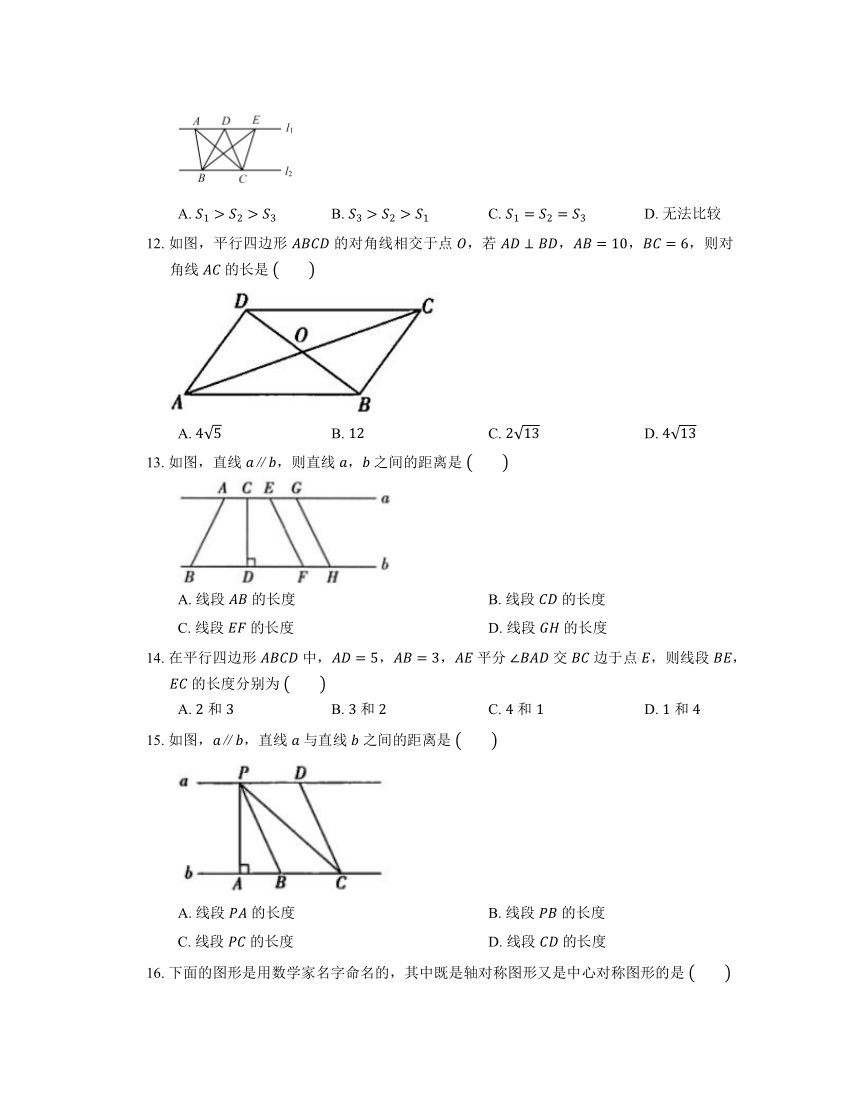
12. 如图,平行四边形 的对角线相交于点 ,若 ,,,则对角线 的长是
A. B. C. D.
13. 如图,直线 ,则直线 , 之间的距离是
A. 线段 的长度 B. 线段 的长度
C. 线段 的长度 D. 线段 的长度
14. 在平行四边形 中,,, 平分 交 边于点 ,则线段 , 的长度分别为
A. 和 B. 和 C. 和 D. 和
15. 如图,,直线 与直线 之间的距离是
A. 线段 的长度 B. 线段 的长度
C. 线段 的长度 D. 线段 的长度
16. 下面的图形是用数学家名字命名的,其中既是轴对称图形又是中心对称图形的是
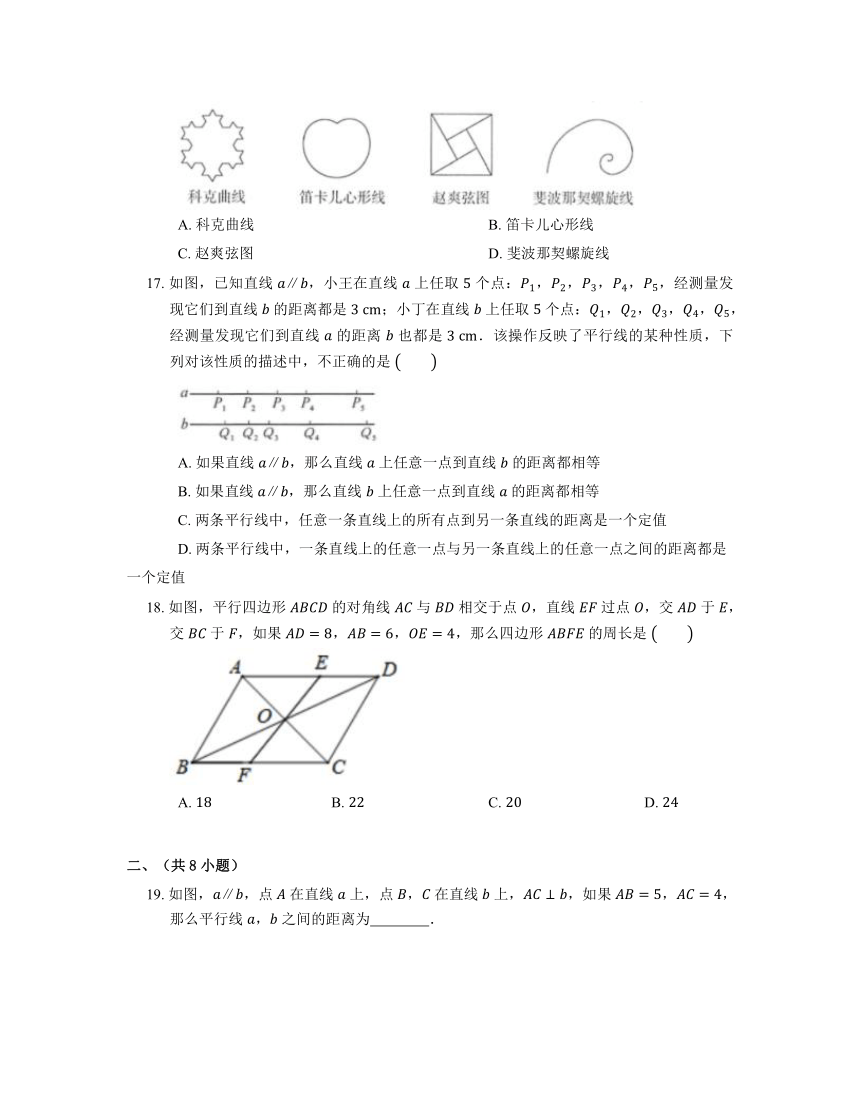
A. 科克曲线 B. 笛卡儿心形线
C. 赵爽弦图 D. 斐波那契螺旋线
17. 如图,已知直线 ,小王在直线 上任取 个点:,,,,,经测量发现它们到直线 的距离都是 ;小丁在直线 上任取 个点:,,,,,经测量发现它们到直线 的距离 也都是 .该操作反映了平行线的某种性质,下列对该性质的描述中,不正确的是
A. 如果直线 ,那么直线 上任意一点到直线 的距离都相等
B. 如果直线 ,那么直线 上任意一点到直线 的距离都相等
C. 两条平行线中,任意一条直线上的所有点到另一条直线的距离是一个定值
D. 两条平行线中,一条直线上的任意一点与另一条直线上的任意一点之间的距离都是一个定值
18. 如图,平行四边形 的对角线 与 相交于点 ,直线 过点 ,交 于 ,交 于 ,如果 ,,,那么四边形 的周长是
A. B. C. D.
二、(共8小题)
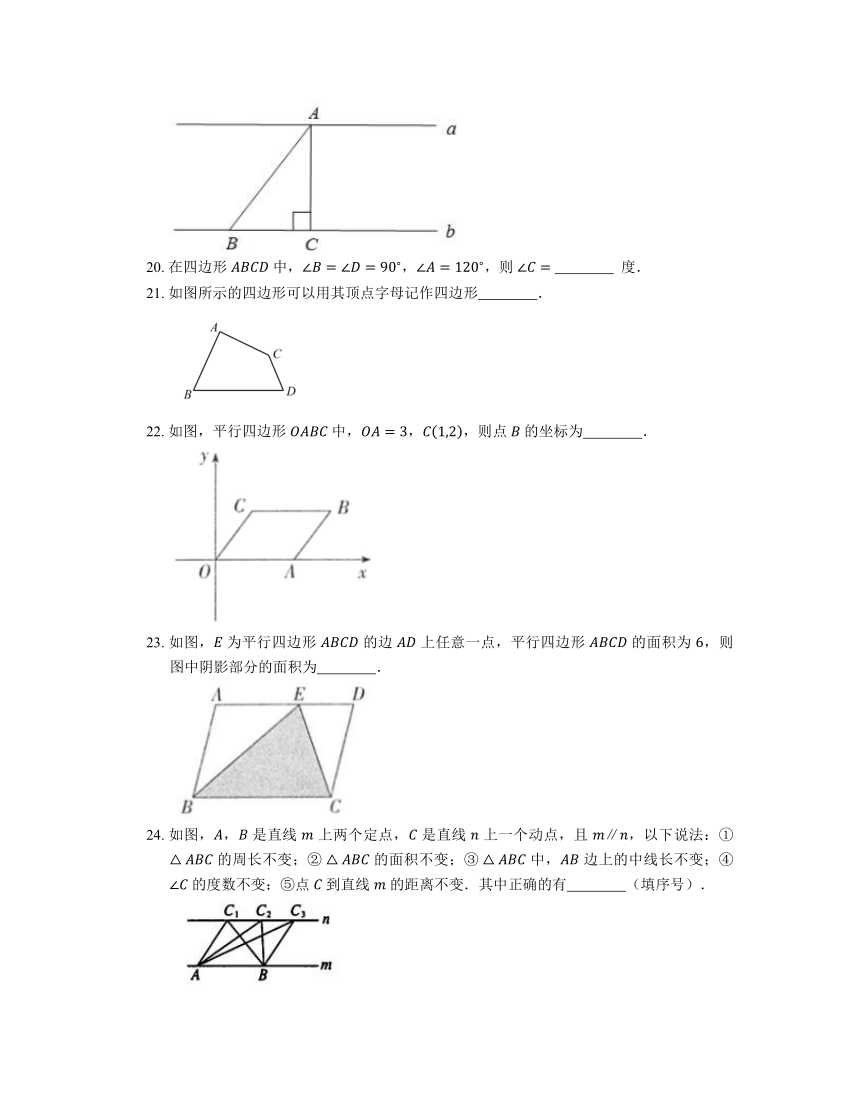
19. 如图,,点 在直线 上,点 , 在直线 上,,如果 ,,那么平行线 , 之间的距离为 .
20. 在四边形 中,,,则 度.
21. 如图所示的四边形可以用其顶点字母记作四边形 .
22. 如图,平行四边形 中,,,则点 的坐标为 .
23. 如图, 为平行四边形 的边 上任意一点,平行四边形 的面积为 ,则图中阴影部分的面积为 .
24. 如图,, 是直线 上两个定点, 是直线 上一个动点,且 ,以下说法:① 的周长不变;② 的面积不变;③ 中, 边上的中线长不变;④ 的度数不变;⑤点 到直线 的距离不变.其中正确的有 (填序号).
25. 如图所示,点 ,, 分别在 的三边 ,, 上,且 ,,,则图中共有 个平行四边形,分别为 .
26. 如图,在平行四边形 中,对角线 ,,,则 .
三、(共5小题)
27. 如图,平行四边形 和平行四边形 的顶点 ,,, 在同一直线上,求证:.
28. 如图,已知点 , 分别在长方形 的边 , 上,且 .请分别度量 与 之间的距离, 与 之间的距离(精确到 ).
29. 如图,在 中,, 是 边上任意一点, 于点 , 于点 , 为 的高线,.
(1)求 的值.
30. 为了表示几种三角形之间的关系,画了如图所示的结构图,请你采用适当的方式表示正方形、平行四边形、四边形、菱形、矩形之间的关系.
31. 已知:如图,点 在线段 上, 平分 ,,,.求证:.
答案
一
1. B
2. B
【解析】 平行四边形 的 ,
,
.
故选:B.
3. C
4. D
5. D
6. D
【解析】A.在平行四边形 中,,故A结论正确.
B.在平行四边形 中,,
,
,
,
,
,故B结论正确.
C.在平行四边形 中,,故C结论正确.
D.在平行四边形 中,,
,故D结论不一定成立.故选D.
7. D
8. C
【解析】因为平行四边形的对角线互相平分,
所以 ,,则 与 是等底同高的三角形,
所以 与 的面积相等,
同理, 与 的面积相等.
因此 ,,, 的面积都相等,
所以 .
9. C
10. A
【解析】连接 ,过 作 于 ,交 于 ,过 作 于 ,交 于 ,
,
,
,
,
,
阴影部分面积 ,
阴影部分面积不变.
11. C
【解析】同底等高的三角形的面积相等.
12. D
【解析】 四边形 是平行四边形,
,
,,
,
四边形 是平行四边形,
,,
,
,
.
13. B
【解析】平行线间的距离为平行线上一点到另一条平行线的垂线段的长度.
故选B.
14. B
15. A
【解析】由题图可得,,
又因为 ,
所以线段 的长度是直线 与直线 之间的距离,故选A.
16. A
【解析】选项B是轴对称图形不是中心对称图形,选项C是中心对称图形不是轴对称图形,选项D既不是轴对称图形又不是中心对称图形.故选A.
17. D
18. B
二
19.
20.
21. (或 )
22.
【解析】 四边形 是平行四边形,,
,,
点 的坐标为 ,
点 的坐标为 .
23.
【解析】 平行四边形 的面积为 ,
24. ②⑤
25. ,平行四边形 ,平行四边形 ,平行四边形
26.
【解析】 平行四边形 的对角线 与 相交于点 ,
,,
,
.
三
27. 连接 交 于点 ,
则 ,,
.
28. 过点 作 于点 .
经测量可得:,,则 与 之间的距离是 , 与 之间的距离是 .
29. 连接 .
由图形可知:,
即 .
,
,
.
30. 如图所示(答案不唯一).
31. ,
.
在 和 中,
,
,
是等腰三角形.
平分 ,
.
一、(共18小题)
1. 在平行四边形 中,,则
A. B. C. D.
2. 如图,将平行四边形 的一边 延长至点 ,若 ,则 等于
A. B. C. D.
3. 在同一平面内,设 ,, 是三条互相平行的直线,已知 与 的距离为 , 与 的距离为 ,则 与 的距离为
A. B. C. 或 D. 或
4. 如图,平行四边形 的周长为 ,,, 相交于点 , 交 于点 ,则 的周长为
A. B. C. D.
5. 已知直线 ,点 在 上,点 ,, 在 上,且 ,,,则 与 之间的距离
A. 等于 B. 等于
C. 等于 D. 小于或等于
6. 如图,点 是平行四边形 的边 延长线上一点,下列结论不一定成立的是
A. B.
C. D.
7. 如图,已知直线 ,且 与 之间的距离为 ,点 到直线 的距离为 ,点 到直线 的距离为 ,试在直线 上找一点 ,直线 上找一点 ,满足 , 的长度和最短,且 .则 长
A. B. C. D.
8. 如图,在平行四边形 中, 是对角线 , 的交点,若 的面积是 ,则平行四边形 的面积是
A. B. C. D.
9. 在同一平面内,已知 ,若直线 , 间的距离为 ,直线 , 间的距离为 ,则直线 , 间的距离是 .
A. B. C. 或 D. 不确定
10. 如图,四边形 中,,点 是 的中点,若动点 从点 出发沿边 方向向终点 运动,连接 ,,,,则在整个运动过程中,阴影部分面积和的大小变化情况是
A. 不变 B. 一直变大 C. 先减小后增大 D. 先增大后减小
11. 如图所示,,, 是 上的两点,,, 是 上的三点, 记作 , 记作 , 记作 ,则
A. B. C. D. 无法比较
12. 如图,平行四边形 的对角线相交于点 ,若 ,,,则对角线 的长是
A. B. C. D.
13. 如图,直线 ,则直线 , 之间的距离是
A. 线段 的长度 B. 线段 的长度
C. 线段 的长度 D. 线段 的长度
14. 在平行四边形 中,,, 平分 交 边于点 ,则线段 , 的长度分别为
A. 和 B. 和 C. 和 D. 和
15. 如图,,直线 与直线 之间的距离是
A. 线段 的长度 B. 线段 的长度
C. 线段 的长度 D. 线段 的长度
16. 下面的图形是用数学家名字命名的,其中既是轴对称图形又是中心对称图形的是
A. 科克曲线 B. 笛卡儿心形线
C. 赵爽弦图 D. 斐波那契螺旋线
17. 如图,已知直线 ,小王在直线 上任取 个点:,,,,,经测量发现它们到直线 的距离都是 ;小丁在直线 上任取 个点:,,,,,经测量发现它们到直线 的距离 也都是 .该操作反映了平行线的某种性质,下列对该性质的描述中,不正确的是
A. 如果直线 ,那么直线 上任意一点到直线 的距离都相等
B. 如果直线 ,那么直线 上任意一点到直线 的距离都相等
C. 两条平行线中,任意一条直线上的所有点到另一条直线的距离是一个定值
D. 两条平行线中,一条直线上的任意一点与另一条直线上的任意一点之间的距离都是一个定值
18. 如图,平行四边形 的对角线 与 相交于点 ,直线 过点 ,交 于 ,交 于 ,如果 ,,,那么四边形 的周长是
A. B. C. D.
二、(共8小题)
19. 如图,,点 在直线 上,点 , 在直线 上,,如果 ,,那么平行线 , 之间的距离为 .
20. 在四边形 中,,,则 度.
21. 如图所示的四边形可以用其顶点字母记作四边形 .
22. 如图,平行四边形 中,,,则点 的坐标为 .
23. 如图, 为平行四边形 的边 上任意一点,平行四边形 的面积为 ,则图中阴影部分的面积为 .
24. 如图,, 是直线 上两个定点, 是直线 上一个动点,且 ,以下说法:① 的周长不变;② 的面积不变;③ 中, 边上的中线长不变;④ 的度数不变;⑤点 到直线 的距离不变.其中正确的有 (填序号).
25. 如图所示,点 ,, 分别在 的三边 ,, 上,且 ,,,则图中共有 个平行四边形,分别为 .
26. 如图,在平行四边形 中,对角线 ,,,则 .
三、(共5小题)
27. 如图,平行四边形 和平行四边形 的顶点 ,,, 在同一直线上,求证:.
28. 如图,已知点 , 分别在长方形 的边 , 上,且 .请分别度量 与 之间的距离, 与 之间的距离(精确到 ).
29. 如图,在 中,, 是 边上任意一点, 于点 , 于点 , 为 的高线,.
(1)求 的值.
30. 为了表示几种三角形之间的关系,画了如图所示的结构图,请你采用适当的方式表示正方形、平行四边形、四边形、菱形、矩形之间的关系.
31. 已知:如图,点 在线段 上, 平分 ,,,.求证:.
答案
一
1. B
2. B
【解析】 平行四边形 的 ,
,
.
故选:B.
3. C
4. D
5. D
6. D
【解析】A.在平行四边形 中,,故A结论正确.
B.在平行四边形 中,,
,
,
,
,
,故B结论正确.
C.在平行四边形 中,,故C结论正确.
D.在平行四边形 中,,
,故D结论不一定成立.故选D.
7. D
8. C
【解析】因为平行四边形的对角线互相平分,
所以 ,,则 与 是等底同高的三角形,
所以 与 的面积相等,
同理, 与 的面积相等.
因此 ,,, 的面积都相等,
所以 .
9. C
10. A
【解析】连接 ,过 作 于 ,交 于 ,过 作 于 ,交 于 ,
,
,
,
,
,
阴影部分面积 ,
阴影部分面积不变.
11. C
【解析】同底等高的三角形的面积相等.
12. D
【解析】 四边形 是平行四边形,
,
,,
,
四边形 是平行四边形,
,,
,
,
.
13. B
【解析】平行线间的距离为平行线上一点到另一条平行线的垂线段的长度.
故选B.
14. B
15. A
【解析】由题图可得,,
又因为 ,
所以线段 的长度是直线 与直线 之间的距离,故选A.
16. A
【解析】选项B是轴对称图形不是中心对称图形,选项C是中心对称图形不是轴对称图形,选项D既不是轴对称图形又不是中心对称图形.故选A.
17. D
18. B
二
19.
20.
21. (或 )
22.
【解析】 四边形 是平行四边形,,
,,
点 的坐标为 ,
点 的坐标为 .
23.
【解析】 平行四边形 的面积为 ,
24. ②⑤
25. ,平行四边形 ,平行四边形 ,平行四边形
26.
【解析】 平行四边形 的对角线 与 相交于点 ,
,,
,
.
三
27. 连接 交 于点 ,
则 ,,
.
28. 过点 作 于点 .
经测量可得:,,则 与 之间的距离是 , 与 之间的距离是 .
29. 连接 .
由图形可知:,
即 .
,
,
.
30. 如图所示(答案不唯一).
31. ,
.
在 和 中,
,
,
是等腰三角形.
平分 ,
.
