8.1.2棱锥 能力冲刺(含解析)
文档属性
| 名称 | 8.1.2棱锥 能力冲刺(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-07 07:25:23 | ||
图片预览




文档简介
第八章8.1.2棱锥能力冲刺--人教A版(2019)必修第二册
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,正四棱锥,M,N为棱PA,PC的中点,平面BMN与棱PD交于点Q,则下列说法正确的是( )
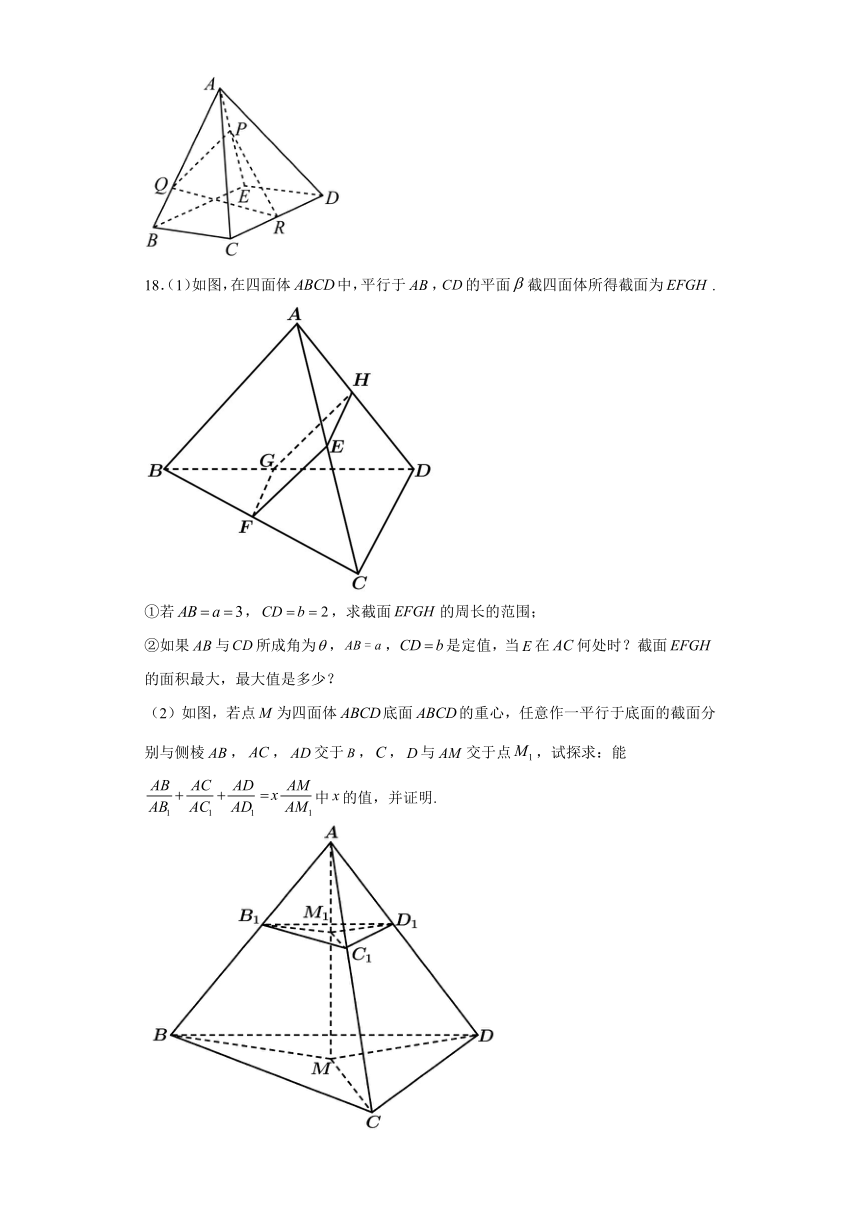
A.四边形MBNQ是菱形
B.四边形MBNQ对角线MN中点也是四棱锥高线的中点
C.
D.
2.三棱锥中,,若三角形和都是等腰直角三角形,则可能的不同取值有( )
A.1种 B.2种 C.3种 D.至少4种
3.一个四棱锥的底面为正方形,且底面边长与各侧棱长相等,另一个三棱锥的底面边长与各侧棱长也都相等,这两个棱锥恰好可以拼接成一个三棱柱.设四棱锥、三棱锥、三棱柱的高分别为、、,则( )
A. B.
C. D.
4.一个四棱锥和一个三棱锥恰好可以拼接成一个三棱柱,这个四棱锥的底面为正方形,且底面边长与各侧棱长相等,这个三棱锥的底面边长与各侧棱长也都相等.设四棱锥、三棱锥、三棱柱的高分别为、、,则( )
A. B. C. D.
5.1859年,英国作家约翰·泰勒(John Taylor,1781-1846)在其《大金字塔》一书中提出:古埃及人在建造胡夫金字塔时利用了黄金数().泰勒还引用了古希腊历史学家希罗多德的记载:胡夫金字塔的形状为正四棱锥,每一个侧面的面积都等于金字塔高的平方.如图,已知金字塔型正四棱锥的底面边长约为656英尺,顶点P在底面上的投影为底面的中心O,H为线段BC的中点,根据以上信息,的长度(单位:英尺)约为( )
A.302.7 B.405.4 C.530.7 D.1061.4
6.北京大兴国际机场的显著特点之一是各种弯曲空间的运用.刻画空间的弯曲性是几何研究的重要内容.用曲率刻画空间弯曲性,规定:多面体顶点的曲率等于与多面体在该点的面角之和的差(多面体的面的内角叫做多面体的面角,角度用弧度制),多面体面上非顶点的曲率均为零,多面体的总曲率等于该多面体各顶点的曲率之和,例如:正四面体在每个顶点有3个面角,每个面角是,所以正四面体在各顶点的曲率为,故其总曲率为,则四棱锥的总曲率为( )
A. B. C. D.
7.以下关于正棱锥的叙述不正确的是( )
A.正棱锥的高与底面的交点是底面的中心
B.正四棱锥的各侧面都是锐角三角形
C.正棱锥的各侧面都是等腰三角形
D.底面是正多边形且各侧面都是等腰三角形的棱锥是正棱锥
8.在四面体中,,与直线,均垂直,且,一只蚂蚁从的中心沿表面爬至点,则其爬过的路程最小值为( )
A. B. C. D.
二、多选题
9.如图,以等腰直角三角形斜边上的高为折痕,把和折成互相垂直的两个平面后,某学生得出下列四个结论,其中正确的是( )
A.;
B.;
C.三棱锥是正三棱锥;
D.平面的法向量和平面的法向量互相垂直.
10.(多选)在正方体的8个顶点中任意取4个不同的顶点,则这4个顶点可能构成( )
A.矩形
B.每个面都是等边三角形的四面体
C.每个面都是直角三角形的四面体
D.有三个面是直角三角形、一个面是等边三角形的四面体
11.某人用如图所示的纸片沿折痕折后粘成一个四棱锥形的“走马灯”,正方形做灯底,且有一个三角形面上写上了“年”字,当灯旋转时,正好看到“新年快乐”的字样,则在①、②、③处应依次写上( )
A.乐、新、快 B.快、新、乐
C.新、快、乐 D.乐、快、新
12.下列说法正确的是( )
A.四棱柱的所有面均为平行四边形
B.长方体不一定是正四棱柱
C.底面是正多边形的棱锥,是正棱锥
D.正四面体一定是正三棱锥
三、填空题
13.设P为多面体M的一个顶点,定义多面体M在点P处的离散曲率为:,其中为多面体M的所有与点P相邻的顶点,且平面,平面,,平面和平面遍历多面体M的所有以点P为公共点的面,在长方体中,,,点S为底面的中心,记三棱锥在点A处的离散曲率为,四棱锥在点S处的离散曲率为n,则________.
14.已知正三棱锥满足,,则______.
15.已知正三棱锥P—ABC的侧面是顶角为,腰长为2的等腰三角形,若过A的截面与棱PB、PC分别交于点D、E,则截面△AED周长的最小值为______.
16.如图,正四面体的棱长为1,棱平面,则正四面体上的所有点在平面内的射影构成的图形面积的最小值是___________.
四、解答题
17.(1)如图,棱长为2的正方体中,,是棱,的中点,在图中画出过底面中的心且与平面平行的平面在正方体中的截面,并求出截面多边形的周长为:______;
(2)作出平面与四棱锥的截面,截面多边形的边数为______.
18.(1)如图,在四面体中,平行于,的平面截四面体所得截面为.
①若,,求截面的周长的范围;
②如果与所成角为,,是定值,当在何处时?截面的面积最大,最大值是多少?
(2)如图,若点为四面体底面的重心,任意作一平行于底面的截面分别与侧棱,,交于,,与交于点,试探求:能中的值,并证明.
参考答案:
1.B
【分析】如图连接,、,设,连接,设,即可得到,从而判断B正确,延长交于点,连接、,即可判断为上靠近的三等分点,从而得到A、C错误,因为侧棱与底面边长关系无法确定,从而无法判断;
【详解】解:如图连接,、,设,连接,设,
因为M,N为棱PA,PC的中点,所以,则为的中点,根据正四棱锥的性质可知即为四棱锥的高,故B正确;
延长交于点,连接、,则,
因为、、三点共线,所以,即,所以为上靠近的三等分点,
显然,但是,故四边形不是菱形,且与不相似,故A、C错误;
因为正四棱锥的侧棱与底面边长关系无法得知,故无法确定,故D错误;
故选:B
2.C
【分析】对三角形和三角形的各边位置关系进行分类讨论,求解出不同情况下的取值,进而得出所有可能取值的种数.
【详解】根据题意可画简图如下,为等边三角形,且都是等腰直角三角形,分类讨论如下:
时, ,此时中,
所以,
此时,
时,,此时中,
,此时,此时;
时,,此时中,
,此时,此时
所以的取值有3种不同情况.
故选:C.
3.B
【分析】根据题意,画出相应的直观图即可求出相应的高即其比值.
【详解】如图,
设正三棱锥的边长为,则四棱锥的边长也为,点为四棱锥底面中心,点为的中点,为底面三角形的中心也为点在底面的投影,
解得,
,于是,
因为为底面三角形的中心,所以
所以
所以.
故选:B
4.C
【分析】由题设易知,设利用正方形、正三角形的性质及勾股定理求出、、,即可知它们的比例关系.
【详解】设四棱锥为,三棱锥为,则三棱锥为正四面体,四棱锥为正四棱锥,显然.
设,正方形的中心为,正三角形的中心为,
连接,,,,则,,
,,即,,
.
故选:C
5.C
【分析】结合已知条件,利用勾股定理列方程,化简求得的长度.
【详解】设,,,由已知得,
又由勾股定理,故,即,
因此可求得,则.
故选:C
6.B
【分析】根据题中给出的定义,由多面体的总曲率计算求解即可.
【详解】解:由题意,四棱锥的总曲率等于四棱锥各顶点的曲率之和,
因为四棱锥有5个顶点,5个面,其中4个三角形,1个四边形,
所以四棱锥的表面内角和由4个三角形和1个四边形组成,
所以面角和为,
故总曲率为.
故选:B.
7.D
【分析】利用正棱锥的几何性质可判断各选项的正误.
【详解】对于A选项,正棱锥的高与底面的交点是底面的中心,A对;
对于B选项,在正四棱锥中,设点在底面的射影点为点,如下图所示:
设,,则,,
,则为锐角,
易知等腰三角形中,,、均为锐角,即为锐角三角形,B对;
对于C选项,因为正棱锥的侧棱长相等,故正棱锥的各侧面都是等腰三角形,C对;
对于D选项,在三棱锥中,是边长为的等边三角形,,,
则三棱锥的底面是等边三角形,且每个侧面均为等腰三角形,但该三棱锥不是正棱锥,D错.
故选:D.
8.A
【分析】利用垂直条件证明得平面,即可得平面平面,然后根据平面展开图判断最短距离,再利用勾股定理计算求解即可.
【详解】因为,,所以平面,所以平面平面,将底面旋转,以为轴,旋转至平面与平面共面,如图,此时的直线距离即为最短距离,设到直线的距离为,则,所以.
故选:A
9.BC
【分析】通过线面垂直的判定得出平面ADC,进而,故而可判断A;通过证明是等边三角形可判断B;通过正三棱锥的定义可判断C;通过平面和平面不垂直可判断D.
【详解】∵D为BC的中点,∴,
又平面平面ACD,平面平面ACD=AD,
,平面ABD,
∴平面ADC,又平面ADC,
∴,即,故A不正确;
由A知,平面ADC,平面ADC,
∴,设,则,
∴由勾股定理得:,∴是等边三角形,故B正确;
∵是等边三角形,,
∴三棱锥是正三棱锥,故C正确;
由A知,平面ADC,而面内不存在与平行的直线,
故平面和平面不垂直,
即平面的法向量和平面的法向量互相垂直错误;故D错误;
故选:BC.
【点睛】本题主要考查折叠前后线线,线面,面面关系的不变和改变,解题时要前后对应,仔细论证,属于中档题.
10.ABCD
【分析】通过举例判断即可.
【详解】对于A,如图四边形为矩形,所以A正确,
对于B,四面体的每个面都是等边三角形,所以B正确,
对于C,如图四面体的每个面都是直角三角形,所以C正确,
对于D,如图四面体的三个面是直角三角形、一个面是等边三角形,所以D正确,
故选:ABCD
11.BC
【分析】由四棱锥的结构特征进行判断即可
【详解】解:由题意,图中四个三角形为四棱锥的侧面,由四棱锥的结构特征,正好看到“新年快乐”的字样的顺序可以是①年②③,②年①③,
即①②③处可依次写上:新、快、乐,或快、新、乐,
故选:BC
12.BD
【分析】利用棱柱以及棱锥的定义,判断选项的正误即可.
【详解】解:四棱柱的上下底面四边形可以是任意四边形,故A不正确;
长方体不一定是正四棱柱,正确,因为长方体的三边可以不相等,所以B正确;
不仅底面是正多边形,并且顶点在底面内的射影是底面中心,才是正棱锥,故C不正确;
正四面体一定是正三棱锥,故D正确.
故选:BD.
【点睛】本题考查棱锥,棱柱的定义的应用,结构特征的判断,是基础题.关键是要准确掌握有关几何体定义.
13.
【分析】根据离散曲率的定义,结合结合体的结构特征,分别求出三棱锥在点A处的离散曲率,四棱锥在点S处的离散曲率n,相减即可求得答案.
【详解】在长方体中, ,
故三棱锥在点A处的离散曲率;
设交于O,连接,,,四边形为正方形,
则 , ,故 ,同理,
四棱锥为正四棱锥,而 ,则四棱锥每个侧面都为正三角形,
所以 ,
故四棱锥在点S处的离散曲率,
故,
故答案为:
14.
【分析】由正三棱锥的性质和已知,可以得出侧面为等腰直角三角形.
【详解】
正三棱锥,所以AB=AC,
又,所以是等腰直角三角形.
所以,也是等腰直角三角形,.
由,所以,
所以.
故答案为:.
15.
【分析】画出正三棱锥的侧面展开图,利用两点之间线段最短得出截面△AED周长的最小时线段的长,再利用勾股定理可求得的值.
【详解】由题意可得此三棱锥的侧面展开图如图所示,
则△AED周长为,由于两点之间线段最短,
所以当位于如图位置时,截面△AED周长的最小,即为的长,
因为,所以,
因为,
所以,
所以截面△AED周长的最小值为,
故答案为:.
16.
【分析】根据正四面体的性质判断投影构成的图形面积的最小时,四面体与面的位置关系,进而求出投影图形的面积.
【详解】根据平面,将平移至面上,
问题化为四面体绕旋转过程中在面上的投影面积最小,
若为中点,连接,且△、△均为等边三角形,则,
又,面,故面,面,
所以,
要使投影构成的图形面积的最小,只需与的中点所成平面与重合,如下图,
此时正四面体在平面上投影为△,而,,
所以最小投影面积为.
故答案为:
17.(1)作图见解析,周长为;(2)作图见解析,边数为五.
【分析】(1)利用面面平行的判定定理作出截面,求得各边长度则可得周长;(2)利用延长找公共点的方法作出截面,可得形状.
【详解】(1)分别取,为棱,的中点,则由中位线性质得到:,所以四边形为平面四边形,
又,,所以四边形为平行四边形,所以,
由,平面,平面,所以平面,同理平面, ,由面面平行的判定定理可得平面平面,所以四边形即为所求截面,且为梯形,
由截面作法可知,所以截面四边形的周长为.
(2)延长的延长线于,连接的延长线于连接于,连接,则五边形即为所求.所以截面多边形的边数为五.
18.(1)①;②为中点,最大值为;(2),证明见解析.
【分析】(1)①利用线面平行的判定与性质,证出且,从而得到四边形
的两组对边分别平行,即四边形为平行四边形.
②根据线面平行的性质定理,容易得到,同理可得,所以得到,
同理可得到截面的另一组对边,这样便得到截面的两组对边都平行,
即得到截面是平行四边形;
(2)利用平面与平面平行的性质,即可得出结论.
【详解】(1)①证明:平面,平面,平面平面
.
同理可得,可得,同理得到,
四边形为平行四边形.
且, ,①,②,
则①②得,,
,
四边形的周长,
,四边形的周长为;
②与所成角为,
平行四边形中或,
为平行四边形,令,
,
,
当时,即为中点时,截面面积最大,最大值为;
(2)当截面无限接近底面时,可得,证明如下:
由题意,任意作一平行于底面的截面分别与侧棱,,交于,,与交
于点,
,,,
,,,
.
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.如图,正四棱锥,M,N为棱PA,PC的中点,平面BMN与棱PD交于点Q,则下列说法正确的是( )
A.四边形MBNQ是菱形
B.四边形MBNQ对角线MN中点也是四棱锥高线的中点
C.
D.
2.三棱锥中,,若三角形和都是等腰直角三角形,则可能的不同取值有( )
A.1种 B.2种 C.3种 D.至少4种
3.一个四棱锥的底面为正方形,且底面边长与各侧棱长相等,另一个三棱锥的底面边长与各侧棱长也都相等,这两个棱锥恰好可以拼接成一个三棱柱.设四棱锥、三棱锥、三棱柱的高分别为、、,则( )
A. B.
C. D.
4.一个四棱锥和一个三棱锥恰好可以拼接成一个三棱柱,这个四棱锥的底面为正方形,且底面边长与各侧棱长相等,这个三棱锥的底面边长与各侧棱长也都相等.设四棱锥、三棱锥、三棱柱的高分别为、、,则( )
A. B. C. D.
5.1859年,英国作家约翰·泰勒(John Taylor,1781-1846)在其《大金字塔》一书中提出:古埃及人在建造胡夫金字塔时利用了黄金数().泰勒还引用了古希腊历史学家希罗多德的记载:胡夫金字塔的形状为正四棱锥,每一个侧面的面积都等于金字塔高的平方.如图,已知金字塔型正四棱锥的底面边长约为656英尺,顶点P在底面上的投影为底面的中心O,H为线段BC的中点,根据以上信息,的长度(单位:英尺)约为( )
A.302.7 B.405.4 C.530.7 D.1061.4
6.北京大兴国际机场的显著特点之一是各种弯曲空间的运用.刻画空间的弯曲性是几何研究的重要内容.用曲率刻画空间弯曲性,规定:多面体顶点的曲率等于与多面体在该点的面角之和的差(多面体的面的内角叫做多面体的面角,角度用弧度制),多面体面上非顶点的曲率均为零,多面体的总曲率等于该多面体各顶点的曲率之和,例如:正四面体在每个顶点有3个面角,每个面角是,所以正四面体在各顶点的曲率为,故其总曲率为,则四棱锥的总曲率为( )
A. B. C. D.
7.以下关于正棱锥的叙述不正确的是( )
A.正棱锥的高与底面的交点是底面的中心
B.正四棱锥的各侧面都是锐角三角形
C.正棱锥的各侧面都是等腰三角形
D.底面是正多边形且各侧面都是等腰三角形的棱锥是正棱锥
8.在四面体中,,与直线,均垂直,且,一只蚂蚁从的中心沿表面爬至点,则其爬过的路程最小值为( )
A. B. C. D.
二、多选题
9.如图,以等腰直角三角形斜边上的高为折痕,把和折成互相垂直的两个平面后,某学生得出下列四个结论,其中正确的是( )
A.;
B.;
C.三棱锥是正三棱锥;
D.平面的法向量和平面的法向量互相垂直.
10.(多选)在正方体的8个顶点中任意取4个不同的顶点,则这4个顶点可能构成( )
A.矩形
B.每个面都是等边三角形的四面体
C.每个面都是直角三角形的四面体
D.有三个面是直角三角形、一个面是等边三角形的四面体
11.某人用如图所示的纸片沿折痕折后粘成一个四棱锥形的“走马灯”,正方形做灯底,且有一个三角形面上写上了“年”字,当灯旋转时,正好看到“新年快乐”的字样,则在①、②、③处应依次写上( )
A.乐、新、快 B.快、新、乐
C.新、快、乐 D.乐、快、新
12.下列说法正确的是( )
A.四棱柱的所有面均为平行四边形
B.长方体不一定是正四棱柱
C.底面是正多边形的棱锥,是正棱锥
D.正四面体一定是正三棱锥
三、填空题
13.设P为多面体M的一个顶点,定义多面体M在点P处的离散曲率为:,其中为多面体M的所有与点P相邻的顶点,且平面,平面,,平面和平面遍历多面体M的所有以点P为公共点的面,在长方体中,,,点S为底面的中心,记三棱锥在点A处的离散曲率为,四棱锥在点S处的离散曲率为n,则________.
14.已知正三棱锥满足,,则______.
15.已知正三棱锥P—ABC的侧面是顶角为,腰长为2的等腰三角形,若过A的截面与棱PB、PC分别交于点D、E,则截面△AED周长的最小值为______.
16.如图,正四面体的棱长为1,棱平面,则正四面体上的所有点在平面内的射影构成的图形面积的最小值是___________.
四、解答题
17.(1)如图,棱长为2的正方体中,,是棱,的中点,在图中画出过底面中的心且与平面平行的平面在正方体中的截面,并求出截面多边形的周长为:______;
(2)作出平面与四棱锥的截面,截面多边形的边数为______.
18.(1)如图,在四面体中,平行于,的平面截四面体所得截面为.
①若,,求截面的周长的范围;
②如果与所成角为,,是定值,当在何处时?截面的面积最大,最大值是多少?
(2)如图,若点为四面体底面的重心,任意作一平行于底面的截面分别与侧棱,,交于,,与交于点,试探求:能中的值,并证明.
参考答案:
1.B
【分析】如图连接,、,设,连接,设,即可得到,从而判断B正确,延长交于点,连接、,即可判断为上靠近的三等分点,从而得到A、C错误,因为侧棱与底面边长关系无法确定,从而无法判断;
【详解】解:如图连接,、,设,连接,设,
因为M,N为棱PA,PC的中点,所以,则为的中点,根据正四棱锥的性质可知即为四棱锥的高,故B正确;
延长交于点,连接、,则,
因为、、三点共线,所以,即,所以为上靠近的三等分点,
显然,但是,故四边形不是菱形,且与不相似,故A、C错误;
因为正四棱锥的侧棱与底面边长关系无法得知,故无法确定,故D错误;
故选:B
2.C
【分析】对三角形和三角形的各边位置关系进行分类讨论,求解出不同情况下的取值,进而得出所有可能取值的种数.
【详解】根据题意可画简图如下,为等边三角形,且都是等腰直角三角形,分类讨论如下:
时, ,此时中,
所以,
此时,
时,,此时中,
,此时,此时;
时,,此时中,
,此时,此时
所以的取值有3种不同情况.
故选:C.
3.B
【分析】根据题意,画出相应的直观图即可求出相应的高即其比值.
【详解】如图,
设正三棱锥的边长为,则四棱锥的边长也为,点为四棱锥底面中心,点为的中点,为底面三角形的中心也为点在底面的投影,
解得,
,于是,
因为为底面三角形的中心,所以
所以
所以.
故选:B
4.C
【分析】由题设易知,设利用正方形、正三角形的性质及勾股定理求出、、,即可知它们的比例关系.
【详解】设四棱锥为,三棱锥为,则三棱锥为正四面体,四棱锥为正四棱锥,显然.
设,正方形的中心为,正三角形的中心为,
连接,,,,则,,
,,即,,
.
故选:C
5.C
【分析】结合已知条件,利用勾股定理列方程,化简求得的长度.
【详解】设,,,由已知得,
又由勾股定理,故,即,
因此可求得,则.
故选:C
6.B
【分析】根据题中给出的定义,由多面体的总曲率计算求解即可.
【详解】解:由题意,四棱锥的总曲率等于四棱锥各顶点的曲率之和,
因为四棱锥有5个顶点,5个面,其中4个三角形,1个四边形,
所以四棱锥的表面内角和由4个三角形和1个四边形组成,
所以面角和为,
故总曲率为.
故选:B.
7.D
【分析】利用正棱锥的几何性质可判断各选项的正误.
【详解】对于A选项,正棱锥的高与底面的交点是底面的中心,A对;
对于B选项,在正四棱锥中,设点在底面的射影点为点,如下图所示:
设,,则,,
,则为锐角,
易知等腰三角形中,,、均为锐角,即为锐角三角形,B对;
对于C选项,因为正棱锥的侧棱长相等,故正棱锥的各侧面都是等腰三角形,C对;
对于D选项,在三棱锥中,是边长为的等边三角形,,,
则三棱锥的底面是等边三角形,且每个侧面均为等腰三角形,但该三棱锥不是正棱锥,D错.
故选:D.
8.A
【分析】利用垂直条件证明得平面,即可得平面平面,然后根据平面展开图判断最短距离,再利用勾股定理计算求解即可.
【详解】因为,,所以平面,所以平面平面,将底面旋转,以为轴,旋转至平面与平面共面,如图,此时的直线距离即为最短距离,设到直线的距离为,则,所以.
故选:A
9.BC
【分析】通过线面垂直的判定得出平面ADC,进而,故而可判断A;通过证明是等边三角形可判断B;通过正三棱锥的定义可判断C;通过平面和平面不垂直可判断D.
【详解】∵D为BC的中点,∴,
又平面平面ACD,平面平面ACD=AD,
,平面ABD,
∴平面ADC,又平面ADC,
∴,即,故A不正确;
由A知,平面ADC,平面ADC,
∴,设,则,
∴由勾股定理得:,∴是等边三角形,故B正确;
∵是等边三角形,,
∴三棱锥是正三棱锥,故C正确;
由A知,平面ADC,而面内不存在与平行的直线,
故平面和平面不垂直,
即平面的法向量和平面的法向量互相垂直错误;故D错误;
故选:BC.
【点睛】本题主要考查折叠前后线线,线面,面面关系的不变和改变,解题时要前后对应,仔细论证,属于中档题.
10.ABCD
【分析】通过举例判断即可.
【详解】对于A,如图四边形为矩形,所以A正确,
对于B,四面体的每个面都是等边三角形,所以B正确,
对于C,如图四面体的每个面都是直角三角形,所以C正确,
对于D,如图四面体的三个面是直角三角形、一个面是等边三角形,所以D正确,
故选:ABCD
11.BC
【分析】由四棱锥的结构特征进行判断即可
【详解】解:由题意,图中四个三角形为四棱锥的侧面,由四棱锥的结构特征,正好看到“新年快乐”的字样的顺序可以是①年②③,②年①③,
即①②③处可依次写上:新、快、乐,或快、新、乐,
故选:BC
12.BD
【分析】利用棱柱以及棱锥的定义,判断选项的正误即可.
【详解】解:四棱柱的上下底面四边形可以是任意四边形,故A不正确;
长方体不一定是正四棱柱,正确,因为长方体的三边可以不相等,所以B正确;
不仅底面是正多边形,并且顶点在底面内的射影是底面中心,才是正棱锥,故C不正确;
正四面体一定是正三棱锥,故D正确.
故选:BD.
【点睛】本题考查棱锥,棱柱的定义的应用,结构特征的判断,是基础题.关键是要准确掌握有关几何体定义.
13.
【分析】根据离散曲率的定义,结合结合体的结构特征,分别求出三棱锥在点A处的离散曲率,四棱锥在点S处的离散曲率n,相减即可求得答案.
【详解】在长方体中, ,
故三棱锥在点A处的离散曲率;
设交于O,连接,,,四边形为正方形,
则 , ,故 ,同理,
四棱锥为正四棱锥,而 ,则四棱锥每个侧面都为正三角形,
所以 ,
故四棱锥在点S处的离散曲率,
故,
故答案为:
14.
【分析】由正三棱锥的性质和已知,可以得出侧面为等腰直角三角形.
【详解】
正三棱锥,所以AB=AC,
又,所以是等腰直角三角形.
所以,也是等腰直角三角形,.
由,所以,
所以.
故答案为:.
15.
【分析】画出正三棱锥的侧面展开图,利用两点之间线段最短得出截面△AED周长的最小时线段的长,再利用勾股定理可求得的值.
【详解】由题意可得此三棱锥的侧面展开图如图所示,
则△AED周长为,由于两点之间线段最短,
所以当位于如图位置时,截面△AED周长的最小,即为的长,
因为,所以,
因为,
所以,
所以截面△AED周长的最小值为,
故答案为:.
16.
【分析】根据正四面体的性质判断投影构成的图形面积的最小时,四面体与面的位置关系,进而求出投影图形的面积.
【详解】根据平面,将平移至面上,
问题化为四面体绕旋转过程中在面上的投影面积最小,
若为中点,连接,且△、△均为等边三角形,则,
又,面,故面,面,
所以,
要使投影构成的图形面积的最小,只需与的中点所成平面与重合,如下图,
此时正四面体在平面上投影为△,而,,
所以最小投影面积为.
故答案为:
17.(1)作图见解析,周长为;(2)作图见解析,边数为五.
【分析】(1)利用面面平行的判定定理作出截面,求得各边长度则可得周长;(2)利用延长找公共点的方法作出截面,可得形状.
【详解】(1)分别取,为棱,的中点,则由中位线性质得到:,所以四边形为平面四边形,
又,,所以四边形为平行四边形,所以,
由,平面,平面,所以平面,同理平面, ,由面面平行的判定定理可得平面平面,所以四边形即为所求截面,且为梯形,
由截面作法可知,所以截面四边形的周长为.
(2)延长的延长线于,连接的延长线于连接于,连接,则五边形即为所求.所以截面多边形的边数为五.
18.(1)①;②为中点,最大值为;(2),证明见解析.
【分析】(1)①利用线面平行的判定与性质,证出且,从而得到四边形
的两组对边分别平行,即四边形为平行四边形.
②根据线面平行的性质定理,容易得到,同理可得,所以得到,
同理可得到截面的另一组对边,这样便得到截面的两组对边都平行,
即得到截面是平行四边形;
(2)利用平面与平面平行的性质,即可得出结论.
【详解】(1)①证明:平面,平面,平面平面
.
同理可得,可得,同理得到,
四边形为平行四边形.
且, ,①,②,
则①②得,,
,
四边形的周长,
,四边形的周长为;
②与所成角为,
平行四边形中或,
为平行四边形,令,
,
,
当时,即为中点时,截面面积最大,最大值为;
(2)当截面无限接近底面时,可得,证明如下:
由题意,任意作一平行于底面的截面分别与侧棱,,交于,,与交
于点,
,,,
,,,
.
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
