8.1.1棱柱 能力冲刺练习(含解析)
文档属性
| 名称 | 8.1.1棱柱 能力冲刺练习(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-07 07:25:50 | ||
图片预览



文档简介
第八章8.1.1棱柱能力冲刺--人教A版(2019)必修第二册
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.用一个平面截正方体,截面图形可能是( )
A.钝角三角形 B.直角梯形
C.有两个内角相等的五边形 D.正七边形
2.在正方体中,棱长为4,、分别为棱、的中点,点在对角线上,且,过点、、作一个截面,该截面的形状为( )
A.三角形 B.四边形 C.五边形 D.六边形
3.一个棱长为1的正方体容器,在八个顶点处分别有一个出口(出口大小忽略不计).现从A点放入一个粒子.粒子沿着直线运动,碰到容器壁会进行反射(遵循反射定律),遇到出口就会飞出容器.已知粒子在飞出容器前与容器壁产生了三次碰撞(粒子未与棱产生碰撞),则粒子在容器内的飞行距离有( )种不同的值
A.1 B.2 C.3 D.4
4.、两个动点从棱长为的正方体的顶点出发沿棱向前运动.动点运动的路线是,运动规则如下:第段与第段(其中是正整数)所在直线一定是异面直线.动点运动的路线是,它和点具有相同的运动规则.那么动点运动完段、动点运动完段后各自停止在正方体的某个顶点处,此时动点、的距离是( )
A. B. C. D.
5.已知直三棱柱中,,,为线段上的动点,则的最小值为( )
A. B. C. D.
6.在正方体中,棱长为4,为的中点,点在平面内运动,则的最小值为( )
A.6 B. C. D.10
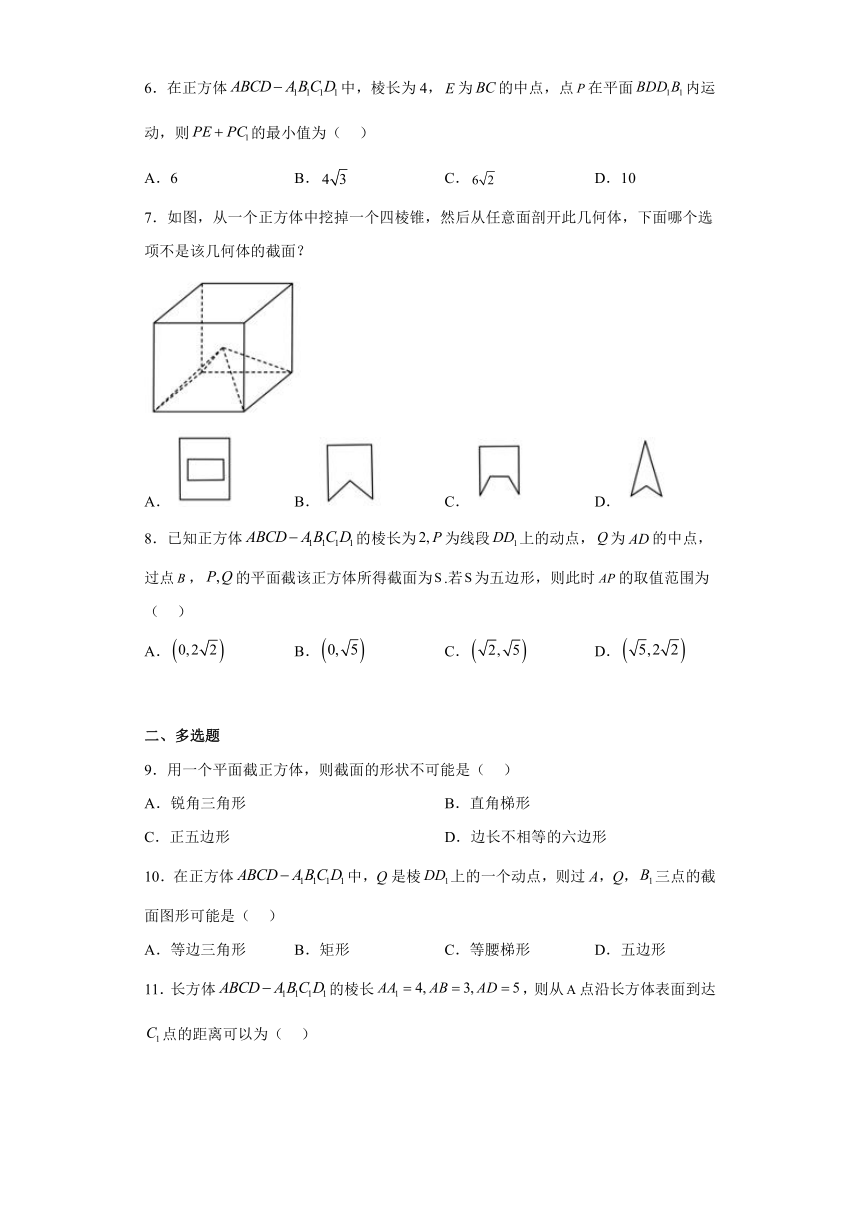
7.如图,从一个正方体中挖掉一个四棱锥,然后从任意面剖开此几何体,下面哪个选项不是该几何体的截面?
A. B. C. D.
8.已知正方体的棱长为为线段上的动点,为的中点,过点,的平面截该正方体所得截面为.若为五边形,则此时的取值范围为( )
A. B. C. D.
二、多选题
9.用一个平面截正方体,则截面的形状不可能是( )
A.锐角三角形 B.直角梯形
C.正五边形 D.边长不相等的六边形
10.在正方体中,Q是棱上的一个动点,则过A,Q,三点的截面图形可能是( )
A.等边三角形 B.矩形 C.等腰梯形 D.五边形
11.长方体的棱长,则从点沿长方体表面到达点的距离可以为( )
A. B. C. D.
12.在正方体中,如图M,N分别是正方形,的中心.则下列结论正确的是( )
A.平面与棱的交点是的三等分点
B.平面与棱的交点是的中点
C.平面与棱的交点是的三等分点
D.平面将正方体分成前后两部分的体积比为
三、填空题
13.如图,已知正三棱柱的底面边长为1cm,高为5cm,一质点自点出发,沿着三棱柱的侧面绕行两周到达点的最短路线的长为___________.
14.在一个的长方体黑盒内,每个面的内壁都装有平面镜,八个角均凿了小孔,一束激光从某个孔射入,入射光线与该孔所对应的三条棱的夹角均彼此相同,则该束光线经过______次反射后穿出盒外.
15.如图,在棱长为的正方体中,分别为棱的中点,若点分别为线段上的动点,则的最小值为 _____.
16.正方体的棱长为,设为中点,为线段上的动点,,过点,,的平面截该正方体所得截面记为以下结论正确的有___________填上所有正确的说法的序号
①不可能是菱形;
②可能是五边形;
③时,的面积为;
④时,将棱截成长度比为的两部分.
四、解答题
17.对于精美的礼物,通常人们会用包装纸把礼物包好,还会用彩带捆扎包装好的礼物,有时还会扎出一个花结.这些包装彩带也不便宜,因此在捆扎时不仅要考虑美观 结实,也要考虑尽量地节省包装彩带.以长方体的礼物为例,较为典型的两种捆扎方式分别为“十字”和“对角”,如下图所示.
“十字”捆扎 “对角”捆扎
假设1:将礼物视作一个长方体,其长为4,宽为2 高为1;假设2:不考虑花结处的彩带,将每一段彩带视为线段,且完全位于礼物的表面上;假设3:“十字”捆扎中,长方体表面上的每一段彩带(上底面和下底面各2段,每个侧面各1段)都与其相交的棱垂直;假设4:“对角”捆扎中,以某种方式展开长方体后,长方体表面上的每一段彩带(上底面和下底面各2段,每个侧面各1段)在其表面展开图上均落在同一条直线上.
(1)求“十字”捆扎中彩带的总长度;
(2)根据假设4绘制示意图,求“对角”捆扎中彩带的总长度,并比较两种捆扎方式,给出用彩带捆扎礼物的建议.
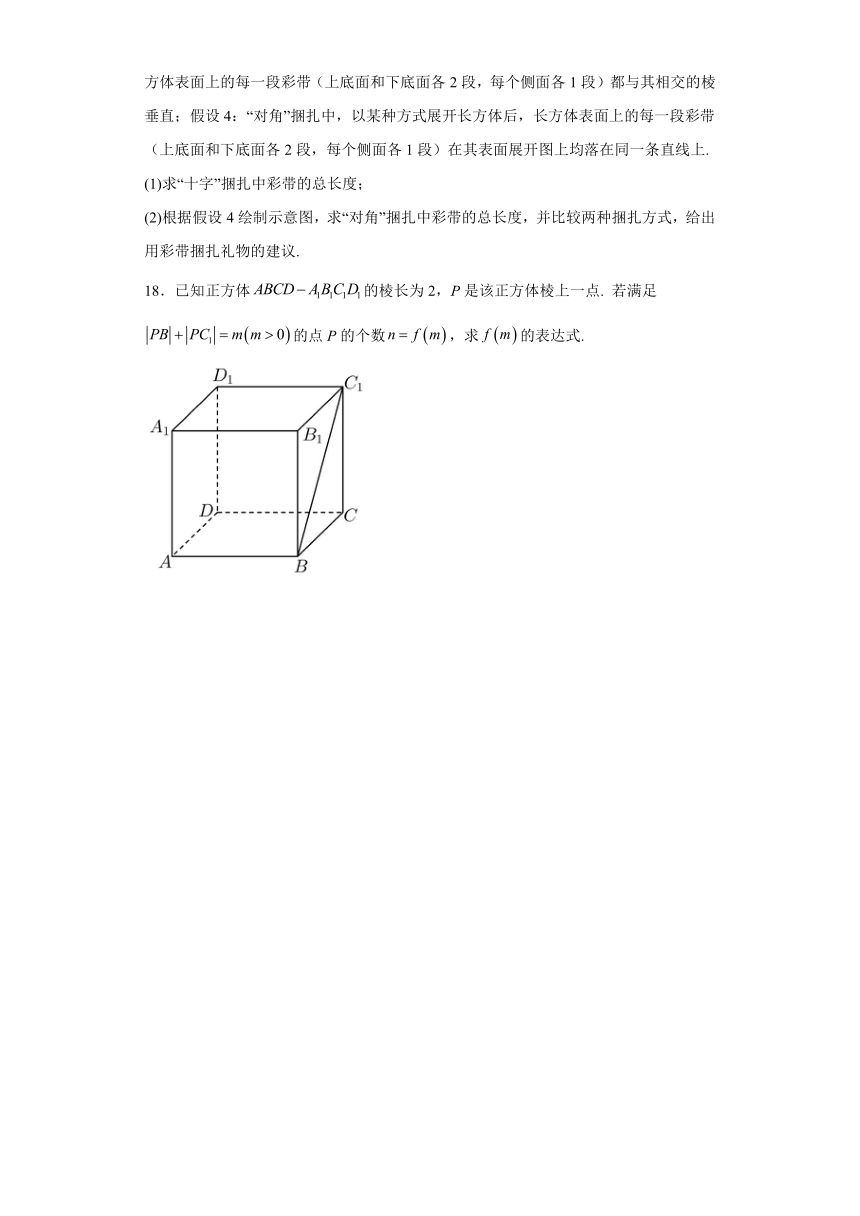
18.已知正方体的棱长为2,P是该正方体棱上一点. 若满足的点P的个数,求的表达式.
参考答案:
1.C
【分析】根据正方体的截面分析得到答案.
【详解】用一个平面截正方体,截面图形可能是三角形,四边形,五边形,六边形.
对于A:截面图形如果是三角形,只能是锐角三角形,不可能是直角三角形和钝角三角形.
如图所示的截面三角形.
设,所以,,.
所以由余弦定理得:所以为锐角.
同理可求:为锐角,为锐角.
所以为锐角三角形.故A错误;
对于B:截面图形如果是四边形,可能是正方形,可能是矩形,可能是菱形,可能是一般梯形,也可能是等腰梯形,不可能是直角梯形.
故B错误;
对于C:如图示的截面图为五边形,并且有两个角相等.
故C正确;
对于D:因为正方体有六个面,所以一个平面截正方体,边数最多为6.所以D错误.
故选:C
2.C
【分析】延长,分别交与的延长线于,可得截面过、、,再根据直线与面面相交的性质,分别确定截面与各棱的交点位置,进而确定截面的形状即可.
【详解】因为,故为的中点.又为正方体,故可延长,分别交与的延长线于,设直线分别交于,易得过点、、的面即平面.
因为为中点,且,故,,,所以,故,即.又,故.又为的中点,同理可得,故,所以,,故在线段内.
连接交于,综上可知点、、截正方体的截面为五边形.
故选:C
3.C
【分析】利用正方体的对称性,根据粒子碰撞次数可分别讨论在轴方向上的运动距离,进而判断各情况粒子在容器内的飞行距离,即可得结果.
【详解】因为不能与棱相碰,所以粒子在x,y,z每个方向上的运动路程都不会为0,否则就会在面上运动,必然与棱相碰. 其次,只看x方向上运动(y , z方向同理,因为正方形有对称性),
如果碰撞0次,那么就是运动了1,如果碰撞1次,就是运动了2,以此类推,在x方向上碰撞了n次最后出射的时候在该方向的运动距离就是(n+1),相当于多运动了n. 题目中经过3次碰撞,可以先从碰撞0次入手,3个方向上的位移就是1,1,1(不能与棱相碰),现在碰撞3次,也就是在某个方向上要加距离,每次碰撞则加1:(1)在同一个方向碰撞3次,即距离分别是4,1,1(1,4,1或者1,1,4),结果是. (2)在一个方向碰撞2次,另外一个方向碰撞一次,即3,2,1(2,3,1或1,2,3),结果是根号. (3)在三个方向各碰撞1次,即距离分别是2,2,2,结果是.
综上,粒子飞行距离有三种结果. 这三种情况都可以举出实际例子∶4,1,1,可以看做从A入射,C处射出;3,2,1可以看做从A入射,D处射出;2,2,2可以看做从A入射,B处射出.
故选:C
4.C
【分析】分析可知点、运动的路线呈现周期性变化,且以段为一个周期,确定动点运动完段后、动点运动完段后,这两个动点的位置,即可求得动点、的距离.
【详解】点运动的路线为,
点运动的路线为,
由上可知,点、运动的路线呈现周期性变化,且以段为一个周期,
因为,,
所以,动点运动完段后与点重合,动点运动完段与点重合,
此时,动点、的距离是.
故选:C.
5.D
【分析】利用空间几何体的特征,将沿折起到的位置.使得平面与平面共面,然后两点之间线段最短,再利用余弦定理即可得到答案.
【详解】将沿折起到的位置.使得平面与平面共面,当为线段与的交点时,最小,即最小,则有,
又,所以易得与均为等腰直角三角形,
,
利用余弦定理可知最小值为.
故选:D.
6.A
【分析】作点关于平面的对称点,将点与同侧点距离之和问题转化为相对点距离问题即可.
【详解】如图作点关于的对称点,
,则的最小值为,根据题中数据可知
故选:A
7.A
【分析】可通过确定截面的不同位置去剖开正方体,想象相对应的截面形状,即可确定答案.
【详解】对于A,由于截面中间是矩形,如果可能的话,一定是用和正方体底面平行的截面去剖开
正方体并且是从挖去四棱锥的那部分剖开,但此时剖面中间应该是一个正方形,
因此A图形不可能是截面;
对于B,当从正方体底面的一组相对棱的中点处剖开时,截面正好通过四棱锥顶点,
如图:
此时截面形状如B图形,故B可能是该几何体的截面;
对于C,当截面不经过底面一组相对棱的中点处,并和另一组棱平行去剖开正方体时,
如图中截面PDGH位置:
截面就会如C图形,故C可能是该几何体的截面;
对于D,如图示,按图中截面 的位置去剖开正方体,截面就会如D图形,
故D可能是该几何体的截面;
故答案为:A
8.D
【分析】由题意作出满足条件的图形,由线面位置关系找出截面即可求解
【详解】(1)当即与重合时,过点,,的截面为正方形,不合题设
(2)当,即为中点时,,,则,
所以过点,,的截面为梯形,不合题设
(3)当即与重合时,取中点,中点,连接,,,
因为,所以四边形为平行四边形,所以
因为,所以四边形为平行四边形,所以
所以
所以过点,,的截面为平行四边形,不合题设
(4)当时,过作交线段于,过作交线段于,连接
因为,所以四边形为平行四边形,所以
又,所以
所以过点,,的截面为梯形,不合题设
(5)当时,取中点,在线段上截取,连接,,过作交线段的延长线于点,交线段于点,连接交于点,连接
因为,所以四边形为平行四边形,所以
又,所以
所以过点,,的截面为五边形,符合题设
此时,,
所以的取值范围为
故选:D
9.BC
【分析】根据正方体的截面特点,对四个选项一一判断.
【详解】对于A:截面图形如果是三角形,只能是锐角三角形,不可能是直角三角形和钝角三角形.
如图所示的截面三角形.
设,所以,,.
所以由余弦定理得:所以为锐角.
同理可求:为锐角,为锐角.
所以为锐角三角形.故A不选.
对于B:截面图形如果是四边形,可能是正方形,可能是矩形,可能是菱形,可能是一般梯形,也可能是等腰梯形,不可能是直角梯形.
B选
对于C:当截面为五边形时,不可能出现正五边形.
C选.
对于D:如果截面经过各个棱的中点,得到的是正六边形,如果与各个棱相交,但不全经过各个棱的中点,得到的是边长不全相等的六边形,故D不选.
故选:BC.
10.ABC
【分析】对于A,当点Q与点重合时判断截面形状,对于B,当点Q与点D重合时判断截面形状,对于C,当点Q不与点D,重合时,延长交延长线于,连接交于,连接,可得截面为梯形,当为的中点时进行判断,对于D,由选项ABC判断.
【详解】对于A,当点Q与点重合时,截面图形为等边三角形,所以A正确;
对于B,当点Q与点D重合时,截面图形为矩形,所以B正确;
对于C,当点Q不与点D,重合时,如图,延长交延长线于,连接交于,连接,因为平面∥平面,平面平面,平面 ,所以∥,所以过A,Q,三点的截面为梯形,当为的中点时,可得,所以,所以为的中点,所以,所以此时梯形为等腰梯形,所以C正确,
对于D,由选项ABC,可知截面图形不可能为五边形,
故选:ABC
11.ABC
【分析】从点沿长方体表面到达有三种展开方式,以、、为轴展开,分别求可得答案.
【详解】则从点沿长方体表面到达有三种展开方式,
若以为轴展开,则,
若以为轴展开,则,
若以为轴展开,则.
故选:ABC.
12.ACD
【分析】由公理作出平面与正方体的截面,利用平行线截线段成比例可得点是线段靠近点的三等分点,由对称性知点是线段靠近点的三等分点,
点是线段靠近点的三等分点;再利用等体积法可知,得到平面将正方体分成两部分的体积比为,即可得解.
【详解】解:如图,取的中点,延长,并交于点,连接并延长,设,,
连接并延长交于点,连接,,则四边形就是平面与正方体的截面,
是平面的中心,是中点,,则,
可得点是线段靠近点的三等分点,由对称性知点是线段靠近点的三等分点,
点是线段靠近点的三等分点,故A正确,B错误,C正确;
作出线段的另一个三等分点,作出线段靠近的三等分点,连接,,,,
可知.
,
从而平面将正方体分成两部分的体积比为,
故D正确.
故选:ACD.
13.
【分析】曲面最值问题一般都化曲为平,变成两点间线段最短.
【详解】
如图将正三棱柱侧面展开2次,可知曲面上的最小值即为对角线=
故答案为:
14.21
【分析】作出空间直角坐标系,得出三个坐标轴坐标的变化规律,得出光束的路径,进而求出光反射的次数.
【详解】解:由题意,
在的长方体中,
入射光线与该孔所对应的三条棱的夹角均彼此相同
∴沿对角线入射,
∴各坐标变化规律如下:
建立空间直角坐标系如下图所示:
假设光线从点射入,则光线路径如下:
根据光线路径可知,共经过了21次反射.
∴该束光线经过了21次反射.
故答案为:21.
15.
【分析】由可确定为中点时,最小,取,通过三角形全等可将问题转化为最小值的求解问题,根据三点共线时线段和最小可求得结果.
【详解】
,当为中点时,取得最小值;
在上取一点,使得,
,,,
;
则当三点共线时,最小,即最小,
此时且,的最小值为.
故答案为:.
16.②③④
【分析】对四个说法逐一分析,画出截面,结合线线平行、点共面等知识确定正确答案.
【详解】①当时,与重合,取的中点,连接,
根据正方体的性质可知,且,
所以截面为菱形,
故①错误;
对于②④,当时,
延长,交的延长线于,连接并延长,交于,
设,连接,
由于,结合正方体的性质可知,
结合共面可知为截面,
如图所示,
点是的中点,可得,,
与的交点满足,此时是五边形,且将棱截成长度比为的两部分.
故②④正确;
对于③,当时,根据正方体的性质可知,且,
如图所示,为等腰梯形,
可得,,等腰梯形得高为,
则的面积为.
故③正确.
故答案为:②③④
17.(1)
(2),在实际生活中包装彩带时应选择“对角”捆扎的方式,更节省包装彩带
【分析】(1)直接利用题意即可求出采用“十字”捆扎中彩带的总长度;(2)求出“对角”捆扎中彩带的总长度,比较大小,即可得到答案.
【详解】(1)采用“十字”捆扎中彩带的总长度为;
(2)
由于,因此在实际生活中包装彩带时应选择“对角”捆扎的方式,更节省包装彩带.
18.
【分析】由几何直观,点P所在的位置与的值一一对应,根据正方体的对称性,分别讨论点P在:(1)棱、、、;(2)棱、;(3) 棱、;(4)棱、、、时的可能取值,即可汇总得P的个数及对应m的范围.
【详解】由题,由几何直观可知,点P在正方体的每一条棱上运动时,它所在的位置与的值是一一对应的,先讨论的可能取值:
(1)当点P分别在棱、、、上运动时,如在棱,可得
,其它同理,故此时m的取值范围是;
(2)当点P分别棱、上运动时,如在棱,可得
,其它同理,故此时m的取值范围是;
(3)当点P分别在棱、上运动时,如在棱,可得
,其它同理,故此时m的取值范围是;
(4)当点P分别在棱、、、上运动时,如在棱,可得
,其它同理,故此时m的取值范围是.
综上,点P的个数为可归结为:
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.用一个平面截正方体,截面图形可能是( )
A.钝角三角形 B.直角梯形
C.有两个内角相等的五边形 D.正七边形
2.在正方体中,棱长为4,、分别为棱、的中点,点在对角线上,且,过点、、作一个截面,该截面的形状为( )
A.三角形 B.四边形 C.五边形 D.六边形
3.一个棱长为1的正方体容器,在八个顶点处分别有一个出口(出口大小忽略不计).现从A点放入一个粒子.粒子沿着直线运动,碰到容器壁会进行反射(遵循反射定律),遇到出口就会飞出容器.已知粒子在飞出容器前与容器壁产生了三次碰撞(粒子未与棱产生碰撞),则粒子在容器内的飞行距离有( )种不同的值
A.1 B.2 C.3 D.4
4.、两个动点从棱长为的正方体的顶点出发沿棱向前运动.动点运动的路线是,运动规则如下:第段与第段(其中是正整数)所在直线一定是异面直线.动点运动的路线是,它和点具有相同的运动规则.那么动点运动完段、动点运动完段后各自停止在正方体的某个顶点处,此时动点、的距离是( )
A. B. C. D.
5.已知直三棱柱中,,,为线段上的动点,则的最小值为( )
A. B. C. D.
6.在正方体中,棱长为4,为的中点,点在平面内运动,则的最小值为( )
A.6 B. C. D.10
7.如图,从一个正方体中挖掉一个四棱锥,然后从任意面剖开此几何体,下面哪个选项不是该几何体的截面?
A. B. C. D.
8.已知正方体的棱长为为线段上的动点,为的中点,过点,的平面截该正方体所得截面为.若为五边形,则此时的取值范围为( )
A. B. C. D.
二、多选题
9.用一个平面截正方体,则截面的形状不可能是( )
A.锐角三角形 B.直角梯形
C.正五边形 D.边长不相等的六边形
10.在正方体中,Q是棱上的一个动点,则过A,Q,三点的截面图形可能是( )
A.等边三角形 B.矩形 C.等腰梯形 D.五边形
11.长方体的棱长,则从点沿长方体表面到达点的距离可以为( )
A. B. C. D.
12.在正方体中,如图M,N分别是正方形,的中心.则下列结论正确的是( )
A.平面与棱的交点是的三等分点
B.平面与棱的交点是的中点
C.平面与棱的交点是的三等分点
D.平面将正方体分成前后两部分的体积比为
三、填空题
13.如图,已知正三棱柱的底面边长为1cm,高为5cm,一质点自点出发,沿着三棱柱的侧面绕行两周到达点的最短路线的长为___________.
14.在一个的长方体黑盒内,每个面的内壁都装有平面镜,八个角均凿了小孔,一束激光从某个孔射入,入射光线与该孔所对应的三条棱的夹角均彼此相同,则该束光线经过______次反射后穿出盒外.
15.如图,在棱长为的正方体中,分别为棱的中点,若点分别为线段上的动点,则的最小值为 _____.
16.正方体的棱长为,设为中点,为线段上的动点,,过点,,的平面截该正方体所得截面记为以下结论正确的有___________填上所有正确的说法的序号
①不可能是菱形;
②可能是五边形;
③时,的面积为;
④时,将棱截成长度比为的两部分.
四、解答题
17.对于精美的礼物,通常人们会用包装纸把礼物包好,还会用彩带捆扎包装好的礼物,有时还会扎出一个花结.这些包装彩带也不便宜,因此在捆扎时不仅要考虑美观 结实,也要考虑尽量地节省包装彩带.以长方体的礼物为例,较为典型的两种捆扎方式分别为“十字”和“对角”,如下图所示.
“十字”捆扎 “对角”捆扎
假设1:将礼物视作一个长方体,其长为4,宽为2 高为1;假设2:不考虑花结处的彩带,将每一段彩带视为线段,且完全位于礼物的表面上;假设3:“十字”捆扎中,长方体表面上的每一段彩带(上底面和下底面各2段,每个侧面各1段)都与其相交的棱垂直;假设4:“对角”捆扎中,以某种方式展开长方体后,长方体表面上的每一段彩带(上底面和下底面各2段,每个侧面各1段)在其表面展开图上均落在同一条直线上.
(1)求“十字”捆扎中彩带的总长度;
(2)根据假设4绘制示意图,求“对角”捆扎中彩带的总长度,并比较两种捆扎方式,给出用彩带捆扎礼物的建议.
18.已知正方体的棱长为2,P是该正方体棱上一点. 若满足的点P的个数,求的表达式.
参考答案:
1.C
【分析】根据正方体的截面分析得到答案.
【详解】用一个平面截正方体,截面图形可能是三角形,四边形,五边形,六边形.
对于A:截面图形如果是三角形,只能是锐角三角形,不可能是直角三角形和钝角三角形.
如图所示的截面三角形.
设,所以,,.
所以由余弦定理得:所以为锐角.
同理可求:为锐角,为锐角.
所以为锐角三角形.故A错误;
对于B:截面图形如果是四边形,可能是正方形,可能是矩形,可能是菱形,可能是一般梯形,也可能是等腰梯形,不可能是直角梯形.
故B错误;
对于C:如图示的截面图为五边形,并且有两个角相等.
故C正确;
对于D:因为正方体有六个面,所以一个平面截正方体,边数最多为6.所以D错误.
故选:C
2.C
【分析】延长,分别交与的延长线于,可得截面过、、,再根据直线与面面相交的性质,分别确定截面与各棱的交点位置,进而确定截面的形状即可.
【详解】因为,故为的中点.又为正方体,故可延长,分别交与的延长线于,设直线分别交于,易得过点、、的面即平面.
因为为中点,且,故,,,所以,故,即.又,故.又为的中点,同理可得,故,所以,,故在线段内.
连接交于,综上可知点、、截正方体的截面为五边形.
故选:C
3.C
【分析】利用正方体的对称性,根据粒子碰撞次数可分别讨论在轴方向上的运动距离,进而判断各情况粒子在容器内的飞行距离,即可得结果.
【详解】因为不能与棱相碰,所以粒子在x,y,z每个方向上的运动路程都不会为0,否则就会在面上运动,必然与棱相碰. 其次,只看x方向上运动(y , z方向同理,因为正方形有对称性),
如果碰撞0次,那么就是运动了1,如果碰撞1次,就是运动了2,以此类推,在x方向上碰撞了n次最后出射的时候在该方向的运动距离就是(n+1),相当于多运动了n. 题目中经过3次碰撞,可以先从碰撞0次入手,3个方向上的位移就是1,1,1(不能与棱相碰),现在碰撞3次,也就是在某个方向上要加距离,每次碰撞则加1:(1)在同一个方向碰撞3次,即距离分别是4,1,1(1,4,1或者1,1,4),结果是. (2)在一个方向碰撞2次,另外一个方向碰撞一次,即3,2,1(2,3,1或1,2,3),结果是根号. (3)在三个方向各碰撞1次,即距离分别是2,2,2,结果是.
综上,粒子飞行距离有三种结果. 这三种情况都可以举出实际例子∶4,1,1,可以看做从A入射,C处射出;3,2,1可以看做从A入射,D处射出;2,2,2可以看做从A入射,B处射出.
故选:C
4.C
【分析】分析可知点、运动的路线呈现周期性变化,且以段为一个周期,确定动点运动完段后、动点运动完段后,这两个动点的位置,即可求得动点、的距离.
【详解】点运动的路线为,
点运动的路线为,
由上可知,点、运动的路线呈现周期性变化,且以段为一个周期,
因为,,
所以,动点运动完段后与点重合,动点运动完段与点重合,
此时,动点、的距离是.
故选:C.
5.D
【分析】利用空间几何体的特征,将沿折起到的位置.使得平面与平面共面,然后两点之间线段最短,再利用余弦定理即可得到答案.
【详解】将沿折起到的位置.使得平面与平面共面,当为线段与的交点时,最小,即最小,则有,
又,所以易得与均为等腰直角三角形,
,
利用余弦定理可知最小值为.
故选:D.
6.A
【分析】作点关于平面的对称点,将点与同侧点距离之和问题转化为相对点距离问题即可.
【详解】如图作点关于的对称点,
,则的最小值为,根据题中数据可知
故选:A
7.A
【分析】可通过确定截面的不同位置去剖开正方体,想象相对应的截面形状,即可确定答案.
【详解】对于A,由于截面中间是矩形,如果可能的话,一定是用和正方体底面平行的截面去剖开
正方体并且是从挖去四棱锥的那部分剖开,但此时剖面中间应该是一个正方形,
因此A图形不可能是截面;
对于B,当从正方体底面的一组相对棱的中点处剖开时,截面正好通过四棱锥顶点,
如图:
此时截面形状如B图形,故B可能是该几何体的截面;
对于C,当截面不经过底面一组相对棱的中点处,并和另一组棱平行去剖开正方体时,
如图中截面PDGH位置:
截面就会如C图形,故C可能是该几何体的截面;
对于D,如图示,按图中截面 的位置去剖开正方体,截面就会如D图形,
故D可能是该几何体的截面;
故答案为:A
8.D
【分析】由题意作出满足条件的图形,由线面位置关系找出截面即可求解
【详解】(1)当即与重合时,过点,,的截面为正方形,不合题设
(2)当,即为中点时,,,则,
所以过点,,的截面为梯形,不合题设
(3)当即与重合时,取中点,中点,连接,,,
因为,所以四边形为平行四边形,所以
因为,所以四边形为平行四边形,所以
所以
所以过点,,的截面为平行四边形,不合题设
(4)当时,过作交线段于,过作交线段于,连接
因为,所以四边形为平行四边形,所以
又,所以
所以过点,,的截面为梯形,不合题设
(5)当时,取中点,在线段上截取,连接,,过作交线段的延长线于点,交线段于点,连接交于点,连接
因为,所以四边形为平行四边形,所以
又,所以
所以过点,,的截面为五边形,符合题设
此时,,
所以的取值范围为
故选:D
9.BC
【分析】根据正方体的截面特点,对四个选项一一判断.
【详解】对于A:截面图形如果是三角形,只能是锐角三角形,不可能是直角三角形和钝角三角形.
如图所示的截面三角形.
设,所以,,.
所以由余弦定理得:所以为锐角.
同理可求:为锐角,为锐角.
所以为锐角三角形.故A不选.
对于B:截面图形如果是四边形,可能是正方形,可能是矩形,可能是菱形,可能是一般梯形,也可能是等腰梯形,不可能是直角梯形.
B选
对于C:当截面为五边形时,不可能出现正五边形.
C选.
对于D:如果截面经过各个棱的中点,得到的是正六边形,如果与各个棱相交,但不全经过各个棱的中点,得到的是边长不全相等的六边形,故D不选.
故选:BC.
10.ABC
【分析】对于A,当点Q与点重合时判断截面形状,对于B,当点Q与点D重合时判断截面形状,对于C,当点Q不与点D,重合时,延长交延长线于,连接交于,连接,可得截面为梯形,当为的中点时进行判断,对于D,由选项ABC判断.
【详解】对于A,当点Q与点重合时,截面图形为等边三角形,所以A正确;
对于B,当点Q与点D重合时,截面图形为矩形,所以B正确;
对于C,当点Q不与点D,重合时,如图,延长交延长线于,连接交于,连接,因为平面∥平面,平面平面,平面 ,所以∥,所以过A,Q,三点的截面为梯形,当为的中点时,可得,所以,所以为的中点,所以,所以此时梯形为等腰梯形,所以C正确,
对于D,由选项ABC,可知截面图形不可能为五边形,
故选:ABC
11.ABC
【分析】从点沿长方体表面到达有三种展开方式,以、、为轴展开,分别求可得答案.
【详解】则从点沿长方体表面到达有三种展开方式,
若以为轴展开,则,
若以为轴展开,则,
若以为轴展开,则.
故选:ABC.
12.ACD
【分析】由公理作出平面与正方体的截面,利用平行线截线段成比例可得点是线段靠近点的三等分点,由对称性知点是线段靠近点的三等分点,
点是线段靠近点的三等分点;再利用等体积法可知,得到平面将正方体分成两部分的体积比为,即可得解.
【详解】解:如图,取的中点,延长,并交于点,连接并延长,设,,
连接并延长交于点,连接,,则四边形就是平面与正方体的截面,
是平面的中心,是中点,,则,
可得点是线段靠近点的三等分点,由对称性知点是线段靠近点的三等分点,
点是线段靠近点的三等分点,故A正确,B错误,C正确;
作出线段的另一个三等分点,作出线段靠近的三等分点,连接,,,,
可知.
,
从而平面将正方体分成两部分的体积比为,
故D正确.
故选:ACD.
13.
【分析】曲面最值问题一般都化曲为平,变成两点间线段最短.
【详解】
如图将正三棱柱侧面展开2次,可知曲面上的最小值即为对角线=
故答案为:
14.21
【分析】作出空间直角坐标系,得出三个坐标轴坐标的变化规律,得出光束的路径,进而求出光反射的次数.
【详解】解:由题意,
在的长方体中,
入射光线与该孔所对应的三条棱的夹角均彼此相同
∴沿对角线入射,
∴各坐标变化规律如下:
建立空间直角坐标系如下图所示:
假设光线从点射入,则光线路径如下:
根据光线路径可知,共经过了21次反射.
∴该束光线经过了21次反射.
故答案为:21.
15.
【分析】由可确定为中点时,最小,取,通过三角形全等可将问题转化为最小值的求解问题,根据三点共线时线段和最小可求得结果.
【详解】
,当为中点时,取得最小值;
在上取一点,使得,
,,,
;
则当三点共线时,最小,即最小,
此时且,的最小值为.
故答案为:.
16.②③④
【分析】对四个说法逐一分析,画出截面,结合线线平行、点共面等知识确定正确答案.
【详解】①当时,与重合,取的中点,连接,
根据正方体的性质可知,且,
所以截面为菱形,
故①错误;
对于②④,当时,
延长,交的延长线于,连接并延长,交于,
设,连接,
由于,结合正方体的性质可知,
结合共面可知为截面,
如图所示,
点是的中点,可得,,
与的交点满足,此时是五边形,且将棱截成长度比为的两部分.
故②④正确;
对于③,当时,根据正方体的性质可知,且,
如图所示,为等腰梯形,
可得,,等腰梯形得高为,
则的面积为.
故③正确.
故答案为:②③④
17.(1)
(2),在实际生活中包装彩带时应选择“对角”捆扎的方式,更节省包装彩带
【分析】(1)直接利用题意即可求出采用“十字”捆扎中彩带的总长度;(2)求出“对角”捆扎中彩带的总长度,比较大小,即可得到答案.
【详解】(1)采用“十字”捆扎中彩带的总长度为;
(2)
由于,因此在实际生活中包装彩带时应选择“对角”捆扎的方式,更节省包装彩带.
18.
【分析】由几何直观,点P所在的位置与的值一一对应,根据正方体的对称性,分别讨论点P在:(1)棱、、、;(2)棱、;(3) 棱、;(4)棱、、、时的可能取值,即可汇总得P的个数及对应m的范围.
【详解】由题,由几何直观可知,点P在正方体的每一条棱上运动时,它所在的位置与的值是一一对应的,先讨论的可能取值:
(1)当点P分别在棱、、、上运动时,如在棱,可得
,其它同理,故此时m的取值范围是;
(2)当点P分别棱、上运动时,如在棱,可得
,其它同理,故此时m的取值范围是;
(3)当点P分别在棱、上运动时,如在棱,可得
,其它同理,故此时m的取值范围是;
(4)当点P分别在棱、、、上运动时,如在棱,可得
,其它同理,故此时m的取值范围是.
综上,点P的个数为可归结为:
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
