8.3 列联表与独立性检验 同步练习-2022-2023学年高二下学期数学人教A版(2019)选择性必修第三册(含解析)
文档属性
| 名称 | 8.3 列联表与独立性检验 同步练习-2022-2023学年高二下学期数学人教A版(2019)选择性必修第三册(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 138.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-07 08:50:14 | ||
图片预览



文档简介
《第三节 列联表与独立性检验》同步练习
附:χ2=,其中n=a+b+c+d.
α 0.1 0.05 0.025 0.01 0.005 0.001
xα 2.706 3.841 5.024 6.635 7.879 10.828
一、基础巩固
知识点1 分类变量与列联表
1.为了解某大学的学生是否爱好体育锻炼,用简单随机抽样的方法在校园内调查了120位学生,得到如下2×2列联表:
单位:人
锻炼 性别 合计
男 女
爱好 a b 73
不爱好 c 25
合计 74
则a-b-c等于( )
A.7 B.8 C.9 D.10
2.(多选)为调查A,B两种药物预防某种疾病的效果,某研究所进行了动物试验.已知参与两种药物试验的动物的品种、状态、数量均相同,图1和图2分别是A,B药物试验结果对应的等高堆积条形图,则( )
A.服用A药物的动物的患病比例低于未服用A药物的动物的患病比例
B.服用A药物对预防该疾病没有效果
C.在对B药物的试验中,患病动物的数量约占参与B药物试验动物总数量的60%
D.B药物比A药物预防该种疾病的效果好
知识点2 独立性检验
3.[2022山东烟台高二下期中]下列关于独立性检验的说法正确的是( )
A.独立性检验是对两个变量是否具有线性相关关系的一种检验
B.独立性检验可以100%确定两个变量之间是否有关系
C.利用独立性检验推断吸烟与患肺病是否有关时,若根据小概率值α=0.01的独立性检验认为吸烟与患肺病有关,则可以说在100个吸烟的人中,有99人患肺病
D.对于独立性检验,统计量χ2的观测值越小,判定“两变量有关系”的可信程度越小
4.[2023安徽芜湖高三上教育教学质检]为了检验某种血清预防感冒的作用,把500名使用血清的人与另外500名未使用血清的人一年中的感冒记录作比较,提出零假设H0:这种血清不能起到预防感冒的作用.若利用2×2列联表计算出χ2,根据小概率值α=0.01的独立性检验,推断H0不成立,则χ2的一个可能取值为( )
A.7.879 B.5.024 C.3.841 D.2.706
5.(多选)[2022陕西西安中学高二下期中]千百年来,我国劳动人民在生产实践中根据云的形状、走向、速度、厚度、颜色等的变化,总结了丰富的“看云识天气”的经验,并将这些经验编成谚语,如“天上钩钩云,地上雨淋淋”“日落云里走,雨在半夜后”……小波同学为了验证“日落云里走,雨在半夜后”,随机观察了他所在地区的100天日落情况和后半夜天气,得到2×2列联表:
单位:天
日落云里走 后半夜天气 合计
下雨 未下雨
出现 25 5 30
未出现 25 45 70
合计 50 50 100
并计算得到χ2≈19.05,下列小波对该地区天气的判断正确的是( )
A.后半夜下雨的概率约为
B.未出现“日落云里走”时,后半夜下雨的概率约为
C.根据小概率值α=0.001的独立性检验,可以推断“‘日落云里走’是否出现”与“后半夜是否下雨”有关
D.根据小概率值α=0.001的独立性检验,若出现“日落云里走”,则后半夜有99.9%的可能会下雨
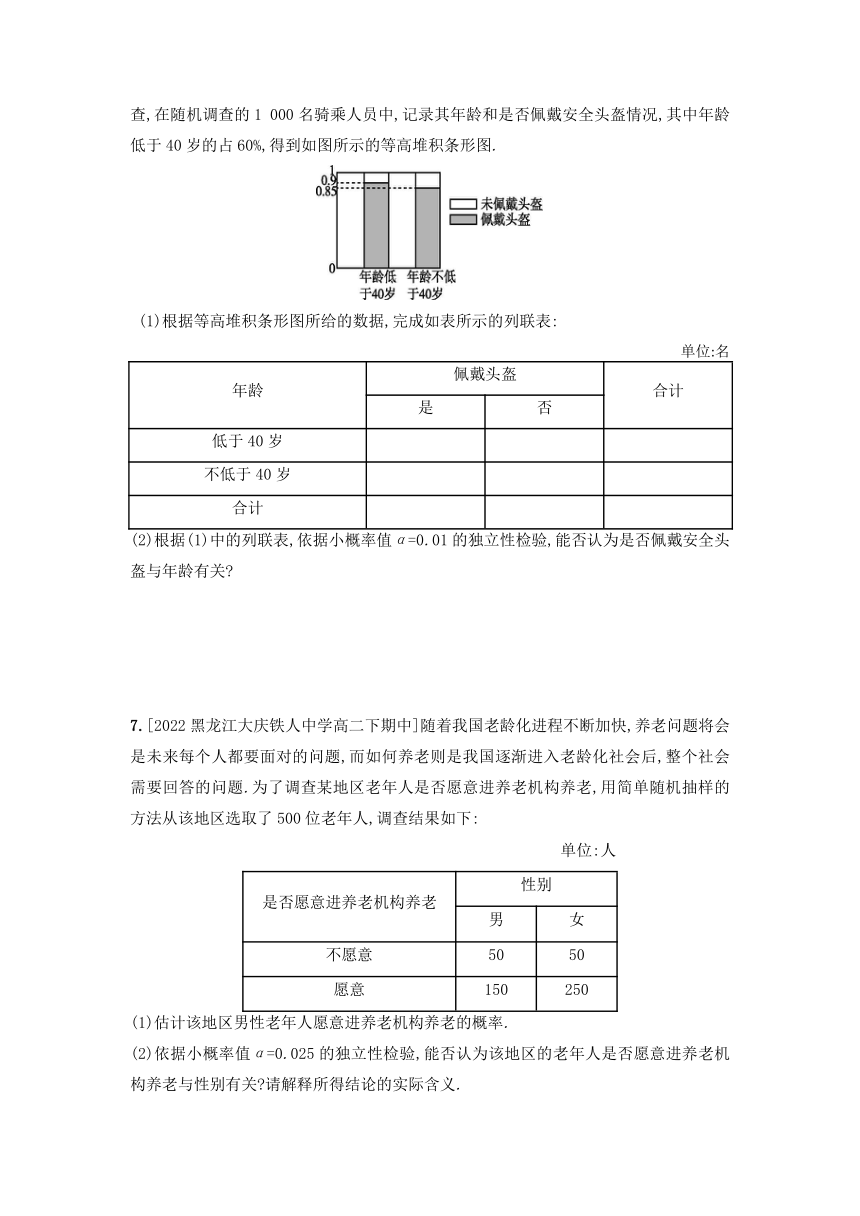
6.[2022山东泰安高二下期末]为持续深化“一盔一带”安全守护行动,有效遏制和减少因电动车闯红灯、逆行、不佩戴安全头盔等行为带来的交通安全隐患,2022年5月以来,泰安根据辖区实际稳步推进“一盔一带”安全守护行动,确保辖区道路交通环境畅通、有序.该行动开展一段时间后,针对电动自行车骑乘人员是否佩戴安全头盔问题进行调查,在随机调查的1 000名骑乘人员中,记录其年龄和是否佩戴安全头盔情况,其中年龄低于40岁的占60%,得到如图所示的等高堆积条形图.
(1)根据等高堆积条形图所给的数据,完成如表所示的列联表:
单位:名
年龄 佩戴头盔 合计
是 否
低于40岁
不低于40岁
合计
(2)根据(1)中的列联表,依据小概率值α=0.01的独立性检验,能否认为是否佩戴安全头盔与年龄有关
7.[2022黑龙江大庆铁人中学高二下期中]随着我国老龄化进程不断加快,养老问题将会是未来每个人都要面对的问题,而如何养老则是我国逐渐进入老龄化社会后,整个社会需要回答的问题.为了调查某地区老年人是否愿意进养老机构养老,用简单随机抽样的方法从该地区选取了500位老年人,调查结果如下:
单位:人
是否愿意进养老机构养老 性别
男 女
不愿意 50 50
愿意 150 250
(1)估计该地区男性老年人愿意进养老机构养老的概率.
(2)依据小概率值α=0.025的独立性检验,能否认为该地区的老年人是否愿意进养老机构养老与性别有关 请解释所得结论的实际含义.
二、能力提升
1.(多选)[2022福建厦门外国语学校高二下期末]某市为了研究该市空气中的PM2.5浓度和SO2浓度之间的关系,环境监测部门对该市空气质量进行调研,随机抽查了100天空气中的PM2.5浓度和SO2浓度(单位:μg/m3),得到如下所示的列联表:
PM2.5浓度 SO2浓度 合计
[0,150] (150,475]
[0,75] 64 16 80
(75,115] 10 10 20
合计 74 26 100
经计算χ2≈7.484 4,则可以推断出( )
A.该市一天空气中PM2.5浓度不超过75 μg/m3,且SO2浓度不超过150 μg/m3的概率估计值是0.64
B.若2×2列联表中的天数都扩大到原来的10倍, χ2的观测值不会发生变化
C.根据α=0.01的独立性检验,可以认为该市一天空气中PM2.5浓度与SO2浓度有关
D.根据α=0.01的独立性检验,可以认为该市一天空气中PM2.5浓度与SO2浓度无关
2.[2023重庆十八中高三上期中]2022全国两会期间,某一电视台对年龄高于30岁和不高于30岁的人是否关注两会进行调查,对高于30岁的调查了45人,不高于30岁的调查了55人,所得数据绘制成如下列联表:
单位:人
年龄 是否关注两会 合计
不关注 关注
高于30岁 p q 45
不高于30岁 15 40 55
合计 p+15 q+40 100
若工作人员从调查的所有人中任取一人,取到关注两会的人的概率为,依据小概率值α=0.005的独立性检验,推断是否关注两会与年龄 (填“有”或“无”)关.
3.[2023四川南充高坪中学高三零诊]2022年6月17日,我国第三艘航空母舰“中国人民解放军海军福建舰”下水试航,这是我国完全自主设计建造的首艘弹射型航空母舰,采用平直通长飞行甲板,配置电磁弹射和阻拦装置,满载排水量8万余吨.“福建舰”的建成、下水及试航,是新时代中国强军建设的重要成果.某校为纪念“福建舰”下水试航,增强学生的国防意识,组织了一次国防知识竞赛,共有100名学生参赛,成绩均在区间[50,100]内,现将成绩制成如图所示的频率分布直方图(每组均包括左端点,最后一组包括右端点).
(1)学校计划对成绩不低于平均分的参赛学生进行奖励,若同一组中的数据用该组区间的中点值为代表,试求受奖励的分数线的估计值.
(2)对这100名参赛学生的成绩按参赛者的性别统计,成绩不低于80分的为“良好”,低于80分的为“不良好”,得到如下未填写完整的列联表.
单位:名
性别 成绩 合计
良好 不良好
男 48
女 16
合计
(i)将列联表填写完整;
(ii)根据小概率值α=0.05的独立性检验,能否认为参赛学生的成绩是否良好与性别有关
4.某中学高三年级组为了解学生主动预习与学习兴趣是否有关,随机抽取一个容量为n的样本进行调查.调查结果表明:主动预习的学生占样本容量的,学习兴趣高的学生占样本容量的,主动预习且学习兴趣高的学生占样本容量的.
(1)完成下面2×2列联表.若依据小概率值α=0.05的χ2独立性检验,认为主动预习与学习兴趣有关,求样本容量n的最小值.
单位:人
预习 学习兴趣 合计
高 一般
主动 n n
不太主动
合计 n n
(2)该校为了提高学生的数学学习兴趣,用分层随机抽样的方法从学习兴趣一般的学生中抽取15人,组成数学学习小组.现从该小组中随机抽取3人进行摸底测试,记3人中不太主动预习的人数为X,求X的分布列和数学期望E(X).
5.某市自启动对“车不让人行为”处罚以来,斑马线前机动车抢行不文明行为得以根本改变,但作为交通重要参与者的行人,闯红灯通行却频有发生,带来了较大的交通安全隐患,同时也使机动车的通畅率降低.该市交管部门在某十字路口根据以往的检测数据,得到行人闯红灯的概率约为0.4,并从穿越该路口的行人中随机抽取了200人进行调查,对是否存在闯红灯情况得到如下2×2列联表
单位:人
闯红灯情况 年龄 合计
30岁及以下 30岁以上
闯红灯 60
未闯红灯 80
合计 200
近期,为了整顿“行人闯红灯”这一项不文明及违法行为,交管部门在该十字路口对闯红灯行人试行经济处罚,并在试行经济处罚后从穿越该路口的行人中随机抽取了200人进行调查,得到下表:
处罚金额/元 5 10 15 20
闯红灯的人数 50 40 20 0
将统计数据所得频率作为概率,完成下列问题.
(1)将2×2列联表填写完整(不需写出填写过程),并根据表中数据分析,在未对闯红灯行人试行经济处罚前,根据小概率值α=0.001的独立性检验,是否可以推断闯红灯与年龄有关
(2)当处罚金额为10元时,行人闯红灯的概率比不进行处罚降低多少.
(3)结合调查结果,谈谈如何治理行人闯红灯现象.
参考答案
一、基础巩固
1.C 根据题意,可得c=120-73-25=22,a=74-22=52,b=73-52=21,所以a-b-c=52-21-22=9.故选C.
2.AD 根据题图,可知服用A药物的动物的患病比例低于未服用A药物的动物的患病比例,所以A正确;服用A药物未患病的动物的频率明显大于未服用A药物的,所以可以认为服用A药物对预防该疾病有一定效果,所以B不正确;在对B药物的试验中,患病动物的数量占参与B药物试验动物总数量的比例为×100%=30%<60%,所以C不正确;B药物试验结果对应的等高堆积条形图显示未服用药与服用药动物的患病数量的差异较A药物试验的大,所以B药物比A药物预防该种疾病的效果好,所以D正确.
3.D
4.A 由题意知χ2≥6.635,结合选项知,A选项符合题意.
5.AC
6.(1)根据等高堆积条形图所给的数据,得列联表如下:
年龄 佩戴头盔 合计
是 否
低于40岁 540 60 600
不低于40岁 340 60 400
合计 880 120 1 000
(2)零假设为H0:佩戴安全头盔与年龄无关.
根据列联表中的数据,计算得χ2=≈5.682<6.635=x0.01,
根据小概率值α=0.01的独立性检验,没有充分证据推断H0不成立,因此可以认为H0成立,即认为是否佩戴安全头盔与年龄无关.
7.(1)由统计数据可知,愿意进养老机构养老的男性老年人为150人,调查的男性老年人的总人数为200,故男性老年人中愿意进养老机构养老的频率为.
根据频率稳定于概率的原理,估计该地区男性老年人愿意进养老机构养老的概率为.
(2)零假设为H0:该地区的老年人是否愿意进养老机构养老与性别无关.
经计算可得χ2=≈5.208>5.024=x0.025,根据小概率值α=0.025的独立性检验,推断H0不成立,即认为该地区的老年人是否愿意进养老机构养老与性别有关,此推断犯错误的概率不大于0.025.
男性老年人愿意进养老机构养老和不愿意进养老机构养老的频率分别为和;女性老年人愿意进养老机构养老和不愿意进养老机构养老的频率分别为和.
由此可见,女性老年人愿意进养老机构养老的频率明显高于男性老年人愿意进养老机构养老的频率.
根据频率稳定于概率的原理,可以推断该地区女性老年人愿意进养老机构养老的概率明显高于男性老年人愿意进养老机构养老的概率.
二、能力提升
1.AC
2.有 解析由题知解得q=20,p=25,所以χ2=≈8.249>7.879=x0.005,所以依据小概率值α=0.005的独立性检验,推断是否关注两会与年龄有关.
3.(1)由频率分布直方图可知10(0.006+0.008+a+0.026+0.042)=1,解得a=0.018,
所以平均分的估计值为0.08×55+0.26×65+0.42×75+0.18×85+0.06×95=73.8,
故受奖励的分数线的估计值为73.8.
(2)(i)填写列联表如下:
性别 成绩 合计
良好 不良好
男 8 40 48
女 16 36 52
合计 24 76 100
(ii)零假设为H0:成绩与性别独立,即参赛学生的成绩是否良好与性别无关.
由列联表得χ2=≈2.72<3.841=x0.05,所以根据小概率值α=0.05的独立性检验,没有充分证据推断H0不成立,因此可以认为H0成立,即认为参赛学生的成绩是否良好与性别无关.
4.(1)2×2列联表如下:
预习 学习兴趣 合计
高 一般
主动 n n n
不太主动 n n n
合计 n n n
χ2=,
因为依据小概率值α=0.05的χ2独立性检验,认为主动预习与学习兴趣有关,所以≥3.841,解得n≥199.732,
由题设知,正整数n是15的倍数,即nmin=210,
所以样本容量n的最小值为210.
(2)由(1)知,学习兴趣一般的学生中,主动预习与不太主动预习的学生人数之比为4∶1,
因此,用分层随机抽样,从学习兴趣一般的学生中抽取15人,其中不太主动预习的人数为3.
则X的可能取值为0,1,2,3,且
P(X=0)=,P(X=1)=,
P(X=2)=,P(X=3)=,
所以X的分布列为
X 0 1 2 3
P
所以E(X)=0×+1×+2×+3×.
5.(1)
闯红灯情况 年龄 合计
30岁及以下 30岁以上
闯红灯 20 60 80
未闯红灯 80 40 120
合计 100 100 200
零假设为H0:闯红灯与年龄无关.
由表中数据,得χ2=≈33.333>10.828=x0.001,
根据小概率值α=0.001的独立性检验,推断H0不成立,即认为闯红灯与年龄有关.
(2)未进行处罚前,行人闯红灯的概率约为0.4,当处罚金额为10元时,行人闯红灯的概率约为=0.2,
故当处罚金额为10元时,行人闯红灯的概率比不进行处罚降低0.2.
(3)①根据调查数据显示,行人闯红灯与年龄有明显关系,可以针对30岁以上人群开展“道路安全”宣传教育;②由于试行经济处罚可以明显降低行人闯红灯的概率,则可以进行适当经济处罚来降低行人闯红灯的概率.
附:χ2=,其中n=a+b+c+d.
α 0.1 0.05 0.025 0.01 0.005 0.001
xα 2.706 3.841 5.024 6.635 7.879 10.828
一、基础巩固
知识点1 分类变量与列联表
1.为了解某大学的学生是否爱好体育锻炼,用简单随机抽样的方法在校园内调查了120位学生,得到如下2×2列联表:
单位:人
锻炼 性别 合计
男 女
爱好 a b 73
不爱好 c 25
合计 74
则a-b-c等于( )
A.7 B.8 C.9 D.10
2.(多选)为调查A,B两种药物预防某种疾病的效果,某研究所进行了动物试验.已知参与两种药物试验的动物的品种、状态、数量均相同,图1和图2分别是A,B药物试验结果对应的等高堆积条形图,则( )
A.服用A药物的动物的患病比例低于未服用A药物的动物的患病比例
B.服用A药物对预防该疾病没有效果
C.在对B药物的试验中,患病动物的数量约占参与B药物试验动物总数量的60%
D.B药物比A药物预防该种疾病的效果好
知识点2 独立性检验
3.[2022山东烟台高二下期中]下列关于独立性检验的说法正确的是( )
A.独立性检验是对两个变量是否具有线性相关关系的一种检验
B.独立性检验可以100%确定两个变量之间是否有关系
C.利用独立性检验推断吸烟与患肺病是否有关时,若根据小概率值α=0.01的独立性检验认为吸烟与患肺病有关,则可以说在100个吸烟的人中,有99人患肺病
D.对于独立性检验,统计量χ2的观测值越小,判定“两变量有关系”的可信程度越小
4.[2023安徽芜湖高三上教育教学质检]为了检验某种血清预防感冒的作用,把500名使用血清的人与另外500名未使用血清的人一年中的感冒记录作比较,提出零假设H0:这种血清不能起到预防感冒的作用.若利用2×2列联表计算出χ2,根据小概率值α=0.01的独立性检验,推断H0不成立,则χ2的一个可能取值为( )
A.7.879 B.5.024 C.3.841 D.2.706
5.(多选)[2022陕西西安中学高二下期中]千百年来,我国劳动人民在生产实践中根据云的形状、走向、速度、厚度、颜色等的变化,总结了丰富的“看云识天气”的经验,并将这些经验编成谚语,如“天上钩钩云,地上雨淋淋”“日落云里走,雨在半夜后”……小波同学为了验证“日落云里走,雨在半夜后”,随机观察了他所在地区的100天日落情况和后半夜天气,得到2×2列联表:
单位:天
日落云里走 后半夜天气 合计
下雨 未下雨
出现 25 5 30
未出现 25 45 70
合计 50 50 100
并计算得到χ2≈19.05,下列小波对该地区天气的判断正确的是( )
A.后半夜下雨的概率约为
B.未出现“日落云里走”时,后半夜下雨的概率约为
C.根据小概率值α=0.001的独立性检验,可以推断“‘日落云里走’是否出现”与“后半夜是否下雨”有关
D.根据小概率值α=0.001的独立性检验,若出现“日落云里走”,则后半夜有99.9%的可能会下雨
6.[2022山东泰安高二下期末]为持续深化“一盔一带”安全守护行动,有效遏制和减少因电动车闯红灯、逆行、不佩戴安全头盔等行为带来的交通安全隐患,2022年5月以来,泰安根据辖区实际稳步推进“一盔一带”安全守护行动,确保辖区道路交通环境畅通、有序.该行动开展一段时间后,针对电动自行车骑乘人员是否佩戴安全头盔问题进行调查,在随机调查的1 000名骑乘人员中,记录其年龄和是否佩戴安全头盔情况,其中年龄低于40岁的占60%,得到如图所示的等高堆积条形图.
(1)根据等高堆积条形图所给的数据,完成如表所示的列联表:
单位:名
年龄 佩戴头盔 合计
是 否
低于40岁
不低于40岁
合计
(2)根据(1)中的列联表,依据小概率值α=0.01的独立性检验,能否认为是否佩戴安全头盔与年龄有关
7.[2022黑龙江大庆铁人中学高二下期中]随着我国老龄化进程不断加快,养老问题将会是未来每个人都要面对的问题,而如何养老则是我国逐渐进入老龄化社会后,整个社会需要回答的问题.为了调查某地区老年人是否愿意进养老机构养老,用简单随机抽样的方法从该地区选取了500位老年人,调查结果如下:
单位:人
是否愿意进养老机构养老 性别
男 女
不愿意 50 50
愿意 150 250
(1)估计该地区男性老年人愿意进养老机构养老的概率.
(2)依据小概率值α=0.025的独立性检验,能否认为该地区的老年人是否愿意进养老机构养老与性别有关 请解释所得结论的实际含义.
二、能力提升
1.(多选)[2022福建厦门外国语学校高二下期末]某市为了研究该市空气中的PM2.5浓度和SO2浓度之间的关系,环境监测部门对该市空气质量进行调研,随机抽查了100天空气中的PM2.5浓度和SO2浓度(单位:μg/m3),得到如下所示的列联表:
PM2.5浓度 SO2浓度 合计
[0,150] (150,475]
[0,75] 64 16 80
(75,115] 10 10 20
合计 74 26 100
经计算χ2≈7.484 4,则可以推断出( )
A.该市一天空气中PM2.5浓度不超过75 μg/m3,且SO2浓度不超过150 μg/m3的概率估计值是0.64
B.若2×2列联表中的天数都扩大到原来的10倍, χ2的观测值不会发生变化
C.根据α=0.01的独立性检验,可以认为该市一天空气中PM2.5浓度与SO2浓度有关
D.根据α=0.01的独立性检验,可以认为该市一天空气中PM2.5浓度与SO2浓度无关
2.[2023重庆十八中高三上期中]2022全国两会期间,某一电视台对年龄高于30岁和不高于30岁的人是否关注两会进行调查,对高于30岁的调查了45人,不高于30岁的调查了55人,所得数据绘制成如下列联表:
单位:人
年龄 是否关注两会 合计
不关注 关注
高于30岁 p q 45
不高于30岁 15 40 55
合计 p+15 q+40 100
若工作人员从调查的所有人中任取一人,取到关注两会的人的概率为,依据小概率值α=0.005的独立性检验,推断是否关注两会与年龄 (填“有”或“无”)关.
3.[2023四川南充高坪中学高三零诊]2022年6月17日,我国第三艘航空母舰“中国人民解放军海军福建舰”下水试航,这是我国完全自主设计建造的首艘弹射型航空母舰,采用平直通长飞行甲板,配置电磁弹射和阻拦装置,满载排水量8万余吨.“福建舰”的建成、下水及试航,是新时代中国强军建设的重要成果.某校为纪念“福建舰”下水试航,增强学生的国防意识,组织了一次国防知识竞赛,共有100名学生参赛,成绩均在区间[50,100]内,现将成绩制成如图所示的频率分布直方图(每组均包括左端点,最后一组包括右端点).
(1)学校计划对成绩不低于平均分的参赛学生进行奖励,若同一组中的数据用该组区间的中点值为代表,试求受奖励的分数线的估计值.
(2)对这100名参赛学生的成绩按参赛者的性别统计,成绩不低于80分的为“良好”,低于80分的为“不良好”,得到如下未填写完整的列联表.
单位:名
性别 成绩 合计
良好 不良好
男 48
女 16
合计
(i)将列联表填写完整;
(ii)根据小概率值α=0.05的独立性检验,能否认为参赛学生的成绩是否良好与性别有关
4.某中学高三年级组为了解学生主动预习与学习兴趣是否有关,随机抽取一个容量为n的样本进行调查.调查结果表明:主动预习的学生占样本容量的,学习兴趣高的学生占样本容量的,主动预习且学习兴趣高的学生占样本容量的.
(1)完成下面2×2列联表.若依据小概率值α=0.05的χ2独立性检验,认为主动预习与学习兴趣有关,求样本容量n的最小值.
单位:人
预习 学习兴趣 合计
高 一般
主动 n n
不太主动
合计 n n
(2)该校为了提高学生的数学学习兴趣,用分层随机抽样的方法从学习兴趣一般的学生中抽取15人,组成数学学习小组.现从该小组中随机抽取3人进行摸底测试,记3人中不太主动预习的人数为X,求X的分布列和数学期望E(X).
5.某市自启动对“车不让人行为”处罚以来,斑马线前机动车抢行不文明行为得以根本改变,但作为交通重要参与者的行人,闯红灯通行却频有发生,带来了较大的交通安全隐患,同时也使机动车的通畅率降低.该市交管部门在某十字路口根据以往的检测数据,得到行人闯红灯的概率约为0.4,并从穿越该路口的行人中随机抽取了200人进行调查,对是否存在闯红灯情况得到如下2×2列联表
单位:人
闯红灯情况 年龄 合计
30岁及以下 30岁以上
闯红灯 60
未闯红灯 80
合计 200
近期,为了整顿“行人闯红灯”这一项不文明及违法行为,交管部门在该十字路口对闯红灯行人试行经济处罚,并在试行经济处罚后从穿越该路口的行人中随机抽取了200人进行调查,得到下表:
处罚金额/元 5 10 15 20
闯红灯的人数 50 40 20 0
将统计数据所得频率作为概率,完成下列问题.
(1)将2×2列联表填写完整(不需写出填写过程),并根据表中数据分析,在未对闯红灯行人试行经济处罚前,根据小概率值α=0.001的独立性检验,是否可以推断闯红灯与年龄有关
(2)当处罚金额为10元时,行人闯红灯的概率比不进行处罚降低多少.
(3)结合调查结果,谈谈如何治理行人闯红灯现象.
参考答案
一、基础巩固
1.C 根据题意,可得c=120-73-25=22,a=74-22=52,b=73-52=21,所以a-b-c=52-21-22=9.故选C.
2.AD 根据题图,可知服用A药物的动物的患病比例低于未服用A药物的动物的患病比例,所以A正确;服用A药物未患病的动物的频率明显大于未服用A药物的,所以可以认为服用A药物对预防该疾病有一定效果,所以B不正确;在对B药物的试验中,患病动物的数量占参与B药物试验动物总数量的比例为×100%=30%<60%,所以C不正确;B药物试验结果对应的等高堆积条形图显示未服用药与服用药动物的患病数量的差异较A药物试验的大,所以B药物比A药物预防该种疾病的效果好,所以D正确.
3.D
4.A 由题意知χ2≥6.635,结合选项知,A选项符合题意.
5.AC
6.(1)根据等高堆积条形图所给的数据,得列联表如下:
年龄 佩戴头盔 合计
是 否
低于40岁 540 60 600
不低于40岁 340 60 400
合计 880 120 1 000
(2)零假设为H0:佩戴安全头盔与年龄无关.
根据列联表中的数据,计算得χ2=≈5.682<6.635=x0.01,
根据小概率值α=0.01的独立性检验,没有充分证据推断H0不成立,因此可以认为H0成立,即认为是否佩戴安全头盔与年龄无关.
7.(1)由统计数据可知,愿意进养老机构养老的男性老年人为150人,调查的男性老年人的总人数为200,故男性老年人中愿意进养老机构养老的频率为.
根据频率稳定于概率的原理,估计该地区男性老年人愿意进养老机构养老的概率为.
(2)零假设为H0:该地区的老年人是否愿意进养老机构养老与性别无关.
经计算可得χ2=≈5.208>5.024=x0.025,根据小概率值α=0.025的独立性检验,推断H0不成立,即认为该地区的老年人是否愿意进养老机构养老与性别有关,此推断犯错误的概率不大于0.025.
男性老年人愿意进养老机构养老和不愿意进养老机构养老的频率分别为和;女性老年人愿意进养老机构养老和不愿意进养老机构养老的频率分别为和.
由此可见,女性老年人愿意进养老机构养老的频率明显高于男性老年人愿意进养老机构养老的频率.
根据频率稳定于概率的原理,可以推断该地区女性老年人愿意进养老机构养老的概率明显高于男性老年人愿意进养老机构养老的概率.
二、能力提升
1.AC
2.有 解析由题知解得q=20,p=25,所以χ2=≈8.249>7.879=x0.005,所以依据小概率值α=0.005的独立性检验,推断是否关注两会与年龄有关.
3.(1)由频率分布直方图可知10(0.006+0.008+a+0.026+0.042)=1,解得a=0.018,
所以平均分的估计值为0.08×55+0.26×65+0.42×75+0.18×85+0.06×95=73.8,
故受奖励的分数线的估计值为73.8.
(2)(i)填写列联表如下:
性别 成绩 合计
良好 不良好
男 8 40 48
女 16 36 52
合计 24 76 100
(ii)零假设为H0:成绩与性别独立,即参赛学生的成绩是否良好与性别无关.
由列联表得χ2=≈2.72<3.841=x0.05,所以根据小概率值α=0.05的独立性检验,没有充分证据推断H0不成立,因此可以认为H0成立,即认为参赛学生的成绩是否良好与性别无关.
4.(1)2×2列联表如下:
预习 学习兴趣 合计
高 一般
主动 n n n
不太主动 n n n
合计 n n n
χ2=,
因为依据小概率值α=0.05的χ2独立性检验,认为主动预习与学习兴趣有关,所以≥3.841,解得n≥199.732,
由题设知,正整数n是15的倍数,即nmin=210,
所以样本容量n的最小值为210.
(2)由(1)知,学习兴趣一般的学生中,主动预习与不太主动预习的学生人数之比为4∶1,
因此,用分层随机抽样,从学习兴趣一般的学生中抽取15人,其中不太主动预习的人数为3.
则X的可能取值为0,1,2,3,且
P(X=0)=,P(X=1)=,
P(X=2)=,P(X=3)=,
所以X的分布列为
X 0 1 2 3
P
所以E(X)=0×+1×+2×+3×.
5.(1)
闯红灯情况 年龄 合计
30岁及以下 30岁以上
闯红灯 20 60 80
未闯红灯 80 40 120
合计 100 100 200
零假设为H0:闯红灯与年龄无关.
由表中数据,得χ2=≈33.333>10.828=x0.001,
根据小概率值α=0.001的独立性检验,推断H0不成立,即认为闯红灯与年龄有关.
(2)未进行处罚前,行人闯红灯的概率约为0.4,当处罚金额为10元时,行人闯红灯的概率约为=0.2,
故当处罚金额为10元时,行人闯红灯的概率比不进行处罚降低0.2.
(3)①根据调查数据显示,行人闯红灯与年龄有明显关系,可以针对30岁以上人群开展“道路安全”宣传教育;②由于试行经济处罚可以明显降低行人闯红灯的概率,则可以进行适当经济处罚来降低行人闯红灯的概率.
