5.3.1 函数的单调性同步练习(含解析)
文档属性
| 名称 | 5.3.1 函数的单调性同步练习(含解析) | 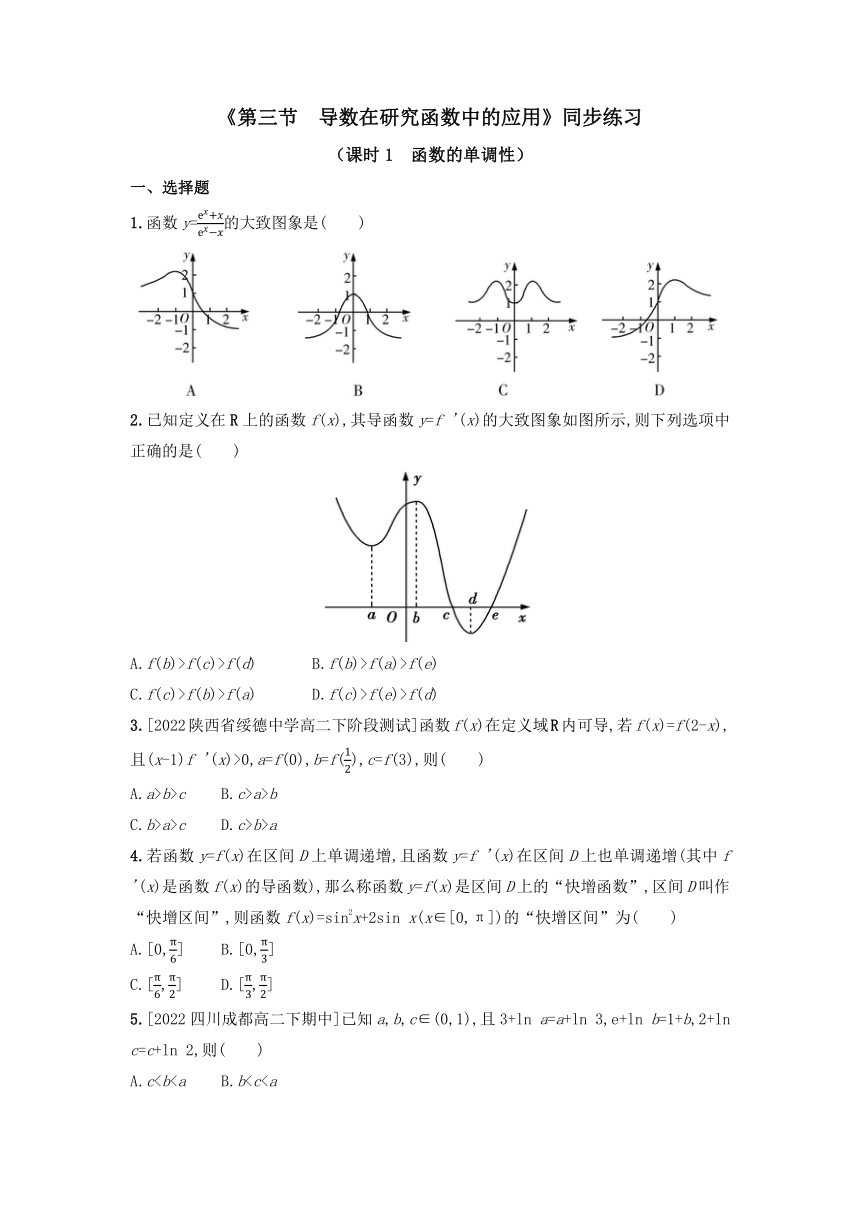 | |
| 格式 | docx | ||
| 文件大小 | 111.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-07 08:55:35 | ||
图片预览



文档简介
《第三节 导数在研究函数中的应用》同步练习
(课时1 函数的单调性)
一、选择题
1.函数y=的大致图象是( )
2.已知定义在R上的函数f(x),其导函数y=f '(x)的大致图象如图所示,则下列选项中正确的是( )
A.f(b)>f(c)>f(d) B.f(b)>f(a)>f(e)
C.f(c)>f(b)>f(a) D.f(c)>f(e)>f(d)
3.[2022陕西省绥德中学高二下阶段测试]函数f(x)在定义域R内可导,若f(x)=f(2-x),且(x-1)f '(x)>0,a=f(0),b=f(),c=f(3),则( )
A.a>b>c B.c>a>b
C.b>a>c D.c>b>a
4.若函数y=f(x)在区间D上单调递增,且函数y=f '(x)在区间D上也单调递增(其中f '(x)是函数f(x)的导函数),那么称函数y=f(x)是区间D上的“快增函数”,区间D叫作“快增区间”,则函数f(x)=sin2x+2sin x(x∈[0,π])的“快增区间”为( )
A.[0,] B.[0,]
C.[,] D.[,]
5.[2022四川成都高二下期中]已知a,b,c∈(0,1),且3+ln a=a+ln 3,e+ln b=1+b,2+ln c=c+ln 2,则( )
A.cC.a6.(多选)[2022河北定州高二下期中]已知定义在[0,)上的函数f(x)的导函数为f '(x),且f(0)=0,f '(x)cos x+f(x)sin x<0,则( )
A.f()C.f()>f() D.f()>f()
7.定义在R上的奇函数f(x)的图象连续,其导函数为f '(x),对任意正实数x恒有xf '(x)>2f(-x).若g(x)=x2f(x),则不等式g(log3(x2-1))+g(-1)<0的解集是( )
A.(0,2) B.(-2,2)
C.(-,2) D.(-2,-1)∪(1,2)
二、非选择题
8.[2022北京和平街一中高二下月考]写出一个同时具有下列性质①②③的函数f(x)= .
①f(x1)f(x2)=f(x1+x2);②f '(x)>0;③f '(x)>f(x).
9.[2022吉林白山抚松一中高二下月考]已知定义在R上的可导函数f(x)的导函数为f '(x),满足f '(x)10.[2022山东菏泽东明一中高二下月考]在①函数f(x)的图象在点(2,f(2))处的切线斜率为2a,②函数f(x)的图象在点(1,f(1))处的切线与直线x+y+1=0垂直,③函数f(x)的图象在点(1,f(1))处的切线与直线4x-y=0平行这三个条件中任选一个,补充在横线上,并解答问题.
已知函数f(x)=x2+2aln x.
(1)若 ,求实数a的值;
(2)若函数g(x)=+f(x)在[1,2]上单调递减,求实数a的取值范围.
11.[2022河北部分名校高二下期中]已知函数f(x)=xex+ax2+2ax,a∈R.
(1)若a=1,求f(x)的图象在x=-1处的切线方程;
(2)讨论f(x)的单调性.
12.已知函数f(x)=1++ln x+.
(1)判断函数f(x)的单调性;
(2)记g(x)=,试证明:当x>1时,f(x)>(e+1)g(x).
13.已知函数f(x)=2acos x-+1,f '(x)是f(x)的导数,且f '()=0.
(1)求a的值,并讨论f(x)在(0,)上的单调性;
(2)讨论函数f(x)在[2kπ+,2kπ+π](k∈N)上的零点个数.
参考答案
一、选择题
1.D y==1+,则y'=,所以当x>1时,y'<0,当x<1时,y'>0,故此函数在(-∞,1)上单调递增,在(1,+∞)上单调递减,所以D正确.
2.C 由题图,可得当x∈(-∞,c)时,f '(x)>0;当x∈(c,e)时,f '(x)<0;当x∈(e,+∞)时,f '(x)>0.因此,函数f(x)在(-∞,c)上单调递增,在(c,e)上单调递减,在(e,+∞)上单调递增.又af(b)>f(a).
3.B 因为f(x)=f(2-x),所以函数f(x)的图象关于直线x=1对称,又(x-1)f '(x)>0,所以当x>1时,f '(x)>0,所以函数f(x)在(1,+∞)上单调递增.又a=f(0)=f(2),b=f()=f(),所以f()a>b.
4.A 由题知f '(x)=2sin xcos x+2cos x=2cos x(sin x+1).因为sin x+1≥0恒成立,当x∈[0,]时,cos x≥0,所以f '(x)≥0,即f(x)单调递增;当x∈(,π)时,cos x<0,所以f '(x)<0,即f(x)单调递减.令g(x)=f '(x)=2sin xcos x+2cos x,x∈[0,],则g'(x)=2cos2x-2sin2x- 2sin x=2-4sin2x-2sin x.令t=sin x, 则t∈[0,1],令h(t)=-4t2-2t+2=-2(2t-1)(t+1)(t∈[0,1]),所以当t∈[0,]时,h(t)≥0,即x∈[0,]时,g'(x)≥0,g(x)单调递增,所以函数f(x)=sin2 x+2sin x(x∈[0,π])的“快增区间”为[0,].故选A.
5.D 3+ln a=a+ln 3 ln a-a=ln 3-3,e+ln b=1+b ln b-b=1-e=ln e-e,2+ln c=c+ln 2 ln c-c=ln 2-2.令f(x)=ln x-x(x>0),则f'(x)=-1,当00,当x>1时,f'(x)<0,所以f(x)在(0,1)上单调递增,在(1,+∞)上单调递减,显然3>e>2>1,所以f(3)6.BCD 设F(x)=,则F'(x)=<0,所以F(x)在[0,)上单调递减.
7.D 因为f(x)是定义在R上的奇函数,所以g(x)为奇函数.因为对于正实数x,有xf '(x)>2f(-x)=-2f(x),即xf '(x)+2f(x)>0,所以当x>0时,g'(x)=2xf(x)+x2f '(x)=x[2f(x)+xf '(x)]>0,所以g(x)=x2f(x)在(0,+∞)上单调递增,易知g(x)的图象在R上连续,又g(x)为奇函数,所以g(x)为R上的增函数.由g(log3(x2-1))+g(-1)<0得g(log3(x2-1))<-g(-1)=g(1),所以log3(x2-1)<1,即0二、非选择题
8.e2x(答案不唯一) 解析由①知函数f(x)可以是指数函数,由②可知函数f(x)单调递增.设f(x)=ax(a>0),由f '(x)=axln a>ax,得a>e.满足题意的函数可以为f(x)=e2x.(注:底数大于e的指数函数均可.)
9.(0,+∞) 解析令g(x)=,因为f '(x)0.
10.(1)方案一 选条件①.
由题意得f '(x)=2x+.
由已知得f '(2)=2a,即=2a,解得a=4.
方案二 选条件②.
由题意得f '(x)=2x+.
因为直线x+y+1=0的斜率为-,所以f '(1)=2,即2+2a=2,解得a=0.
方案三 选条件③.
由题意得f '(x)=2x+.
因为直线4x-y=0的斜率为4,所以f '(1)=4,
即2+2a=4,解得a=1.
(2)由题意得g'(x)=-+2x+.
由函数g(x)在[1,2]上单调递减,可得g'(x)≤0在[1,2]上恒成立,即-+2x+≤0在[1,2]上恒成立,即a≤-x2在[1,2]上恒成立.
令h(x)=-x2,x∈[1,2],则h'(x)=--2x<0,即h(x)在[1,2]上单调递减,所以h(x)min=h(2)=-,
故a≤-,即实数a的取值范围为(-∞,-].
11.(1)因为a=1,所以f(x)=xex+x2+2x,
则f '(x)=ex+xex+2x+2=(x+1)(ex+2),
则f(-1)=-,f '(-1)=0,
故f(x)的图象在x=-1处的切线方程为y=-.
(2)f '(x)=(x+1)ex+2ax+2a=(x+1)(ex+2a).
若a≥0,则ex+2a>0恒成立,
所以当x∈(-∞,-1)时,f '(x)<0,函数f(x)单调递减;
当x∈(-1,+∞)时,f '(x)>0,函数f(x)单调递增.
若a<0,则由ex+2a=0,得x=ln(-2a).
当ln(-2a)<-1,即-若x∈(-∞,ln(-2a)),则f '(x)>0,函数f(x)单调递增;若x∈(ln(-2a),-1),则f '(x)<0,函数f(x)单调递减;若x∈(-1,+∞),则f '(x)>0,函数f(x)单调递增.
当ln(-2a)=-1,即a=-时,f '(x)≥0在R上恒成立,函数f(x)单调递增.
当ln(-2a)>-1,即a<-时,
若x∈(-∞,-1),则f '(x)>0,函数f(x)单调递增;若x∈(-1,ln(-2a)),则f '(x)<0,函数f(x)单调递减;若x∈(ln(-2a),+∞),则f '(x)>0,函数f(x)单调递增.
综上所述,当a≥0时,f(x)的单调递增区间为(-1,+∞),单调递减区间为(-∞,-1);
当-当a=-时,f(x)在R上单调递增;
当a<-时,f(x)的单调递增区间为(-∞,-1)和(ln(-2a),+∞),单调递减区间为(-1,ln(-2a)).
12.(1)由题意,得f(x)的定义域为(0,+∞),f '(x)=.
由y=x,y=ln x的图象(如图所示)可知,在(0,+∞)上x>ln x恒成立,所以f '(x)>0,
所以f(x)在(0,+∞)上单调递增.
(2)由(1)知f(x)在(0,+∞)上单调递增,故当x>1时,f(x)>f(1)=2,故 .
g'(x)=,因为x>1,所以1-ex<0,所以g'(x)<0,即g(x)在(1,+∞)上单调递减,
所以当x>1时,g(x)所以>g(x),即f(x)>(e+1)g(x).
13.(1)由题意得f '(x)=-2asin x+.
因为f '()=0,所以-2a+1=0,解得a=,
所以f '(x)=-sin x+.
令φ(x)=f '(x)=-sin x+,则φ'(x)=-cos x-,
当x∈(0,)时,φ'(x)<0,故f '(x)在(0,)上单调递减,
所以f '(x)>f '()=0,故f(x)在(0,)上单调递增.
(2)由(1)知f(x)=cos x-+1,
令h(x)=f(x)=(1+cos x)-1,
因为≠0,所以f(x)与h(x)有相同的零点个数,
h'(x)=(-sin x+1+cos x)=[1-sin(x-)],
当x∈[2kπ+,2kπ+π](k∈N)时,x-∈[2kπ+,2kπ+](k∈N),所以sin(x-)∈[,1],则sin(x-)∈[1,],故h'(x)≤0,所以h(x)在[2kπ+,2kπ+π](k∈N)上单调递减.
因为k∈N,h(2kπ+)=e2kπ-1≥0,h(2kπ+π)=-1<0,
所以由函数零点存在定理可知,h(x)在[2kπ+,2kπ+π](k∈N)上只有一个零点,
故函数f(x)在[2kπ+,2kπ+π](k∈N)上只有一个零点.
(课时1 函数的单调性)
一、选择题
1.函数y=的大致图象是( )
2.已知定义在R上的函数f(x),其导函数y=f '(x)的大致图象如图所示,则下列选项中正确的是( )
A.f(b)>f(c)>f(d) B.f(b)>f(a)>f(e)
C.f(c)>f(b)>f(a) D.f(c)>f(e)>f(d)
3.[2022陕西省绥德中学高二下阶段测试]函数f(x)在定义域R内可导,若f(x)=f(2-x),且(x-1)f '(x)>0,a=f(0),b=f(),c=f(3),则( )
A.a>b>c B.c>a>b
C.b>a>c D.c>b>a
4.若函数y=f(x)在区间D上单调递增,且函数y=f '(x)在区间D上也单调递增(其中f '(x)是函数f(x)的导函数),那么称函数y=f(x)是区间D上的“快增函数”,区间D叫作“快增区间”,则函数f(x)=sin2x+2sin x(x∈[0,π])的“快增区间”为( )
A.[0,] B.[0,]
C.[,] D.[,]
5.[2022四川成都高二下期中]已知a,b,c∈(0,1),且3+ln a=a+ln 3,e+ln b=1+b,2+ln c=c+ln 2,则( )
A.c
A.f()
7.定义在R上的奇函数f(x)的图象连续,其导函数为f '(x),对任意正实数x恒有xf '(x)>2f(-x).若g(x)=x2f(x),则不等式g(log3(x2-1))+g(-1)<0的解集是( )
A.(0,2) B.(-2,2)
C.(-,2) D.(-2,-1)∪(1,2)
二、非选择题
8.[2022北京和平街一中高二下月考]写出一个同时具有下列性质①②③的函数f(x)= .
①f(x1)f(x2)=f(x1+x2);②f '(x)>0;③f '(x)>f(x).
9.[2022吉林白山抚松一中高二下月考]已知定义在R上的可导函数f(x)的导函数为f '(x),满足f '(x)
已知函数f(x)=x2+2aln x.
(1)若 ,求实数a的值;
(2)若函数g(x)=+f(x)在[1,2]上单调递减,求实数a的取值范围.
11.[2022河北部分名校高二下期中]已知函数f(x)=xex+ax2+2ax,a∈R.
(1)若a=1,求f(x)的图象在x=-1处的切线方程;
(2)讨论f(x)的单调性.
12.已知函数f(x)=1++ln x+.
(1)判断函数f(x)的单调性;
(2)记g(x)=,试证明:当x>1时,f(x)>(e+1)g(x).
13.已知函数f(x)=2acos x-+1,f '(x)是f(x)的导数,且f '()=0.
(1)求a的值,并讨论f(x)在(0,)上的单调性;
(2)讨论函数f(x)在[2kπ+,2kπ+π](k∈N)上的零点个数.
参考答案
一、选择题
1.D y==1+,则y'=,所以当x>1时,y'<0,当x<1时,y'>0,故此函数在(-∞,1)上单调递增,在(1,+∞)上单调递减,所以D正确.
2.C 由题图,可得当x∈(-∞,c)时,f '(x)>0;当x∈(c,e)时,f '(x)<0;当x∈(e,+∞)时,f '(x)>0.因此,函数f(x)在(-∞,c)上单调递增,在(c,e)上单调递减,在(e,+∞)上单调递增.又a
3.B 因为f(x)=f(2-x),所以函数f(x)的图象关于直线x=1对称,又(x-1)f '(x)>0,所以当x>1时,f '(x)>0,所以函数f(x)在(1,+∞)上单调递增.又a=f(0)=f(2),b=f()=f(),所以f()
4.A 由题知f '(x)=2sin xcos x+2cos x=2cos x(sin x+1).因为sin x+1≥0恒成立,当x∈[0,]时,cos x≥0,所以f '(x)≥0,即f(x)单调递增;当x∈(,π)时,cos x<0,所以f '(x)<0,即f(x)单调递减.令g(x)=f '(x)=2sin xcos x+2cos x,x∈[0,],则g'(x)=2cos2x-2sin2x- 2sin x=2-4sin2x-2sin x.令t=sin x, 则t∈[0,1],令h(t)=-4t2-2t+2=-2(2t-1)(t+1)(t∈[0,1]),所以当t∈[0,]时,h(t)≥0,即x∈[0,]时,g'(x)≥0,g(x)单调递增,所以函数f(x)=sin2 x+2sin x(x∈[0,π])的“快增区间”为[0,].故选A.
5.D 3+ln a=a+ln 3 ln a-a=ln 3-3,e+ln b=1+b ln b-b=1-e=ln e-e,2+ln c=c+ln 2 ln c-c=ln 2-2.令f(x)=ln x-x(x>0),则f'(x)=-1,当0
7.D 因为f(x)是定义在R上的奇函数,所以g(x)为奇函数.因为对于正实数x,有xf '(x)>2f(-x)=-2f(x),即xf '(x)+2f(x)>0,所以当x>0时,g'(x)=2xf(x)+x2f '(x)=x[2f(x)+xf '(x)]>0,所以g(x)=x2f(x)在(0,+∞)上单调递增,易知g(x)的图象在R上连续,又g(x)为奇函数,所以g(x)为R上的增函数.由g(log3(x2-1))+g(-1)<0得g(log3(x2-1))<-g(-1)=g(1),所以log3(x2-1)<1,即0
8.e2x(答案不唯一) 解析由①知函数f(x)可以是指数函数,由②可知函数f(x)单调递增.设f(x)=ax(a>0),由f '(x)=axln a>ax,得a>e.满足题意的函数可以为f(x)=e2x.(注:底数大于e的指数函数均可.)
9.(0,+∞) 解析令g(x)=,因为f '(x)
10.(1)方案一 选条件①.
由题意得f '(x)=2x+.
由已知得f '(2)=2a,即=2a,解得a=4.
方案二 选条件②.
由题意得f '(x)=2x+.
因为直线x+y+1=0的斜率为-,所以f '(1)=2,即2+2a=2,解得a=0.
方案三 选条件③.
由题意得f '(x)=2x+.
因为直线4x-y=0的斜率为4,所以f '(1)=4,
即2+2a=4,解得a=1.
(2)由题意得g'(x)=-+2x+.
由函数g(x)在[1,2]上单调递减,可得g'(x)≤0在[1,2]上恒成立,即-+2x+≤0在[1,2]上恒成立,即a≤-x2在[1,2]上恒成立.
令h(x)=-x2,x∈[1,2],则h'(x)=--2x<0,即h(x)在[1,2]上单调递减,所以h(x)min=h(2)=-,
故a≤-,即实数a的取值范围为(-∞,-].
11.(1)因为a=1,所以f(x)=xex+x2+2x,
则f '(x)=ex+xex+2x+2=(x+1)(ex+2),
则f(-1)=-,f '(-1)=0,
故f(x)的图象在x=-1处的切线方程为y=-.
(2)f '(x)=(x+1)ex+2ax+2a=(x+1)(ex+2a).
若a≥0,则ex+2a>0恒成立,
所以当x∈(-∞,-1)时,f '(x)<0,函数f(x)单调递减;
当x∈(-1,+∞)时,f '(x)>0,函数f(x)单调递增.
若a<0,则由ex+2a=0,得x=ln(-2a).
当ln(-2a)<-1,即-
当ln(-2a)=-1,即a=-时,f '(x)≥0在R上恒成立,函数f(x)单调递增.
当ln(-2a)>-1,即a<-时,
若x∈(-∞,-1),则f '(x)>0,函数f(x)单调递增;若x∈(-1,ln(-2a)),则f '(x)<0,函数f(x)单调递减;若x∈(ln(-2a),+∞),则f '(x)>0,函数f(x)单调递增.
综上所述,当a≥0时,f(x)的单调递增区间为(-1,+∞),单调递减区间为(-∞,-1);
当-
当a<-时,f(x)的单调递增区间为(-∞,-1)和(ln(-2a),+∞),单调递减区间为(-1,ln(-2a)).
12.(1)由题意,得f(x)的定义域为(0,+∞),f '(x)=.
由y=x,y=ln x的图象(如图所示)可知,在(0,+∞)上x>ln x恒成立,所以f '(x)>0,
所以f(x)在(0,+∞)上单调递增.
(2)由(1)知f(x)在(0,+∞)上单调递增,故当x>1时,f(x)>f(1)=2,故 .
g'(x)=,因为x>1,所以1-ex<0,所以g'(x)<0,即g(x)在(1,+∞)上单调递减,
所以当x>1时,g(x)
13.(1)由题意得f '(x)=-2asin x+.
因为f '()=0,所以-2a+1=0,解得a=,
所以f '(x)=-sin x+.
令φ(x)=f '(x)=-sin x+,则φ'(x)=-cos x-,
当x∈(0,)时,φ'(x)<0,故f '(x)在(0,)上单调递减,
所以f '(x)>f '()=0,故f(x)在(0,)上单调递增.
(2)由(1)知f(x)=cos x-+1,
令h(x)=f(x)=(1+cos x)-1,
因为≠0,所以f(x)与h(x)有相同的零点个数,
h'(x)=(-sin x+1+cos x)=[1-sin(x-)],
当x∈[2kπ+,2kπ+π](k∈N)时,x-∈[2kπ+,2kπ+](k∈N),所以sin(x-)∈[,1],则sin(x-)∈[1,],故h'(x)≤0,所以h(x)在[2kπ+,2kπ+π](k∈N)上单调递减.
因为k∈N,h(2kπ+)=e2kπ-1≥0,h(2kπ+π)=-1<0,
所以由函数零点存在定理可知,h(x)在[2kπ+,2kπ+π](k∈N)上只有一个零点,
故函数f(x)在[2kπ+,2kπ+π](k∈N)上只有一个零点.
