2022-2023学年高一下学期物理人教版必修2 6.4万有引力的成就 课件 (共19张PPT)
文档属性
| 名称 | 2022-2023学年高一下学期物理人教版必修2 6.4万有引力的成就 课件 (共19张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 924.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2023-03-07 11:25:38 | ||
图片预览





文档简介
(共19张PPT)
4.万有引力理论的成就
第六章 万有引力与航天
阿基米德在研究杠杆原理后,曾经说过一句名言
“给我一个支点,我可以撬动地球。”
那我们又是怎么知道巨大的地球的质量的呢
那给我们一个杠杆(天平)是否就可以称量地球的质量了呢?
不可行
英国科学家卡文迪许
被称为第一个称出地球质量的人
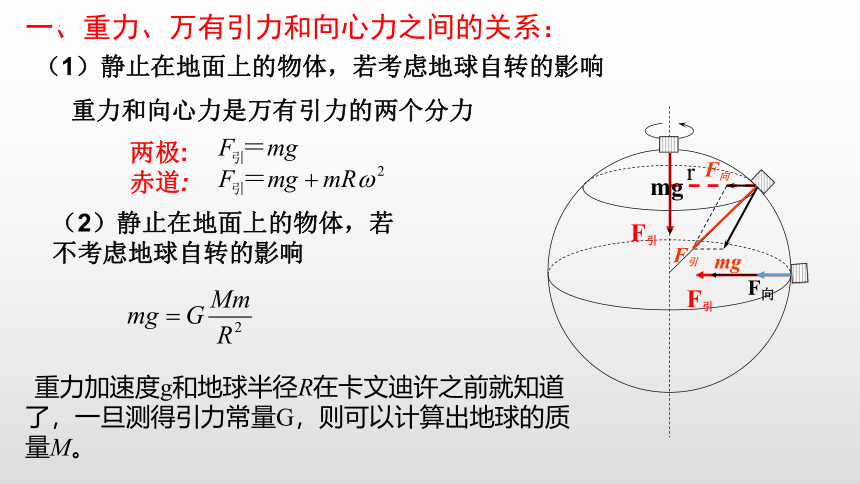
一、重力、万有引力和向心力之间的关系:
F引
mg
F向
F引
mg
F引
F向
r
两极: 赤道:
重力和向心力是万有引力的两个分力
(1)静止在地面上的物体,若考虑地球自转的影响
(2)静止在地面上的物体,若不考虑地球自转的影响
重力加速度g和地球半径R在卡文迪许之前就知道了,一旦测得引力常量G,则可以计算出地球的质量M。
已知:地球表面g=9.8m/s2,地球半径R=6400km,引力常量G=6.67×10-11Nm2/kg2。请你根据这些数据计算地球的质量。(计算结果保留一位有效数字)
“称量地球的质量”
M=6.0×1024kg
利用物体在天体(如地球)表面时受到的重力近似等于万有引力
于是有
卡文迪许被称为“第一个称量地球质量的人”!
二.计算天体的质量
方法1:代换法或g、R法 所选物体在天体表面
原理: 不考虑自转,物体在天体表面附近受到的重力等于万有引力
适用条件:星球自转可忽略,且已知星球表面的重力加速度g、星球的半径R和引力常量G。
g可以通过弹簧秤测已知质量的物体的重力、利用自由落体规律、平抛运动规律等方法求解
例1 一宇航员为了估测一星球的质量,他在该星球的表面做自由落体实验:让小球在离地面h高处自由下落,他测出经时间t小球落地,又已知该星球的半径为R,试估算该星球的质量。
分析:
质量为m的小球在星球表面
g =
小球自由下落
思考1:
测出某行星绕太阳的公转周期T、轨道半径r,能不能由此求出太阳的质量M?
分析:
1.将行星的运动看成是匀速圆周运动.
2.万有引力提供向心力 F引=Fn.
思考2:不同行星与太阳的距离r和绕太阳公转的周期T都是不同的,但是由不同行星的r、T计算出来的太阳质量必须是一样的!上面这个公式能保证这一点吗?
能,因为对同一中心天体r3/T2=k是相同的。
思考3 :用该方法能求出行星的质量吗?
只能求出中心天体的质量
要测量谁的质量就绕谁转——被测的是中心天体质量
例2 太阳光经500 s到达地球,地球的半径为6.4×106 m,表面的重力加速度为g=9.8 m/s2,光速c=3.0×108m/s,1年=3.2×107 s。试估算太阳质量(保留1位有效数字)。
地球到太阳的距离为r=ct=3.0×108×500 m=1.5×1011m ①
地球绕太阳的运动可看成是匀速圆周运动,
得太阳的质量为
代入数据得太阳的质量为M=2×1030kg
思考4:知道环绕体的线速度v或角速度ω及其轨道半径r,能不能求出中心天体的质量?
能。利用环绕天体,其所受的万有引力提供向心力F引= Fn
已知v和r
已知ω和r
已知T和r
方法2:环绕法 所选物体在中心天体上空
原理 行星(或卫星)做匀速圆周运动所需的万有引力提供向心力F引=Fn
适用条件:只能求出中心天体的质量!!!
根据上面两种方式算出中心天体的质量M,
结合球体体积计算公式
物体的密度计算公式
求出中心天体的密度
三.计算天体的平均密度
1.基本思路
2.天体密度的计算1—物体在天体表面
3.天体密度的计算2---卫星绕中心天体做匀速圆周运动
r≈R
当卫星中心天体表面运动时
只能求出中心天体的质量和密度!不能求出环绕天体的质量和密度!
例3:已知地球的一颗人造卫星的运行周期为 T 、轨道距地面高为 h ,地球的半径 R ,求地球的质量和密度?
解:
当卫星在行星表面做近地运行时即h≈0,可近似认为 R+h≈R
地球的体积
中心天体M
转动天体m
轨道半经r
明确各个物理量
天体半径R
针对练习
1、已知引力常量G和下列各组数据,能计算出地球质量的是( )
A.地球绕太阳运行的周期及地球离太阳的距离
B.月球绕地球运行的周期及月球离地球的距离
C.人造地球卫星在地面附近绕行的速度和运行周期
D.若不考虑地球自转,已知地球的半径及重力加速度
BCD
2.一艘宇宙飞船在一个星球表面附近作圆形轨道环绕飞行,宇航员要估测该星球的密度,只需要( )
A. 测定飞船的环绕半径 B. 测定行星的质量
C. 测定飞船的环绕周期 D. 测定飞船的环绕速度
C
四.发现未知天体
背景:1781年由英国物理学家威廉.赫歇尔发现了太阳系的第七颗行星—天王星,但观测到的天王星的运行轨迹与万有引力定律推测的结果有一些误差……
1、笔尖下发现的行星—海王星
2、预言实现—冥王星的发现
英国的剑桥大学的学生亚当斯和法国年轻的天文爱好者勒维耶
1930年3月14日,汤博发现了这颗新星——冥王星
新的天文发现不断使“九大行星”的传统观念受到质疑。天文学家先后发现冥王星与太阳系其他行星的一些不同之处。冥王星所处的轨道在海王星之外,属于太阳系外围的柯伊伯带,20世纪90年代以来,天文学家发现柯伊伯带有更多围绕太阳运行的大天体。国际天文学联合会大会通过的决议规定,“行星”指的是围绕太阳运转、自身引力足以克服其刚体力而使天体呈圆球状、能够清除其轨道附近其他物体的天体。在太阳系传统的“九大行星”中,只有水星、金星、地球、火星、木星、土星、天王星和海王星符合这些要求。冥王星由于其轨道与海王星的轨道相交,不符合新的行星定义,因此被自动降级为“矮行星”。
知识小拓展——冥王星的离开
一、两种基本运动情景
(1)地面上随地球自转的物体运动情景
(2)空中绕地球运动的卫星运动情景
θ
R
M
w
r
m
Fn
G
F引
忽略自转
F引 = mg
F引 = Fn
卫星
r
F引
小结
对天体表面的物体:
对环绕卫星:
卫星环绕周期
(1)求天体质量的方法:
(2)求天体的平均密度:
天体表面附近的卫星:
,
天体体半径
中心天体的质量
卫星轨道半径
r = R+h
二、两种基本应用
4.万有引力理论的成就
第六章 万有引力与航天
阿基米德在研究杠杆原理后,曾经说过一句名言
“给我一个支点,我可以撬动地球。”
那我们又是怎么知道巨大的地球的质量的呢
那给我们一个杠杆(天平)是否就可以称量地球的质量了呢?
不可行
英国科学家卡文迪许
被称为第一个称出地球质量的人
一、重力、万有引力和向心力之间的关系:
F引
mg
F向
F引
mg
F引
F向
r
两极: 赤道:
重力和向心力是万有引力的两个分力
(1)静止在地面上的物体,若考虑地球自转的影响
(2)静止在地面上的物体,若不考虑地球自转的影响
重力加速度g和地球半径R在卡文迪许之前就知道了,一旦测得引力常量G,则可以计算出地球的质量M。
已知:地球表面g=9.8m/s2,地球半径R=6400km,引力常量G=6.67×10-11Nm2/kg2。请你根据这些数据计算地球的质量。(计算结果保留一位有效数字)
“称量地球的质量”
M=6.0×1024kg
利用物体在天体(如地球)表面时受到的重力近似等于万有引力
于是有
卡文迪许被称为“第一个称量地球质量的人”!
二.计算天体的质量
方法1:代换法或g、R法 所选物体在天体表面
原理: 不考虑自转,物体在天体表面附近受到的重力等于万有引力
适用条件:星球自转可忽略,且已知星球表面的重力加速度g、星球的半径R和引力常量G。
g可以通过弹簧秤测已知质量的物体的重力、利用自由落体规律、平抛运动规律等方法求解
例1 一宇航员为了估测一星球的质量,他在该星球的表面做自由落体实验:让小球在离地面h高处自由下落,他测出经时间t小球落地,又已知该星球的半径为R,试估算该星球的质量。
分析:
质量为m的小球在星球表面
g =
小球自由下落
思考1:
测出某行星绕太阳的公转周期T、轨道半径r,能不能由此求出太阳的质量M?
分析:
1.将行星的运动看成是匀速圆周运动.
2.万有引力提供向心力 F引=Fn.
思考2:不同行星与太阳的距离r和绕太阳公转的周期T都是不同的,但是由不同行星的r、T计算出来的太阳质量必须是一样的!上面这个公式能保证这一点吗?
能,因为对同一中心天体r3/T2=k是相同的。
思考3 :用该方法能求出行星的质量吗?
只能求出中心天体的质量
要测量谁的质量就绕谁转——被测的是中心天体质量
例2 太阳光经500 s到达地球,地球的半径为6.4×106 m,表面的重力加速度为g=9.8 m/s2,光速c=3.0×108m/s,1年=3.2×107 s。试估算太阳质量(保留1位有效数字)。
地球到太阳的距离为r=ct=3.0×108×500 m=1.5×1011m ①
地球绕太阳的运动可看成是匀速圆周运动,
得太阳的质量为
代入数据得太阳的质量为M=2×1030kg
思考4:知道环绕体的线速度v或角速度ω及其轨道半径r,能不能求出中心天体的质量?
能。利用环绕天体,其所受的万有引力提供向心力F引= Fn
已知v和r
已知ω和r
已知T和r
方法2:环绕法 所选物体在中心天体上空
原理 行星(或卫星)做匀速圆周运动所需的万有引力提供向心力F引=Fn
适用条件:只能求出中心天体的质量!!!
根据上面两种方式算出中心天体的质量M,
结合球体体积计算公式
物体的密度计算公式
求出中心天体的密度
三.计算天体的平均密度
1.基本思路
2.天体密度的计算1—物体在天体表面
3.天体密度的计算2---卫星绕中心天体做匀速圆周运动
r≈R
当卫星中心天体表面运动时
只能求出中心天体的质量和密度!不能求出环绕天体的质量和密度!
例3:已知地球的一颗人造卫星的运行周期为 T 、轨道距地面高为 h ,地球的半径 R ,求地球的质量和密度?
解:
当卫星在行星表面做近地运行时即h≈0,可近似认为 R+h≈R
地球的体积
中心天体M
转动天体m
轨道半经r
明确各个物理量
天体半径R
针对练习
1、已知引力常量G和下列各组数据,能计算出地球质量的是( )
A.地球绕太阳运行的周期及地球离太阳的距离
B.月球绕地球运行的周期及月球离地球的距离
C.人造地球卫星在地面附近绕行的速度和运行周期
D.若不考虑地球自转,已知地球的半径及重力加速度
BCD
2.一艘宇宙飞船在一个星球表面附近作圆形轨道环绕飞行,宇航员要估测该星球的密度,只需要( )
A. 测定飞船的环绕半径 B. 测定行星的质量
C. 测定飞船的环绕周期 D. 测定飞船的环绕速度
C
四.发现未知天体
背景:1781年由英国物理学家威廉.赫歇尔发现了太阳系的第七颗行星—天王星,但观测到的天王星的运行轨迹与万有引力定律推测的结果有一些误差……
1、笔尖下发现的行星—海王星
2、预言实现—冥王星的发现
英国的剑桥大学的学生亚当斯和法国年轻的天文爱好者勒维耶
1930年3月14日,汤博发现了这颗新星——冥王星
新的天文发现不断使“九大行星”的传统观念受到质疑。天文学家先后发现冥王星与太阳系其他行星的一些不同之处。冥王星所处的轨道在海王星之外,属于太阳系外围的柯伊伯带,20世纪90年代以来,天文学家发现柯伊伯带有更多围绕太阳运行的大天体。国际天文学联合会大会通过的决议规定,“行星”指的是围绕太阳运转、自身引力足以克服其刚体力而使天体呈圆球状、能够清除其轨道附近其他物体的天体。在太阳系传统的“九大行星”中,只有水星、金星、地球、火星、木星、土星、天王星和海王星符合这些要求。冥王星由于其轨道与海王星的轨道相交,不符合新的行星定义,因此被自动降级为“矮行星”。
知识小拓展——冥王星的离开
一、两种基本运动情景
(1)地面上随地球自转的物体运动情景
(2)空中绕地球运动的卫星运动情景
θ
R
M
w
r
m
Fn
G
F引
忽略自转
F引 = mg
F引 = Fn
卫星
r
F引
小结
对天体表面的物体:
对环绕卫星:
卫星环绕周期
(1)求天体质量的方法:
(2)求天体的平均密度:
天体表面附近的卫星:
,
天体体半径
中心天体的质量
卫星轨道半径
r = R+h
二、两种基本应用
