苏教版六年级下册数学作业课件 第六单元 (共28张PPT)
文档属性
| 名称 | 苏教版六年级下册数学作业课件 第六单元 (共28张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-07 00:00:00 | ||
图片预览






文档简介
(共28张PPT)
第六单元
六 正比例和反比例
第1课时 正比例的意义
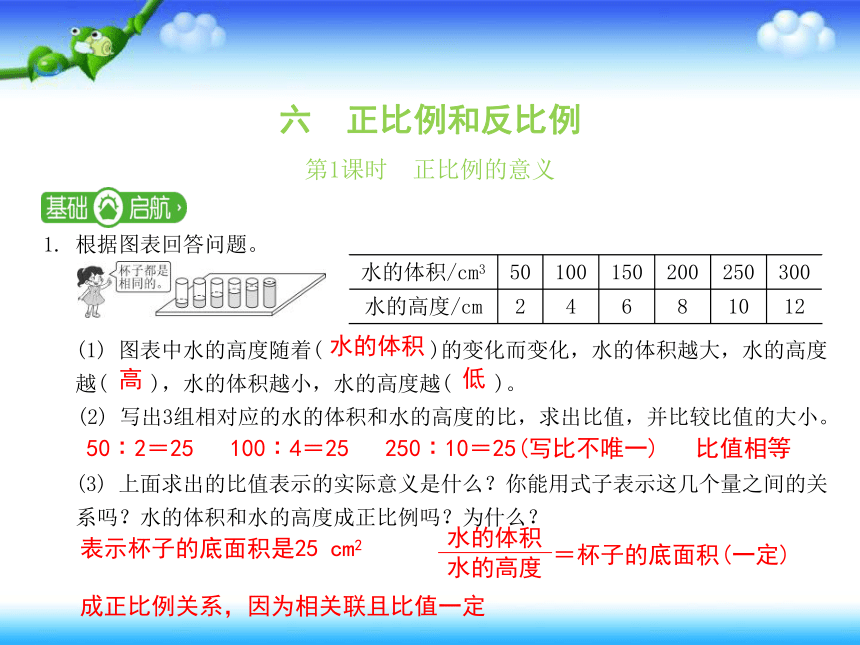
1. 根据图表回答问题。
(1) 图表中水的高度随着( )的变化而变化,水的体积越大,水的高度
越( ),水的体积越小,水的高度越( )。
(2) 写出3组相对应的水的体积和水的高度的比,求出比值,并比较比值的大小。
(3) 上面求出的比值表示的实际意义是什么?你能用式子表示这几个量之间的关
系吗?水的体积和水的高度成正比例吗?为什么?
水的体积/cm3 50 100 150 200 250 300
水的高度/cm 2 4 6 8 10 12
水的体积
高
低
50∶2=25 100∶4=25 250∶10=25(写比不唯一) 比值相等
表示杯子的底面积是25 cm2
水的体积
水的高度
=杯子的底面积(一定)
成正比例关系,因为相关联且比值一定
2. 填空。
(1) =( ),当( )一定时,( )和( )成正比例。
(2) =分数值,当( )一定时,( )和( )成正比例。
(3) =k(x≠0),当( )一定时,( )和( )成正比例。
(4) 对于小学生的身高和年龄,虽然身高基本随着年龄的增长而( ),但
( )与( )的比的比值( ),所以小学生的身高和年龄( )
正比例。
总价
数量
( )
( )
单价
单价
总价
数量
分数值
分子
分母
分子
分母
k
y
x
增高
身高
年龄
不一定
不成
3. 判断下面每题中的两种量是否成正比例。(在括号里填“是”或“否”)
(1) 工作效率一定,工作时间和工作总量。 ( )
(2) 比例尺一定,图上距离和实际距离。 ( )
(3) 速度一定,路程和时间。 ( )
(4) 购买练习本的数量和总价。 ( )
(5) 分数的分母一定,分子和分数值(分子和分数值均不为0)。 ( )
(6) 两个不为0的因数,一个因数不变,另一个因数和积。 ( )
4. 判断下面各题中的x和y是否成正比例。(x、y均不为0,在括号里填“是”或
“否”)
(1) 4x=9y( ) (2) =10y( )
(3) x-y=0( ) (4) x-y=0.9( )
是
是
是
否
是
是
是
否
是
否
5. 先分别按1∶4和1∶2的比画出圆缩小后的图形,再填写下面的表格,并回答问题。
(得数保留π)
圆的周长和半径成正比例吗?圆的面积和半径成正比例吗?为什么?
圆的半径/厘米 1 2 4
圆的周长/厘米
圆的面积/平方厘米
图略 圆的周长和半径成正比例,因为它们的比值一定,是2π;圆的面积和半径不成正比例,因为它们的比值不同 解析:先完成表格,再看对应量的比值是否相等,是就成正比例,否则不成正比例。
2π
4π
8π
π
4π
16π
第2课时 正比例图像
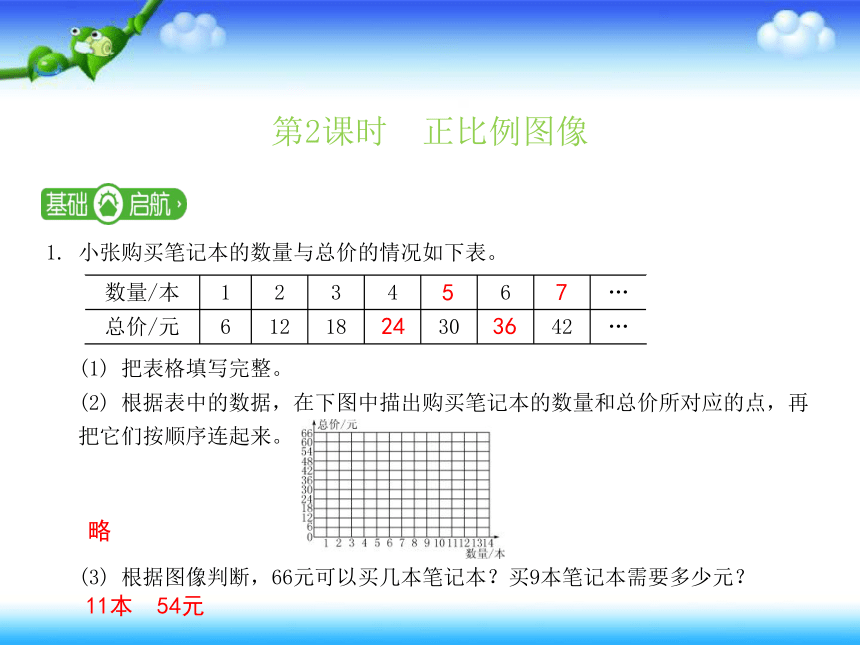
1. 小张购买笔记本的数量与总价的情况如下表。
(1) 把表格填写完整。
(2) 根据表中的数据,在下图中描出购买笔记本的数量和总价所对应的点,再
把它们按顺序连起来。
(3) 根据图像判断,66元可以买几本笔记本?买9本笔记本需要多少元?
数量/本 1 2 3 4 6 …
总价/元 6 12 18 30 42 …
11本 54元
略
24
5
36
7
2. 某一天的某一时刻,淘淘测量了几个不同物体的高度和影长。
(1) 根据上图判断,在这一时刻,物体的高度与影长成什么关系?
(2) 根据图像判断如果一个物体的影长是6分米,这个物体的高是多少分米?
正比例关系
10分米
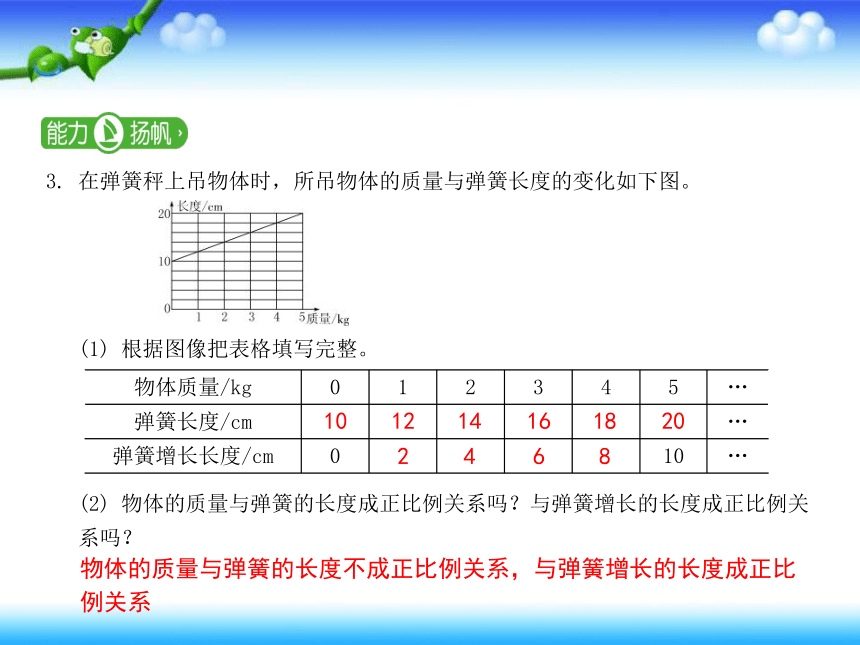
3. 在弹簧秤上吊物体时,所吊物体的质量与弹簧长度的变化如下图。
(1) 根据图像把表格填写完整。
(2) 物体的质量与弹簧的长度成正比例关系吗?与弹簧增长的长度成正比例关
系吗?
物体质量/kg 0 1 2 3 4 5 …
弹簧长度/cm …
弹簧增长长度/cm 0 10 …
物体的质量与弹簧的长度不成正比例关系,与弹簧增长的长度成正比
例关系
10
12
14
16
18
20
2
4
6
8
4. 甲、乙两车的行驶情况如下图。(甲、乙两车同时同地向相同方向出发)
(1) 甲、乙两车行驶的路程和时间成正比例关系吗?
(2) 根据图像判断,乙行640千米需要几小时?8小时时甲在乙的前面多远处?
成正比例关系
8小时 160千米
5. 根据上面第4题的图像思考,如果甲、乙两车同时从相距 800千米的两地相向而
行,几小时相遇?
800÷(160÷2+400÷4)=4(小时) 解析:先从图像中发现乙2小时行160千米,甲4小时行400千米,然后求出速度再解答,解答此题时还可以将甲的图像倒过来画,寻找交叉点。
第3课时 反比例的意义
1. 根据图表回答问题。
(1) 图表中水的高度随着( )的变化而变化,杯子的底面积越小,
水的高度越( ),杯子的底面积越大,水的高度越( )。
(2) 水的底面积和水的高度成什么比例?为什么?
杯子的底面积/cm2 10 15 20 30 60
水的高度/cm 30 20 15 10 5
杯子的底面积
高
低
成反比例,因为相关联,且积是定值
2. (1) 修路队修一条公路,每天修的长度和修的时间如下表,根据表中的数据回答
下面的问题。
修路队每天修的长度和修的时间成反比例吗?为什么?
(2) 修路队修一条公路,已修的长度和剩下的长度如下表,根据表中的数据回答
下面的问题。
已修的长度和剩下的长度成反比例吗?为什么?
每天修的长度/米 480 120 96 48
修的时间/天 2 8 10 20
已修的长度/米 100 200 300 400
剩下的长度/米 500 400 300 200
成反比例,因为相关联,且积是定值
不成反比例,因为他们的积不是定值
3. 下表中A和B是两种相关联的量,先根据表中四组已知数据判断它们成什么比例关
系,再把表格填完整。
A与B的( )一定,因此A与B成( )比例。
A 1 2 3 4 6 …
B 36 18 12 9 4 …
积
反
6
9
4. 判断下面每题中两种相关联的量是否成反比例。(在括号里填“是”或“否”)
(1) 图上距离一定,实际距离和比例尺。 ( )
(2) 和一定,一个加数与另一个加数。 ( )
(3) 铺地面积一定,方砖边长与所需方砖的数量。 ( )
(4) 圆的周长一定,圆周率和直径。 ( )
是
否
否
否
5. 看图填表,回答问题。
三角形的面积一定,底和高成反比例吗?为什么?
① ② ③
面积/cm2
底/cm
高/cm
成反比例,因为三角形的底和高的积一定
4
2
4
4
8
1
4
4
2
6. 根据下图中的图像和已知数据判断,图中速度和时间成反比例关系吗?为什么?
正比例图像和反比例图像有什么不同?
成反比例关系 因为1×100=100(千米),2×50=100(千米),4×
25=100(千米)……速度×时间=路程(一定) 答案不唯一,如正比例图像是一条直线,反比例图像是一条曲线 解析:先计算两个量的积,再根据积判断是否成反比例。正比例图像和反比例图像明显不同,一个是直线,一个是曲线。(答案不唯一)
第4课时 练 习 课
1. 填空。
(1) 在每块瓷砖的面积、瓷砖的数量和总面积三个量中:
① 当每块瓷砖的面积一定时,( )和( )成( )比例;
② 当瓷砖的数量一定时,( )和( )成( )比例;
③ 当总面积一定时,( )和( )成( )比例。
(2) M和N是两种相关联的量,a、b、c、d(都不为0)是它们其中的两组相对应的
值,如下表:
① 若a∶c=b∶d,则M和N成( )比例。
② 若a×c=b×d,则M和N成( )比例。
③ 已知a=12,b=6,c=4, 若M和N成正比例,则d=( ),若M和N成反比例,
则d=( )。
M a b …
N c d …
总面积
瓷砖的数量
正
总面积
每块瓷砖的面积
正
每块瓷砖的面积
瓷砖的数量
反
正
反
2
8
2. 判断。
(1) 圆的面积和半径成正比例。 ( )
(2) 在不同的地图上,南京到北京的图上距离和相对应的比例尺成正比例。
( )
(3) 利率和存期一定,存入银行的本金和利息成正比例。 ( )
(4) 总路程一定,已行的路程和剩下的路程成反比例。 ( )
(5) 因为y=,所以x和y成反比例。 ( )
(6) 零件的总数量一定,做一个零件用的时间和总时间成正比例。 ( )
(7) 两个互相咬合的齿轮,齿轮的齿数和转数成反比例。 ( )
×
√
√
×
√
√
√
3. 选择。
(1) 王师傅一天工作8小时,他做一个零件所用的时间和一天所做的零件数量
( )。
① 成正比例 ② 成反比例 ③ 不成比例
(2) 全班人数一定,出勤人数和出勤率( )。
① 成正比例 ② 成反比例 ③ 不成比例
(3) 把64升水倒入一个长方体容器内,水面的高度和容器内部的底面积( )。
① 成正比例 ② 成反比例 ③ 不成比例
(4) =y(x、y均不为0),那么x和y( )。
① 成正比例 ② 成反比例 ③ 不成比例
②
①
②
①
4. 在同一时刻,同一地点,刘涛量得学校里旗杆的影长是36米,妹妹的影长是1.8
米。你知道旗杆高多少米吗?
5. 小明发现他的自行车前齿轮有50个齿,后齿轮有20个齿,前齿轮转一圈,后齿轮
转几圈?
50÷20=2.5(圈) 12×2.5=30(圈)
设旗杆高x米。 1.8∶1.5=36∶x x=30
6. 下图是一个杠杆,想一想,要使下面的杠杆保持平衡,右侧的托盘里应该放入多
少个同样的三角形物体? (要使杠杆保持平衡,则要使两边物体的质量与物体到
支点0的水平距离的乘积相等)
设右侧的托盘里应该放入x个同样的三角形物体。
2×x=3×4 x=6 解析:可以根据题目括号中的原理列方程求解。
满分:100分 时间:60分钟 得分:_____
第六单元自主检测
一、填空。(每空2分,共24分)
1. 已知A÷B=C(B≠0),当A一定时,B和C成( )比例;当B一定时,A和C成( )
比例;当C一定时,A和B成( )比例。
2. 包装一批糖果,( )一定时,每袋所装千克数和( )成反比例。
3. 输液时药水的体积一定,每分钟滴的滴数与输液时间成( )比例。
4. 如果长方体的底面积不变,那么它的体积和高成( )比例。
5. 如果x=,那么x和y成( )比例;如果=,那么x和y成( )比例。
6. 下表中,如果x和y成正比例,那么空格里应填( );如果x和y成反比例,那么
空格里应填( )。
x 2 6
y 24
反
正
正
糖果总质量
装的袋数
反
正
正
反
72
8
7. 如右图,一个大长方形被分成了四个小长方形,已知三个长方形的
面积,阴影部分的面积是( )。
二、判断。(每题2分,共14分)
1. 两种相关联的量,不是成正比例就是成反比例。 ( )
2. 正方形的面积和边长成正比例。 ( )
3. 因为3A=4B(A、B均不为0),所以A和B成正比例。 ( )
4. 400米赛跑,运动员的平均速度和所用的时间成反比例。 ( )
5. 圆的周长和它的半径成正比例。 ( )
6. 一个不为0的数和它的倒数成反比例。 ( )
7. 老王工作的时间和他加工产品的数量成正比例。 ( )
三、选择。(每空2分,共16分)
1. 双“十一”时超市里某食品全部6折酬宾,购买该食品的现价和原价( )。
① 成正比例 ② 成反比例 ③ 不成比例
12 m2
×
×
√
√
√
√
×
①
2. 王师傅一天织布6小时,他织1米布所用的时间和一天织布的总数量( )。
① 成正比例 ② 成反比例 ③ 不成比例
3. 梯形的面积一定,梯形的上、下底之和与高( )。
① 成正比例 ② 成反比例 ③ 不成比例
4. 下面表示x和y成反比例的式子是( )。
① y+x=10 ② y=0.6∶x ③ =x
5. 下面各选项中,( )成正比例,( )成反比例,( )不成比例。
① 比的前项一定,比的后项和比值 ② 分数值一定,分子和分母
③ 三角形的底和面积
6. 下面各选项中,两种量成反比例关系的是( )。
① 2.5升可乐,喝去的体积和剩下的体积
② 在C=2πr中,C一定,π和r
③ 路程一定,速度和时间
②
②
②
②
①
③
③
四、解比例。(共12分)
2.5∶x=0.5∶10 5∶8=8∶x
∶=x∶ x∶=∶
x=50
x=12.8
x=1
x=
五、解决问题。(共34分)
1. 下面的图像表示的是某汽车车轮转的圈数和所行路程的关系。
(1) 看图填写下表。(2分)
(2) 这辆汽车所行的路程和车轮转的圈数成比例吗?如果成,那么成什么比例?
为什么?(4分)
圈 数 1 2 5 7
路程/米 3.14 9.42 18.84
汽车所行的路程和车轮转的圈数成比例,成正比例,因为它们的比值一定
6.28
15.7
21.98
3
6
2. 四名同学到超市购买练习本。填表,并回答问题。
(1) 如果他们都花了24元,买不同的练习本,练习本的单价和购买的数量成什么
比例?为什么?(3分)
(2) 如果他们都买单价是2元/本的练习本,购买的数量和总价成什么比例?为什
么?(3分)
张 华 李 浩 王 佟 陈 刚
单价/(元/本) 1 1.2 3 4
数量/本
张 华 李 浩 王 佟 陈 刚
数量/本 2 5 8 9
总价/元
成反比例关系,因为单价×数量=总价(一定)
成正比例关系,因为 =单价(一定)
总价
数量
24
20
8
6
4
10
16
18
(3) 如果他们都带了24元,那么买练习本用去的钱数和剩下的钱数成比例吗?为什么?(3分)
张 华 李 浩 王 佟 陈 刚
用去/元 2.4 8 12 20
剩下/元
21.6
16
12
4
不成比例,因为两个量的积和比值不一定
3. 一箱啤酒12瓶。
(1) 填写上表,在下图中描出箱数和瓶数对应的点,再把它们按顺序连起来。
(2分)
(2) 啤酒的瓶数和箱数成什么比例?为什么?(2分)
(3) 8箱啤酒有多少瓶?144瓶啤酒可以装多少箱?(3分)
箱 数 1 2 3 4 5 …
瓶 数 …
12
24
36
48
60
图略
啤酒的瓶数和箱数成正比例,因为它们的比值一定
12×8=96(瓶) 144÷12=12(箱)
4. 一台磨粉机5小时磨面粉450千克,照这样计算,磨270千克面粉需要几小时?(4
分)
5. 一间房间用面积是16平方分米的方砖铺需要100块,改用边长为5分米的方砖铺需
要多少块?(4分)
6. 同一时刻测得大树影长和木桩高度及影长,这棵大树有多高?(4分)
设大树高x米。
1.5∶1.2=x∶3.6
x=4.5
270÷(450÷5)=3(小时)
16×100÷(5×5)=64(块)
第六单元
六 正比例和反比例
第1课时 正比例的意义
1. 根据图表回答问题。
(1) 图表中水的高度随着( )的变化而变化,水的体积越大,水的高度
越( ),水的体积越小,水的高度越( )。
(2) 写出3组相对应的水的体积和水的高度的比,求出比值,并比较比值的大小。
(3) 上面求出的比值表示的实际意义是什么?你能用式子表示这几个量之间的关
系吗?水的体积和水的高度成正比例吗?为什么?
水的体积/cm3 50 100 150 200 250 300
水的高度/cm 2 4 6 8 10 12
水的体积
高
低
50∶2=25 100∶4=25 250∶10=25(写比不唯一) 比值相等
表示杯子的底面积是25 cm2
水的体积
水的高度
=杯子的底面积(一定)
成正比例关系,因为相关联且比值一定
2. 填空。
(1) =( ),当( )一定时,( )和( )成正比例。
(2) =分数值,当( )一定时,( )和( )成正比例。
(3) =k(x≠0),当( )一定时,( )和( )成正比例。
(4) 对于小学生的身高和年龄,虽然身高基本随着年龄的增长而( ),但
( )与( )的比的比值( ),所以小学生的身高和年龄( )
正比例。
总价
数量
( )
( )
单价
单价
总价
数量
分数值
分子
分母
分子
分母
k
y
x
增高
身高
年龄
不一定
不成
3. 判断下面每题中的两种量是否成正比例。(在括号里填“是”或“否”)
(1) 工作效率一定,工作时间和工作总量。 ( )
(2) 比例尺一定,图上距离和实际距离。 ( )
(3) 速度一定,路程和时间。 ( )
(4) 购买练习本的数量和总价。 ( )
(5) 分数的分母一定,分子和分数值(分子和分数值均不为0)。 ( )
(6) 两个不为0的因数,一个因数不变,另一个因数和积。 ( )
4. 判断下面各题中的x和y是否成正比例。(x、y均不为0,在括号里填“是”或
“否”)
(1) 4x=9y( ) (2) =10y( )
(3) x-y=0( ) (4) x-y=0.9( )
是
是
是
否
是
是
是
否
是
否
5. 先分别按1∶4和1∶2的比画出圆缩小后的图形,再填写下面的表格,并回答问题。
(得数保留π)
圆的周长和半径成正比例吗?圆的面积和半径成正比例吗?为什么?
圆的半径/厘米 1 2 4
圆的周长/厘米
圆的面积/平方厘米
图略 圆的周长和半径成正比例,因为它们的比值一定,是2π;圆的面积和半径不成正比例,因为它们的比值不同 解析:先完成表格,再看对应量的比值是否相等,是就成正比例,否则不成正比例。
2π
4π
8π
π
4π
16π
第2课时 正比例图像
1. 小张购买笔记本的数量与总价的情况如下表。
(1) 把表格填写完整。
(2) 根据表中的数据,在下图中描出购买笔记本的数量和总价所对应的点,再
把它们按顺序连起来。
(3) 根据图像判断,66元可以买几本笔记本?买9本笔记本需要多少元?
数量/本 1 2 3 4 6 …
总价/元 6 12 18 30 42 …
11本 54元
略
24
5
36
7
2. 某一天的某一时刻,淘淘测量了几个不同物体的高度和影长。
(1) 根据上图判断,在这一时刻,物体的高度与影长成什么关系?
(2) 根据图像判断如果一个物体的影长是6分米,这个物体的高是多少分米?
正比例关系
10分米
3. 在弹簧秤上吊物体时,所吊物体的质量与弹簧长度的变化如下图。
(1) 根据图像把表格填写完整。
(2) 物体的质量与弹簧的长度成正比例关系吗?与弹簧增长的长度成正比例关
系吗?
物体质量/kg 0 1 2 3 4 5 …
弹簧长度/cm …
弹簧增长长度/cm 0 10 …
物体的质量与弹簧的长度不成正比例关系,与弹簧增长的长度成正比
例关系
10
12
14
16
18
20
2
4
6
8
4. 甲、乙两车的行驶情况如下图。(甲、乙两车同时同地向相同方向出发)
(1) 甲、乙两车行驶的路程和时间成正比例关系吗?
(2) 根据图像判断,乙行640千米需要几小时?8小时时甲在乙的前面多远处?
成正比例关系
8小时 160千米
5. 根据上面第4题的图像思考,如果甲、乙两车同时从相距 800千米的两地相向而
行,几小时相遇?
800÷(160÷2+400÷4)=4(小时) 解析:先从图像中发现乙2小时行160千米,甲4小时行400千米,然后求出速度再解答,解答此题时还可以将甲的图像倒过来画,寻找交叉点。
第3课时 反比例的意义
1. 根据图表回答问题。
(1) 图表中水的高度随着( )的变化而变化,杯子的底面积越小,
水的高度越( ),杯子的底面积越大,水的高度越( )。
(2) 水的底面积和水的高度成什么比例?为什么?
杯子的底面积/cm2 10 15 20 30 60
水的高度/cm 30 20 15 10 5
杯子的底面积
高
低
成反比例,因为相关联,且积是定值
2. (1) 修路队修一条公路,每天修的长度和修的时间如下表,根据表中的数据回答
下面的问题。
修路队每天修的长度和修的时间成反比例吗?为什么?
(2) 修路队修一条公路,已修的长度和剩下的长度如下表,根据表中的数据回答
下面的问题。
已修的长度和剩下的长度成反比例吗?为什么?
每天修的长度/米 480 120 96 48
修的时间/天 2 8 10 20
已修的长度/米 100 200 300 400
剩下的长度/米 500 400 300 200
成反比例,因为相关联,且积是定值
不成反比例,因为他们的积不是定值
3. 下表中A和B是两种相关联的量,先根据表中四组已知数据判断它们成什么比例关
系,再把表格填完整。
A与B的( )一定,因此A与B成( )比例。
A 1 2 3 4 6 …
B 36 18 12 9 4 …
积
反
6
9
4. 判断下面每题中两种相关联的量是否成反比例。(在括号里填“是”或“否”)
(1) 图上距离一定,实际距离和比例尺。 ( )
(2) 和一定,一个加数与另一个加数。 ( )
(3) 铺地面积一定,方砖边长与所需方砖的数量。 ( )
(4) 圆的周长一定,圆周率和直径。 ( )
是
否
否
否
5. 看图填表,回答问题。
三角形的面积一定,底和高成反比例吗?为什么?
① ② ③
面积/cm2
底/cm
高/cm
成反比例,因为三角形的底和高的积一定
4
2
4
4
8
1
4
4
2
6. 根据下图中的图像和已知数据判断,图中速度和时间成反比例关系吗?为什么?
正比例图像和反比例图像有什么不同?
成反比例关系 因为1×100=100(千米),2×50=100(千米),4×
25=100(千米)……速度×时间=路程(一定) 答案不唯一,如正比例图像是一条直线,反比例图像是一条曲线 解析:先计算两个量的积,再根据积判断是否成反比例。正比例图像和反比例图像明显不同,一个是直线,一个是曲线。(答案不唯一)
第4课时 练 习 课
1. 填空。
(1) 在每块瓷砖的面积、瓷砖的数量和总面积三个量中:
① 当每块瓷砖的面积一定时,( )和( )成( )比例;
② 当瓷砖的数量一定时,( )和( )成( )比例;
③ 当总面积一定时,( )和( )成( )比例。
(2) M和N是两种相关联的量,a、b、c、d(都不为0)是它们其中的两组相对应的
值,如下表:
① 若a∶c=b∶d,则M和N成( )比例。
② 若a×c=b×d,则M和N成( )比例。
③ 已知a=12,b=6,c=4, 若M和N成正比例,则d=( ),若M和N成反比例,
则d=( )。
M a b …
N c d …
总面积
瓷砖的数量
正
总面积
每块瓷砖的面积
正
每块瓷砖的面积
瓷砖的数量
反
正
反
2
8
2. 判断。
(1) 圆的面积和半径成正比例。 ( )
(2) 在不同的地图上,南京到北京的图上距离和相对应的比例尺成正比例。
( )
(3) 利率和存期一定,存入银行的本金和利息成正比例。 ( )
(4) 总路程一定,已行的路程和剩下的路程成反比例。 ( )
(5) 因为y=,所以x和y成反比例。 ( )
(6) 零件的总数量一定,做一个零件用的时间和总时间成正比例。 ( )
(7) 两个互相咬合的齿轮,齿轮的齿数和转数成反比例。 ( )
×
√
√
×
√
√
√
3. 选择。
(1) 王师傅一天工作8小时,他做一个零件所用的时间和一天所做的零件数量
( )。
① 成正比例 ② 成反比例 ③ 不成比例
(2) 全班人数一定,出勤人数和出勤率( )。
① 成正比例 ② 成反比例 ③ 不成比例
(3) 把64升水倒入一个长方体容器内,水面的高度和容器内部的底面积( )。
① 成正比例 ② 成反比例 ③ 不成比例
(4) =y(x、y均不为0),那么x和y( )。
① 成正比例 ② 成反比例 ③ 不成比例
②
①
②
①
4. 在同一时刻,同一地点,刘涛量得学校里旗杆的影长是36米,妹妹的影长是1.8
米。你知道旗杆高多少米吗?
5. 小明发现他的自行车前齿轮有50个齿,后齿轮有20个齿,前齿轮转一圈,后齿轮
转几圈?
50÷20=2.5(圈) 12×2.5=30(圈)
设旗杆高x米。 1.8∶1.5=36∶x x=30
6. 下图是一个杠杆,想一想,要使下面的杠杆保持平衡,右侧的托盘里应该放入多
少个同样的三角形物体? (要使杠杆保持平衡,则要使两边物体的质量与物体到
支点0的水平距离的乘积相等)
设右侧的托盘里应该放入x个同样的三角形物体。
2×x=3×4 x=6 解析:可以根据题目括号中的原理列方程求解。
满分:100分 时间:60分钟 得分:_____
第六单元自主检测
一、填空。(每空2分,共24分)
1. 已知A÷B=C(B≠0),当A一定时,B和C成( )比例;当B一定时,A和C成( )
比例;当C一定时,A和B成( )比例。
2. 包装一批糖果,( )一定时,每袋所装千克数和( )成反比例。
3. 输液时药水的体积一定,每分钟滴的滴数与输液时间成( )比例。
4. 如果长方体的底面积不变,那么它的体积和高成( )比例。
5. 如果x=,那么x和y成( )比例;如果=,那么x和y成( )比例。
6. 下表中,如果x和y成正比例,那么空格里应填( );如果x和y成反比例,那么
空格里应填( )。
x 2 6
y 24
反
正
正
糖果总质量
装的袋数
反
正
正
反
72
8
7. 如右图,一个大长方形被分成了四个小长方形,已知三个长方形的
面积,阴影部分的面积是( )。
二、判断。(每题2分,共14分)
1. 两种相关联的量,不是成正比例就是成反比例。 ( )
2. 正方形的面积和边长成正比例。 ( )
3. 因为3A=4B(A、B均不为0),所以A和B成正比例。 ( )
4. 400米赛跑,运动员的平均速度和所用的时间成反比例。 ( )
5. 圆的周长和它的半径成正比例。 ( )
6. 一个不为0的数和它的倒数成反比例。 ( )
7. 老王工作的时间和他加工产品的数量成正比例。 ( )
三、选择。(每空2分,共16分)
1. 双“十一”时超市里某食品全部6折酬宾,购买该食品的现价和原价( )。
① 成正比例 ② 成反比例 ③ 不成比例
12 m2
×
×
√
√
√
√
×
①
2. 王师傅一天织布6小时,他织1米布所用的时间和一天织布的总数量( )。
① 成正比例 ② 成反比例 ③ 不成比例
3. 梯形的面积一定,梯形的上、下底之和与高( )。
① 成正比例 ② 成反比例 ③ 不成比例
4. 下面表示x和y成反比例的式子是( )。
① y+x=10 ② y=0.6∶x ③ =x
5. 下面各选项中,( )成正比例,( )成反比例,( )不成比例。
① 比的前项一定,比的后项和比值 ② 分数值一定,分子和分母
③ 三角形的底和面积
6. 下面各选项中,两种量成反比例关系的是( )。
① 2.5升可乐,喝去的体积和剩下的体积
② 在C=2πr中,C一定,π和r
③ 路程一定,速度和时间
②
②
②
②
①
③
③
四、解比例。(共12分)
2.5∶x=0.5∶10 5∶8=8∶x
∶=x∶ x∶=∶
x=50
x=12.8
x=1
x=
五、解决问题。(共34分)
1. 下面的图像表示的是某汽车车轮转的圈数和所行路程的关系。
(1) 看图填写下表。(2分)
(2) 这辆汽车所行的路程和车轮转的圈数成比例吗?如果成,那么成什么比例?
为什么?(4分)
圈 数 1 2 5 7
路程/米 3.14 9.42 18.84
汽车所行的路程和车轮转的圈数成比例,成正比例,因为它们的比值一定
6.28
15.7
21.98
3
6
2. 四名同学到超市购买练习本。填表,并回答问题。
(1) 如果他们都花了24元,买不同的练习本,练习本的单价和购买的数量成什么
比例?为什么?(3分)
(2) 如果他们都买单价是2元/本的练习本,购买的数量和总价成什么比例?为什
么?(3分)
张 华 李 浩 王 佟 陈 刚
单价/(元/本) 1 1.2 3 4
数量/本
张 华 李 浩 王 佟 陈 刚
数量/本 2 5 8 9
总价/元
成反比例关系,因为单价×数量=总价(一定)
成正比例关系,因为 =单价(一定)
总价
数量
24
20
8
6
4
10
16
18
(3) 如果他们都带了24元,那么买练习本用去的钱数和剩下的钱数成比例吗?为什么?(3分)
张 华 李 浩 王 佟 陈 刚
用去/元 2.4 8 12 20
剩下/元
21.6
16
12
4
不成比例,因为两个量的积和比值不一定
3. 一箱啤酒12瓶。
(1) 填写上表,在下图中描出箱数和瓶数对应的点,再把它们按顺序连起来。
(2分)
(2) 啤酒的瓶数和箱数成什么比例?为什么?(2分)
(3) 8箱啤酒有多少瓶?144瓶啤酒可以装多少箱?(3分)
箱 数 1 2 3 4 5 …
瓶 数 …
12
24
36
48
60
图略
啤酒的瓶数和箱数成正比例,因为它们的比值一定
12×8=96(瓶) 144÷12=12(箱)
4. 一台磨粉机5小时磨面粉450千克,照这样计算,磨270千克面粉需要几小时?(4
分)
5. 一间房间用面积是16平方分米的方砖铺需要100块,改用边长为5分米的方砖铺需
要多少块?(4分)
6. 同一时刻测得大树影长和木桩高度及影长,这棵大树有多高?(4分)
设大树高x米。
1.5∶1.2=x∶3.6
x=4.5
270÷(450÷5)=3(小时)
16×100÷(5×5)=64(块)
