北师大版(2019)必修第二册 同步试题 第6章 6-2 柱、锥、台的体积(含解析)
文档属性
| 名称 | 北师大版(2019)必修第二册 同步试题 第6章 6-2 柱、锥、台的体积(含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 527.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-07 09:19:03 | ||
图片预览


文档简介
6.2 柱、锥、台的体积
必备知识基础练
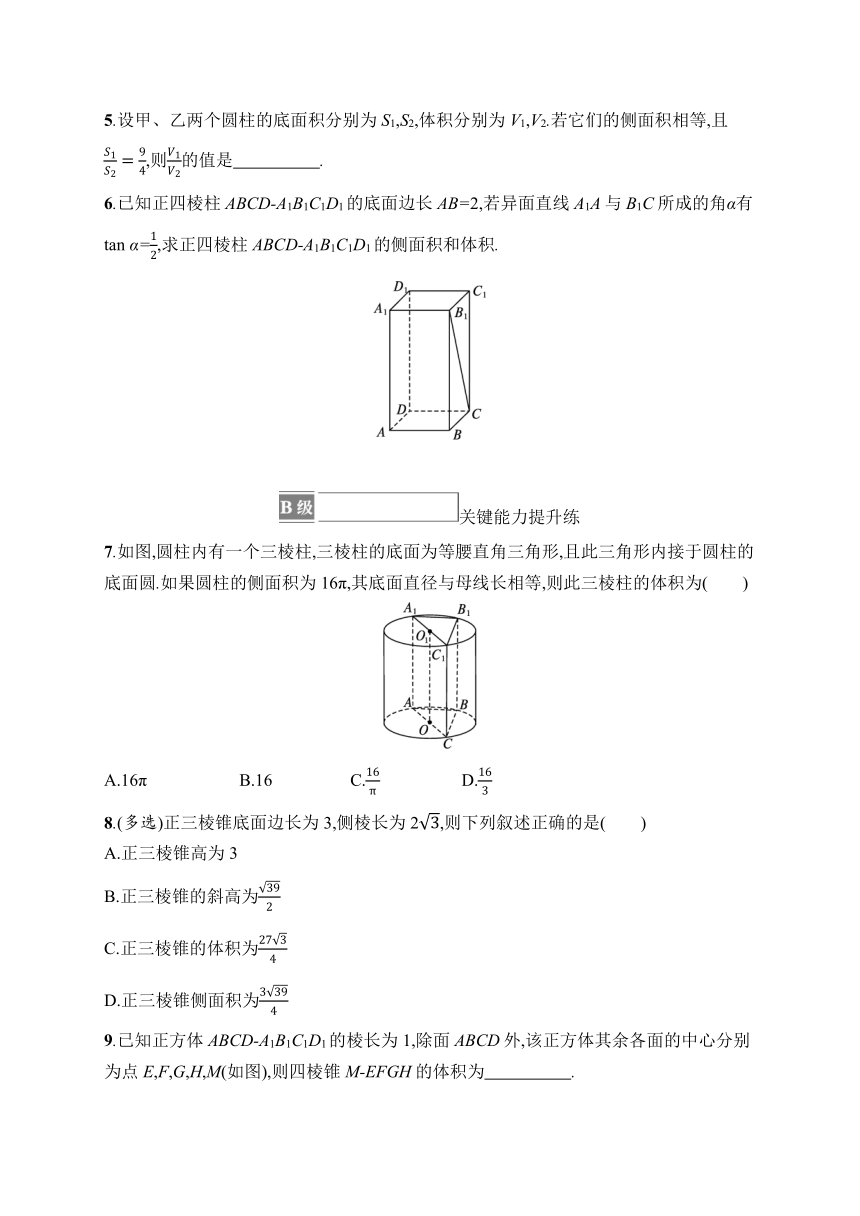
1.一个几何体的三视图如图所示,其中俯视图是圆的一部分,则该几何体的体积为( )
A. B. C.π D.2π
2.如图,在梯形ABCD中,∠ABC=90°,AD∥BC,BC=2AD=2AB=2,将梯形ABCD绕AD所在的直线旋转一周所围成的几何体的体积为( )
A.π B.π C.π D.2π
3.华裔建筑师贝聿铭设计的巴黎卢浮宫金字塔的形状可视为一个正四棱锥(底面是正方形,侧棱长都相等的四棱锥),四个侧面由673块玻璃拼组而成,塔高21 m,底宽34 m,则该金字塔的体积为( )
A.8 092 m3
B.4 046 m3
C.2 427 m3
D.12 138 m3
4.圆锥的侧面展开图为扇形,若其弧长为2π cm,半径为 cm,则该圆锥的底面圆半径为 cm;圆锥的体积为 cm3.
5.设甲、乙两个圆柱的底面积分别为S1,S2,体积分别为V1,V2.若它们的侧面积相等,且,则的值是 .
6.已知正四棱柱ABCD-A1B1C1D1的底面边长AB=2,若异面直线A1A与B1C所成的角α有tan α=,求正四棱柱ABCD-A1B1C1D1的侧面积和体积.
关键能力提升练
7.如图,圆柱内有一个三棱柱,三棱柱的底面为等腰直角三角形,且此三角形内接于圆柱的底面圆.如果圆柱的侧面积为16π,其底面直径与母线长相等,则此三棱柱的体积为( )
A.16π B.16 C. D.
8.(多选)正三棱锥底面边长为3,侧棱长为2,则下列叙述正确的是( )
A.正三棱锥高为3
B.正三棱锥的斜高为
C.正三棱锥的体积为
D.正三棱锥侧面积为
9.已知正方体ABCD-A1B1C1D1的棱长为1,除面ABCD外,该正方体其余各面的中心分别为点E,F,G,H,M(如图),则四棱锥M-EFGH的体积为 .
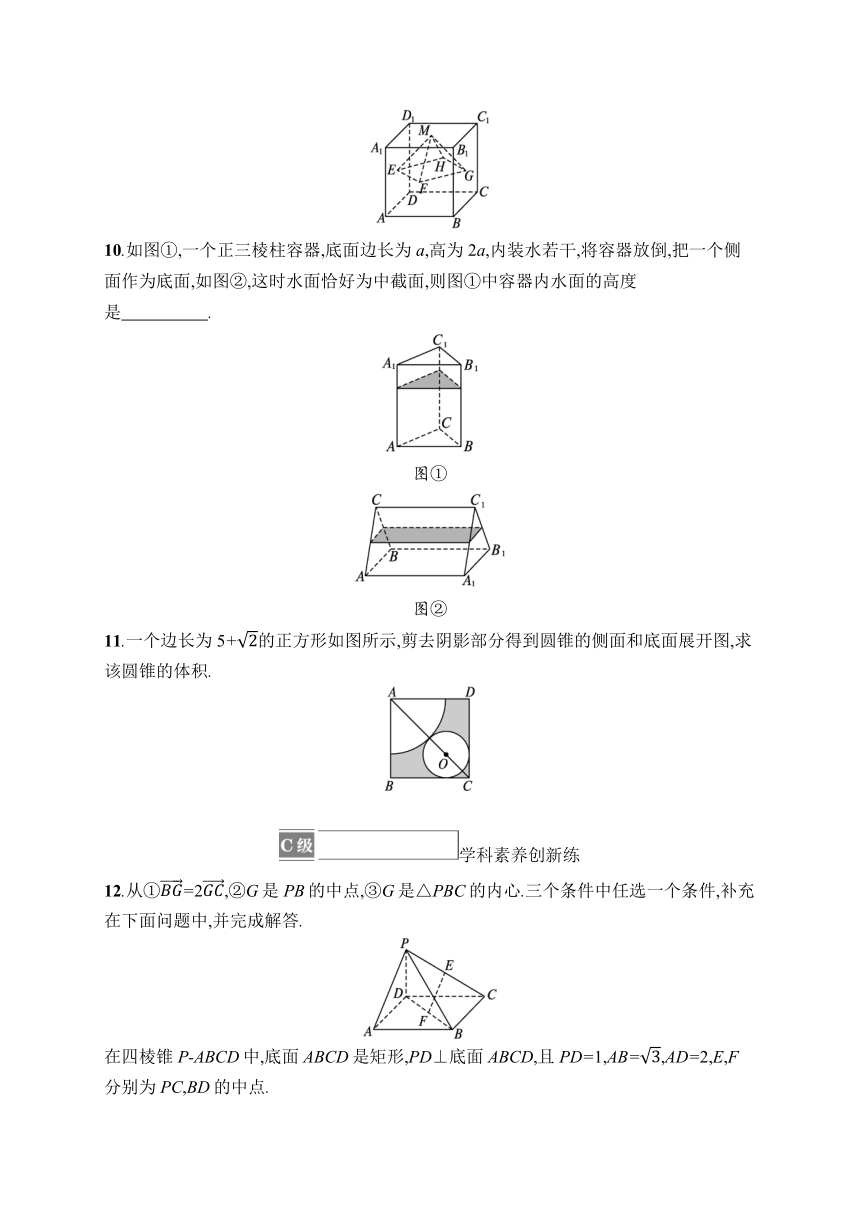
10.如图①,一个正三棱柱容器,底面边长为a,高为2a,内装水若干,将容器放倒,把一个侧面作为底面,如图②,这时水面恰好为中截面,则图①中容器内水面的高度是 .
图①
图②
11.一个边长为5+的正方形如图所示,剪去阴影部分得到圆锥的侧面和底面展开图,求该圆锥的体积.
学科素养创新练
12.从①=2,②G是PB的中点,③G是△PBC的内心.三个条件中任选一个条件,补充在下面问题中,并完成解答.
在四棱锥P-ABCD中,底面ABCD是矩形,PD⊥底面ABCD,且PD=1,AB=,AD=2,E,F分别为PC,BD的中点.
(1)判断EF与平面PAD的位置关系,并证明你的结论;
(2)若G是侧面PBC上的一点,且 ,求三棱锥G-DCE的体积.
(注:如果选择多个条件分别解答,则按第一个解答计分.)
答案
1.C 几何体为圆柱被轴截面切掉的图形,其体积等于圆柱体积的一半,圆柱的底面半径为1,高为2,所以该几何体的体积V=π×12×2=π.
2.A 由题意,旋转而成的几何体是圆柱,挖去一个圆锥,如图所示,
该几何体的体积为π×12×2-×π×12×1=π.
故选A.
3.A 如图,
正四棱锥P-ABCD中,PO⊥底面ABCD,PO=21 m,AB=34 m,底面正方形的面积为S=34×34=1 156 m2,则正四棱锥P-ABCD的体积为×S×PO=×1 156×21=8 092 m3.
故选A.
4.1 因为圆锥的侧面展开图的弧长为2π cm,半径为 cm,故圆锥的底面圆周长为2π cm,母线长为 cm,则圆锥的底面圆半径为1 cm,高为1 cm,则圆锥的体积V=×π×12×1= cm3.
5. 设两个圆柱的底面半径和高分别为r1,r2和h1,h2,由,得,则.由圆柱的侧面积相等,得2πr1h1=2πr2h2,即r1h1=r2h2,所以.
6.解因为AA1∥BB1,
所以直线A1A与B1C所成角是∠CB1B,
所以tan∠CB1B=.
因为BC=AB=2,所以BB1=4.
所以正四棱柱ABCD-A1B1C1D1的侧面积S=4×2×4=32,体积V=2×2×4=16.
7.B 设圆柱的底面半径为r,则该圆柱的母线长为2r,圆柱的侧面积为2πr×2r=4πr2=16π,解得r=2,
因为三棱柱ABC-A1B1C1的底面为等腰直角三角形,
由题图可知,AC为等腰直角三角形ABC的斜边,故O,O1分别为AC,A1C1的中点,
因为AA1∥CC1且AA1=CC1,故四边形AA1C1C为平行四边形,所以AC∥A1C1且AC=A1C1.
因为O,O1分别为AC,A1C1的中点,则AO∥A1O1且AO=A1O1,
所以四边形AA1O1O为平行四边形,所以AA1∥OO1且AA1=OO1=2r=4.
因为OO1⊥底面ABC,故AA1⊥底面ABC,所以三棱柱ABC-A1B1C1为直三棱柱,
易得AB=BC=AC=r=2,S△ABC=AB2=4,
因此,三棱柱ABC-A1B1C1的体积为=S△ABC·AA1=16.
8.AB 取△ABC的中心为O,连接PO.
由题意得PO⊥平面ABC.
因为△ABC为等边三角形,所以AO=,
所以正三棱锥的高为PO==3,
所以S△ABC=×3×3sin 60°=,所以正三棱锥的体积为VP-ABC=S△ABCPO=.
作PD⊥AB交AB于D,因为PA=PB=2,AD=AB=,所以正三棱锥的斜高为PD=,所以正三棱锥的侧面积为3S△PAB=3××PD×AB=3××3=.故选AB.
9. 连接AD1,CD1,B1A,B1C,AC(图略).
∵E,H分别为AD1,CD1的中点,∴EH∥AC,EH=AC.
∵F,G分别为B1A,B1C的中点,∴FG∥AC,FG=AC,
∴EH∥FG,EH=FG,∴四边形EFGH为平行四边形.
又EG=HF,EH=HG,∴四边形EFGH为正方形.
又四棱锥M-EFGH的高为,EF=,
∴四棱锥M-EFGH的体积为×2×.
10.a 设题图①中容器内水面的高度为h,水的体积为V,则V=S△ABCh.
又题图②中水组成了一个直四棱柱,其底面积为S△ABC,高度为2a,则V=S△ABC·2a,
所以h=a.
11.解设圆锥的底面半径为r,母线长为l,高为h,则依题意有·2πl=2πr,所以l=4r.
又因为AC=OC+OA=r+r+l=(+5)r,
且AC=×(+5),
所以(+5)r=(+5)×,
所以r=,所以l=4,
所以h=,
所以V圆锥=πr2h=π×()2×π.
故该圆锥的体积为π.
12.解(1)EF∥平面PAD,
理由如下:
如图所示,连接AC.
∵四边形ABCD为矩形,且点F为BD的中点,
∴点F为AC的中点.
又E为PC的中点,
∴EF∥PA.
∵EF 平面PAD,PA 平面PAD,
∴EF∥平面PAD.
(2)∵四边形ABCD为矩形,
∴BC⊥CD.
∵PD⊥平面ABCD,BC 平面ABCD,
∴BC⊥PD.
∵CD∩PD=D,
∴BC⊥平面PCD.
∵E为PC的中点,则S△DEC=S△PCD=CD×PD=×1=.
选①:=2,则G∈BC,
∴GC⊥平面PCD,
且GC=BC=,
∴VG-DEC=S△DEC×GC=.
选②:∵G,E分别为PB,PC的中点,
∴GE∥BC,且GE=BC=1.
∵BC⊥平面PCD,
∴GE⊥平面PCD,
∴VG-DEC=S△DEC×GE=×1=.
选③:设△PBC的内切圆切PC于点H,连接GH,则GH⊥PC.
∵BC⊥平面PCD,PC 平面PCD,
∴BC⊥PC.
在平面PBC内,BC⊥PC,GH⊥PC,则GH∥BC,
∴GH⊥平面PCD,PC==2,PB==2.
由等面积法可得S△PBC=BC×PC=(PC+BC+PB)×GH,
∴GH==2-,
必备知识基础练
1.一个几何体的三视图如图所示,其中俯视图是圆的一部分,则该几何体的体积为( )
A. B. C.π D.2π
2.如图,在梯形ABCD中,∠ABC=90°,AD∥BC,BC=2AD=2AB=2,将梯形ABCD绕AD所在的直线旋转一周所围成的几何体的体积为( )
A.π B.π C.π D.2π
3.华裔建筑师贝聿铭设计的巴黎卢浮宫金字塔的形状可视为一个正四棱锥(底面是正方形,侧棱长都相等的四棱锥),四个侧面由673块玻璃拼组而成,塔高21 m,底宽34 m,则该金字塔的体积为( )
A.8 092 m3
B.4 046 m3
C.2 427 m3
D.12 138 m3
4.圆锥的侧面展开图为扇形,若其弧长为2π cm,半径为 cm,则该圆锥的底面圆半径为 cm;圆锥的体积为 cm3.
5.设甲、乙两个圆柱的底面积分别为S1,S2,体积分别为V1,V2.若它们的侧面积相等,且,则的值是 .
6.已知正四棱柱ABCD-A1B1C1D1的底面边长AB=2,若异面直线A1A与B1C所成的角α有tan α=,求正四棱柱ABCD-A1B1C1D1的侧面积和体积.
关键能力提升练
7.如图,圆柱内有一个三棱柱,三棱柱的底面为等腰直角三角形,且此三角形内接于圆柱的底面圆.如果圆柱的侧面积为16π,其底面直径与母线长相等,则此三棱柱的体积为( )
A.16π B.16 C. D.
8.(多选)正三棱锥底面边长为3,侧棱长为2,则下列叙述正确的是( )
A.正三棱锥高为3
B.正三棱锥的斜高为
C.正三棱锥的体积为
D.正三棱锥侧面积为
9.已知正方体ABCD-A1B1C1D1的棱长为1,除面ABCD外,该正方体其余各面的中心分别为点E,F,G,H,M(如图),则四棱锥M-EFGH的体积为 .
10.如图①,一个正三棱柱容器,底面边长为a,高为2a,内装水若干,将容器放倒,把一个侧面作为底面,如图②,这时水面恰好为中截面,则图①中容器内水面的高度是 .
图①
图②
11.一个边长为5+的正方形如图所示,剪去阴影部分得到圆锥的侧面和底面展开图,求该圆锥的体积.
学科素养创新练
12.从①=2,②G是PB的中点,③G是△PBC的内心.三个条件中任选一个条件,补充在下面问题中,并完成解答.
在四棱锥P-ABCD中,底面ABCD是矩形,PD⊥底面ABCD,且PD=1,AB=,AD=2,E,F分别为PC,BD的中点.
(1)判断EF与平面PAD的位置关系,并证明你的结论;
(2)若G是侧面PBC上的一点,且 ,求三棱锥G-DCE的体积.
(注:如果选择多个条件分别解答,则按第一个解答计分.)
答案
1.C 几何体为圆柱被轴截面切掉的图形,其体积等于圆柱体积的一半,圆柱的底面半径为1,高为2,所以该几何体的体积V=π×12×2=π.
2.A 由题意,旋转而成的几何体是圆柱,挖去一个圆锥,如图所示,
该几何体的体积为π×12×2-×π×12×1=π.
故选A.
3.A 如图,
正四棱锥P-ABCD中,PO⊥底面ABCD,PO=21 m,AB=34 m,底面正方形的面积为S=34×34=1 156 m2,则正四棱锥P-ABCD的体积为×S×PO=×1 156×21=8 092 m3.
故选A.
4.1 因为圆锥的侧面展开图的弧长为2π cm,半径为 cm,故圆锥的底面圆周长为2π cm,母线长为 cm,则圆锥的底面圆半径为1 cm,高为1 cm,则圆锥的体积V=×π×12×1= cm3.
5. 设两个圆柱的底面半径和高分别为r1,r2和h1,h2,由,得,则.由圆柱的侧面积相等,得2πr1h1=2πr2h2,即r1h1=r2h2,所以.
6.解因为AA1∥BB1,
所以直线A1A与B1C所成角是∠CB1B,
所以tan∠CB1B=.
因为BC=AB=2,所以BB1=4.
所以正四棱柱ABCD-A1B1C1D1的侧面积S=4×2×4=32,体积V=2×2×4=16.
7.B 设圆柱的底面半径为r,则该圆柱的母线长为2r,圆柱的侧面积为2πr×2r=4πr2=16π,解得r=2,
因为三棱柱ABC-A1B1C1的底面为等腰直角三角形,
由题图可知,AC为等腰直角三角形ABC的斜边,故O,O1分别为AC,A1C1的中点,
因为AA1∥CC1且AA1=CC1,故四边形AA1C1C为平行四边形,所以AC∥A1C1且AC=A1C1.
因为O,O1分别为AC,A1C1的中点,则AO∥A1O1且AO=A1O1,
所以四边形AA1O1O为平行四边形,所以AA1∥OO1且AA1=OO1=2r=4.
因为OO1⊥底面ABC,故AA1⊥底面ABC,所以三棱柱ABC-A1B1C1为直三棱柱,
易得AB=BC=AC=r=2,S△ABC=AB2=4,
因此,三棱柱ABC-A1B1C1的体积为=S△ABC·AA1=16.
8.AB 取△ABC的中心为O,连接PO.
由题意得PO⊥平面ABC.
因为△ABC为等边三角形,所以AO=,
所以正三棱锥的高为PO==3,
所以S△ABC=×3×3sin 60°=,所以正三棱锥的体积为VP-ABC=S△ABCPO=.
作PD⊥AB交AB于D,因为PA=PB=2,AD=AB=,所以正三棱锥的斜高为PD=,所以正三棱锥的侧面积为3S△PAB=3××PD×AB=3××3=.故选AB.
9. 连接AD1,CD1,B1A,B1C,AC(图略).
∵E,H分别为AD1,CD1的中点,∴EH∥AC,EH=AC.
∵F,G分别为B1A,B1C的中点,∴FG∥AC,FG=AC,
∴EH∥FG,EH=FG,∴四边形EFGH为平行四边形.
又EG=HF,EH=HG,∴四边形EFGH为正方形.
又四棱锥M-EFGH的高为,EF=,
∴四棱锥M-EFGH的体积为×2×.
10.a 设题图①中容器内水面的高度为h,水的体积为V,则V=S△ABCh.
又题图②中水组成了一个直四棱柱,其底面积为S△ABC,高度为2a,则V=S△ABC·2a,
所以h=a.
11.解设圆锥的底面半径为r,母线长为l,高为h,则依题意有·2πl=2πr,所以l=4r.
又因为AC=OC+OA=r+r+l=(+5)r,
且AC=×(+5),
所以(+5)r=(+5)×,
所以r=,所以l=4,
所以h=,
所以V圆锥=πr2h=π×()2×π.
故该圆锥的体积为π.
12.解(1)EF∥平面PAD,
理由如下:
如图所示,连接AC.
∵四边形ABCD为矩形,且点F为BD的中点,
∴点F为AC的中点.
又E为PC的中点,
∴EF∥PA.
∵EF 平面PAD,PA 平面PAD,
∴EF∥平面PAD.
(2)∵四边形ABCD为矩形,
∴BC⊥CD.
∵PD⊥平面ABCD,BC 平面ABCD,
∴BC⊥PD.
∵CD∩PD=D,
∴BC⊥平面PCD.
∵E为PC的中点,则S△DEC=S△PCD=CD×PD=×1=.
选①:=2,则G∈BC,
∴GC⊥平面PCD,
且GC=BC=,
∴VG-DEC=S△DEC×GC=.
选②:∵G,E分别为PB,PC的中点,
∴GE∥BC,且GE=BC=1.
∵BC⊥平面PCD,
∴GE⊥平面PCD,
∴VG-DEC=S△DEC×GE=×1=.
选③:设△PBC的内切圆切PC于点H,连接GH,则GH⊥PC.
∵BC⊥平面PCD,PC 平面PCD,
∴BC⊥PC.
在平面PBC内,BC⊥PC,GH⊥PC,则GH∥BC,
∴GH⊥平面PCD,PC==2,PB==2.
由等面积法可得S△PBC=BC×PC=(PC+BC+PB)×GH,
∴GH==2-,
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
