高中数学北师大版(2019)必修第二册同步试题:第6章 6-3 球的表面积和体积(含解析)
文档属性
| 名称 | 高中数学北师大版(2019)必修第二册同步试题:第6章 6-3 球的表面积和体积(含解析) |
|
|
| 格式 | zip | ||
| 文件大小 | 251.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-22 00:00:00 | ||
图片预览

文档简介
6.3 球的表面积和体积
必备知识基础练
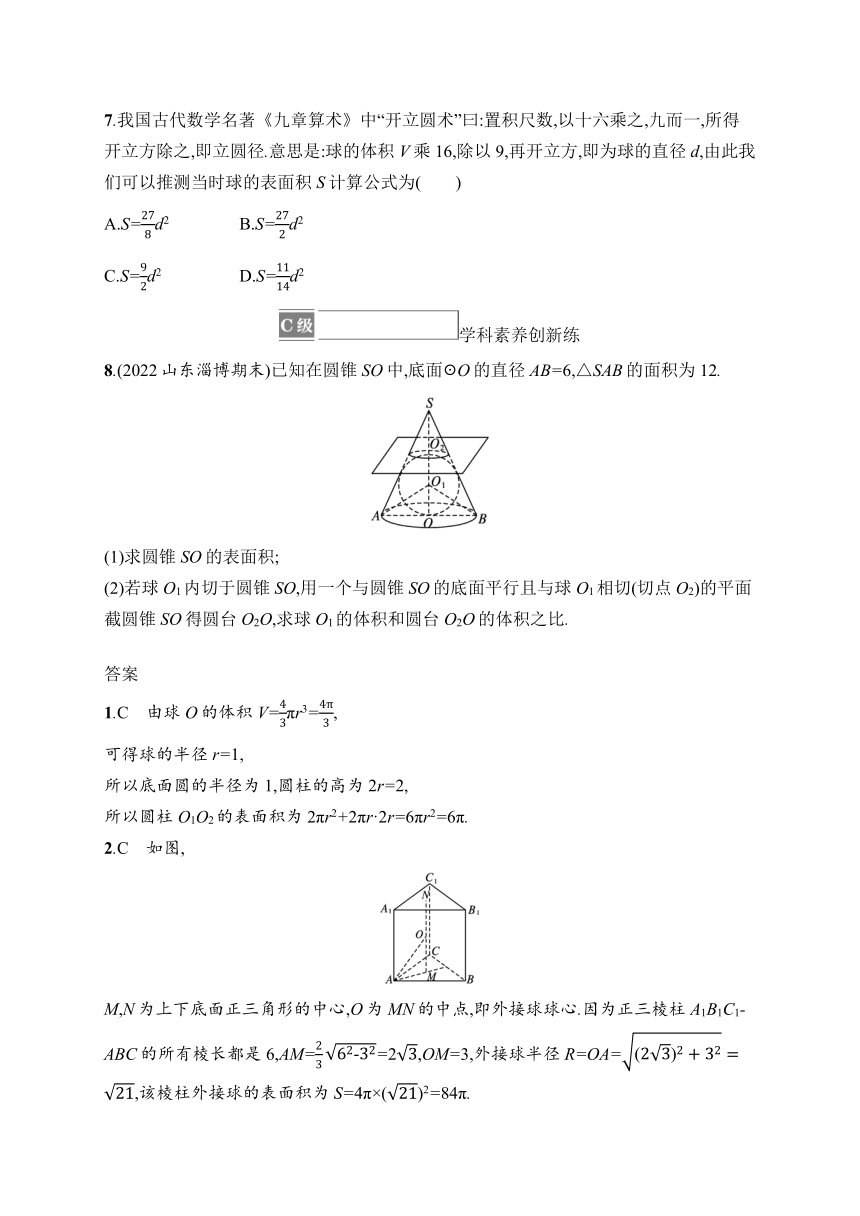
1.如图,该球O与圆柱O1O2的上、下底面及母线均相切,若球O的体积为,则圆柱O1O2的表面积为( )
A.4π B.5π
C.6π D.7π
2.已知正三棱柱A1B1C1-ABC的所有棱长都是6,则该棱柱外接球的表面积为( )
A.21π B.42π C.84π D.84
3.若长方体的长、宽、高分别为3,2,1,其顶点都在球O的球面上,则球O的表面积为 .
4.已知三个球的半径分别为R1,R2,R3,且满足R1+2R2=3R3,则它们相应的表面积S1,S2,S3满足的等量关系是 ,它们相应的体积V1,V2,V3满足的等量关系是 .
关键能力提升练
5.一个正四棱柱的各个顶点都在一个半径为2 cm的球面上,如果正四棱柱的底面边长为2 cm,那么该棱柱的表面积为( )
A.2+4 cm2 B.8+16 cm2
C.4+8 cm2 D.16+32 cm2
6.已知一个几何体的三视图如图,则其外接球的体积为( )
A.18π B.27π C.36π D.45π
7.我国古代数学名著《九章算术》中“开立圆术”曰:置积尺数,以十六乘之,九而一,所得开立方除之,即立圆径.意思是:球的体积V乘16,除以9,再开立方,即为球的直径d,由此我们可以推测当时球的表面积S计算公式为( )
A.S=d2 B.S=d2
C.S=d2 D.S=d2
学科素养创新练
8.(2022山东淄博期末)已知在圆锥SO中,底面☉O的直径AB=6,△SAB的面积为12.
(1)求圆锥SO的表面积;
(2)若球O1内切于圆锥SO,用一个与圆锥SO的底面平行且与球O1相切(切点O2)的平面截圆锥SO得圆台O2O,求球O1的体积和圆台O2O的体积之比.
答案
1.C 由球O的体积V=πr3=,
可得球的半径r=1,
所以底面圆的半径为1,圆柱的高为2r=2,
所以圆柱O1O2的表面积为2πr2+2πr·2r=6πr2=6π.
2.C 如图,
M,N为上下底面正三角形的中心,O为MN的中点,即外接球球心.因为正三棱柱A1B1C1-ABC的所有棱长都是6,AM==2,OM=3,外接球半径R=OA=,该棱柱外接球的表面积为S=4π×()2=84π.
3.14π 球的直径是长方体的体对角线,所以2R=,
所以球O的表面积为S=4πR2=14π.
4.+2=3+2=3 因为S1=4π,所以R1=,同理可得R2=,R3=.由R1+2R2=3R3,得+2=3.
由V1=,得R1=.
同理可得R2=,R3=.
由R1+2R2=3R3,得+2=3.
5.B 设正四棱柱的高为h,则由题意及球的性质可得,=2R=4,所以h=2(cm),所以该棱柱的表面积为2×22+4×2×2=8+16(cm2),故选B.
6.C 根据三视图还原原几何体,如图所示:
由图可知,该几何体为三棱锥A-BCD,且AB⊥平面BCD,
将三棱锥A-BCD补成长方体AEFG-BCDH,
所以,三棱锥A-BCD的外接球直径为2R==6,故R=3,
因此,该几何体的外接球的体积为V=πR3=36π.
7.A 因为=d,所以V=3,
所以π=,所以S=4π2=4×d2.
故选A.
8.解(1)设圆锥SO的母线长为l,底面☉O的直径为2r,
所以2r=6.
因为△SAB的面积为12,
所以S△SAB=·2r×SO=12,
解得SO=4.
由勾股定理得l==5,
由圆锥的表面积公式得S表=S侧+S底=πrl+πr2=15π+9π=24π.
(2)作圆锥的轴截面,如图.
因为球O1内切于圆锥SO,
所以O1H⊥SB,
所以△SO1H∽△SBO,
设球O1的半径为r',
则,
即,解得r'=,
所以球O1的体积为πr'3=,
由题知,△SO2D∽△SOB,
所以,
即,
解得O2D=,
所以圆O2的面积S'=π2=π.
又圆O的面积S=π×32=9π,圆台的高记为h,
所以h=2r'=3.
由圆台的体积公式有(S+S'+)h=9π+π+·3=π,
必备知识基础练
1.如图,该球O与圆柱O1O2的上、下底面及母线均相切,若球O的体积为,则圆柱O1O2的表面积为( )
A.4π B.5π
C.6π D.7π
2.已知正三棱柱A1B1C1-ABC的所有棱长都是6,则该棱柱外接球的表面积为( )
A.21π B.42π C.84π D.84
3.若长方体的长、宽、高分别为3,2,1,其顶点都在球O的球面上,则球O的表面积为 .
4.已知三个球的半径分别为R1,R2,R3,且满足R1+2R2=3R3,则它们相应的表面积S1,S2,S3满足的等量关系是 ,它们相应的体积V1,V2,V3满足的等量关系是 .
关键能力提升练
5.一个正四棱柱的各个顶点都在一个半径为2 cm的球面上,如果正四棱柱的底面边长为2 cm,那么该棱柱的表面积为( )
A.2+4 cm2 B.8+16 cm2
C.4+8 cm2 D.16+32 cm2
6.已知一个几何体的三视图如图,则其外接球的体积为( )
A.18π B.27π C.36π D.45π
7.我国古代数学名著《九章算术》中“开立圆术”曰:置积尺数,以十六乘之,九而一,所得开立方除之,即立圆径.意思是:球的体积V乘16,除以9,再开立方,即为球的直径d,由此我们可以推测当时球的表面积S计算公式为( )
A.S=d2 B.S=d2
C.S=d2 D.S=d2
学科素养创新练
8.(2022山东淄博期末)已知在圆锥SO中,底面☉O的直径AB=6,△SAB的面积为12.
(1)求圆锥SO的表面积;
(2)若球O1内切于圆锥SO,用一个与圆锥SO的底面平行且与球O1相切(切点O2)的平面截圆锥SO得圆台O2O,求球O1的体积和圆台O2O的体积之比.
答案
1.C 由球O的体积V=πr3=,
可得球的半径r=1,
所以底面圆的半径为1,圆柱的高为2r=2,
所以圆柱O1O2的表面积为2πr2+2πr·2r=6πr2=6π.
2.C 如图,
M,N为上下底面正三角形的中心,O为MN的中点,即外接球球心.因为正三棱柱A1B1C1-ABC的所有棱长都是6,AM==2,OM=3,外接球半径R=OA=,该棱柱外接球的表面积为S=4π×()2=84π.
3.14π 球的直径是长方体的体对角线,所以2R=,
所以球O的表面积为S=4πR2=14π.
4.+2=3+2=3 因为S1=4π,所以R1=,同理可得R2=,R3=.由R1+2R2=3R3,得+2=3.
由V1=,得R1=.
同理可得R2=,R3=.
由R1+2R2=3R3,得+2=3.
5.B 设正四棱柱的高为h,则由题意及球的性质可得,=2R=4,所以h=2(cm),所以该棱柱的表面积为2×22+4×2×2=8+16(cm2),故选B.
6.C 根据三视图还原原几何体,如图所示:
由图可知,该几何体为三棱锥A-BCD,且AB⊥平面BCD,
将三棱锥A-BCD补成长方体AEFG-BCDH,
所以,三棱锥A-BCD的外接球直径为2R==6,故R=3,
因此,该几何体的外接球的体积为V=πR3=36π.
7.A 因为=d,所以V=3,
所以π=,所以S=4π2=4×d2.
故选A.
8.解(1)设圆锥SO的母线长为l,底面☉O的直径为2r,
所以2r=6.
因为△SAB的面积为12,
所以S△SAB=·2r×SO=12,
解得SO=4.
由勾股定理得l==5,
由圆锥的表面积公式得S表=S侧+S底=πrl+πr2=15π+9π=24π.
(2)作圆锥的轴截面,如图.
因为球O1内切于圆锥SO,
所以O1H⊥SB,
所以△SO1H∽△SBO,
设球O1的半径为r',
则,
即,解得r'=,
所以球O1的体积为πr'3=,
由题知,△SO2D∽△SOB,
所以,
即,
解得O2D=,
所以圆O2的面积S'=π2=π.
又圆O的面积S=π×32=9π,圆台的高记为h,
所以h=2r'=3.
由圆台的体积公式有(S+S'+)h=9π+π+·3=π,
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
