人教版六年级下册数学 圆柱与圆锥的复习课课件(共19张PPT)
文档属性
| 名称 | 人教版六年级下册数学 圆柱与圆锥的复习课课件(共19张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 370.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-07 11:37:17 | ||
图片预览




文档简介
(共19张PPT)
圆柱与圆锥复习课
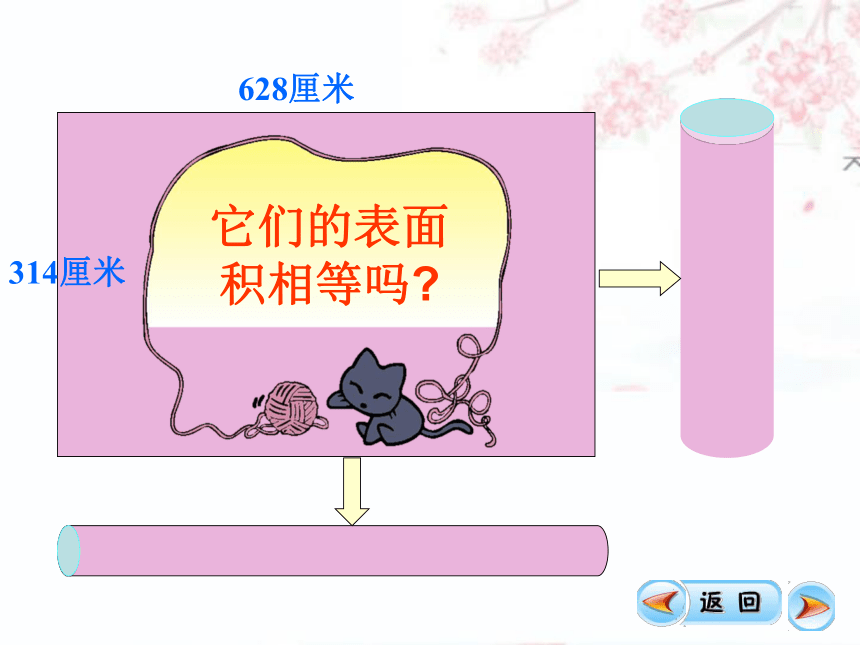
628厘米
314厘米
它们的表面积相等吗
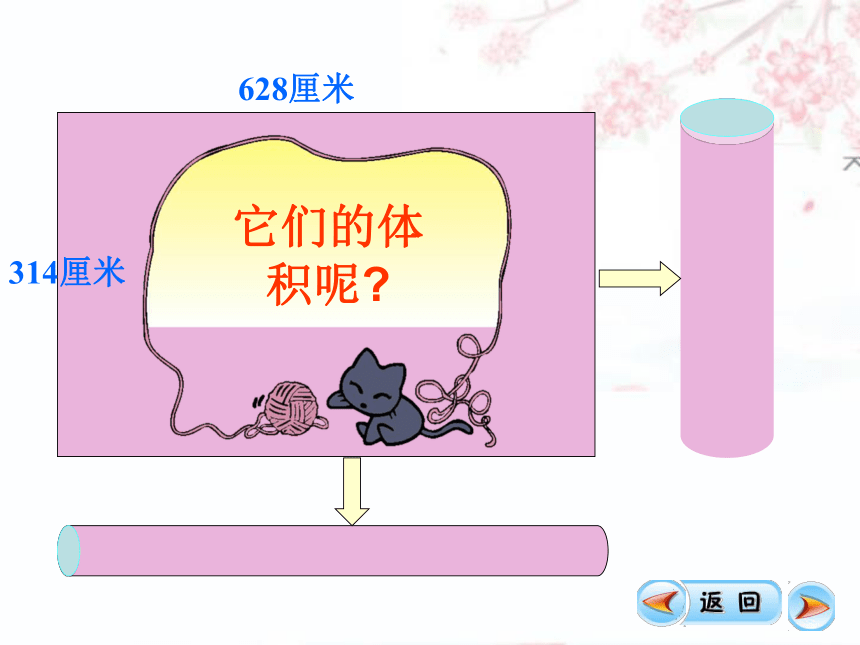
628厘米
314厘米
它们的体积呢
把下面的圆柱形木料,截成两段,它的表面积会有怎样的变化?
13、把3个完全相同的圆柱叠放在一起(底面半径5厘米)。拿走一个圆柱,表面积就减少628平方厘米。每个圆柱的体积是多少立方厘米?
思维拓展:
动脑筋
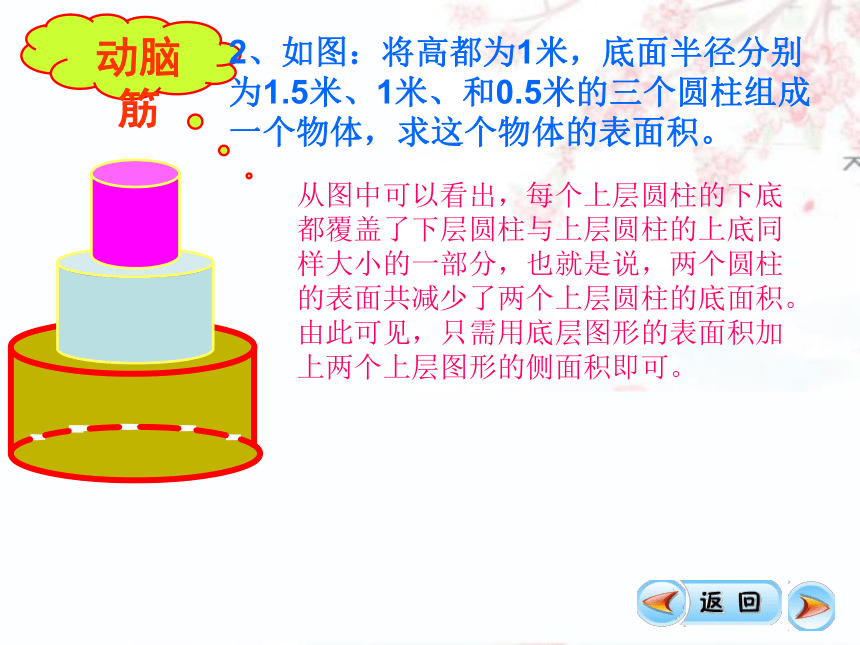
2、如图:将高都为1米,底面半径分别为1.5米、1米、和0.5米的三个圆柱组成一个物体,求这个物体的表面积。
从图中可以看出,每个上层圆柱的下底都覆盖了下层圆柱与上层圆柱的上底同样大小的一部分,也就是说,两个圆柱的表面共减少了两个上层圆柱的底面积。由此可见,只需用底层图形的表面积加上两个上层图形的侧面积即可。
有一根圆柱形的木材,底面直径是16厘米,高是20厘米沿着它的底面直径, 从上向下锯成相等的两块(如图),每块的表面积是多少
动脑筋
挑战自我
把一个高10厘米的圆柱,按下图切开,拼成一个近似的长方体。表面积就增加了( )平方厘米.
60
10cm
10cm
5cm
把一根长和宽都是10厘米、高是5厘米的长方体木料加工成一个最大的圆柱体木块。求这个圆柱体木块的体积。
10
2
3.14( )2×5
=392.5(立方厘米)
答:这个圆柱体木块的体积是392.5立方厘米。
50cm
40cm
30cm
把一个长50厘米,宽40厘米、高30厘米的长方体木料加工成一个最大的圆柱体木块。求这个圆柱体木块的体积。
5、将一个圆柱体沿着底面直径切成两个半圆柱,表面积增加了40平方厘米,圆柱的底面直径为4厘米,这个圆柱的体积是多少立方厘米
思维拓展:
一个长方形的长是8厘米,宽是5厘米,分别以长和宽为轴旋转(如图),形成了两个圆柱,比较这两个圆柱的表面积和体积,哪一个大?大多少?
1、长方形怎样做成一个圆柱?
思维拓展:
3、如图,想想办法,你能否求它的体积 ( 单位:厘米)
2
6
4
思维拓展:
计算下面钢管的表面积。(单位:厘米)
6
8
100
空心圆柱体的表面积
钢管的表面积等于大圆柱的侧面积加上小圆柱的侧面积,再加上两个圆环的面积。
将石块放入半径为10厘米的乙容器,水位上升2厘米,再将石块放入半径为20厘米的甲容器,水位应上升多少厘米?
4、一个酒瓶里面深30厘米,底面直径是8厘米,瓶里有酒深10厘米,把酒瓶塞紧后倒置(瓶口向下),这时酒深20厘米,你能算出酒瓶的容积是多少毫升来吗
10
20
30
8
思维拓展:
求侧面积的一半+1个底面积
求圆柱体积的一半
6、一个用塑料薄膜覆盖的疏菜大棚,长15米,横截面是一个半径2米的半圆。
(1)覆盖在这个大棚上的塑料薄膜约有多少平方米?
(2)大棚内的空间大约有多大?
思维拓展:
1、一个圆柱形玻璃容器底面直径是10厘米。把一块铁从这个容器的水中取出后,水面下降2厘米。这块铁的体积是多少?
2、在直径0.8米的水管中,水流速度是每秒2米,那么1分钟流过的水有多少立方米?
3、把一个棱长6分米的正方体木块切削成一个体积最大的圆柱体,这个圆柱的体积是多少立方分米?
4、一个长方体,底面是一个正方形,底边长是4分米,高是8分米,完全浸入到一个盛满水的圆柱形容器里,容器的底面积为32平方分米。水面会升高多少厘米?
5、一个圆柱体的高是 10厘米。如果高减少3厘米,则表面积比原来减少94.2平方厘米,原来圆柱体的体积是多少立方厘米?
6、一个圆柱的高是10厘米,如果高减少3厘米,则表面积减少94.2平方厘米,原来圆柱的体积是多少立方厘米?
7、把一个棱长是8厘米的正方体铁块熔铸成一个底面直径是10厘米的圆柱形铁块,这个圆柱形铁块的高大约是多少厘米?(得数保留整厘米)
8、把一个底面半径是1分米,高是6分米的圆柱形木块加工成一个最大的圆锥。圆锥的体积是多少立方分米?要削去多少立方分米的木料?
9、一个圆锥形沙堆,底面积是25.12平方米,高是1.8米。用这堆沙在10米宽的公路上铺3厘米厚的路面,能铺多少米?
10、一个圆柱形水桶的容积为24立方分米,底面积是7.5平方分米,距桶口0.7分米处有一个漏洞,现在,这个水桶最多能装多少千克水?(每立方分米水的质量为1千克)
11、游乐场中心有一个长方体形的儿童游泳池,长24米,宽12.56米,深1.2米。如果用直径是24厘米的水管向游泳池里注水,水流速度按每分钟100米计算,注满这个游泳池要多少时间?
12、有一个圆柱,它的底面积和侧面积正好相等。如果这个圆柱的底面积不变,高增加3厘米,它的表面积就增加94.2平方厘米,求原来圆柱的表面积。
圆柱与圆锥复习课
628厘米
314厘米
它们的表面积相等吗
628厘米
314厘米
它们的体积呢
把下面的圆柱形木料,截成两段,它的表面积会有怎样的变化?
13、把3个完全相同的圆柱叠放在一起(底面半径5厘米)。拿走一个圆柱,表面积就减少628平方厘米。每个圆柱的体积是多少立方厘米?
思维拓展:
动脑筋
2、如图:将高都为1米,底面半径分别为1.5米、1米、和0.5米的三个圆柱组成一个物体,求这个物体的表面积。
从图中可以看出,每个上层圆柱的下底都覆盖了下层圆柱与上层圆柱的上底同样大小的一部分,也就是说,两个圆柱的表面共减少了两个上层圆柱的底面积。由此可见,只需用底层图形的表面积加上两个上层图形的侧面积即可。
有一根圆柱形的木材,底面直径是16厘米,高是20厘米沿着它的底面直径, 从上向下锯成相等的两块(如图),每块的表面积是多少
动脑筋
挑战自我
把一个高10厘米的圆柱,按下图切开,拼成一个近似的长方体。表面积就增加了( )平方厘米.
60
10cm
10cm
5cm
把一根长和宽都是10厘米、高是5厘米的长方体木料加工成一个最大的圆柱体木块。求这个圆柱体木块的体积。
10
2
3.14( )2×5
=392.5(立方厘米)
答:这个圆柱体木块的体积是392.5立方厘米。
50cm
40cm
30cm
把一个长50厘米,宽40厘米、高30厘米的长方体木料加工成一个最大的圆柱体木块。求这个圆柱体木块的体积。
5、将一个圆柱体沿着底面直径切成两个半圆柱,表面积增加了40平方厘米,圆柱的底面直径为4厘米,这个圆柱的体积是多少立方厘米
思维拓展:
一个长方形的长是8厘米,宽是5厘米,分别以长和宽为轴旋转(如图),形成了两个圆柱,比较这两个圆柱的表面积和体积,哪一个大?大多少?
1、长方形怎样做成一个圆柱?
思维拓展:
3、如图,想想办法,你能否求它的体积 ( 单位:厘米)
2
6
4
思维拓展:
计算下面钢管的表面积。(单位:厘米)
6
8
100
空心圆柱体的表面积
钢管的表面积等于大圆柱的侧面积加上小圆柱的侧面积,再加上两个圆环的面积。
将石块放入半径为10厘米的乙容器,水位上升2厘米,再将石块放入半径为20厘米的甲容器,水位应上升多少厘米?
4、一个酒瓶里面深30厘米,底面直径是8厘米,瓶里有酒深10厘米,把酒瓶塞紧后倒置(瓶口向下),这时酒深20厘米,你能算出酒瓶的容积是多少毫升来吗
10
20
30
8
思维拓展:
求侧面积的一半+1个底面积
求圆柱体积的一半
6、一个用塑料薄膜覆盖的疏菜大棚,长15米,横截面是一个半径2米的半圆。
(1)覆盖在这个大棚上的塑料薄膜约有多少平方米?
(2)大棚内的空间大约有多大?
思维拓展:
1、一个圆柱形玻璃容器底面直径是10厘米。把一块铁从这个容器的水中取出后,水面下降2厘米。这块铁的体积是多少?
2、在直径0.8米的水管中,水流速度是每秒2米,那么1分钟流过的水有多少立方米?
3、把一个棱长6分米的正方体木块切削成一个体积最大的圆柱体,这个圆柱的体积是多少立方分米?
4、一个长方体,底面是一个正方形,底边长是4分米,高是8分米,完全浸入到一个盛满水的圆柱形容器里,容器的底面积为32平方分米。水面会升高多少厘米?
5、一个圆柱体的高是 10厘米。如果高减少3厘米,则表面积比原来减少94.2平方厘米,原来圆柱体的体积是多少立方厘米?
6、一个圆柱的高是10厘米,如果高减少3厘米,则表面积减少94.2平方厘米,原来圆柱的体积是多少立方厘米?
7、把一个棱长是8厘米的正方体铁块熔铸成一个底面直径是10厘米的圆柱形铁块,这个圆柱形铁块的高大约是多少厘米?(得数保留整厘米)
8、把一个底面半径是1分米,高是6分米的圆柱形木块加工成一个最大的圆锥。圆锥的体积是多少立方分米?要削去多少立方分米的木料?
9、一个圆锥形沙堆,底面积是25.12平方米,高是1.8米。用这堆沙在10米宽的公路上铺3厘米厚的路面,能铺多少米?
10、一个圆柱形水桶的容积为24立方分米,底面积是7.5平方分米,距桶口0.7分米处有一个漏洞,现在,这个水桶最多能装多少千克水?(每立方分米水的质量为1千克)
11、游乐场中心有一个长方体形的儿童游泳池,长24米,宽12.56米,深1.2米。如果用直径是24厘米的水管向游泳池里注水,水流速度按每分钟100米计算,注满这个游泳池要多少时间?
12、有一个圆柱,它的底面积和侧面积正好相等。如果这个圆柱的底面积不变,高增加3厘米,它的表面积就增加94.2平方厘米,求原来圆柱的表面积。
