6.3.2二项式系数的性质-2022-2023学年高二数学同步精讲 课件(共26张PPT)
文档属性
| 名称 | 6.3.2二项式系数的性质-2022-2023学年高二数学同步精讲 课件(共26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-07 12:07:29 | ||
图片预览






文档简介
(共26张PPT)
直线
6.3.2 二项式系数的性质
问题导入
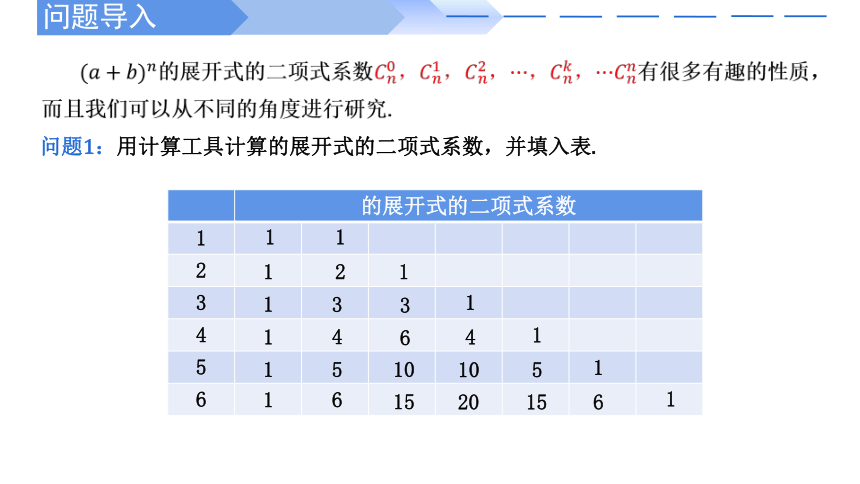
的展开式的二项式系数有很多有趣的性质,而且我们可以从不同的角度进行研究.
的展开式的二项式系数
1
2
3
4
5
6
问题1:用计算工具计算的展开式的二项式系数,并填入表.
1
1
1
1
2
1
1
3
3
1
1
4
4
6
1
1
5
5
10
10
1
1
6
6
15
15
20
新知探索
从上表中可以发现,每一行中的系数具有对称性.除此之外还有什么规律呢?为了便于发现规律,上表还可以写出如图所示的形式.
观察上图,你还能发现哪些规律?
新知探索
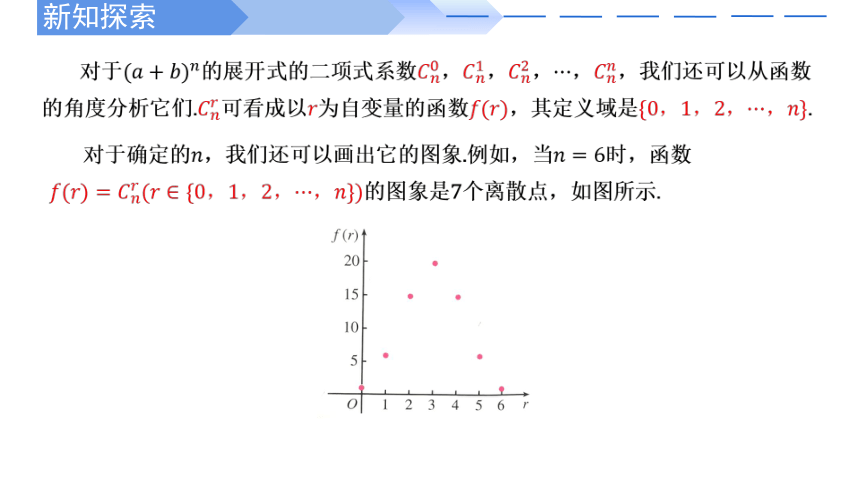
对于的展开式的二项式系数,,,,,我们还可以从函数的角度分析它们.可看成以为自变量的函数,其定义域是.
对于确定的,我们还可以画出它的图象.例如,当时,函数
的图象是7个离散点,如图所示.
新知探索
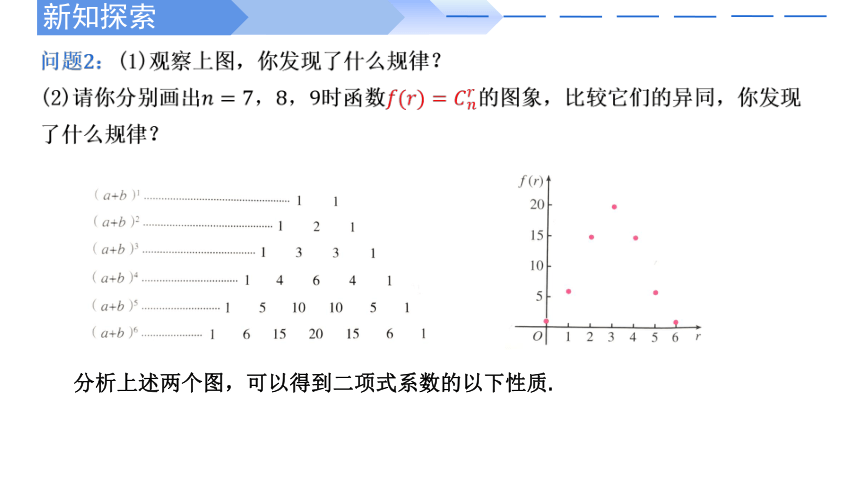
问题2:(1)观察上图,你发现了什么规律?
(2)请你分别画出时函数的图象,比较它们的异同,你发现了什么规律?
分析上述两个图,可以得到二项式系数的以下性质.
新知探索
1.对称性
与首末两端“等距离”的两个二项式系数相等.事实上,这一性质可直接由
得到.
直线将函数的图象分成对称的两部分,它是图象的对称轴.
2.增减性与最大值
因为,即,
所以,当,即时,随的增加而增大;由对称性知,当
时,随的增加而减小.当是偶数时,中间的一项取得最大值;当是奇数时,中间的两项与相等,且同时取得最大值.
新知探索
3.含二项式系数的和
已知,
令,得.
这就是说,的展开式的各二项式系数的和等于.
新知探索
答案:D.
辨析1.已知的展开式中只有第5项的二项式系数最大,则等于( ).
A.11 B.10 C.9 D.8
辨析2.的展开式中二项展系数最大的项是第_____项.
答案:4或5.
例析
例3.求证:在的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
l
解:在展开式 中,
令,,则得 .
即.
因此,,
即在的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
练习
题型一:求二项展开式中系数或二项式系数的最大项
例1.(1)的展开式中第6项与第7项的系数相等,则展开式中二项式系数最大的项为( ).
A.第5项 B.第6项或第7项 C.第6项 D.第7项
解:(1),,依题意有.
所以的展开式中,二项式系数最大的项为第5项.故选A.
答案:A.
练习
例1.(2)的展开式中,系数最大的项为( ).
A.第6项 B.第3项 C.第3项或第6项 D.第5项或第7项
解:(2)展开式中,二项式系数与对应的项的系数的绝对值相等.由于二项式系数的最大项为,且中的二项式系数的相反数,此时的系数最小.而,,且.所以系数最大的项为第5项和第7项.故选D.
答案:D.
练习
方法技巧:
(1)根据二项式系数的性质,为奇数时,中间两项的二项式系数最大;为偶数时,中间一项的二项式系数最大.
(2)求展开式中系数最大项与二项式系数最大项是不同的,需根据各项系数的正、负变化情况,一般采用列不等式(组),解不等式(组)的方法求解.一般地,如果第项的系数最大,则与之相邻两项(第项、第项)的系数均不大于第项的系数,由此列不等式组可确定的范围,再根据来确定的值,即可求出最大项.
练习
变1.(1)的展开式中系数最小的项为( ).
A.第6项 B.第7项 C.第8项 D.第9项
解(1):展开式中共有14项,中间两项(第7、8项)的二项式系数最大.由于二项展开式中二项式系数和项的系数满足:奇数项相等,偶数项互为相反数.所以系数最小的项为第8项,系数最大的项为第7项.故选C.
答案:C.
练习
变1.(2)在的展开式中,的系数等于-5,则该展开式的各项的系数中最大值为( ).
A.5 B.10 C.15 D.20
解(2):的展开式的通项,
令,则,所以,即,展开式中第2,4,6项的系数为负数,第1,3,5项的系数为正数,故各项的系数中最大值为.
答案:B.
练习
题型二:求二项展开式的系数和
例2.设
(1)求的值;
(2)求的值;
解:(1)令,得①
(2)令,得②
①②得,
∴.
练习
例2.设
(3)求的值.
解:(3)∵,
∴,.
∴.
练习
方法技巧:
二项展开式中系数和的求法
(1)对形如,的式子求其展开式的各项系数之和,常用赋值法,只需令即可;对的式子求其展开式各项系数之和,只需令即可.
(2)一般地,若,则展开式中各项系数之和为,奇数项系数之和为,偶数项系数之和为.
练习
变2.已知求:
(1);(2)
解:(1)由∵
令,得,
∴.
(2)由(1)得,,①
令得②
所以
练习
题型三:二项式系数性质的应用
例3.已知二项式
(1)若展开式中第5项,第6项,第7项的二项式系数成等差数列,求展开式中二项式系数最大项的系数;
解:(1)由题意,得,∴∴或
①当时,展开式中二项式系数最大的项是和,的系数为,的系数为.
故展开式中二项式系数最大项的系数分别为,.
②当时,展开式中二项式系数最大的项是,
∴的系数为.
故展开式中二项式系数最大项的系数分别为.
练习
例3.已知二项式
(2)若展开式中前三项的二项式系数和等于79,求展开式中系数最大的项.
解:(2)由题意知
解得或(舍去).
设展开式中第项的系数最大,由于,
则解得.
又,∴,
∴系数最大的项为,且.
练习
方法技巧:
(1)若展开式的系数的绝对值与对应二项式系数相等,可转化为确定二项式系数的最值来解决.
(2)若展开式的系数为的形式,如求的展开式系数最大的项,一般是采用待定系数法,设展开式各项系数分别为,,,,且第项系数最大,应用解出,即得系数最大项.
(3)若展开式的项数较少或转化为讨论较小项的系数的类型,可采用逐个作差(作商)比较确定.
练习
变3.已知展开式中各项的系数和比各项的二项式系数和大992.
(1)求展开式中二项式系数最大的项;
解:令,则二项式各项系数的和为,又展开式中各项的二项式系数之和为,由题意知,.
∴.∴.
∴(舍去)或,∴.
(1)由于为奇数,∴展开式中二项式系数最大的项为中间两项,它们分别是
,.
练习
变3.已知展开式中各项的系数和比各项的二项式系数和大992.
(2)求展开式中系数最大的项.
(2)展开式的通项公式为.
假设项系数最大,则有∴
∴∴,∵,∴.
∴展开式中系数最大的项为.
课堂小结
二项式系数的性质:
1.对称性
与首末两端“等距离”的两个二项式系数相等.事实上,这一性质可直接由
得到.
直线将函数的图象分成对称的两部分,它是图象的对称轴.
2.增减性与最大值
因为,即,
所以,当,即时,随的增加而增大;由对称性知,当
时,随的增加而减小.当是偶数时,中间的一项取得最大值;当是奇数时,中间的两项与相等,且同时取得最大值.
课堂小结
二项式系数的性质:
3.含二项式系数的和
已知,
令,得.
这就是说,的展开式的各二项式系数的和等于.
注:求二项式系数的最大、最小值时,一定要搞清楚是奇数还是偶数.
作业
(1)整理本节课的题型;
(2)课本P34的练习1——4题;
(3)课本P37的复习参考题6的第5题.
直线
6.3.2 二项式系数的性质
问题导入
的展开式的二项式系数有很多有趣的性质,而且我们可以从不同的角度进行研究.
的展开式的二项式系数
1
2
3
4
5
6
问题1:用计算工具计算的展开式的二项式系数,并填入表.
1
1
1
1
2
1
1
3
3
1
1
4
4
6
1
1
5
5
10
10
1
1
6
6
15
15
20
新知探索
从上表中可以发现,每一行中的系数具有对称性.除此之外还有什么规律呢?为了便于发现规律,上表还可以写出如图所示的形式.
观察上图,你还能发现哪些规律?
新知探索
对于的展开式的二项式系数,,,,,我们还可以从函数的角度分析它们.可看成以为自变量的函数,其定义域是.
对于确定的,我们还可以画出它的图象.例如,当时,函数
的图象是7个离散点,如图所示.
新知探索
问题2:(1)观察上图,你发现了什么规律?
(2)请你分别画出时函数的图象,比较它们的异同,你发现了什么规律?
分析上述两个图,可以得到二项式系数的以下性质.
新知探索
1.对称性
与首末两端“等距离”的两个二项式系数相等.事实上,这一性质可直接由
得到.
直线将函数的图象分成对称的两部分,它是图象的对称轴.
2.增减性与最大值
因为,即,
所以,当,即时,随的增加而增大;由对称性知,当
时,随的增加而减小.当是偶数时,中间的一项取得最大值;当是奇数时,中间的两项与相等,且同时取得最大值.
新知探索
3.含二项式系数的和
已知,
令,得.
这就是说,的展开式的各二项式系数的和等于.
新知探索
答案:D.
辨析1.已知的展开式中只有第5项的二项式系数最大,则等于( ).
A.11 B.10 C.9 D.8
辨析2.的展开式中二项展系数最大的项是第_____项.
答案:4或5.
例析
例3.求证:在的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
l
解:在展开式 中,
令,,则得 .
即.
因此,,
即在的展开式中,奇数项的二项式系数的和等于偶数项的二项式系数的和.
练习
题型一:求二项展开式中系数或二项式系数的最大项
例1.(1)的展开式中第6项与第7项的系数相等,则展开式中二项式系数最大的项为( ).
A.第5项 B.第6项或第7项 C.第6项 D.第7项
解:(1),,依题意有.
所以的展开式中,二项式系数最大的项为第5项.故选A.
答案:A.
练习
例1.(2)的展开式中,系数最大的项为( ).
A.第6项 B.第3项 C.第3项或第6项 D.第5项或第7项
解:(2)展开式中,二项式系数与对应的项的系数的绝对值相等.由于二项式系数的最大项为,且中的二项式系数的相反数,此时的系数最小.而,,且.所以系数最大的项为第5项和第7项.故选D.
答案:D.
练习
方法技巧:
(1)根据二项式系数的性质,为奇数时,中间两项的二项式系数最大;为偶数时,中间一项的二项式系数最大.
(2)求展开式中系数最大项与二项式系数最大项是不同的,需根据各项系数的正、负变化情况,一般采用列不等式(组),解不等式(组)的方法求解.一般地,如果第项的系数最大,则与之相邻两项(第项、第项)的系数均不大于第项的系数,由此列不等式组可确定的范围,再根据来确定的值,即可求出最大项.
练习
变1.(1)的展开式中系数最小的项为( ).
A.第6项 B.第7项 C.第8项 D.第9项
解(1):展开式中共有14项,中间两项(第7、8项)的二项式系数最大.由于二项展开式中二项式系数和项的系数满足:奇数项相等,偶数项互为相反数.所以系数最小的项为第8项,系数最大的项为第7项.故选C.
答案:C.
练习
变1.(2)在的展开式中,的系数等于-5,则该展开式的各项的系数中最大值为( ).
A.5 B.10 C.15 D.20
解(2):的展开式的通项,
令,则,所以,即,展开式中第2,4,6项的系数为负数,第1,3,5项的系数为正数,故各项的系数中最大值为.
答案:B.
练习
题型二:求二项展开式的系数和
例2.设
(1)求的值;
(2)求的值;
解:(1)令,得①
(2)令,得②
①②得,
∴.
练习
例2.设
(3)求的值.
解:(3)∵,
∴,.
∴.
练习
方法技巧:
二项展开式中系数和的求法
(1)对形如,的式子求其展开式的各项系数之和,常用赋值法,只需令即可;对的式子求其展开式各项系数之和,只需令即可.
(2)一般地,若,则展开式中各项系数之和为,奇数项系数之和为,偶数项系数之和为.
练习
变2.已知求:
(1);(2)
解:(1)由∵
令,得,
∴.
(2)由(1)得,,①
令得②
所以
练习
题型三:二项式系数性质的应用
例3.已知二项式
(1)若展开式中第5项,第6项,第7项的二项式系数成等差数列,求展开式中二项式系数最大项的系数;
解:(1)由题意,得,∴∴或
①当时,展开式中二项式系数最大的项是和,的系数为,的系数为.
故展开式中二项式系数最大项的系数分别为,.
②当时,展开式中二项式系数最大的项是,
∴的系数为.
故展开式中二项式系数最大项的系数分别为.
练习
例3.已知二项式
(2)若展开式中前三项的二项式系数和等于79,求展开式中系数最大的项.
解:(2)由题意知
解得或(舍去).
设展开式中第项的系数最大,由于,
则解得.
又,∴,
∴系数最大的项为,且.
练习
方法技巧:
(1)若展开式的系数的绝对值与对应二项式系数相等,可转化为确定二项式系数的最值来解决.
(2)若展开式的系数为的形式,如求的展开式系数最大的项,一般是采用待定系数法,设展开式各项系数分别为,,,,且第项系数最大,应用解出,即得系数最大项.
(3)若展开式的项数较少或转化为讨论较小项的系数的类型,可采用逐个作差(作商)比较确定.
练习
变3.已知展开式中各项的系数和比各项的二项式系数和大992.
(1)求展开式中二项式系数最大的项;
解:令,则二项式各项系数的和为,又展开式中各项的二项式系数之和为,由题意知,.
∴.∴.
∴(舍去)或,∴.
(1)由于为奇数,∴展开式中二项式系数最大的项为中间两项,它们分别是
,.
练习
变3.已知展开式中各项的系数和比各项的二项式系数和大992.
(2)求展开式中系数最大的项.
(2)展开式的通项公式为.
假设项系数最大,则有∴
∴∴,∵,∴.
∴展开式中系数最大的项为.
课堂小结
二项式系数的性质:
1.对称性
与首末两端“等距离”的两个二项式系数相等.事实上,这一性质可直接由
得到.
直线将函数的图象分成对称的两部分,它是图象的对称轴.
2.增减性与最大值
因为,即,
所以,当,即时,随的增加而增大;由对称性知,当
时,随的增加而减小.当是偶数时,中间的一项取得最大值;当是奇数时,中间的两项与相等,且同时取得最大值.
课堂小结
二项式系数的性质:
3.含二项式系数的和
已知,
令,得.
这就是说,的展开式的各二项式系数的和等于.
注:求二项式系数的最大、最小值时,一定要搞清楚是奇数还是偶数.
作业
(1)整理本节课的题型;
(2)课本P34的练习1——4题;
(3)课本P37的复习参考题6的第5题.
