高中数学北师大版(2019)必修第二册同步试题:第6章 5-2 平面与平面垂直(含解析)
文档属性
| 名称 | 高中数学北师大版(2019)必修第二册同步试题:第6章 5-2 平面与平面垂直(含解析) |

|
|
| 格式 | zip | ||
| 文件大小 | 369.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-07 00:00:00 | ||
图片预览


文档简介
5.2 平面与平面垂直
必备知识基础练
1.已知一个二面角的两个半平面分别垂直于另一个二面角的两个半平面,若这两个二面角的平面角均为锐角,则这两个二面角的关系是( )
A.相等
B.互补
C.相等或互补
D.既不相等也不互补
2.如图,几何体A-BCDE是一个四棱锥,AB⊥平面BCDE,且四边形BCDE为矩形,则图中互相垂直的平面共有( )
A.4组 B.5组
C.6组 D.7组
3.如图,在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成三棱锥A-BCD,则在三棱锥A-BCD中,下列结论正确的是( )
A.平面ABD⊥平面ABC
B.平面ADC⊥平面BDC
C.平面ABC⊥平面BDC
D.平面ADC⊥平面ABC
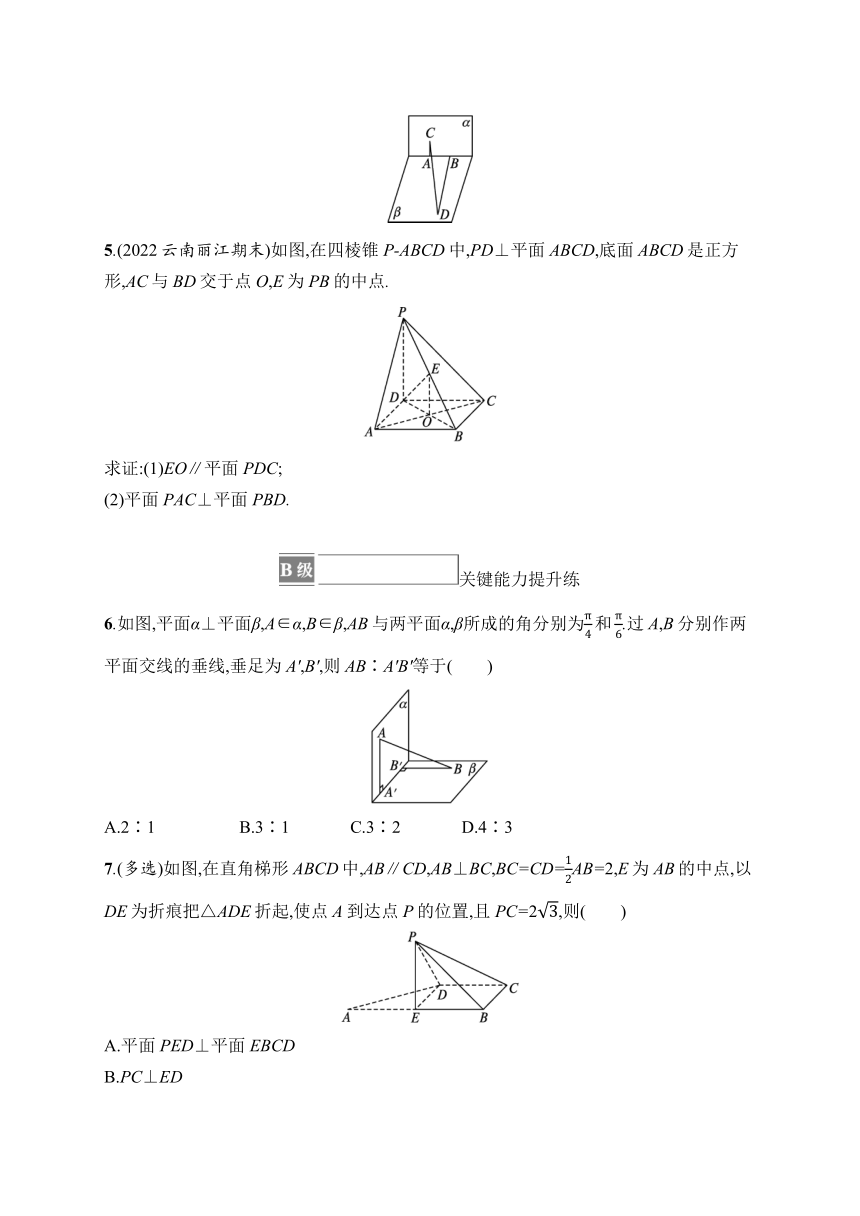
4.如图,已知平面α⊥平面β,在α与β的交线上取线段AB=4 cm,AC,BD分别在平面α和平面β内,它们都垂直于交线AB,并且AC=3 cm,BD=12 cm,则BC= cm,
CD= cm.
5.(2022云南丽江期末)如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是正方形,AC与BD交于点O,E为PB的中点.
求证:(1)EO∥平面PDC;
(2)平面PAC⊥平面PBD.
关键能力提升练
6.如图,平面α⊥平面β,A∈α,B∈β,AB与两平面α,β所成的角分别为.过A,B分别作两平面交线的垂线,垂足为A',B',则AB∶A'B'等于( )
A.2∶1 B.3∶1 C.3∶2 D.4∶3
7.(多选)如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,BC=CD=AB=2,E为AB的中点,以DE为折痕把△ADE折起,使点A到达点P的位置,且PC=2,则( )
A.平面PED⊥平面EBCD
B.PC⊥ED
C.二面角P-DC-B的大小为
D.PC与平面PED所成角的正切值为
8.如图所示,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥平面ABCD,且SA=AB,点E为AB的中点,点F为SC的中点.
(1)求证:EF⊥CD;
(2)求证:平面SCD⊥平面SCE.
学科素养创新练
9.图1是由矩形ADEB,Rt△ABC和菱形BFGC组成的一个平面图形,其中AB=1,BE=BF=2,∠FBC=60°.将其沿AB,BC折起使得BE与BF重合,连接DG,如图2.
(1)证明:图2中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;
(2)求图2中的四边形ACGD的面积.
答案
1.A 画图(图略)易得到满足已知条件的两个二面角相等或互补,若它们的平面角均为锐角,则这两个二面角相等.
2.C 因为AB⊥平面BCDE,AB 平面ABC,AB 平面ABD,AB 平面ABE,
所以平面ABC⊥平面BCDE,平面ABD⊥平面BCDE,平面ABE⊥平面BCDE,
又因为四边形BCDE为矩形,所以BC⊥平面ABE 平面ABC⊥平面ABE,
同理可得平面ACD⊥平面ABC,平面ADE⊥平面ABE.
故图中互相垂直的平面共有6组.
3.D 由已知得BA⊥AD,CD⊥BD,
又平面ABD⊥平面BCD,
平面ABD∩平面BCD=BD,
所以CD⊥平面ABD,从而CD⊥AB,故AB⊥平面ADC.
又AB 平面ABC,所以平面ABC⊥平面ADC.
4.5 13 连接BC.因为α⊥β,α∩β=AB,BD⊥AB,
所以BD⊥平面α.
因为BC 平面α,所以BD⊥BC.
在Rt△BAC中,
BC==5,
在Rt△DBC中,CD==13.
5.证明(1)∵底面ABCD是正方形,AC与BD交于点O,
∴O为BD中点.
又E为PB的中点,∴EO∥PD.
∵EO 平面PDC,PD 平面PDC,∴EO∥平面PDC.
(2)∵底面ABCD是正方形,∴AC⊥BD.
又PD⊥平面ABCD,AC 平面ABCD,∴PD⊥AC.
∵PD∩BD=D,∴AC⊥平面PBD.
又AC 平面PAC,
∴平面PAC⊥平面PBD.
6.A 由已知条件可知∠BAB'=,∠ABA'=.
设AB=2a,则BB'=2asina,A'B=2acosa,
∴在Rt△BB'A'中,得A'B'=a,∴AB∶A'B'=2∶1.
7.AC PD=AD==2,在△PDC中,PD2+CD2=PC2,所以PD⊥CD.易知CD⊥DE.又PD∩DE=D,所以CD⊥平面PED.又CD 平面EBCD,所以平面PED⊥平面EBCD,故A选项正确;
若PC⊥ED,由ED⊥CD,可得ED⊥平面PDC,则ED⊥PD,而∠EDP=∠EDA=,显然矛盾,故B选项错误;
二面角P-DC-B的平面角为∠PDE,易知∠PDE=∠ADE=,故选项C正确;
由上面分析可知,∠CPD为直线PC与平面PED所成的角.
在Rt△PCD中,tan∠CPD=,故D选项错误.
8.证明(1)连接AC,AF,BF,
因为SA⊥平面ABCD,
所以AF为Rt△SAC斜边SC上的中线,所以AF=SC.
又因为四边形ABCD是正方形,所以CB⊥AB.
而由SA⊥平面ABCD,得CB⊥SA,
所以CB⊥平面SAB,所以CB⊥SB,
所以BF为Rt△SBC斜边SC上的中线,
所以BF=SC,所以△AFB为等腰三角形.
因为E为AB的中点,所以EF⊥AB.
又CD∥AB,所以EF⊥CD.
(2)由已知易得Rt△SAE≌Rt△CBE,
所以SE=EC,即△SEC是等腰三角形,所以EF⊥SC.
又因为EF⊥CD,SC∩CD=C,所以EF⊥平面SCD.
又EF 平面SCE,
所以平面SCD⊥平面SCE.
9.(1)证明由已知得AD∥BE,CG∥BE,所以AD∥CG,
故AD,CG确定一个平面,从而A,C,G,D四点共面.
由已知得AB⊥BE,AB⊥BC,故AB⊥平面BCGE.
又因为AB 平面ABC,
所以平面ABC⊥平面BCGE.
(2)解取CG的中点M,连接EM,DM.因为AB∥DE,AB⊥平面BCGE,所以DE⊥平面BCGE,
故DE⊥CG.
由已知,四边形BCGE是菱形,且∠EBC=60°得EM⊥CG,故CG⊥平面DEM.
因此DM⊥CG.在Rt△DEM中,DE=1,EM=,
必备知识基础练
1.已知一个二面角的两个半平面分别垂直于另一个二面角的两个半平面,若这两个二面角的平面角均为锐角,则这两个二面角的关系是( )
A.相等
B.互补
C.相等或互补
D.既不相等也不互补
2.如图,几何体A-BCDE是一个四棱锥,AB⊥平面BCDE,且四边形BCDE为矩形,则图中互相垂直的平面共有( )
A.4组 B.5组
C.6组 D.7组
3.如图,在四边形ABCD中,AD∥BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成三棱锥A-BCD,则在三棱锥A-BCD中,下列结论正确的是( )
A.平面ABD⊥平面ABC
B.平面ADC⊥平面BDC
C.平面ABC⊥平面BDC
D.平面ADC⊥平面ABC
4.如图,已知平面α⊥平面β,在α与β的交线上取线段AB=4 cm,AC,BD分别在平面α和平面β内,它们都垂直于交线AB,并且AC=3 cm,BD=12 cm,则BC= cm,
CD= cm.
5.(2022云南丽江期末)如图,在四棱锥P-ABCD中,PD⊥平面ABCD,底面ABCD是正方形,AC与BD交于点O,E为PB的中点.
求证:(1)EO∥平面PDC;
(2)平面PAC⊥平面PBD.
关键能力提升练
6.如图,平面α⊥平面β,A∈α,B∈β,AB与两平面α,β所成的角分别为.过A,B分别作两平面交线的垂线,垂足为A',B',则AB∶A'B'等于( )
A.2∶1 B.3∶1 C.3∶2 D.4∶3
7.(多选)如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,BC=CD=AB=2,E为AB的中点,以DE为折痕把△ADE折起,使点A到达点P的位置,且PC=2,则( )
A.平面PED⊥平面EBCD
B.PC⊥ED
C.二面角P-DC-B的大小为
D.PC与平面PED所成角的正切值为
8.如图所示,在四棱锥S-ABCD中,底面ABCD是正方形,SA⊥平面ABCD,且SA=AB,点E为AB的中点,点F为SC的中点.
(1)求证:EF⊥CD;
(2)求证:平面SCD⊥平面SCE.
学科素养创新练
9.图1是由矩形ADEB,Rt△ABC和菱形BFGC组成的一个平面图形,其中AB=1,BE=BF=2,∠FBC=60°.将其沿AB,BC折起使得BE与BF重合,连接DG,如图2.
(1)证明:图2中的A,C,G,D四点共面,且平面ABC⊥平面BCGE;
(2)求图2中的四边形ACGD的面积.
答案
1.A 画图(图略)易得到满足已知条件的两个二面角相等或互补,若它们的平面角均为锐角,则这两个二面角相等.
2.C 因为AB⊥平面BCDE,AB 平面ABC,AB 平面ABD,AB 平面ABE,
所以平面ABC⊥平面BCDE,平面ABD⊥平面BCDE,平面ABE⊥平面BCDE,
又因为四边形BCDE为矩形,所以BC⊥平面ABE 平面ABC⊥平面ABE,
同理可得平面ACD⊥平面ABC,平面ADE⊥平面ABE.
故图中互相垂直的平面共有6组.
3.D 由已知得BA⊥AD,CD⊥BD,
又平面ABD⊥平面BCD,
平面ABD∩平面BCD=BD,
所以CD⊥平面ABD,从而CD⊥AB,故AB⊥平面ADC.
又AB 平面ABC,所以平面ABC⊥平面ADC.
4.5 13 连接BC.因为α⊥β,α∩β=AB,BD⊥AB,
所以BD⊥平面α.
因为BC 平面α,所以BD⊥BC.
在Rt△BAC中,
BC==5,
在Rt△DBC中,CD==13.
5.证明(1)∵底面ABCD是正方形,AC与BD交于点O,
∴O为BD中点.
又E为PB的中点,∴EO∥PD.
∵EO 平面PDC,PD 平面PDC,∴EO∥平面PDC.
(2)∵底面ABCD是正方形,∴AC⊥BD.
又PD⊥平面ABCD,AC 平面ABCD,∴PD⊥AC.
∵PD∩BD=D,∴AC⊥平面PBD.
又AC 平面PAC,
∴平面PAC⊥平面PBD.
6.A 由已知条件可知∠BAB'=,∠ABA'=.
设AB=2a,则BB'=2asina,A'B=2acosa,
∴在Rt△BB'A'中,得A'B'=a,∴AB∶A'B'=2∶1.
7.AC PD=AD==2,在△PDC中,PD2+CD2=PC2,所以PD⊥CD.易知CD⊥DE.又PD∩DE=D,所以CD⊥平面PED.又CD 平面EBCD,所以平面PED⊥平面EBCD,故A选项正确;
若PC⊥ED,由ED⊥CD,可得ED⊥平面PDC,则ED⊥PD,而∠EDP=∠EDA=,显然矛盾,故B选项错误;
二面角P-DC-B的平面角为∠PDE,易知∠PDE=∠ADE=,故选项C正确;
由上面分析可知,∠CPD为直线PC与平面PED所成的角.
在Rt△PCD中,tan∠CPD=,故D选项错误.
8.证明(1)连接AC,AF,BF,
因为SA⊥平面ABCD,
所以AF为Rt△SAC斜边SC上的中线,所以AF=SC.
又因为四边形ABCD是正方形,所以CB⊥AB.
而由SA⊥平面ABCD,得CB⊥SA,
所以CB⊥平面SAB,所以CB⊥SB,
所以BF为Rt△SBC斜边SC上的中线,
所以BF=SC,所以△AFB为等腰三角形.
因为E为AB的中点,所以EF⊥AB.
又CD∥AB,所以EF⊥CD.
(2)由已知易得Rt△SAE≌Rt△CBE,
所以SE=EC,即△SEC是等腰三角形,所以EF⊥SC.
又因为EF⊥CD,SC∩CD=C,所以EF⊥平面SCD.
又EF 平面SCE,
所以平面SCD⊥平面SCE.
9.(1)证明由已知得AD∥BE,CG∥BE,所以AD∥CG,
故AD,CG确定一个平面,从而A,C,G,D四点共面.
由已知得AB⊥BE,AB⊥BC,故AB⊥平面BCGE.
又因为AB 平面ABC,
所以平面ABC⊥平面BCGE.
(2)解取CG的中点M,连接EM,DM.因为AB∥DE,AB⊥平面BCGE,所以DE⊥平面BCGE,
故DE⊥CG.
由已知,四边形BCGE是菱形,且∠EBC=60°得EM⊥CG,故CG⊥平面DEM.
因此DM⊥CG.在Rt△DEM中,DE=1,EM=,
同课章节目录
- 第一章 三角函数
- 1 周期变化
- 2 任意角
- 3 弧度制
- 4 正弦函数和余弦函数的概念及其性质
- 5 正弦函数、余弦函数的图象与性质再认识
- 6 函数y=Asin(wx+φ)性质与图象
- 7 正切函数
- 8 三角函数的简单应用
- 第二章 平面向量及其应用
- 1 从位移、速度、力到向量
- 2 从位移的合成到向量的加减法
- 3 从速度的倍数到向量的数乘
- 4 平面向量基本定理及坐标表示
- 5 从力的做功到向量的数量积
- 6 平面向量的应用
- 第三章 数学建模活动(二)
- 1 建筑物高度的测量
- 2 测量和自选建模作业的汇报交流
- 第四章 三角恒等变换
- 1 同角三角函数的基本关系
- 2 两角和与差的三角函数公式
- 3 二倍角的三角函数公式
- 第五章 复数
- 1 复数的概念及其几何意义
- 2 复数的四则运算
- 3 复数的三角表示
- 第六章 立体几何初步
- 1 基本立体图形
- 2 直观图
- 3 空间点、直线、平面之间的位置关系
- 4 平行关系
- 5 垂直关系
- 6 简单几何体的再认识
