5.2.3++简单复合函数的导数+课件-2022-2023学年高二下学期数学人教A版(2019)选择性必修第二册(共15张PPT)
文档属性
| 名称 | 5.2.3++简单复合函数的导数+课件-2022-2023学年高二下学期数学人教A版(2019)选择性必修第二册(共15张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 31.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-07 14:46:32 | ||
图片预览






文档简介
(共15张PPT)
5.2.3简单复合函数的导数
5.2 导数的运算
思 考
如何求函数的导数呢?
=
的导数呢?
提示:设 ,从而可以看作是两个函数“复合”得到的,.
复合函数
一般地,对于两个函数y=f(u)和u=g(x),如果通过中间变量u,y可以表示成x的函数,那么称这个函数为函数y=f(u)和u=g(x)的复合函数,记作y=f(g(x)).
新 知
例 求函数.
解:令, .
解: 令,得
以表示对的导数,表示对的导数,
一方面, =
=2
2
另一方面 = , =2
可以发现
例1 求函数.
复合函数求导法则:
一般地,对于由函数y=f(u)和u=g(x)复合而成的函数y=f(g(x)),它的导数与函数y=f(u),u=g(x)的导数间的关系为 即y对x的导数等于y对u的导数与u对x 的导数的乘积.
注:(1)函数y=f(u)和u=g(x)通常为基本初等函数;
(2)求导时分清是对哪个变量求导;
(3)计算结果尽量简洁.
新 知
( )
( )
( )
( )
√
√
×
×
判 断
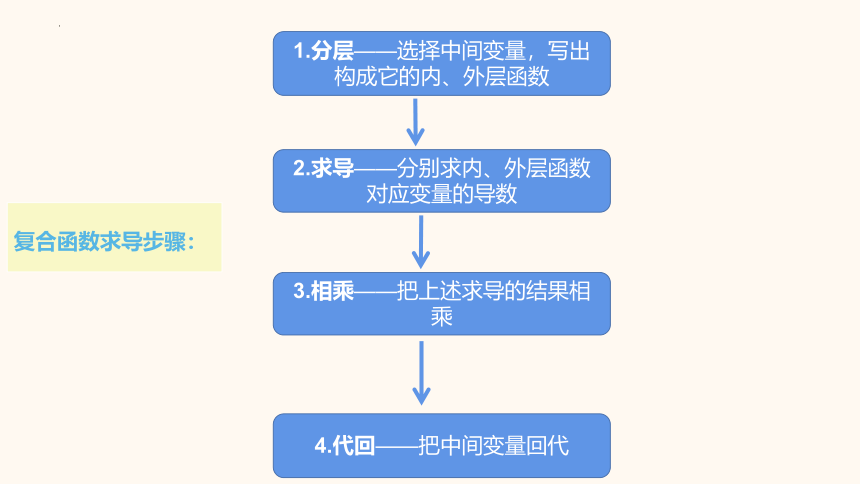
复合函数求导步骤:
1.分层——选择中间变量,写出构成它的内、外层函数
2.求导——分别求内、外层函数对应变量的导数
3.相乘——把上述求导的结果相乘
4.代回——把中间变量回代
(1)函数 可以看作函数 的复合函数.根据复合函数的求导法则,有
解:
(2)函数 可以看作函数 的复合函数.根据复合函数的求导法则,有
(3)函数 可以看作函数 和 的复合函数.根据复合函数的求导法则,有
例2 求下列函数的导数:
(1) (2) (3)
例3 某个弹簧振子在振动过程中的位移y(单位:mm)关于时间t(单位:s)的函数满足关系式为 . 求函数y在t=3s 时的导数,并解释它的实际意义.
函数可以看作函数 和 的复合函数.根据复合函数的求导法则,有
当 t=3 时,
它表示当t=3 s 时,弹簧振子振动的瞬时速度为0 mm/s .
解:
(3) (4)
(5) (6)
练习 求导
(1) (2)
(2)
(3)
(4)
(5)
(6)
(1)
解:
练习
1. 已知函数 ,若,则__________ .
2.设函数 f(x) 的导函数是 ,若 ,则 ______ .
3. 已知函数 为可导的偶函数,(c为常数),
若,则______ .
1
-2
-
总 结
分层——选择中间变量,写出构成它的内、外层函数
求导——分别求内、外层函数对应变量的导数
相乘——把上述求导的结果相乘
代回——把中间变量回代
复合函数求导
复合函数
对于两个函数y=f(u)和u=g(x),如果通过中间变量u,y可以表示成x的函数,那么称这个函数为函数y=f(u)和u=g(x)的复合函数,记作y=f(g(x)). 且 .
课后提升
1.下列求导运算正确的是( )A. B. C. D.
2.函数在处的切线方程为( )A. B. C. D.
3.已知函数 ,则( )
A. B. C. D.
4.若曲线在点(1,0)处的切线与直线 平行,则( )A.0 B.1 C.2 D.3
B
C
A
D
5.已知函数 .
(1)求的导数.
(2)求曲线在点(1,0)处的切线方程,并求出切线与坐标轴所围三角形的面积.
课后提升
解(1)因为 ,所以 ,
当时,;当时,.
故切线与坐标轴所围三角形的面积 .
(2)由(1)得, ,则所求切线的斜率为1,故所求切线方程为,
【分析】(1)利用导数的除法运算法则进行求解即可;
(2)先利用导数求出切线的斜率,然后用点斜式即可求解,求得截距,利用三角形面积公式可得答案.
5.2.3简单复合函数的导数
5.2 导数的运算
思 考
如何求函数的导数呢?
=
的导数呢?
提示:设 ,从而可以看作是两个函数“复合”得到的,.
复合函数
一般地,对于两个函数y=f(u)和u=g(x),如果通过中间变量u,y可以表示成x的函数,那么称这个函数为函数y=f(u)和u=g(x)的复合函数,记作y=f(g(x)).
新 知
例 求函数.
解:令, .
解: 令,得
以表示对的导数,表示对的导数,
一方面, =
=2
2
另一方面 = , =2
可以发现
例1 求函数.
复合函数求导法则:
一般地,对于由函数y=f(u)和u=g(x)复合而成的函数y=f(g(x)),它的导数与函数y=f(u),u=g(x)的导数间的关系为 即y对x的导数等于y对u的导数与u对x 的导数的乘积.
注:(1)函数y=f(u)和u=g(x)通常为基本初等函数;
(2)求导时分清是对哪个变量求导;
(3)计算结果尽量简洁.
新 知
( )
( )
( )
( )
√
√
×
×
判 断
复合函数求导步骤:
1.分层——选择中间变量,写出构成它的内、外层函数
2.求导——分别求内、外层函数对应变量的导数
3.相乘——把上述求导的结果相乘
4.代回——把中间变量回代
(1)函数 可以看作函数 的复合函数.根据复合函数的求导法则,有
解:
(2)函数 可以看作函数 的复合函数.根据复合函数的求导法则,有
(3)函数 可以看作函数 和 的复合函数.根据复合函数的求导法则,有
例2 求下列函数的导数:
(1) (2) (3)
例3 某个弹簧振子在振动过程中的位移y(单位:mm)关于时间t(单位:s)的函数满足关系式为 . 求函数y在t=3s 时的导数,并解释它的实际意义.
函数可以看作函数 和 的复合函数.根据复合函数的求导法则,有
当 t=3 时,
它表示当t=3 s 时,弹簧振子振动的瞬时速度为0 mm/s .
解:
(3) (4)
(5) (6)
练习 求导
(1) (2)
(2)
(3)
(4)
(5)
(6)
(1)
解:
练习
1. 已知函数 ,若,则__________ .
2.设函数 f(x) 的导函数是 ,若 ,则 ______ .
3. 已知函数 为可导的偶函数,(c为常数),
若,则______ .
1
-2
-
总 结
分层——选择中间变量,写出构成它的内、外层函数
求导——分别求内、外层函数对应变量的导数
相乘——把上述求导的结果相乘
代回——把中间变量回代
复合函数求导
复合函数
对于两个函数y=f(u)和u=g(x),如果通过中间变量u,y可以表示成x的函数,那么称这个函数为函数y=f(u)和u=g(x)的复合函数,记作y=f(g(x)). 且 .
课后提升
1.下列求导运算正确的是( )A. B. C. D.
2.函数在处的切线方程为( )A. B. C. D.
3.已知函数 ,则( )
A. B. C. D.
4.若曲线在点(1,0)处的切线与直线 平行,则( )A.0 B.1 C.2 D.3
B
C
A
D
5.已知函数 .
(1)求的导数.
(2)求曲线在点(1,0)处的切线方程,并求出切线与坐标轴所围三角形的面积.
课后提升
解(1)因为 ,所以 ,
当时,;当时,.
故切线与坐标轴所围三角形的面积 .
(2)由(1)得, ,则所求切线的斜率为1,故所求切线方程为,
【分析】(1)利用导数的除法运算法则进行求解即可;
(2)先利用导数求出切线的斜率,然后用点斜式即可求解,求得截距,利用三角形面积公式可得答案.
