2022-2023学年苏科版九年级下册5.5 用二次函数解决问题 随堂作业 (无答案)
文档属性
| 名称 | 2022-2023学年苏科版九年级下册5.5 用二次函数解决问题 随堂作业 (无答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 977.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-08 16:36:18 | ||
图片预览



文档简介
5.5 用二次函数解决问题(随堂作业)-苏科版九年级下册
一.选择题
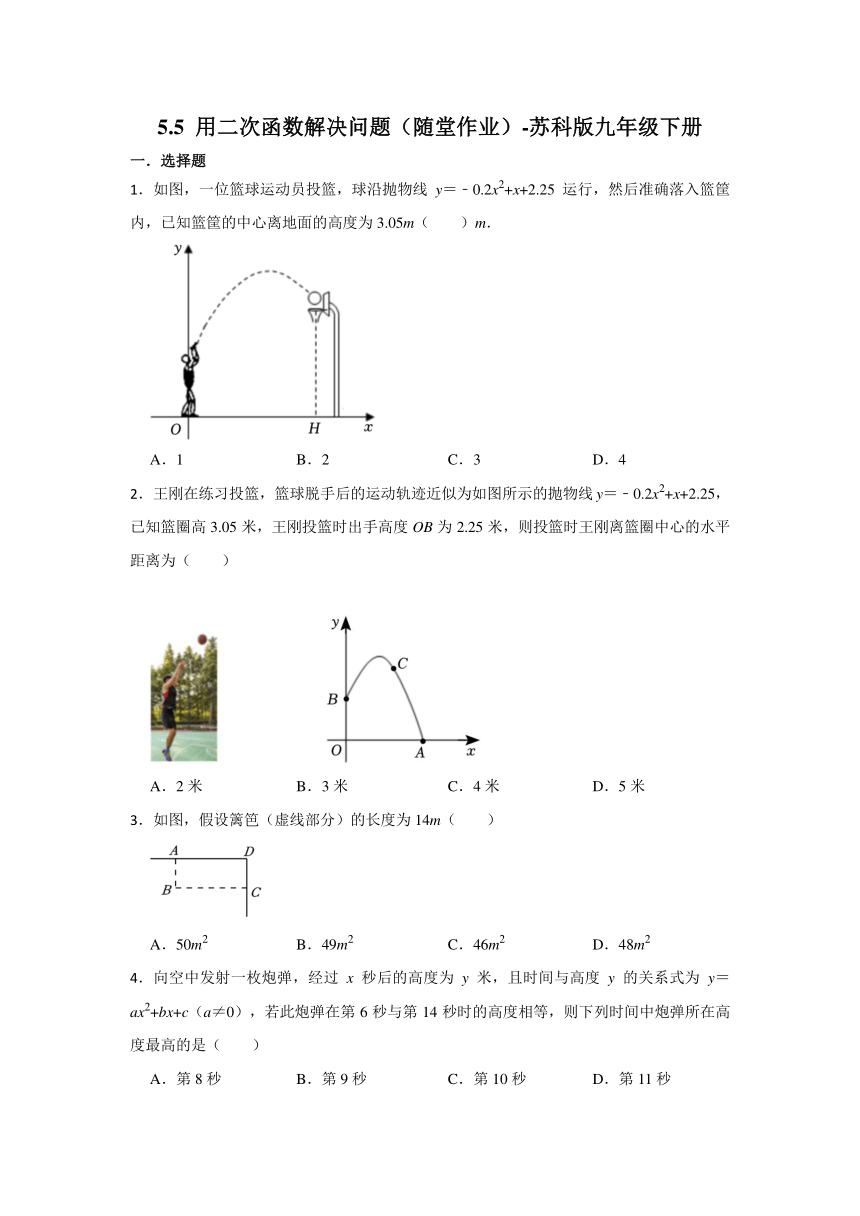
.如图,一位篮球运动员投篮,球沿抛物线y=﹣0.2x2+x+2.25运行,然后准确落入篮筐内,已知篮筐的中心离地面的高度为3.05m( )m.
A.1 B.2 C.3 D.4
.王刚在练习投篮,篮球脱手后的运动轨迹近似为如图所示的抛物线y=﹣0.2x2+x+2.25,已知篮圈高3.05米,王刚投篮时出手高度OB为2.25米,则投篮时王刚离篮圈中心的水平距离为( )
A.2米 B.3米 C.4米 D.5米
.如图,假设篱笆(虚线部分)的长度为14m( )
A.50m2 B.49m2 C.46m2 D.48m2
.向空中发射一枚炮弹,经过x秒后的高度为y米,且时间与高度y的关系式为y=ax2+bx+c(a≠0),若此炮弹在第6秒与第14秒时的高度相等,则下列时间中炮弹所在高度最高的是( )
A.第8秒 B.第9秒 C.第10秒 D.第11秒
.如图,一座拱桥的纵向截面是抛物线的一部分,拱桥的跨度为4.9m,拱顶离水面2m,如图,抛物线的对称轴为y轴,建立平面直角坐标系( )
A.y=﹣2.45x2 B.y=﹣2x2 C. D.
从地面竖直向上抛出一小球,小球的高度h(米)与运动时间t(秒)2+30t(0≤t≤6),则小球到达最高高度时,运动的时间是( )
A.1秒 B.2秒 C.3秒 D.4秒
.从高处自由下落的物体,下落距离s与下落时间t的平方成正比.若某一物体从125米高度自由下落,5秒落地,距离地面的高度为( )
A.5米 B.25米 C.100米 D.120米
.如图,一位运动员推铅球,铅球运行高度y(m)(m)之间的函数关系式是y=﹣.问:此运动员能把铅球推出多远?( )
A.12m B.10m C.3m D.4m
如图,在水平地面点A处有一网球发射器向空中发射网球,网球在地面上的落点为B,小明在直线AB上点C(靠点B一侧)右侧竖直向上摆放若干个无盖的、直径为0.5米(网球的体积和圆柱形桶的厚度忽略不计).已知AB=4米,AC=3米,若要使网球能落入桶内,则至少需摆放圆柱形桶( )
A.4个 B.5个 C.6个 D.7个
下面的三个问题中都有两个变量:
①汽车从A地匀速行驶到B地,汽车的剩余路程y与行驶时间x;
②将水箱中的水匀速放出,直至放完,水箱中的剩余水量y与放水时间x;
③用长度一定的绳子围成一个矩形,矩形的面积y与一边长x;
其中,变量y与变量x之间的函数关系可以利用如图所示的图象表示的是( )
A.①② B.①③ C.②③ D.①④
二.填空题
.从地面竖直向上跑出一小球,小球的高度h(单位:m)与小球的运动时间t(单位:s)2(0≤t≤6).小球运动到 s时,达到最大高度 .
.2019年在武汉市举行了军运会.在军运会比赛中,某次羽毛球的运动路线可以看作是抛物线的一部分(如图),球落地点A到O点的距离是 .
.商店销售一种进价为20元/个的帽子,经调查发现,该种帽子每天的销售量w(个)(元)满足w=﹣2x+80(20≤x≤40),设销售这种帽子每天的利润为y(元) ;当销售单价定为 元时,每天的利润最大.
.如图,两条钢缆具有相同的抛物线形状.按照图中的直角坐标系,左面的一条抛物线可以用y=0.0225x2+0.9x+10表示,而且左右两条抛物线关于y轴对称,右边的抛物线解析式是 .
.某游乐场的圆形喷水池中心O有一雕塑OA,从A点向四周喷水,喷出的水柱为抛物线,以水平方向为x轴,点O为原点建立直角坐标系,x轴上的点C,D为水柱的落水点(x﹣5)2+6,则CD的长为 m.
三.解答题
.某品牌保温杯专卖店平均每天可售出20个,每个盈利40元.为了扩大销售、增加盈利,该专卖店采取了降价措施,发现销售单价每降低1元,平均每天可多售出2个.
(1)若降价3元,则该专卖店平均每天售出保温杯 个;
(2)当每个保温杯降价多少元时,该专卖店每天销售利润最大,最大利润是多少元?
.如图,王大爷准备围一块菜地,菜地一面靠墙,另外三面用29米长的篱笆围成,其中一面开一扇1米宽的门(不包括篱笆).
(1)王大爷能否围成面积为100平方米的菜地?若能,求BC的长;若不能.请说明理由.
(2)王大爷想要围成的菜地面积最大,请你帮助他设计一下.
.如图,有长为30m的篱笆,一面利用墙(墙的最大可用长度为10m)(平行于AB)的长方形花圃.
(1)设花圃的一边AB为xm,花圃的面积为Sm2,请写出S与x的函数关系式,以及自变量x的取值范围;
(2)当AB的长是多少米时,围成的花圃面积为63平方米?
(3)能围成比63平方米更大的花圃吗?如果能,请求出最大的面积.如果不能,请说明理由.
.实心球是北京市初中体育学业水平现场考试选考项目之一,某同学作了2次实心球训练.第一次训练中实心球行进路线是一条抛物线,行进高度y(m)(m)之间的函数关系如图所示,掷出时起点处高度为1.6m,实心球行进至最高点3.4m处.
(1)求y关于x的函数表达式;
(2)该同学第二次训练实心球的竖直高度y与水平距离x近似满足函数关系:y=﹣0.125(x﹣4)2+3.6,记第一次实心球从起点到落地点的水平距离为d1,第二次实心球从起点到落地点的水平距离为d2,则d1 d2.(填“>”“=”或“<”).
.为了在校运动会的推铅球项目中取得更好的成绩,小石积极训练,铅球被推出后的飞行路线可以看作是抛物线的一部分.建立如图所示的平面直角坐标系(点A处)到落地的过程中,铅球的竖直高度y(单位:m)(单位:m)近似满足函数关系y=a(x﹣h)2+k(a<0).
小石进行了两次训练.
(1)第一次训练时,铅球的水平距离x与竖直高度y的几组数据如下:
水平距离 x/m 0 1 2 3 4 5 6 7 8
竖直高度 y/m 1.6 2.1 2.4 2.5 2.4 2.1 1.6 0.9 0
根据上述数据,求出满足的函数关系y=a(x﹣h)2+k(a<0),并直接写出小石此次训练的成绩(铅球落地点的水平距离);
(2)第二次训练时,小石推出的铅球的竖直高度y与水平距离x近似满足函数关系y=﹣0.09(x﹣3.1)2+2.55.记小石第一次训练的成绩为d1,第二次训练的成绩为d2,则d1 d2(填“>”,“=”或“<”).
一.选择题
.如图,一位篮球运动员投篮,球沿抛物线y=﹣0.2x2+x+2.25运行,然后准确落入篮筐内,已知篮筐的中心离地面的高度为3.05m( )m.
A.1 B.2 C.3 D.4
.王刚在练习投篮,篮球脱手后的运动轨迹近似为如图所示的抛物线y=﹣0.2x2+x+2.25,已知篮圈高3.05米,王刚投篮时出手高度OB为2.25米,则投篮时王刚离篮圈中心的水平距离为( )
A.2米 B.3米 C.4米 D.5米
.如图,假设篱笆(虚线部分)的长度为14m( )
A.50m2 B.49m2 C.46m2 D.48m2
.向空中发射一枚炮弹,经过x秒后的高度为y米,且时间与高度y的关系式为y=ax2+bx+c(a≠0),若此炮弹在第6秒与第14秒时的高度相等,则下列时间中炮弹所在高度最高的是( )
A.第8秒 B.第9秒 C.第10秒 D.第11秒
.如图,一座拱桥的纵向截面是抛物线的一部分,拱桥的跨度为4.9m,拱顶离水面2m,如图,抛物线的对称轴为y轴,建立平面直角坐标系( )
A.y=﹣2.45x2 B.y=﹣2x2 C. D.
从地面竖直向上抛出一小球,小球的高度h(米)与运动时间t(秒)2+30t(0≤t≤6),则小球到达最高高度时,运动的时间是( )
A.1秒 B.2秒 C.3秒 D.4秒
.从高处自由下落的物体,下落距离s与下落时间t的平方成正比.若某一物体从125米高度自由下落,5秒落地,距离地面的高度为( )
A.5米 B.25米 C.100米 D.120米
.如图,一位运动员推铅球,铅球运行高度y(m)(m)之间的函数关系式是y=﹣.问:此运动员能把铅球推出多远?( )
A.12m B.10m C.3m D.4m
如图,在水平地面点A处有一网球发射器向空中发射网球,网球在地面上的落点为B,小明在直线AB上点C(靠点B一侧)右侧竖直向上摆放若干个无盖的、直径为0.5米(网球的体积和圆柱形桶的厚度忽略不计).已知AB=4米,AC=3米,若要使网球能落入桶内,则至少需摆放圆柱形桶( )
A.4个 B.5个 C.6个 D.7个
下面的三个问题中都有两个变量:
①汽车从A地匀速行驶到B地,汽车的剩余路程y与行驶时间x;
②将水箱中的水匀速放出,直至放完,水箱中的剩余水量y与放水时间x;
③用长度一定的绳子围成一个矩形,矩形的面积y与一边长x;
其中,变量y与变量x之间的函数关系可以利用如图所示的图象表示的是( )
A.①② B.①③ C.②③ D.①④
二.填空题
.从地面竖直向上跑出一小球,小球的高度h(单位:m)与小球的运动时间t(单位:s)2(0≤t≤6).小球运动到 s时,达到最大高度 .
.2019年在武汉市举行了军运会.在军运会比赛中,某次羽毛球的运动路线可以看作是抛物线的一部分(如图),球落地点A到O点的距离是 .
.商店销售一种进价为20元/个的帽子,经调查发现,该种帽子每天的销售量w(个)(元)满足w=﹣2x+80(20≤x≤40),设销售这种帽子每天的利润为y(元) ;当销售单价定为 元时,每天的利润最大.
.如图,两条钢缆具有相同的抛物线形状.按照图中的直角坐标系,左面的一条抛物线可以用y=0.0225x2+0.9x+10表示,而且左右两条抛物线关于y轴对称,右边的抛物线解析式是 .
.某游乐场的圆形喷水池中心O有一雕塑OA,从A点向四周喷水,喷出的水柱为抛物线,以水平方向为x轴,点O为原点建立直角坐标系,x轴上的点C,D为水柱的落水点(x﹣5)2+6,则CD的长为 m.
三.解答题
.某品牌保温杯专卖店平均每天可售出20个,每个盈利40元.为了扩大销售、增加盈利,该专卖店采取了降价措施,发现销售单价每降低1元,平均每天可多售出2个.
(1)若降价3元,则该专卖店平均每天售出保温杯 个;
(2)当每个保温杯降价多少元时,该专卖店每天销售利润最大,最大利润是多少元?
.如图,王大爷准备围一块菜地,菜地一面靠墙,另外三面用29米长的篱笆围成,其中一面开一扇1米宽的门(不包括篱笆).
(1)王大爷能否围成面积为100平方米的菜地?若能,求BC的长;若不能.请说明理由.
(2)王大爷想要围成的菜地面积最大,请你帮助他设计一下.
.如图,有长为30m的篱笆,一面利用墙(墙的最大可用长度为10m)(平行于AB)的长方形花圃.
(1)设花圃的一边AB为xm,花圃的面积为Sm2,请写出S与x的函数关系式,以及自变量x的取值范围;
(2)当AB的长是多少米时,围成的花圃面积为63平方米?
(3)能围成比63平方米更大的花圃吗?如果能,请求出最大的面积.如果不能,请说明理由.
.实心球是北京市初中体育学业水平现场考试选考项目之一,某同学作了2次实心球训练.第一次训练中实心球行进路线是一条抛物线,行进高度y(m)(m)之间的函数关系如图所示,掷出时起点处高度为1.6m,实心球行进至最高点3.4m处.
(1)求y关于x的函数表达式;
(2)该同学第二次训练实心球的竖直高度y与水平距离x近似满足函数关系:y=﹣0.125(x﹣4)2+3.6,记第一次实心球从起点到落地点的水平距离为d1,第二次实心球从起点到落地点的水平距离为d2,则d1 d2.(填“>”“=”或“<”).
.为了在校运动会的推铅球项目中取得更好的成绩,小石积极训练,铅球被推出后的飞行路线可以看作是抛物线的一部分.建立如图所示的平面直角坐标系(点A处)到落地的过程中,铅球的竖直高度y(单位:m)(单位:m)近似满足函数关系y=a(x﹣h)2+k(a<0).
小石进行了两次训练.
(1)第一次训练时,铅球的水平距离x与竖直高度y的几组数据如下:
水平距离 x/m 0 1 2 3 4 5 6 7 8
竖直高度 y/m 1.6 2.1 2.4 2.5 2.4 2.1 1.6 0.9 0
根据上述数据,求出满足的函数关系y=a(x﹣h)2+k(a<0),并直接写出小石此次训练的成绩(铅球落地点的水平距离);
(2)第二次训练时,小石推出的铅球的竖直高度y与水平距离x近似满足函数关系y=﹣0.09(x﹣3.1)2+2.55.记小石第一次训练的成绩为d1,第二次训练的成绩为d2,则d1 d2(填“>”,“=”或“<”).
同课章节目录
- 第5章 二次函数
- 5.1 二次函数
- 5.2 二次函数的图象和性质
- 5.3 用待定系数法确定二次函数表达式
- 5.4 二次函数与一元二次方程
- 5.5 用二次函数解决问题
- 第6章 图形的相似
- 6.1 图上距离与实际距离
- 6.2 黄金分割
- 6.3 相似图形
- 6.4 探索三角形相似的条件
- 6.5 相似三角形的性质
- 6.6 图形的位似
- 6.7用相似三角形解决问题
- 第7章 锐角函数
- 7.1 正切
- 7.2 正弦、余弦
- 7.3 特殊角的三角函数
- 7.4 由三角函数值求锐角
- 7.5 解直角三角形
- 7.6 用锐角三角函数解决问题
- 第8章 统计和概率的简单应用
- 8.1 中学生的视力情况调查
- 8.2 货比三家
- 8.3 统计分析帮你做预测
- 8.4 抽签方法合理吗
- 8.5 概率帮你做估计
- 8.6 收取多少保险费合理
