探索图形人教版数学五年级下册第三单元(共22张PPT)
文档属性
| 名称 | 探索图形人教版数学五年级下册第三单元(共22张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-08 00:00:00 | ||
图片预览





文档简介
(共22张PPT)
义务教育人教版五年级下册
探索图形
新课导入
正方体有几个顶点?几个面?几条棱?
答:正方体有8个顶点,6个面,12条棱。
用同样大的小正方体拼一个大正方体,至少需要多少个这样的小正方体?
答:至少需要8个这样的小正方体。
探究新知
1.用同样大的小正方体拼成如下的正方体,把它的表面涂上红色。
三面涂红色的小正方体有( )个。
两面涂红色的小正方体有( )个。
一面涂红色的小正方体有( )个。
没有涂红色的小正方体有( )个。
8
0
0
0
①
2.用同样大的小正方体拼成如下的正方体,把它的表面涂上红色。
三面涂红色的小正方体有( )个。
两面涂红色的小正方体有( )个。
一面涂红色的小正方体有( )个。
没有涂红色的小正方体有( )个。
8
12
6
1
②
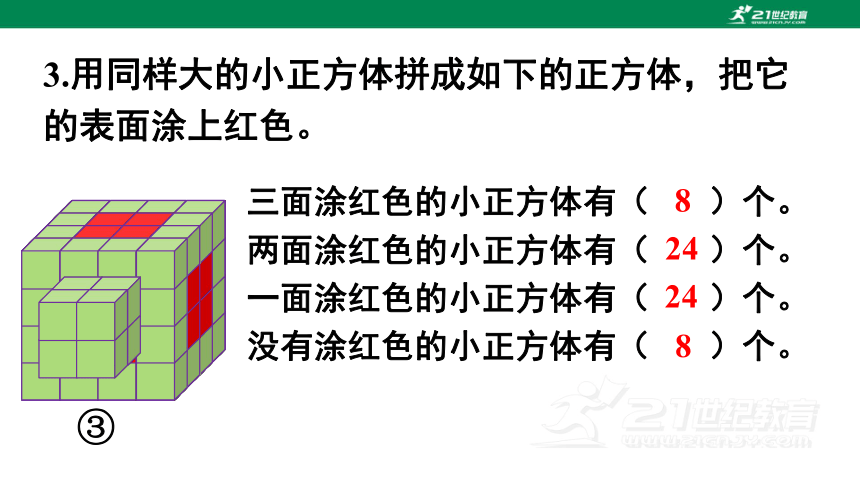
3.用同样大的小正方体拼成如下的正方体,把它的表面涂上红色。
三面涂红色的小正方体有( )个。
两面涂红色的小正方体有( )个。
一面涂红色的小正方体有( )个。
没有涂红色的小正方体有( )个。
8
24
24
8
③
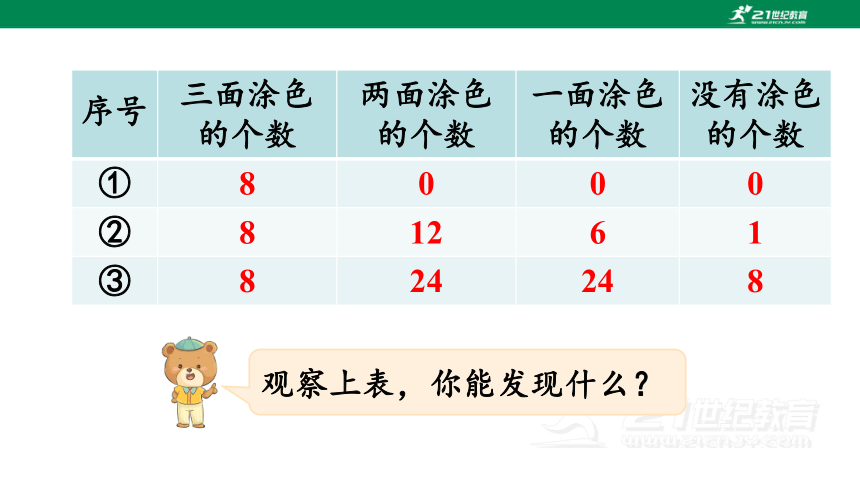
序号 三面涂色的个数 两面涂色的个数 一面涂色的个数 没有涂色的个数
① 8 0 0 0
② 8 12 6 1
③ 8 24 24 8
观察上表,你能发现什么?
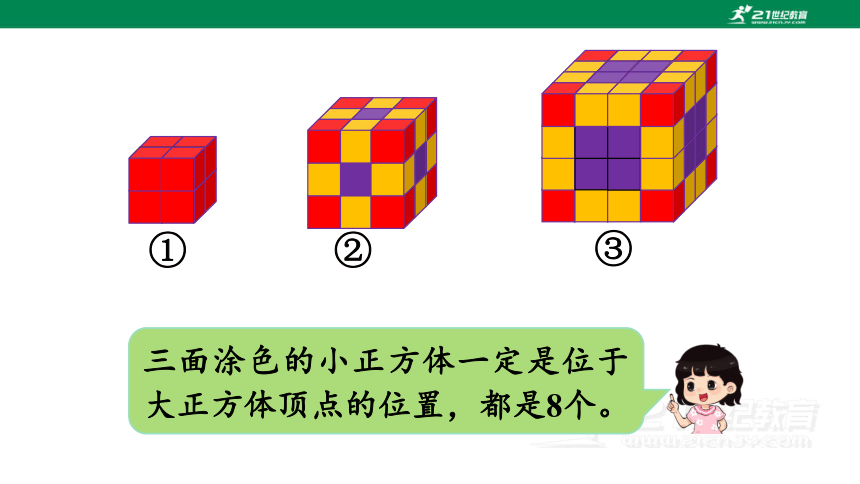
三面涂色的小正方体一定是位于大正方体顶点的位置,都是8个。
①
②
③
①
②
③
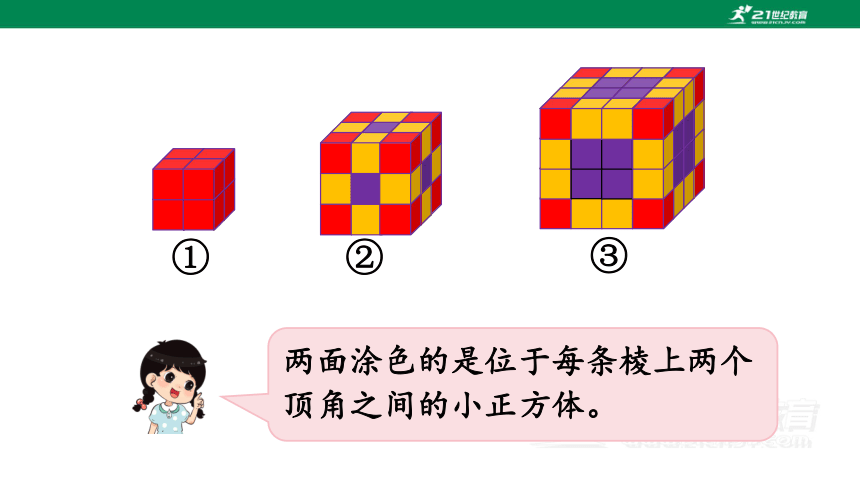
两面涂色的是位于每条棱上两个顶角之间的小正方体。
①
②
③
一面涂色的是每一面上除去外圈的小正方体。
①
②
③
没有涂色的就是隐藏在里面的小正方体。
按这样的规律拼下去,第④、⑤个正方体的结果会是怎样呢?
④
三面涂色:8个
两面涂色:(5-2)×12=36(个)
一面涂色:(5-2) ×6=54(个)
没有涂色:(5-2) =27(个)
⑤
三面涂色:8个
两面涂色:(6-2)×12=48(个)
一面涂色:(6-2) ×6=96(个)
没有涂色:(6-2) =64(个)
根据刚才的结果把下表补充完整。
序号 三面涂色的个数 两面涂色的个数 一面涂色的个数 没有涂色的个数
① 8 0 0 0
② 8 12 6 1
③ 8 24 24 8
④
⑤
8
36
54
27
8
48
96
64
两面涂色的小正方体为(n-2)×12个;
一面涂色的小正方体为(n-2) ×6个;
总结归纳
所有大正方体(由n3个小正方体拼成的)中:
三面涂色的小正方体都是8个;
没有涂色的小正方体为(n-2) 个。
你能继续写出第⑥、⑦、⑧个正方体中四类小正方体的块数吗?
序号 三面涂色的个数 两面涂色的个数 一面涂色的个数 没有涂色的个数
⑥
⑦
⑧
8 60 150 125
8 72 216 216
8 84 294 343
如果摆成下面的几何体,你会数吗?
第一层:1个
第二层:(1+2)个
第三层:(1+2+3)个
第四层:(1+2+3+4)个
……
第1个图形中的小正方体:1+(1+2)=4(块)
第2个图形中的小正方体:
1+(1+2)+(1+2+3)=10(块)
第3个图形中的小正方体:
1+(1+2)+(1+2+3)+(1+2+3+4)=20(块)
巩固运用
把一个1dm3的正方体木块的表面涂上红色,再锯成棱长为1cm的小正方体。
(1)三面涂色的小正方体有多少个?
答:三面涂色的小正方体有8个。
把一个1dm3的正方体木块的表面涂上红色,再锯成棱长为1cm的小正方体。
(2)两面涂色的小正方体有多少个?
(10 -2) ×12 =96(个)
答:两面涂色的小正方体有96个。
把一个1dm3的正方体木块的表面涂上红色,再锯成棱长为1cm的小正方体。
(3)一面涂色的小正方体有多少个?
(10 -2)2 ×6 =384(个)
答:一面涂色的小正方体有384个。
把一个1dm3的正方体木块的表面涂上红色,再锯成棱长为1cm的小正方体。
(4)没有涂色的小正方体有多少个?
(10 -2)3 =512(个)
答:没有涂色的小正方体有512个。
义务教育人教版五年级下册
探索图形
新课导入
正方体有几个顶点?几个面?几条棱?
答:正方体有8个顶点,6个面,12条棱。
用同样大的小正方体拼一个大正方体,至少需要多少个这样的小正方体?
答:至少需要8个这样的小正方体。
探究新知
1.用同样大的小正方体拼成如下的正方体,把它的表面涂上红色。
三面涂红色的小正方体有( )个。
两面涂红色的小正方体有( )个。
一面涂红色的小正方体有( )个。
没有涂红色的小正方体有( )个。
8
0
0
0
①
2.用同样大的小正方体拼成如下的正方体,把它的表面涂上红色。
三面涂红色的小正方体有( )个。
两面涂红色的小正方体有( )个。
一面涂红色的小正方体有( )个。
没有涂红色的小正方体有( )个。
8
12
6
1
②
3.用同样大的小正方体拼成如下的正方体,把它的表面涂上红色。
三面涂红色的小正方体有( )个。
两面涂红色的小正方体有( )个。
一面涂红色的小正方体有( )个。
没有涂红色的小正方体有( )个。
8
24
24
8
③
序号 三面涂色的个数 两面涂色的个数 一面涂色的个数 没有涂色的个数
① 8 0 0 0
② 8 12 6 1
③ 8 24 24 8
观察上表,你能发现什么?
三面涂色的小正方体一定是位于大正方体顶点的位置,都是8个。
①
②
③
①
②
③
两面涂色的是位于每条棱上两个顶角之间的小正方体。
①
②
③
一面涂色的是每一面上除去外圈的小正方体。
①
②
③
没有涂色的就是隐藏在里面的小正方体。
按这样的规律拼下去,第④、⑤个正方体的结果会是怎样呢?
④
三面涂色:8个
两面涂色:(5-2)×12=36(个)
一面涂色:(5-2) ×6=54(个)
没有涂色:(5-2) =27(个)
⑤
三面涂色:8个
两面涂色:(6-2)×12=48(个)
一面涂色:(6-2) ×6=96(个)
没有涂色:(6-2) =64(个)
根据刚才的结果把下表补充完整。
序号 三面涂色的个数 两面涂色的个数 一面涂色的个数 没有涂色的个数
① 8 0 0 0
② 8 12 6 1
③ 8 24 24 8
④
⑤
8
36
54
27
8
48
96
64
两面涂色的小正方体为(n-2)×12个;
一面涂色的小正方体为(n-2) ×6个;
总结归纳
所有大正方体(由n3个小正方体拼成的)中:
三面涂色的小正方体都是8个;
没有涂色的小正方体为(n-2) 个。
你能继续写出第⑥、⑦、⑧个正方体中四类小正方体的块数吗?
序号 三面涂色的个数 两面涂色的个数 一面涂色的个数 没有涂色的个数
⑥
⑦
⑧
8 60 150 125
8 72 216 216
8 84 294 343
如果摆成下面的几何体,你会数吗?
第一层:1个
第二层:(1+2)个
第三层:(1+2+3)个
第四层:(1+2+3+4)个
……
第1个图形中的小正方体:1+(1+2)=4(块)
第2个图形中的小正方体:
1+(1+2)+(1+2+3)=10(块)
第3个图形中的小正方体:
1+(1+2)+(1+2+3)+(1+2+3+4)=20(块)
巩固运用
把一个1dm3的正方体木块的表面涂上红色,再锯成棱长为1cm的小正方体。
(1)三面涂色的小正方体有多少个?
答:三面涂色的小正方体有8个。
把一个1dm3的正方体木块的表面涂上红色,再锯成棱长为1cm的小正方体。
(2)两面涂色的小正方体有多少个?
(10 -2) ×12 =96(个)
答:两面涂色的小正方体有96个。
把一个1dm3的正方体木块的表面涂上红色,再锯成棱长为1cm的小正方体。
(3)一面涂色的小正方体有多少个?
(10 -2)2 ×6 =384(个)
答:一面涂色的小正方体有384个。
把一个1dm3的正方体木块的表面涂上红色,再锯成棱长为1cm的小正方体。
(4)没有涂色的小正方体有多少个?
(10 -2)3 =512(个)
答:没有涂色的小正方体有512个。
