28.2.1 解直角三角形跟踪练(含解析)2022-2023学年人教版数学九年级下册
文档属性
| 名称 | 28.2.1 解直角三角形跟踪练(含解析)2022-2023学年人教版数学九年级下册 |

|
|
| 格式 | docx | ||
| 文件大小 | 570.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-08 15:36:19 | ||
图片预览



文档简介
28.2.1 解直角三角形
一、单选题
1.在中,,则的值( ).
A.大于1 B.等于1 C.小于1 D.不能确定
2.在Rt△ABC中,∠C=90°,∠B=35°,AB=3,则BC的长为( )
A.3sin35° B.2cos35° C.3cos35° D.3tan35°
3.如图,在矩形ABCD中,AD=10,将矩形ABCD绕点A逆时针旋转至BC恰好经过点D,得到矩形AB′C′D′,此时旋转角为θ,若tanθ=,则cos∠ADD'为( )
A. B. C. D.
4.如图,,,AC=10,则的面积是( )
A.42 B.43 C.44 D.45
5.在△ABC中,∠C=90°,AC=3,AB=4,欲求∠A的值,最适宜的做法是( )
A.计算tanA的值求出 B.计算sinA的值求出
C.计算cosA的值求出 D.先根据sinB求出∠B,再利用90°-∠B求出
6.已知:如图,在△ABC中,∠A=45°,sinB=,AC=,那么AB的长度是( )
A.1+2 B.1+ C.3 D.9
7.如图,校园内有两棵树,相距8米,一棵树树高13米,另一棵树高7米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞( )
A.8米 B.9米 C.10米 D.11米
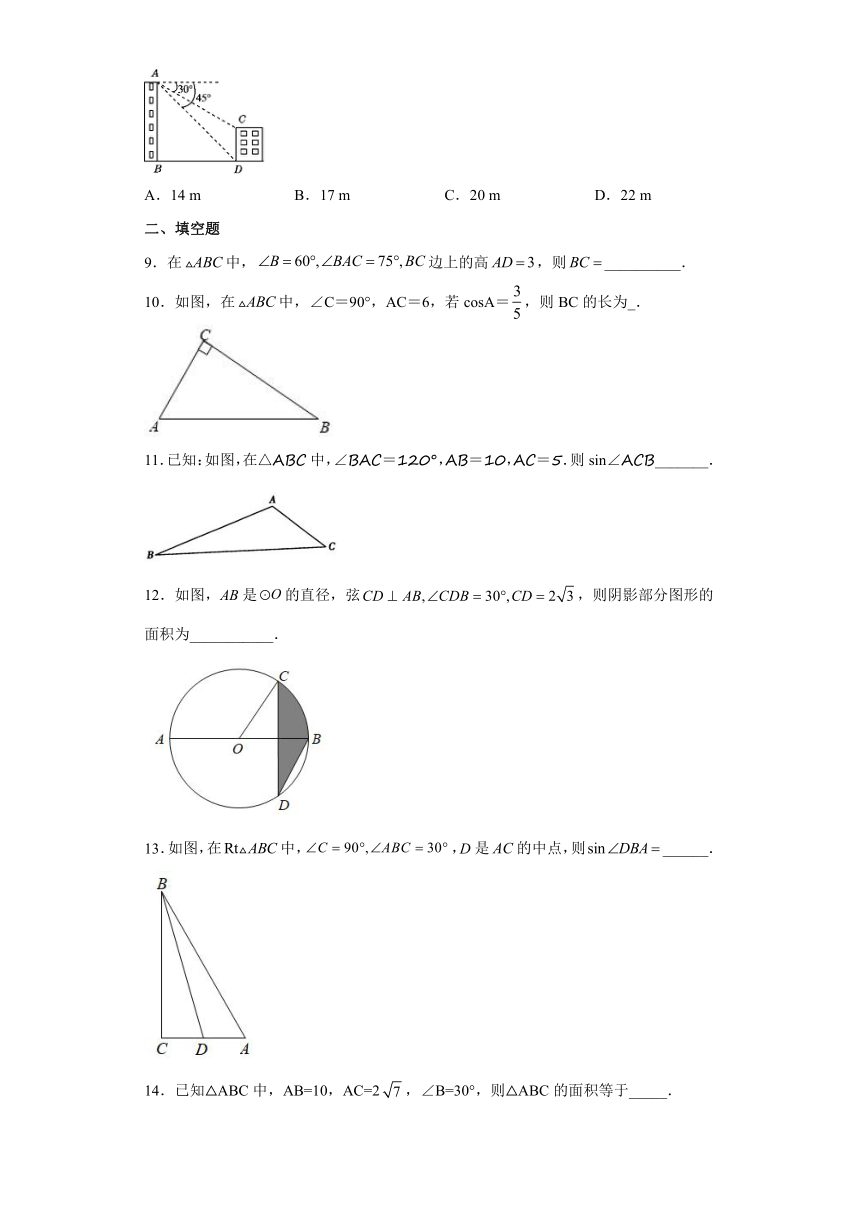
8.如图,两建筑物的水平距离为32 m,从点A测得点C的俯角为30°,点D的俯角为45°,则建筑物CD的高约为( )
A.14 m B.17 m C.20 m D.22 m
二、填空题
9.在中,边上的高,则__________.
10.如图,在中,∠C=90°,AC=6,若cosA=,则BC的长为_.
11.已知:如图,在△ABC中,∠BAC=120°,AB=10,AC=5.则sin∠ACB_______.
12.如图,AB是的直径,弦,则阴影部分图形的面积为___________.
13.如图,在中,,D是的中点,则______.
14.已知△ABC中,AB=10,AC=2,∠B=30°,则△ABC的面积等于_____.
15.如图,的半径于点,.则________.
三、解答题
16.如图,在Rt中,,求和的值.
17.等腰三角形的底角是,腰长为,求它的周长.
18.在中,,根据下列条件解直角三角形:
(1),;
(2),;
(3),.
19.(1)已知是锐角,,求的其他三角函数值;
(2)已知是锐角,,求的其他三角函数值.
20.如图,中,是中点,过点作直线的垂线,垂足为点.
求的值.
连接求四边形的面积.
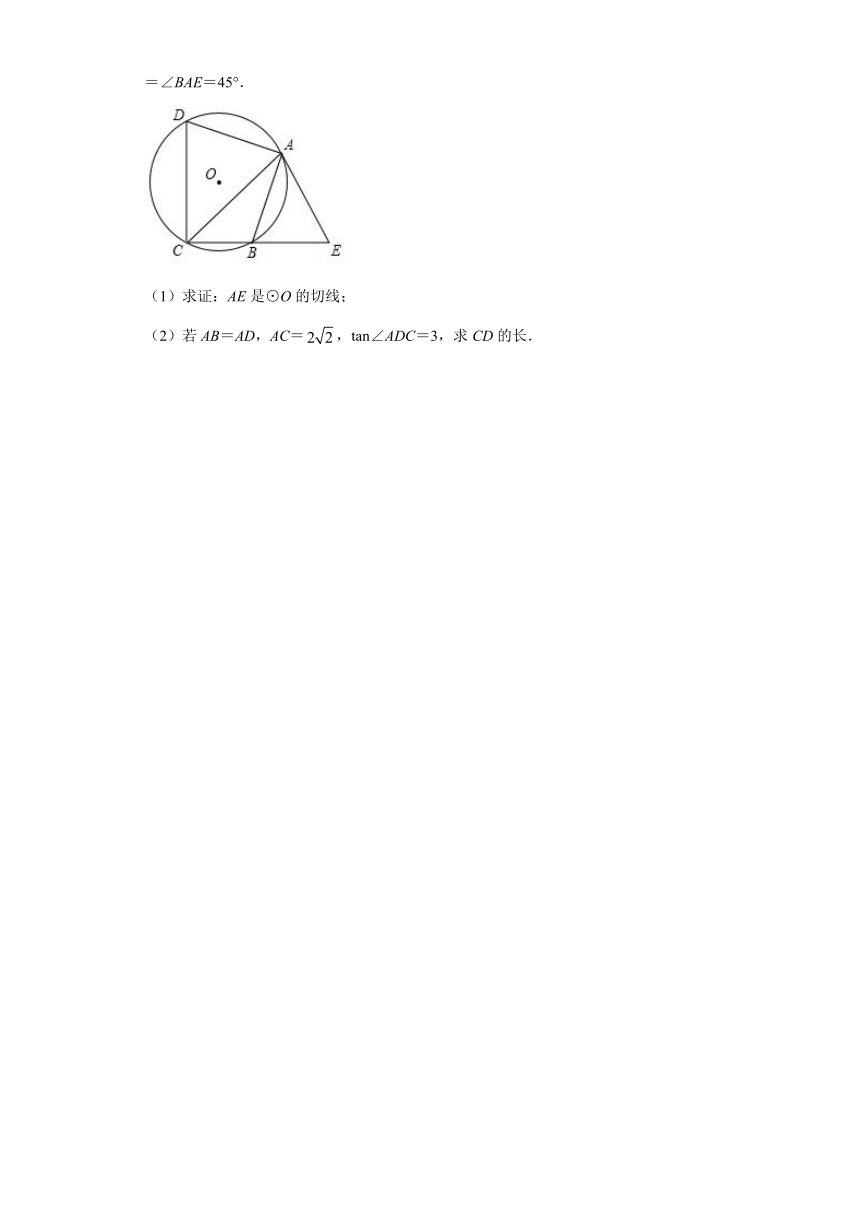
21.如图,四边形ABCD内接于⊙O,点E在CB的延长线上,连接AC,AE,∠ACB=∠BAE=45°.
(1)求证:AE是⊙O的切线;
(2)若AB=AD,AC=,tan∠ADC=3,求CD的长.
参考答案:
1.A
解:设直角三角形ABC中,∠A的对边长为a,∠B的对边长为b,∠C的对边长为c,
∴,,
∴,
由三角形三边的关系得:,
∴,
∴,
2.C
3.C
解:过点作于点,
将矩形绕点逆时针旋转至恰好经过点,
,,
,
,
设,,
在△中,由勾股定理得:,
,
,
,,
,
在中,由勾股定理得:
,
,
4.A
过点A作AD⊥BC于点D,
∵sinC= ,
∴AD=AC sinC=6,
∴由勾股定理可知:BC=8,
∵cosB= ,
∴∠B=45°,
∴BD=AD=6,
∴BC=14,
∴△ABC的面积为BC AD=×6×14=42.
5.C
6.A
过C点作CD⊥AB于D,
∵在△ABC中,CD是AB边上的高,∠A=45°,sinB= ,AC= ,
∴CD=AD=1,
∴BC=3,
∴BD=,
∴AB=AD+BD=1+2.
7.C
如图所示,
AB,CD为树,且AB=13,CD=8,BD为两树距离12米,
过C作CE⊥AB于E,
则CE=BD=8,AE=AB-CD=6,
在直角三角形AEC中,
AC=10米,
答:小鸟至少要飞10米.
8.A
延长DC、交AE与E,
∠EAC=30°,∠EAD=45°,
∴CE=AE=米,DE=AE1=32米,
∴CD=32米 米≈14米,
9.
解:如图,
∵AD⊥BC,
∴,
∵,
∴,
∵,
∴,,
∴.
故答案为.
10.8
解:∵在△ABC中,∠C=90°,AC=6,cosA=,
∴cosA=,
∴AB=10,
∴BC=.
故答案为:8.
11.
解:作BD⊥AC交CA的延长线于D,如图,
∵∠BAC=120°,
∴∠BAD=60°,
在Rt△ABD中,∠ABD=30°,AB=10,
∴AD=AB=5,BD=5,
∴CD=AC+AD=5+5=10,
在Rt△BCD中,BC==5,
∴sin∠ACB===.
12.
解:如图,假设线段、交于点,
是的直径,弦,
,
又,
,,
,,
.
故答案为:.
13.
如图,过点D作于点E,
∵在中,
∴,设,则,,又∵D是边的中点,
∴,
在中,,
在中,,
在中,.
14.15或10
解:作AD⊥BC交BC(或BC延长线)于点D,
①如图1,当AB、AC位于AD异侧时,
在Rt△ABD中,∵∠B=30°,AB=10,
∴AD=ABsinB=5,BD=ABcosB=5,
在Rt△ACD中,∵AC=2,
∴CD=,
则BC=BD+CD=6,
∴S△ABC= BC AD=×6×5=15;
②如图2,当AB、AC在AD的同侧时,
由①知,BD=5,CD=,
则BC=BD-CD=4,
∴S△ABC= BC AD=×4×5=10.
综上,△ABC的面积是15或10,
故答案为15或10.
15.24
16.图(1)中,;图(2)中,
解:(1)在中,,
∴,
∴,
.
(2)在中,,
∴,
∴,
.
17..
解:如图,中,,
过点作于点,
,
,
,
,
的周长为.
18.(1),,;(2),,;(3),,.
解:(1)由勾股定理得,a==10,
∵sinB=,
∴∠B≈42°,
∴∠A=90°-42°=48°,
(2)∵∠B=72°,
∴∠A=90°-∠B=18°,
∵sinA==0.309,sinB==0.951,
∴,;
(3)∵∠B=30°,
∴∠A=60°,
∴sinA=,
∴c=,
由勾股定理得b=.
19.(1),;(2),.
设,为锐角,,,分别都是、、的对应边
(1),
,即,
由勾股定理得:,
,
;
(2),
,即,
由勾股定理得:,
,
.
20.(1);(2)
在中,
而,,
是中点,
;
在中,,
,
是中点,
,
即,
在中, ;
在中,,
是中点,
,
21.(1)见解析(2)
(1)证明:连接OA、OB,如图1所示:
∵∠ACB=45°,
∴∠AOB=2∠ACB=90°,
∵OA=OB,
∴∠OAB=∠OBA=45°,
∵∠BAE=45°,
∴∠OAE=∠OAB+∠BAE=90°,
∴AE⊥OA,
∴AE是⊙O的切线;
(2)解:作AF⊥CD于F,如图2所示:
∵AB=AD,
∴,
∴∠ACB=∠ACD=45°,
∵AF⊥CD,
∴∠AFC=∠AFD=90°,
∵AC=2,
∴在Rt△AFC中,AF=CF=AC sin∠ACF=2×=2,
∵在Rt△AFD中,tan∠ADC==3,
∴DF=,
∴CD=CF+DF=2+=.
一、单选题
1.在中,,则的值( ).
A.大于1 B.等于1 C.小于1 D.不能确定
2.在Rt△ABC中,∠C=90°,∠B=35°,AB=3,则BC的长为( )
A.3sin35° B.2cos35° C.3cos35° D.3tan35°
3.如图,在矩形ABCD中,AD=10,将矩形ABCD绕点A逆时针旋转至BC恰好经过点D,得到矩形AB′C′D′,此时旋转角为θ,若tanθ=,则cos∠ADD'为( )
A. B. C. D.
4.如图,,,AC=10,则的面积是( )
A.42 B.43 C.44 D.45
5.在△ABC中,∠C=90°,AC=3,AB=4,欲求∠A的值,最适宜的做法是( )
A.计算tanA的值求出 B.计算sinA的值求出
C.计算cosA的值求出 D.先根据sinB求出∠B,再利用90°-∠B求出
6.已知:如图,在△ABC中,∠A=45°,sinB=,AC=,那么AB的长度是( )
A.1+2 B.1+ C.3 D.9
7.如图,校园内有两棵树,相距8米,一棵树树高13米,另一棵树高7米,一只小鸟从一棵树的顶端飞到另一棵树的顶端,小鸟至少要飞( )
A.8米 B.9米 C.10米 D.11米
8.如图,两建筑物的水平距离为32 m,从点A测得点C的俯角为30°,点D的俯角为45°,则建筑物CD的高约为( )
A.14 m B.17 m C.20 m D.22 m
二、填空题
9.在中,边上的高,则__________.
10.如图,在中,∠C=90°,AC=6,若cosA=,则BC的长为_.
11.已知:如图,在△ABC中,∠BAC=120°,AB=10,AC=5.则sin∠ACB_______.
12.如图,AB是的直径,弦,则阴影部分图形的面积为___________.
13.如图,在中,,D是的中点,则______.
14.已知△ABC中,AB=10,AC=2,∠B=30°,则△ABC的面积等于_____.
15.如图,的半径于点,.则________.
三、解答题
16.如图,在Rt中,,求和的值.
17.等腰三角形的底角是,腰长为,求它的周长.
18.在中,,根据下列条件解直角三角形:
(1),;
(2),;
(3),.
19.(1)已知是锐角,,求的其他三角函数值;
(2)已知是锐角,,求的其他三角函数值.
20.如图,中,是中点,过点作直线的垂线,垂足为点.
求的值.
连接求四边形的面积.
21.如图,四边形ABCD内接于⊙O,点E在CB的延长线上,连接AC,AE,∠ACB=∠BAE=45°.
(1)求证:AE是⊙O的切线;
(2)若AB=AD,AC=,tan∠ADC=3,求CD的长.
参考答案:
1.A
解:设直角三角形ABC中,∠A的对边长为a,∠B的对边长为b,∠C的对边长为c,
∴,,
∴,
由三角形三边的关系得:,
∴,
∴,
2.C
3.C
解:过点作于点,
将矩形绕点逆时针旋转至恰好经过点,
,,
,
,
设,,
在△中,由勾股定理得:,
,
,
,,
,
在中,由勾股定理得:
,
,
4.A
过点A作AD⊥BC于点D,
∵sinC= ,
∴AD=AC sinC=6,
∴由勾股定理可知:BC=8,
∵cosB= ,
∴∠B=45°,
∴BD=AD=6,
∴BC=14,
∴△ABC的面积为BC AD=×6×14=42.
5.C
6.A
过C点作CD⊥AB于D,
∵在△ABC中,CD是AB边上的高,∠A=45°,sinB= ,AC= ,
∴CD=AD=1,
∴BC=3,
∴BD=,
∴AB=AD+BD=1+2.
7.C
如图所示,
AB,CD为树,且AB=13,CD=8,BD为两树距离12米,
过C作CE⊥AB于E,
则CE=BD=8,AE=AB-CD=6,
在直角三角形AEC中,
AC=10米,
答:小鸟至少要飞10米.
8.A
延长DC、交AE与E,
∠EAC=30°,∠EAD=45°,
∴CE=AE=米,DE=AE1=32米,
∴CD=32米 米≈14米,
9.
解:如图,
∵AD⊥BC,
∴,
∵,
∴,
∵,
∴,,
∴.
故答案为.
10.8
解:∵在△ABC中,∠C=90°,AC=6,cosA=,
∴cosA=,
∴AB=10,
∴BC=.
故答案为:8.
11.
解:作BD⊥AC交CA的延长线于D,如图,
∵∠BAC=120°,
∴∠BAD=60°,
在Rt△ABD中,∠ABD=30°,AB=10,
∴AD=AB=5,BD=5,
∴CD=AC+AD=5+5=10,
在Rt△BCD中,BC==5,
∴sin∠ACB===.
12.
解:如图,假设线段、交于点,
是的直径,弦,
,
又,
,,
,,
.
故答案为:.
13.
如图,过点D作于点E,
∵在中,
∴,设,则,,又∵D是边的中点,
∴,
在中,,
在中,,
在中,.
14.15或10
解:作AD⊥BC交BC(或BC延长线)于点D,
①如图1,当AB、AC位于AD异侧时,
在Rt△ABD中,∵∠B=30°,AB=10,
∴AD=ABsinB=5,BD=ABcosB=5,
在Rt△ACD中,∵AC=2,
∴CD=,
则BC=BD+CD=6,
∴S△ABC= BC AD=×6×5=15;
②如图2,当AB、AC在AD的同侧时,
由①知,BD=5,CD=,
则BC=BD-CD=4,
∴S△ABC= BC AD=×4×5=10.
综上,△ABC的面积是15或10,
故答案为15或10.
15.24
16.图(1)中,;图(2)中,
解:(1)在中,,
∴,
∴,
.
(2)在中,,
∴,
∴,
.
17..
解:如图,中,,
过点作于点,
,
,
,
,
的周长为.
18.(1),,;(2),,;(3),,.
解:(1)由勾股定理得,a==10,
∵sinB=,
∴∠B≈42°,
∴∠A=90°-42°=48°,
(2)∵∠B=72°,
∴∠A=90°-∠B=18°,
∵sinA==0.309,sinB==0.951,
∴,;
(3)∵∠B=30°,
∴∠A=60°,
∴sinA=,
∴c=,
由勾股定理得b=.
19.(1),;(2),.
设,为锐角,,,分别都是、、的对应边
(1),
,即,
由勾股定理得:,
,
;
(2),
,即,
由勾股定理得:,
,
.
20.(1);(2)
在中,
而,,
是中点,
;
在中,,
,
是中点,
,
即,
在中, ;
在中,,
是中点,
,
21.(1)见解析(2)
(1)证明:连接OA、OB,如图1所示:
∵∠ACB=45°,
∴∠AOB=2∠ACB=90°,
∵OA=OB,
∴∠OAB=∠OBA=45°,
∵∠BAE=45°,
∴∠OAE=∠OAB+∠BAE=90°,
∴AE⊥OA,
∴AE是⊙O的切线;
(2)解:作AF⊥CD于F,如图2所示:
∵AB=AD,
∴,
∴∠ACB=∠ACD=45°,
∵AF⊥CD,
∴∠AFC=∠AFD=90°,
∵AC=2,
∴在Rt△AFC中,AF=CF=AC sin∠ACF=2×=2,
∵在Rt△AFD中,tan∠ADC==3,
∴DF=,
∴CD=CF+DF=2+=.
