18.2.2菱形的判定 课件 (共32张PPT)
文档属性
| 名称 | 18.2.2菱形的判定 课件 (共32张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-07 21:59:58 | ||
图片预览







文档简介
(共32张PPT)
18.2.2 菱形的判定
人教版八年级下册
知识回顾
四条边都相等
两条对角线互相垂直,并且每一条对角线平分一组对角.
轴对称图形,有两条对称轴.
菱形的特殊性质有哪些?
1.掌握菱形的判定及证明过程.
2.能熟练运用菱形的判定进行计算和证明.
教学目标
新知导入
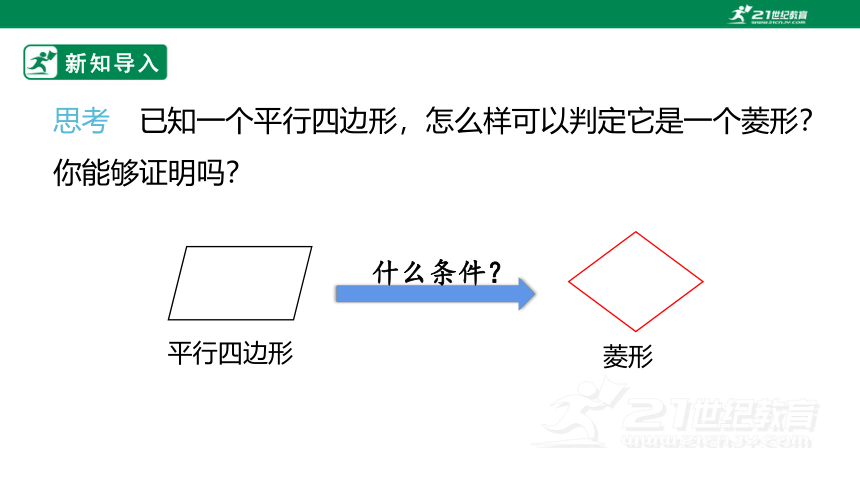
思考 已知一个平行四边形,怎么样可以判定它是一个菱形?你能够证明吗?
平行四边形
什么条件?
菱形
新知探究
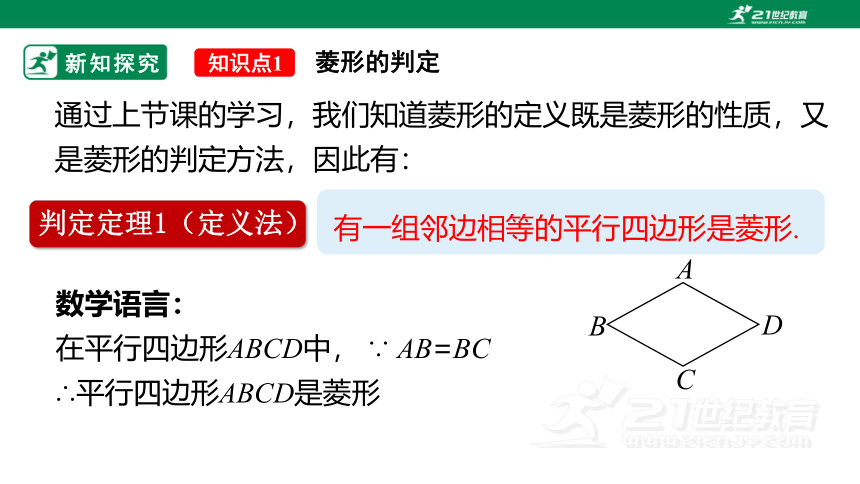
有一组邻边相等的平行四边形是菱形.
数学语言:
在平行四边形ABCD中, ∵ AB=BC
∴平行四边形ABCD是菱形
A
B
D
C
通过上节课的学习,我们知道菱形的定义既是菱形的性质,又是菱形的判定方法,因此有:
知识点1
菱形的判定
判定定理1(定义法)
新知典例
证明:
∵DE∥AC,CE∥BD,
例1.如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD.
求证:四边形OCED是菱形.
∴四边形OCED是平行四边形.
( )
∵四边形ABCD是矩形,
∴OC=OD,( )
∴四边形OCED是菱形.
( )
两组对边分别平行的四边形是平行四边形
矩形的对角线相等且互相平分
有一组邻边相等的平行四边形是菱形
新知练习
证明:
1.如图,在△ABC中,AD⊥BC于D,点D、E、F分别是BC、AB、AC的中点.
求证:四边形AEDF是菱形.
∵点D、E、F分别是BC、AB、AC的中点,
∴DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形.
又∵AD⊥BC,BD=CD,
∴AB=AC,
∴AE=AF,
∴平行四边形AEDF是菱形.
新知探究
与研究平行四边形和矩形的判定方法类似,我们研究菱形的性质定理的逆命题,看看它们是否成立.
前提条件是平行四边形
对角线互相垂直的平行四边形是菱形.
菱形的对角线互相垂直.
题设
结论
新知探究
你能试着给出证明吗?
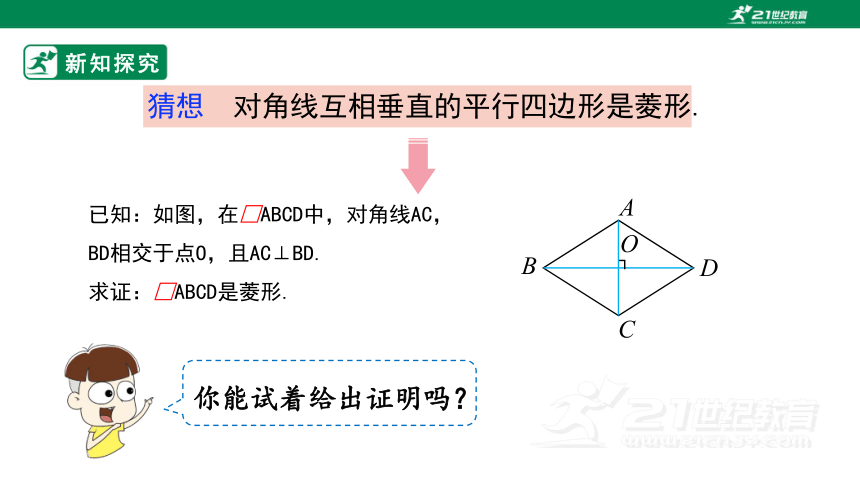
A
B
D
C
O
┐
猜想 对角线互相垂直的平行四边形是菱形.
已知:如图,在□ABCD中,对角线AC,
BD相交于点O,且AC⊥BD.
求证:□ABCD是菱形.
新知探究
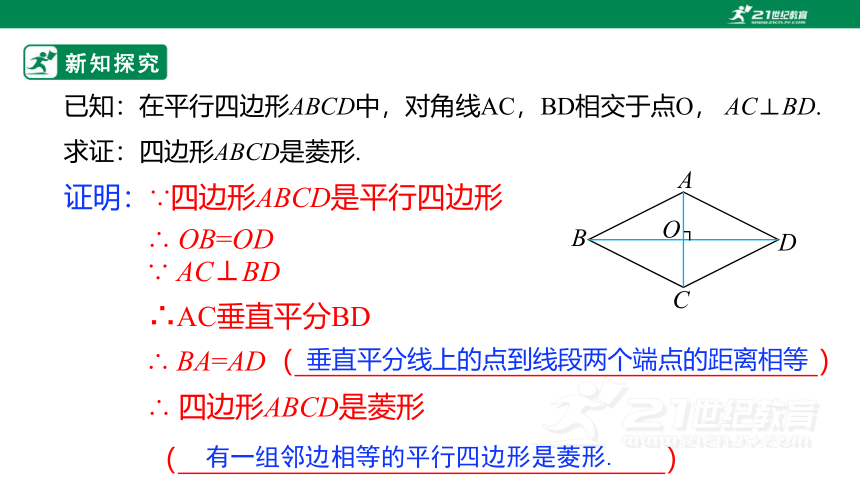
已知:在平行四边形ABCD中,对角线AC,BD相交于点O, AC⊥BD.
求证:四边形ABCD是菱形.
证明:∵四边形ABCD是平行四边形
∴ OB=OD
∵ AC⊥BD
∴AC垂直平分BD
∴ BA=AD( )
∴ 四边形ABCD是菱形( )
A
B
D
C
O
┐
垂直平分线上的点到线段两个端点的距离相等
有一组邻边相等的平行四边形是菱形.
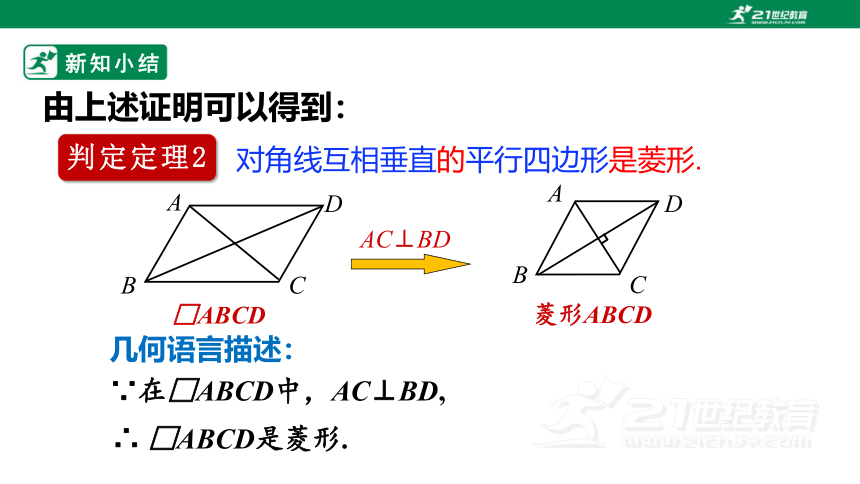
新知小结
判定定理2
由上述证明可以得到:
对角线互相垂直的平行四边形是菱形.
几何语言描述:
∴ □ABCD是菱形.
∵在□ABCD中,AC⊥BD,
AC⊥BD
A
B
C
D
菱形ABCD
A
B
C
D
□ABCD
新知探究
例2 如图,平行四边形ABCD的对角线AC、BD相交于点O,且AB=5,AO=4,BO=3. 求证:平行四边形ABCD是菱形.
D
A
C
B
O
证明:∵ AB=5,AO=4,BO=3
∴+
∴△AOB是直角三角形( )
∴AC⊥BD
∴ 平行四边形ABCD是菱形
( )
勾股定理逆定理
对角线互相垂直的平行四边形是菱形
新知探究
2.已知:如图,?ABCD的对角线AC垂直平分线与边AD、BC分别交于E、F.
求证:四边形AFCE是菱形.
证明:
∵四边形ABCD是平行四边形,
∴AE∥FC. ∴∠1=∠2,
又∠AOE=∠COF,AO=CO,
∴△AOE≌△COF(ASA)
∴EO=FO.
∴四边形AFCE是平行四边形.
又∵EF⊥AC,
∴
AFCE是菱形.
新知探究
思考 动手画出一个四边形,满足有两条边相等的四边形是菱形吗?
不是
不是
?
你能进行证明吗?
三条边相等呢?
四条边相等呢?
新知探究
已知:在四边形ABCD中,AB=BC=CD=DA. 求证:四边形ABCD是菱形.
证明:∵ AB=CD=BC=DA
∴四边形ABCD是平行四边形
∵ AB=BC
∴四边形ABCD是菱形
A
B
D
C
新知小结
判定定理3
由上述证明可以得到:
四条边相等的四边形是菱形.
AB=BC=CD=AD
A
B
C
D
菱形ABCD
四边形ABCD
A
B
C
D
几何语言描述:
∴四边形 ABCD是菱形.
∵在四边形ABCD中,AB=BC=CD=AD,
新知典例
证明: ∵ ∠1= ∠2,
又∵AE=AC,AD=AD,
∴ △ACD≌ △AED (SAS).
同理△ACF≌△AEF(SAS) .
∴CD=ED, CF=EF.
又∵EF=ED,∴CD=ED=CF=EF,
∴四边形CDEF是菱形.
2
例3 如图,在△ABC中, AD是角平分线,点E、F分别在AB、 AD上,且AE=AC,EF = ED.
求证:四边形CDEF是菱形.
A
C
B
E
D
F
1
新知练习
B
B
新知练习
3. 如图,在△ABC中,∠B=90°,AB=6cm,BC=8cm.将△ABC沿射线BC方向平移10cm,得到△DEF,A,B,C的对应点分别是D,E,F,连接AD.求证:四边形ACFD是菱形.
证明:由平移变换的性质得CF=AD=10cm,DF=AC.
∵∠B=90°,AB=6cm,BC=8cm,
∴AC=DF=AD=CF=10cm,
∴四边形ACFD是菱形.
四边形的条件中存在多个关于边的等量关系时,运用四条边都相等来判定一个四边形是菱形比较方便.
归纳
新知探究
H
G
F
E
D
C
B
A
证明:连接AC、BD.
∵四边形ABCD是矩形,
∴AC=BD.
∵点E、F、G、H为各边中点,
∴EF=FG=GH=HE,
∴四边形EFGH是菱形.
例4 如图,顺次连接矩形ABCD各边中点,得到四边形EFGH,求证:四边形EFGH是菱形.
新知练习
C
A
B
D
E
F
G
H
4. 如图,顺次连接对角线相等的四边形ABCD各边中点,得到四边形EFGH是什么四边形?
解:四边形EFGH是菱形.
又∵AC=BD,
∵点E、F、G、H为各边中点,
∴EF=FG=GH=HE,
∴四边形EFGH是菱形.
顺次连接对角线相等的四边形的各边中点,得到四边形是菱形.
归纳
理由如下:连接AC、BD
新知探究
知识点2
菱形的性质和判定综合运用
例5 如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
(1)求证:四边形BCFE是菱形;
(1)证明:∵D、E分别是AB、AC的中点,
∴DE∥BC且2DE=BC.
又∵BE=2DE,EF=BE,
∴EF=BC,EF∥BC,
∴四边形BCFE是平行四边形.
又∵EF=BE,
∴四边形BCFE是菱形.
新知探究
(2)解:∵∠BCF=120°,
∴∠EBC=60°,
∴△EBC是等边三角形,
∴菱形的边长为4,高为 ,
∴菱形的面积为 .
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
判定一个四边形是菱形时,要结合条件灵活选择方法.如果可以证明四条边相等,可直接证出菱形;如果只能证出一组邻边相等或对角线互相垂直,可以先尝试证出这个四边形是平行四边形.
归纳
课堂总结
菱形的判定
判定1
判定3
有一组邻边相等的平行四边形是菱形.
判定2
四条边相等的四边形是菱形.
对角线互相垂直的平行四边形是菱形.
课堂练习
1.下列说法中正确的是( ).
C
A.对角线互相垂直的四边形是菱形.
B.两条邻边相等,且一条对角线平分一组对角的四边形是菱形.
C.对角线互相垂直平分的四边形是菱形.
D.两条邻边相等的四边形是菱形.
课堂练习
2.平行四边形ABCD的两对角线AC、BD相交于点O.
(1)若AB=AD,则平行四边形ABCD是 .
(2)若∠BAO=∠DAO,则平行四边形ABCD是 .
(3)若平行四边形ABCD是菱形,则AC BD.
菱形
菱形
⊥
A
B
D
C
O
课堂练习
3.如图,在菱形ABCD中,对角线 AC、BD 交于点O,点 E、F、G、H 分别是 OA、OB、OC、OD 的中点. 求证:四边形EFGH是菱形.
证明: ∵四边形ABCD是菱形
∴ AB=BC=CD=AD
D
A
B
C
O
E
F
G
H
∵点E、F、G、H分别是OA、OB、OC、OD的中点
∴EF、FG、GH、EH是中位线
∴ EF=AB,FG=BC,GH=CD,EH=AD
∴EF=FG=GH=EH
∴四边形EFGH是菱形
课堂练习
4.如图,在平行四边形ABCD中,E、F分别是AD、BC上的点,且DE=BF,AC⊥EF. 求证:四边形AECF是菱形.
证明:∵四边形ABCD是平行四边形
∴ AD=BC, AD//BC
∵ DE=BF
∴ AE=CF, 又AE//CF
∴四边形AECF是平行四边形
A
B
C
D
E
F
∵ AC⊥EF
∴四边形AECF是菱形
课堂练习
4.如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,连接DE、BF、BD.
(1)求证:四边形DEBF为平行四边形;
(1)证明:∵四边形ABCD为平行四边形,
∴AB=CD,AB∥CD,
∵E、F分别为边AB、CD的中点,
∴EB=DF,EB∥DF,
∴四边形DEBF为平行四边形.
A
B
C
D
E
F
课堂练习
4.如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,连接DE、BF、BD.
(2)当∠ADB=90°时,求证:四边形DEBF是菱形.
(2)证明:∵∠ADB=90°,E为边AB的中点,
∴DE= AB=EB,
∵四边形DEBF为平行四边形,
∴四边形DEBF为菱形.
A
B
C
D
E
F
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
18.2.2 菱形的判定
人教版八年级下册
知识回顾
四条边都相等
两条对角线互相垂直,并且每一条对角线平分一组对角.
轴对称图形,有两条对称轴.
菱形的特殊性质有哪些?
1.掌握菱形的判定及证明过程.
2.能熟练运用菱形的判定进行计算和证明.
教学目标
新知导入
思考 已知一个平行四边形,怎么样可以判定它是一个菱形?你能够证明吗?
平行四边形
什么条件?
菱形
新知探究
有一组邻边相等的平行四边形是菱形.
数学语言:
在平行四边形ABCD中, ∵ AB=BC
∴平行四边形ABCD是菱形
A
B
D
C
通过上节课的学习,我们知道菱形的定义既是菱形的性质,又是菱形的判定方法,因此有:
知识点1
菱形的判定
判定定理1(定义法)
新知典例
证明:
∵DE∥AC,CE∥BD,
例1.如图,矩形ABCD的对角线相交于点O,DE∥AC,CE∥BD.
求证:四边形OCED是菱形.
∴四边形OCED是平行四边形.
( )
∵四边形ABCD是矩形,
∴OC=OD,( )
∴四边形OCED是菱形.
( )
两组对边分别平行的四边形是平行四边形
矩形的对角线相等且互相平分
有一组邻边相等的平行四边形是菱形
新知练习
证明:
1.如图,在△ABC中,AD⊥BC于D,点D、E、F分别是BC、AB、AC的中点.
求证:四边形AEDF是菱形.
∵点D、E、F分别是BC、AB、AC的中点,
∴DE∥AC,DF∥AB,
∴四边形AEDF是平行四边形.
又∵AD⊥BC,BD=CD,
∴AB=AC,
∴AE=AF,
∴平行四边形AEDF是菱形.
新知探究
与研究平行四边形和矩形的判定方法类似,我们研究菱形的性质定理的逆命题,看看它们是否成立.
前提条件是平行四边形
对角线互相垂直的平行四边形是菱形.
菱形的对角线互相垂直.
题设
结论
新知探究
你能试着给出证明吗?
A
B
D
C
O
┐
猜想 对角线互相垂直的平行四边形是菱形.
已知:如图,在□ABCD中,对角线AC,
BD相交于点O,且AC⊥BD.
求证:□ABCD是菱形.
新知探究
已知:在平行四边形ABCD中,对角线AC,BD相交于点O, AC⊥BD.
求证:四边形ABCD是菱形.
证明:∵四边形ABCD是平行四边形
∴ OB=OD
∵ AC⊥BD
∴AC垂直平分BD
∴ BA=AD( )
∴ 四边形ABCD是菱形( )
A
B
D
C
O
┐
垂直平分线上的点到线段两个端点的距离相等
有一组邻边相等的平行四边形是菱形.
新知小结
判定定理2
由上述证明可以得到:
对角线互相垂直的平行四边形是菱形.
几何语言描述:
∴ □ABCD是菱形.
∵在□ABCD中,AC⊥BD,
AC⊥BD
A
B
C
D
菱形ABCD
A
B
C
D
□ABCD
新知探究
例2 如图,平行四边形ABCD的对角线AC、BD相交于点O,且AB=5,AO=4,BO=3. 求证:平行四边形ABCD是菱形.
D
A
C
B
O
证明:∵ AB=5,AO=4,BO=3
∴+
∴△AOB是直角三角形( )
∴AC⊥BD
∴ 平行四边形ABCD是菱形
( )
勾股定理逆定理
对角线互相垂直的平行四边形是菱形
新知探究
2.已知:如图,?ABCD的对角线AC垂直平分线与边AD、BC分别交于E、F.
求证:四边形AFCE是菱形.
证明:
∵四边形ABCD是平行四边形,
∴AE∥FC. ∴∠1=∠2,
又∠AOE=∠COF,AO=CO,
∴△AOE≌△COF(ASA)
∴EO=FO.
∴四边形AFCE是平行四边形.
又∵EF⊥AC,
∴
AFCE是菱形.
新知探究
思考 动手画出一个四边形,满足有两条边相等的四边形是菱形吗?
不是
不是
?
你能进行证明吗?
三条边相等呢?
四条边相等呢?
新知探究
已知:在四边形ABCD中,AB=BC=CD=DA. 求证:四边形ABCD是菱形.
证明:∵ AB=CD=BC=DA
∴四边形ABCD是平行四边形
∵ AB=BC
∴四边形ABCD是菱形
A
B
D
C
新知小结
判定定理3
由上述证明可以得到:
四条边相等的四边形是菱形.
AB=BC=CD=AD
A
B
C
D
菱形ABCD
四边形ABCD
A
B
C
D
几何语言描述:
∴四边形 ABCD是菱形.
∵在四边形ABCD中,AB=BC=CD=AD,
新知典例
证明: ∵ ∠1= ∠2,
又∵AE=AC,AD=AD,
∴ △ACD≌ △AED (SAS).
同理△ACF≌△AEF(SAS) .
∴CD=ED, CF=EF.
又∵EF=ED,∴CD=ED=CF=EF,
∴四边形CDEF是菱形.
2
例3 如图,在△ABC中, AD是角平分线,点E、F分别在AB、 AD上,且AE=AC,EF = ED.
求证:四边形CDEF是菱形.
A
C
B
E
D
F
1
新知练习
B
B
新知练习
3. 如图,在△ABC中,∠B=90°,AB=6cm,BC=8cm.将△ABC沿射线BC方向平移10cm,得到△DEF,A,B,C的对应点分别是D,E,F,连接AD.求证:四边形ACFD是菱形.
证明:由平移变换的性质得CF=AD=10cm,DF=AC.
∵∠B=90°,AB=6cm,BC=8cm,
∴AC=DF=AD=CF=10cm,
∴四边形ACFD是菱形.
四边形的条件中存在多个关于边的等量关系时,运用四条边都相等来判定一个四边形是菱形比较方便.
归纳
新知探究
H
G
F
E
D
C
B
A
证明:连接AC、BD.
∵四边形ABCD是矩形,
∴AC=BD.
∵点E、F、G、H为各边中点,
∴EF=FG=GH=HE,
∴四边形EFGH是菱形.
例4 如图,顺次连接矩形ABCD各边中点,得到四边形EFGH,求证:四边形EFGH是菱形.
新知练习
C
A
B
D
E
F
G
H
4. 如图,顺次连接对角线相等的四边形ABCD各边中点,得到四边形EFGH是什么四边形?
解:四边形EFGH是菱形.
又∵AC=BD,
∵点E、F、G、H为各边中点,
∴EF=FG=GH=HE,
∴四边形EFGH是菱形.
顺次连接对角线相等的四边形的各边中点,得到四边形是菱形.
归纳
理由如下:连接AC、BD
新知探究
知识点2
菱形的性质和判定综合运用
例5 如图,在△ABC中,D、E分别是AB、AC的中点,BE=2DE,延长DE到点F,使得EF=BE,连接CF.
(1)求证:四边形BCFE是菱形;
(1)证明:∵D、E分别是AB、AC的中点,
∴DE∥BC且2DE=BC.
又∵BE=2DE,EF=BE,
∴EF=BC,EF∥BC,
∴四边形BCFE是平行四边形.
又∵EF=BE,
∴四边形BCFE是菱形.
新知探究
(2)解:∵∠BCF=120°,
∴∠EBC=60°,
∴△EBC是等边三角形,
∴菱形的边长为4,高为 ,
∴菱形的面积为 .
(2)若CE=4,∠BCF=120°,求菱形BCFE的面积.
判定一个四边形是菱形时,要结合条件灵活选择方法.如果可以证明四条边相等,可直接证出菱形;如果只能证出一组邻边相等或对角线互相垂直,可以先尝试证出这个四边形是平行四边形.
归纳
课堂总结
菱形的判定
判定1
判定3
有一组邻边相等的平行四边形是菱形.
判定2
四条边相等的四边形是菱形.
对角线互相垂直的平行四边形是菱形.
课堂练习
1.下列说法中正确的是( ).
C
A.对角线互相垂直的四边形是菱形.
B.两条邻边相等,且一条对角线平分一组对角的四边形是菱形.
C.对角线互相垂直平分的四边形是菱形.
D.两条邻边相等的四边形是菱形.
课堂练习
2.平行四边形ABCD的两对角线AC、BD相交于点O.
(1)若AB=AD,则平行四边形ABCD是 .
(2)若∠BAO=∠DAO,则平行四边形ABCD是 .
(3)若平行四边形ABCD是菱形,则AC BD.
菱形
菱形
⊥
A
B
D
C
O
课堂练习
3.如图,在菱形ABCD中,对角线 AC、BD 交于点O,点 E、F、G、H 分别是 OA、OB、OC、OD 的中点. 求证:四边形EFGH是菱形.
证明: ∵四边形ABCD是菱形
∴ AB=BC=CD=AD
D
A
B
C
O
E
F
G
H
∵点E、F、G、H分别是OA、OB、OC、OD的中点
∴EF、FG、GH、EH是中位线
∴ EF=AB,FG=BC,GH=CD,EH=AD
∴EF=FG=GH=EH
∴四边形EFGH是菱形
课堂练习
4.如图,在平行四边形ABCD中,E、F分别是AD、BC上的点,且DE=BF,AC⊥EF. 求证:四边形AECF是菱形.
证明:∵四边形ABCD是平行四边形
∴ AD=BC, AD//BC
∵ DE=BF
∴ AE=CF, 又AE//CF
∴四边形AECF是平行四边形
A
B
C
D
E
F
∵ AC⊥EF
∴四边形AECF是菱形
课堂练习
4.如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,连接DE、BF、BD.
(1)求证:四边形DEBF为平行四边形;
(1)证明:∵四边形ABCD为平行四边形,
∴AB=CD,AB∥CD,
∵E、F分别为边AB、CD的中点,
∴EB=DF,EB∥DF,
∴四边形DEBF为平行四边形.
A
B
C
D
E
F
课堂练习
4.如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,连接DE、BF、BD.
(2)当∠ADB=90°时,求证:四边形DEBF是菱形.
(2)证明:∵∠ADB=90°,E为边AB的中点,
∴DE= AB=EB,
∵四边形DEBF为平行四边形,
∴四边形DEBF为菱形.
A
B
C
D
E
F
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
