河北省衡水市阜城第四中学2022-2023学年九年级下学期第一次月考数学试卷(含答案)
文档属性
| 名称 | 河北省衡水市阜城第四中学2022-2023学年九年级下学期第一次月考数学试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 914.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-08 00:00:00 | ||
图片预览

文档简介
中考模拟系列
2023年河北省中考适应性模拟检测
数学试卷(导向一)
(考试时间:120分钟,满分:120分)
一、选择题(本大题共16个小题,1~10小题每题3分;11~16小题每题2分,共42分。在每小题给出的四个选项中,只有一项是符合题目要求的)
1.若则m值为。( )
A. 8 B. 6 C. 5 D. 2
2. 如图1,在△ABC中,D为AC上一点,把△DBC沿BD折叠,使点C落在AC上的点E处,则BD是△ABC的
A. 中线 B. 高线
C. 角平分线 D. 对角线
3.下列各式中的计算结果与相等的是。( )
A. B. C. D.
4.下列各式中正确的是
A. B C. D.
5.一个多边形的内角和为α,外角和为β,则的多边形的是( )
A. B.
C. D.
6. 华为最新款手机芯片“麒麟”是一种微型处理器,每秒可进行100亿次运算,它工作2023秒可进行的运算次数用科学记数法表示为
A. B.
C. D.
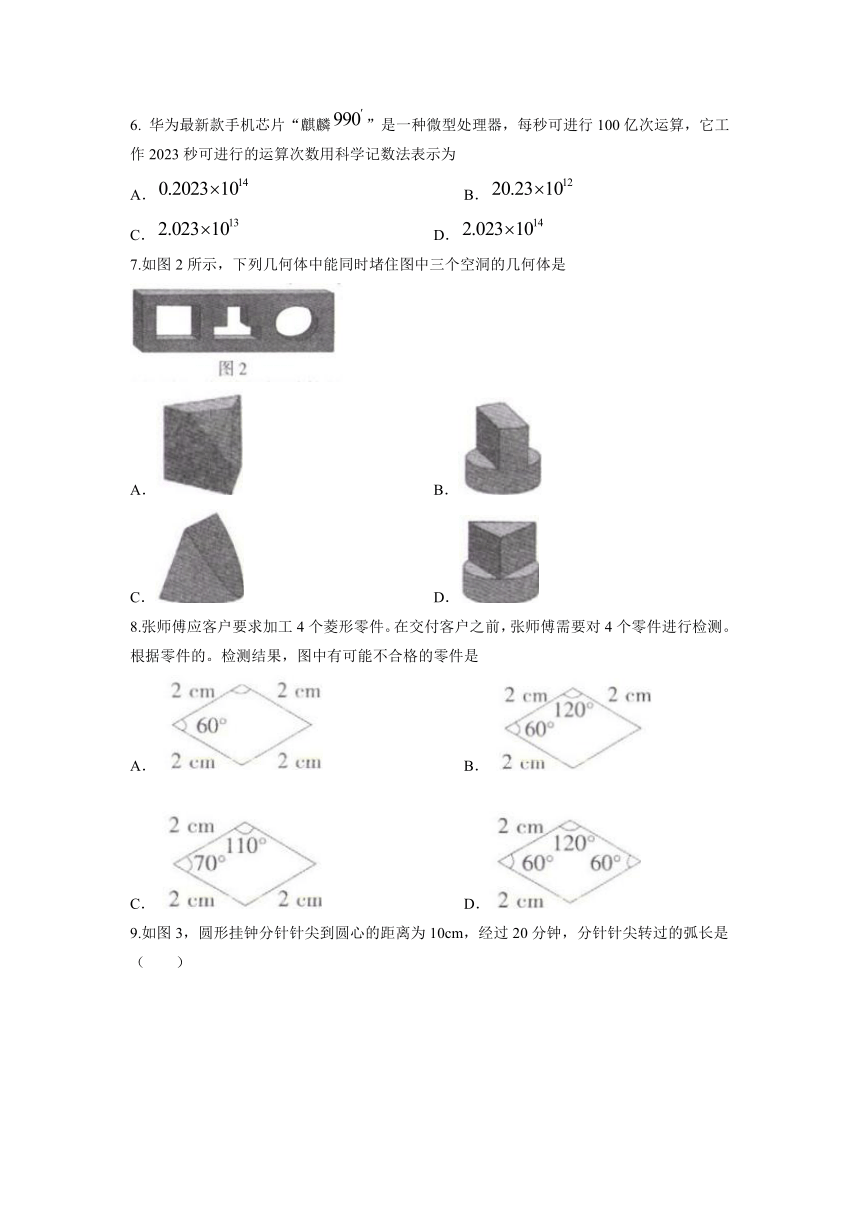
7.如图2所示,下列几何体中能同时堵住图中三个空洞的几何体是
A. B.
C. D.
8.张师傅应客户要求加工4个菱形零件。在交付客户之前,张师傅需要对4个零件进行检测。根据零件的。检测结果,图中有可能不合格的零件是
A. B.
C. D.
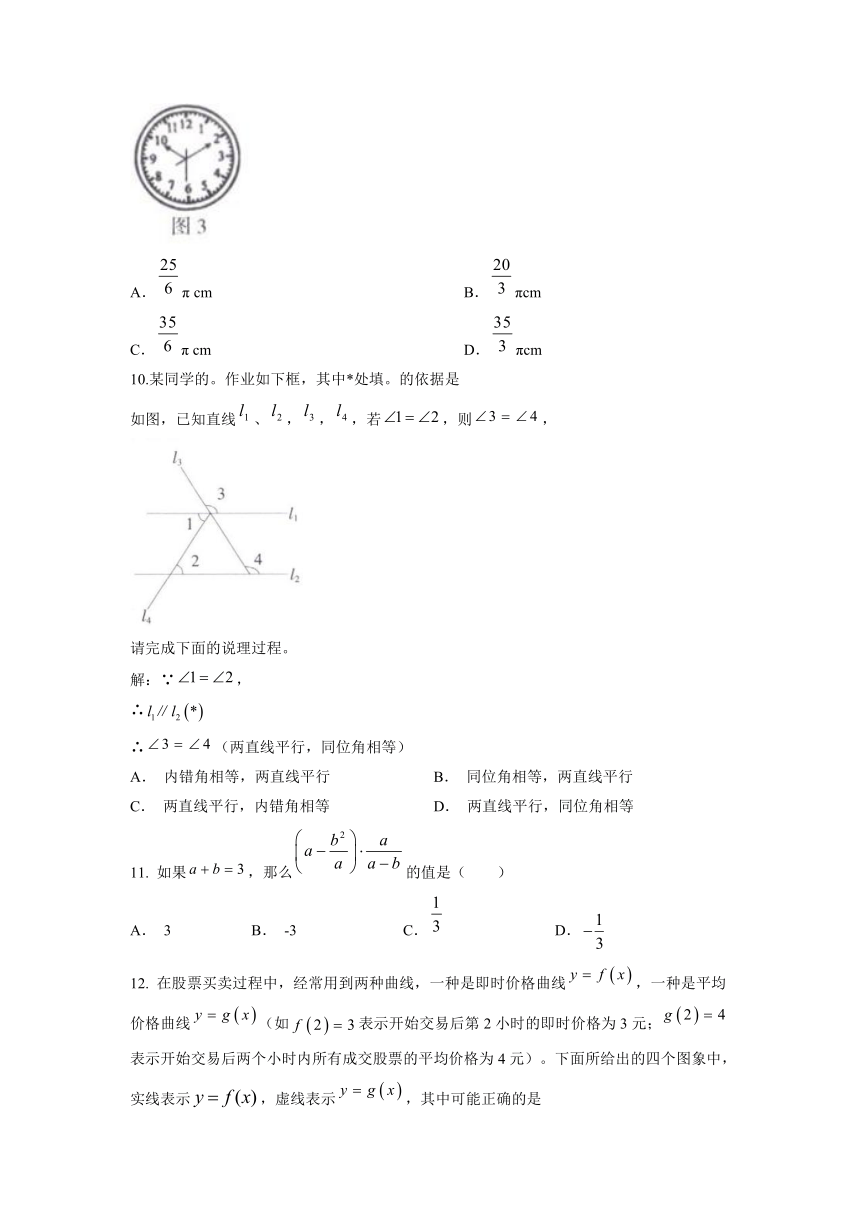
9.如图3,圆形挂钟分针针尖到圆心的距离为10cm,经过20分钟,分针针尖转过的弧长是( )
A.π cm B.πcm
C.π cm D.πcm
10.某同学的。作业如下框,其中*处填。的依据是
如图,已知直线、,,,若,则,
请完成下面的说理过程。
解:∵,
∴
∴(两直线平行,同位角相等)
A. 内错角相等,两直线平行 B. 同位角相等,两直线平行
C. 两直线平行,内错角相等 D. 两直线平行,同位角相等
11. 如果,那么的值是( )
A. 3 B. -3 C. D.
12. 在股票买卖过程中,经常用到两种曲线,一种是即时价格曲线,一种是平均价格曲线(如表示开始交易后第2小时的即时价格为3元;表示开始交易后两个小时内所有成交股票的平均价格为4元)。下面所给出的四个图象中,实线表示,虚线表示,其中可能正确的是
A. B.
C. D.
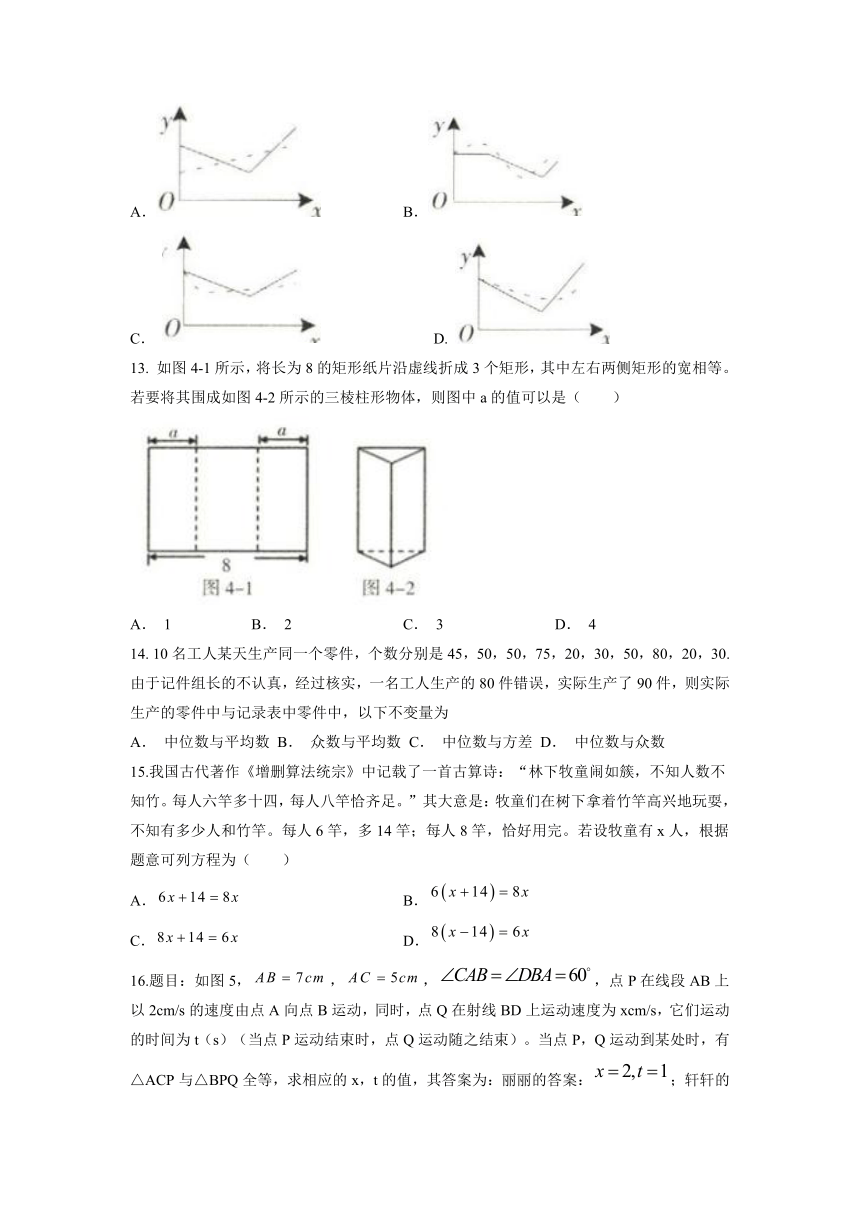
13. 如图4-1所示,将长为8的矩形纸片沿虚线折成3个矩形,其中左右两侧矩形的宽相等。若要将其围成如图4-2所示的三棱柱形物体,则图中a的值可以是( )
A. 1 B. 2 C. 3 D. 4
14. 10名工人某天生产同一个零件,个数分别是45,50,50,75,20,30,50,80,20,30.由于记件组长的不认真,经过核实,一名工人生产的80件错误,实际生产了90件,则实际生产的零件中与记录表中零件中,以下不变量为
A. 中位数与平均数 B. 众数与平均数 C. 中位数与方差 D. 中位数与众数
15.我国古代著作《增删算法统宗》中记载了一首古算诗:“林下牧童闹如簇,不知人数不知竹。每人六竿多十四,每人八竿恰齐足。”其大意是:牧童们在树下拿着竹竿高兴地玩耍,不知有多少人和竹竿。每人6竿,多14竿;每人8竿,恰好用完。若设牧童有x人,根据题意可列方程为( )
A. B.
C. D.
16.题目:如图5,,,,点P在线段AB上以2cm/s的速度由点A向点B运动,同时,点Q在射线BD上运动速度为xcm/s,它们运动的时间为t(s)(当点P运动结束时,点Q运动随之结束)。当点P,Q运动到某处时,有△ACP与△BPQ全等,求相应的x,t的值,其答案为:丽丽的答案:;轩轩的答案;笑笑的答案:,则下列说法正确的是( )
A.只有丽丽的答案正确
B.轩轩和笑笑的答案合在一起才完整
C. 丽丽与轩轩的答案合在一起才完整
D. 三人答案合在一起才完整
二、填空题(本大题有3个小题,每小题3分,共9分。其中18小题第一空2分,第二空1分;19小题每空1分。把答案写在题中横线上。)
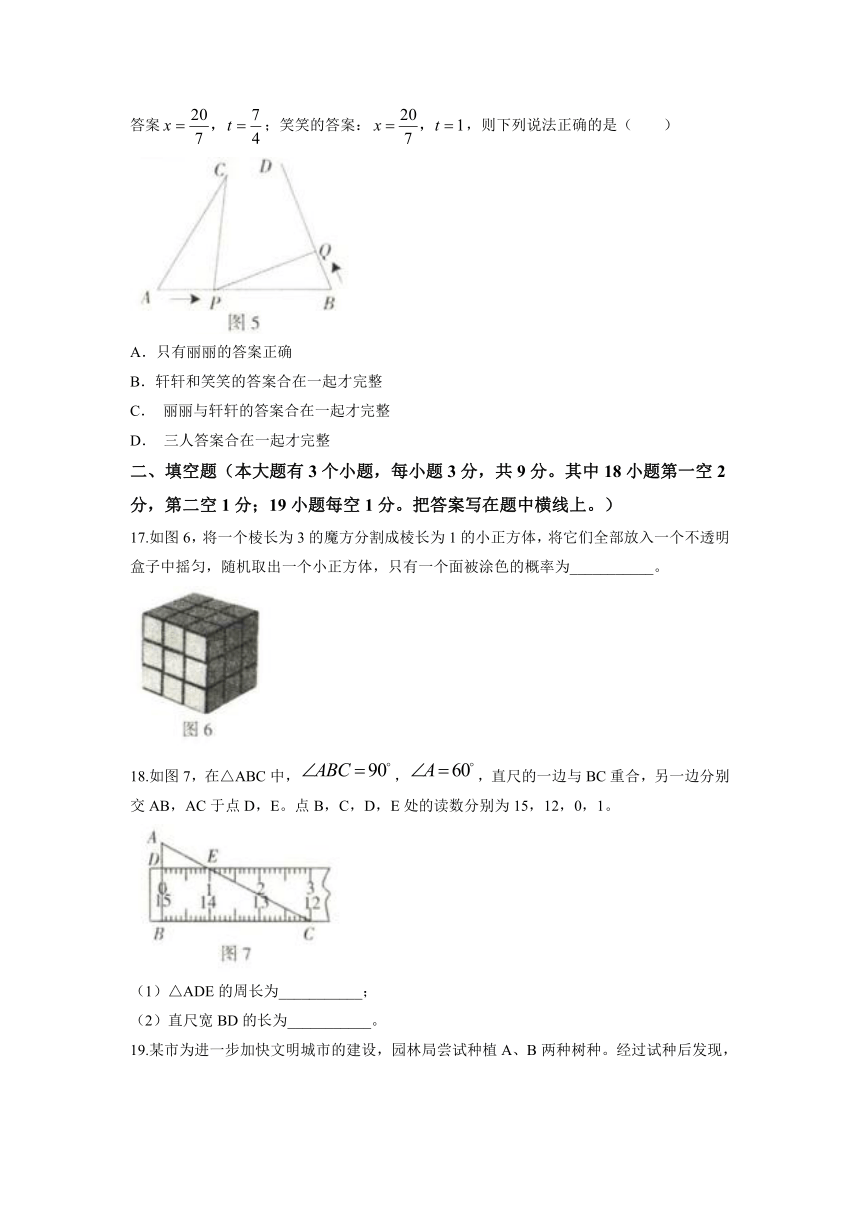
17.如图6,将一个棱长为3的魔方分割成棱长为1的小正方体,将它们全部放入一个不透明盒子中摇匀,随机取出一个小正方体,只有一个面被涂色的概率为___________。
18.如图7,在△ABC中,,,直尺的一边与BC重合,另一边分别交AB,AC于点D,E。点B,C,D,E处的读数分别为15,12,0,1。
(1)△ADE的周长为___________;
(2)直尺宽BD的长为___________。
19.某市为进一步加快文明城市的建设,园林局尝试种植A、B两种树种。经过试种后发现,种植A种树苗a棵,种下后成活了()棵,种植B种树苗b棵,种下后成活了(b-2)棵。则两种树苗的总的成活率为___________(用分子和分母各项系数都为整数的分数表示);第一阶段两种树苗共种植了40棵,且两种树苗的成活棵数相同,则种植A种树苗___________棵。第二阶段,该园林局又种植A种树苗m棵,B种树苗n棵,若,在第一阶段的基础上进行统计,则这两个阶段种植A种树苗成活棵数___________种植B种树苗成活棵数(填“>”“<”或“=”)。
三、解答题(本大题有7个小题,共69分。解答应写出文字说明、证明过程或演算步骤)
20.(本小题满分9分)
请按照如图8所示的程序:
(1)计算输出整式B的最简结果;
(2)判断整式B的值能否大于0,并说明理由。
21.(本小题满分9分)
某公司的年度综合考评由平时、年中、年末三部分考核组成,某员工的考核情况如下表所示:
考核 平时 年中 年末
类别 第1季度 第2季度 第3季度 第4季度
成绩(分) 106 102 114 I10 110 107
(1)计算该员工本年度的平时平均成绩;
(2)如果本年度的总评成绩是根据如图9所示的权重计算的,请计算出该员工本年度的总评成绩。
22.(本小题满分9分)
如果一个正整数能表示为两个连续奇数的平方差,那么称这个正整数为“友好数”。如:①;②;③,因此8,16,24都是“友好数”。
(1)9和32是“友好数”吗?为什么?
(2)若一个“友好数”能表示为两个连续奇数和(k为正整数)的平方差,则这个“友好数”是8的倍数吗?请用因式分解的方法进行说明。
23.(本小题满分10分)
已知抛物线的顶点坐标为(1,3)。
(1)求b,c的值;
(2)直线l交抛物线于点A(-2,m),B(n,2)。若点P在抛物线上且位于直线l的上方(不与点A,B重合),求点P的纵坐标的取值范围。
24.(本小题满分10分)
在古代,智慧的劳动人民已经会使用“石磨”,其原理为在磨盘的边缘连接一个固定长度的“杠杆”,推动“杠杆”带动磨盘转动,将粮食磨碎。如图10-2,AB为⊙O的直径,AC是⊙O的一条弦,D为弧BC的中点,作于点E,交AB的延长线于点F,连接DA。
(1)若,求圆心O到“杠杆EF”的距离;
(2)若,求阴影部分的面积。(结果保留π)
25.(本小题满分10分)
如图11,在平面直角坐标系中,直线经过点A(7,0)和点C(3,4),直线经过原点O和点C。
(1)求直线和直线的解析式;
(2)点D是射线OA上一动点,点O关于点D的对称点为点E,过D点作轴,交直线OC于点G,以DE,DG为邻边作矩形DEFG。
①当点F落在直线AC上时,求出OD的长;
②当△OAF为等腰三角形时,直接写出点D的坐标。
26.(本小题满分12分)
如图12-1,四边形ABCD为正方形,,点E在BA的延长线上,点F在AD上,,。如图12-2,将△AEF绕点A顺时针旋转x度得到△
(1)如图12-2,连接,,判断线段与线段之间的关系,并说明理由;
(2)如图12-3,连接。若,求的最小值和最大值;
(3)如图12-4,直线与直线交于点N,连接CN。若,求CN的长。
2023年河北省中考适应性模拟检测
数学试卷(导向一)参考答案
本答案仅供参考,若考生答案与本答案不一致,只要正确,同样得分。
一、选择题
题号 1 2 3 4 5 6 7 8
答案 D B B D D C B C
题号 9 10 11 12 13 14 15 16
答案 B A A D C D A C
二、填空题
17.
18.(1)1+;(2)
19.;22;>
三、解答题
20.解:(1)根据题意得:
(2)整式B的值不能大于0。
理由如下:
∴整式B的值不能大于0。
21.解:(1)由题意可知:
∴该员工本年度的平时平均成绩为108分;
(2)
∴该员工本年度的总评成绩为108分;
22.解:(1)9不是“友好数”,32是“友好数”
理由:∵,但是4不是奇数。
∴9不是“友好数”;
∵,是两个连续奇数的平方差,
∴32是“友好数”;
(2)∵
∴两个连续奇数和2k-1(k为正整数)的平方差是8的倍数。
23.解:(1)∵抛物线的顶点坐标为(1,3)。
∴顶点式为
∵
∴
(2)由(1)可知抛物线为:,
∴直线l交抛物线于点A(-2,m),B(n,2),
将代入,
得,即,
∴点A的坐标为(-2,-6)
将代入,
得,
解得或2,即或2。
∴点B坐标为(0,2)或(2,2),
方法一:如图所示:
由题意可得点P的纵坐标的取值范围为
方法二:
①点A坐标为(-2,-6),点B坐标为(0,2),
设直线l的解析式为,
将(-2,-6)和(0,2)代入,
得解得
∴直线l的解析式为。
∵点P在抛物线上且位于直线l的上方(不与点A,B重合),
设点P坐标为(,),
∴,
解得。
∵二次函数对称轴为,开口向下,
∴在时,随的增大而增大,
∴。。。
②点A坐标为(-2,-6),点B坐标为(2,2),
设直线l的解析式为
将(-2,-6)和(2,2)代入
得,解得
∴直线l的解析式为。
∵点P在抛物线上且位于直线l的上方(不与点A,B重合),
设点P坐标为(xp,),
∴
解得
∵二次函数对称轴为,开口向下,
∴在时,随的增大而增大,在时,随的增大而减小,
∴
综上,点P的纵坐标的取值范围为。。
24.解:(1)连接OD,如图。
∵D为弧BC的中点,
∴,
∵,
∴,
∴,
∴
∵,
∴,
∴,
∴。
∴OD的长是圆心O到“杠杆EF”的距离。
∵,
∴。
(2)∵·,
∴
由(1)得:,
∴
∵,
∴,
∴,
在Rt△FOD中,,,
∴,解得,
∴。
25.解:(1)将点A(7,0)和点C(3,4)代入,得
解得:。
将点C(3,4)代入,得,解得。
∴;
(2)①设点D(a,0),则G(a,a),E(2a,0),
当时,。
∵四边形DEFG是矩形,
∴,
∴点G和F的纵坐标相等,
∴∴,∴;
②点D(,0)或(,0)或(,0)
提示:F(2a,a),A(7,0),
当时,,∴,∴D(,0)。
当时,
∴∵D(,0)
当时,,
∴
∴D(,0)
综上所述:点D(,0)或(,0)或(,0)。
26.解:(1),且。
理由:∵四边形ABCD是正方形,
∴
∵,
∴
又,
∴
在△DE'A和△BF'A中,
∴
∴。
延长BF'交AD于H,交DE'于G,如图1,
∵
∴
∴,
∴。
综上,线段DE'与线段BF'之间的关系为,且:。
(2)根据题意知,E',F'点在以A为圆心,AE'为半径的圆上运动,如图2,
当在AC上时,的值最小,
当在CA的延长线上时,CF'的值最大。
∵,
又,
∴的最小值为
最大值为。
(3)由(1)知,,连接BD,如图3,
在Rt△BCD中,,
∴
∵∴
在Rt△DBN中,,
∴,
∴。
∵,,,
易证得A,D,N,B,C五点在同一个圆上,如图3,设AD与CN交于点M,
∴,
又,
∴∴
∴
∴
∴
连接AC,则
∴,
∴
∴。
2023年河北省中考适应性模拟检测
数学试卷(导向一)
(考试时间:120分钟,满分:120分)
一、选择题(本大题共16个小题,1~10小题每题3分;11~16小题每题2分,共42分。在每小题给出的四个选项中,只有一项是符合题目要求的)
1.若则m值为。( )
A. 8 B. 6 C. 5 D. 2
2. 如图1,在△ABC中,D为AC上一点,把△DBC沿BD折叠,使点C落在AC上的点E处,则BD是△ABC的
A. 中线 B. 高线
C. 角平分线 D. 对角线
3.下列各式中的计算结果与相等的是。( )
A. B. C. D.
4.下列各式中正确的是
A. B C. D.
5.一个多边形的内角和为α,外角和为β,则的多边形的是( )
A. B.
C. D.
6. 华为最新款手机芯片“麒麟”是一种微型处理器,每秒可进行100亿次运算,它工作2023秒可进行的运算次数用科学记数法表示为
A. B.
C. D.
7.如图2所示,下列几何体中能同时堵住图中三个空洞的几何体是
A. B.
C. D.
8.张师傅应客户要求加工4个菱形零件。在交付客户之前,张师傅需要对4个零件进行检测。根据零件的。检测结果,图中有可能不合格的零件是
A. B.
C. D.
9.如图3,圆形挂钟分针针尖到圆心的距离为10cm,经过20分钟,分针针尖转过的弧长是( )
A.π cm B.πcm
C.π cm D.πcm
10.某同学的。作业如下框,其中*处填。的依据是
如图,已知直线、,,,若,则,
请完成下面的说理过程。
解:∵,
∴
∴(两直线平行,同位角相等)
A. 内错角相等,两直线平行 B. 同位角相等,两直线平行
C. 两直线平行,内错角相等 D. 两直线平行,同位角相等
11. 如果,那么的值是( )
A. 3 B. -3 C. D.
12. 在股票买卖过程中,经常用到两种曲线,一种是即时价格曲线,一种是平均价格曲线(如表示开始交易后第2小时的即时价格为3元;表示开始交易后两个小时内所有成交股票的平均价格为4元)。下面所给出的四个图象中,实线表示,虚线表示,其中可能正确的是
A. B.
C. D.
13. 如图4-1所示,将长为8的矩形纸片沿虚线折成3个矩形,其中左右两侧矩形的宽相等。若要将其围成如图4-2所示的三棱柱形物体,则图中a的值可以是( )
A. 1 B. 2 C. 3 D. 4
14. 10名工人某天生产同一个零件,个数分别是45,50,50,75,20,30,50,80,20,30.由于记件组长的不认真,经过核实,一名工人生产的80件错误,实际生产了90件,则实际生产的零件中与记录表中零件中,以下不变量为
A. 中位数与平均数 B. 众数与平均数 C. 中位数与方差 D. 中位数与众数
15.我国古代著作《增删算法统宗》中记载了一首古算诗:“林下牧童闹如簇,不知人数不知竹。每人六竿多十四,每人八竿恰齐足。”其大意是:牧童们在树下拿着竹竿高兴地玩耍,不知有多少人和竹竿。每人6竿,多14竿;每人8竿,恰好用完。若设牧童有x人,根据题意可列方程为( )
A. B.
C. D.
16.题目:如图5,,,,点P在线段AB上以2cm/s的速度由点A向点B运动,同时,点Q在射线BD上运动速度为xcm/s,它们运动的时间为t(s)(当点P运动结束时,点Q运动随之结束)。当点P,Q运动到某处时,有△ACP与△BPQ全等,求相应的x,t的值,其答案为:丽丽的答案:;轩轩的答案;笑笑的答案:,则下列说法正确的是( )
A.只有丽丽的答案正确
B.轩轩和笑笑的答案合在一起才完整
C. 丽丽与轩轩的答案合在一起才完整
D. 三人答案合在一起才完整
二、填空题(本大题有3个小题,每小题3分,共9分。其中18小题第一空2分,第二空1分;19小题每空1分。把答案写在题中横线上。)
17.如图6,将一个棱长为3的魔方分割成棱长为1的小正方体,将它们全部放入一个不透明盒子中摇匀,随机取出一个小正方体,只有一个面被涂色的概率为___________。
18.如图7,在△ABC中,,,直尺的一边与BC重合,另一边分别交AB,AC于点D,E。点B,C,D,E处的读数分别为15,12,0,1。
(1)△ADE的周长为___________;
(2)直尺宽BD的长为___________。
19.某市为进一步加快文明城市的建设,园林局尝试种植A、B两种树种。经过试种后发现,种植A种树苗a棵,种下后成活了()棵,种植B种树苗b棵,种下后成活了(b-2)棵。则两种树苗的总的成活率为___________(用分子和分母各项系数都为整数的分数表示);第一阶段两种树苗共种植了40棵,且两种树苗的成活棵数相同,则种植A种树苗___________棵。第二阶段,该园林局又种植A种树苗m棵,B种树苗n棵,若,在第一阶段的基础上进行统计,则这两个阶段种植A种树苗成活棵数___________种植B种树苗成活棵数(填“>”“<”或“=”)。
三、解答题(本大题有7个小题,共69分。解答应写出文字说明、证明过程或演算步骤)
20.(本小题满分9分)
请按照如图8所示的程序:
(1)计算输出整式B的最简结果;
(2)判断整式B的值能否大于0,并说明理由。
21.(本小题满分9分)
某公司的年度综合考评由平时、年中、年末三部分考核组成,某员工的考核情况如下表所示:
考核 平时 年中 年末
类别 第1季度 第2季度 第3季度 第4季度
成绩(分) 106 102 114 I10 110 107
(1)计算该员工本年度的平时平均成绩;
(2)如果本年度的总评成绩是根据如图9所示的权重计算的,请计算出该员工本年度的总评成绩。
22.(本小题满分9分)
如果一个正整数能表示为两个连续奇数的平方差,那么称这个正整数为“友好数”。如:①;②;③,因此8,16,24都是“友好数”。
(1)9和32是“友好数”吗?为什么?
(2)若一个“友好数”能表示为两个连续奇数和(k为正整数)的平方差,则这个“友好数”是8的倍数吗?请用因式分解的方法进行说明。
23.(本小题满分10分)
已知抛物线的顶点坐标为(1,3)。
(1)求b,c的值;
(2)直线l交抛物线于点A(-2,m),B(n,2)。若点P在抛物线上且位于直线l的上方(不与点A,B重合),求点P的纵坐标的取值范围。
24.(本小题满分10分)
在古代,智慧的劳动人民已经会使用“石磨”,其原理为在磨盘的边缘连接一个固定长度的“杠杆”,推动“杠杆”带动磨盘转动,将粮食磨碎。如图10-2,AB为⊙O的直径,AC是⊙O的一条弦,D为弧BC的中点,作于点E,交AB的延长线于点F,连接DA。
(1)若,求圆心O到“杠杆EF”的距离;
(2)若,求阴影部分的面积。(结果保留π)
25.(本小题满分10分)
如图11,在平面直角坐标系中,直线经过点A(7,0)和点C(3,4),直线经过原点O和点C。
(1)求直线和直线的解析式;
(2)点D是射线OA上一动点,点O关于点D的对称点为点E,过D点作轴,交直线OC于点G,以DE,DG为邻边作矩形DEFG。
①当点F落在直线AC上时,求出OD的长;
②当△OAF为等腰三角形时,直接写出点D的坐标。
26.(本小题满分12分)
如图12-1,四边形ABCD为正方形,,点E在BA的延长线上,点F在AD上,,。如图12-2,将△AEF绕点A顺时针旋转x度得到△
(1)如图12-2,连接,,判断线段与线段之间的关系,并说明理由;
(2)如图12-3,连接。若,求的最小值和最大值;
(3)如图12-4,直线与直线交于点N,连接CN。若,求CN的长。
2023年河北省中考适应性模拟检测
数学试卷(导向一)参考答案
本答案仅供参考,若考生答案与本答案不一致,只要正确,同样得分。
一、选择题
题号 1 2 3 4 5 6 7 8
答案 D B B D D C B C
题号 9 10 11 12 13 14 15 16
答案 B A A D C D A C
二、填空题
17.
18.(1)1+;(2)
19.;22;>
三、解答题
20.解:(1)根据题意得:
(2)整式B的值不能大于0。
理由如下:
∴整式B的值不能大于0。
21.解:(1)由题意可知:
∴该员工本年度的平时平均成绩为108分;
(2)
∴该员工本年度的总评成绩为108分;
22.解:(1)9不是“友好数”,32是“友好数”
理由:∵,但是4不是奇数。
∴9不是“友好数”;
∵,是两个连续奇数的平方差,
∴32是“友好数”;
(2)∵
∴两个连续奇数和2k-1(k为正整数)的平方差是8的倍数。
23.解:(1)∵抛物线的顶点坐标为(1,3)。
∴顶点式为
∵
∴
(2)由(1)可知抛物线为:,
∴直线l交抛物线于点A(-2,m),B(n,2),
将代入,
得,即,
∴点A的坐标为(-2,-6)
将代入,
得,
解得或2,即或2。
∴点B坐标为(0,2)或(2,2),
方法一:如图所示:
由题意可得点P的纵坐标的取值范围为
方法二:
①点A坐标为(-2,-6),点B坐标为(0,2),
设直线l的解析式为,
将(-2,-6)和(0,2)代入,
得解得
∴直线l的解析式为。
∵点P在抛物线上且位于直线l的上方(不与点A,B重合),
设点P坐标为(,),
∴,
解得。
∵二次函数对称轴为,开口向下,
∴在时,随的增大而增大,
∴。。。
②点A坐标为(-2,-6),点B坐标为(2,2),
设直线l的解析式为
将(-2,-6)和(2,2)代入
得,解得
∴直线l的解析式为。
∵点P在抛物线上且位于直线l的上方(不与点A,B重合),
设点P坐标为(xp,),
∴
解得
∵二次函数对称轴为,开口向下,
∴在时,随的增大而增大,在时,随的增大而减小,
∴
综上,点P的纵坐标的取值范围为。。
24.解:(1)连接OD,如图。
∵D为弧BC的中点,
∴,
∵,
∴,
∴,
∴
∵,
∴,
∴,
∴。
∴OD的长是圆心O到“杠杆EF”的距离。
∵,
∴。
(2)∵·,
∴
由(1)得:,
∴
∵,
∴,
∴,
在Rt△FOD中,,,
∴,解得,
∴。
25.解:(1)将点A(7,0)和点C(3,4)代入,得
解得:。
将点C(3,4)代入,得,解得。
∴;
(2)①设点D(a,0),则G(a,a),E(2a,0),
当时,。
∵四边形DEFG是矩形,
∴,
∴点G和F的纵坐标相等,
∴∴,∴;
②点D(,0)或(,0)或(,0)
提示:F(2a,a),A(7,0),
当时,,∴,∴D(,0)。
当时,
∴∵D(,0)
当时,,
∴
∴D(,0)
综上所述:点D(,0)或(,0)或(,0)。
26.解:(1),且。
理由:∵四边形ABCD是正方形,
∴
∵,
∴
又,
∴
在△DE'A和△BF'A中,
∴
∴。
延长BF'交AD于H,交DE'于G,如图1,
∵
∴
∴,
∴。
综上,线段DE'与线段BF'之间的关系为,且:。
(2)根据题意知,E',F'点在以A为圆心,AE'为半径的圆上运动,如图2,
当在AC上时,的值最小,
当在CA的延长线上时,CF'的值最大。
∵,
又,
∴的最小值为
最大值为。
(3)由(1)知,,连接BD,如图3,
在Rt△BCD中,,
∴
∵∴
在Rt△DBN中,,
∴,
∴。
∵,,,
易证得A,D,N,B,C五点在同一个圆上,如图3,设AD与CN交于点M,
∴,
又,
∴∴
∴
∴
∴
连接AC,则
∴,
∴
∴。
同课章节目录
