人教版数学八年级下册 18.2特殊的平行四边形 同步练习(含答案)
文档属性
| 名称 | 人教版数学八年级下册 18.2特殊的平行四边形 同步练习(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 149.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-08 00:00:00 | ||
图片预览

文档简介
人教版数学八年级下册 18.2特殊的平行四边形
一、单选题
1.下列命题正确的是( )
A.一组邻边相等的四边形是菱形
B.对角线互相垂直的四边形是菱形
C.对角线互相垂直且相等的四边形是菱形
D.对角线互相垂直且平分的四边形是菱形
2.如图,四边形ABCD是平行四边形,下列说法不正确的是( )
A.当AC=BD时,四边形ABCD是矩形
B.当AB=BC时,四边形ABCD是菱形
C.当AC⊥BD时,四边形ABCD是菱形
D.当∠DAB=90°时,四边形ABCD是正方形
3.下列条件中,不能判定四边形ABCD为菱形的是( ).
A.AC⊥BD,AC与BD互相平分 B.AB=BC=CD=DA
C.AB=BC,AD=CD,且AC⊥BD D.AB=CD,AD=BC,AC⊥BD
4.如图,在 ABCD中,AB>2BC,观察图中尺规作图的痕迹,则下列结论错误的是( )
A.BG平分∠ABC B.BE=BF C.AD=CH D.CH=DH
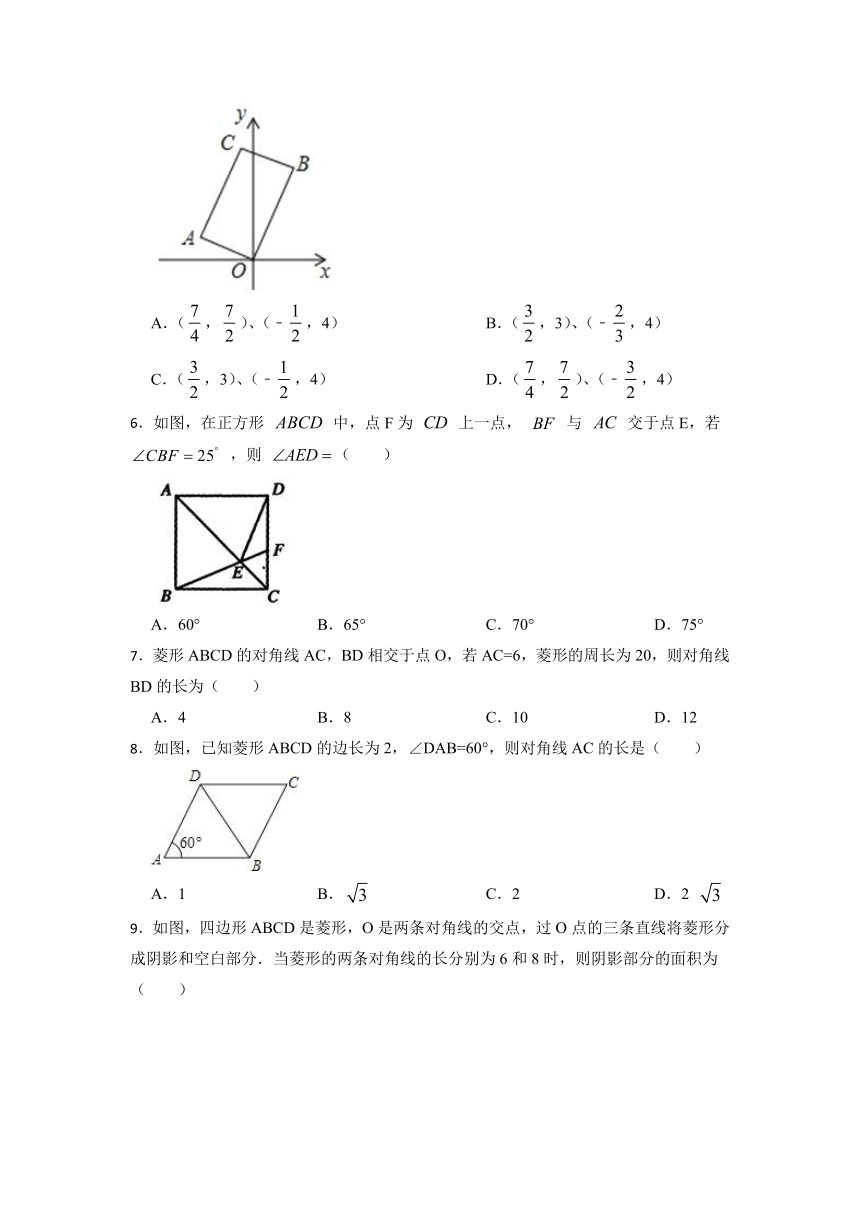
5.如图,在矩形AOBC中,点A的坐标(﹣2,1),点C的纵坐标是4,则B、C两点的坐标分别是( )
A.(,)、(﹣,4) B.(,3)、(﹣,4)
C.(,3)、(﹣,4) D.(,)、(﹣,4)
6.如图,在正方形 中,点F为 上一点, 与 交于点E,若 ,则 ( )
A.60° B.65° C.70° D.75°
7.菱形ABCD的对角线AC,BD相交于点O,若AC=6,菱形的周长为20,则对角线BD的长为( )
A.4 B.8 C.10 D.12
8.如图,已知菱形ABCD的边长为2,∠DAB=60°,则对角线AC的长是( )
A.1 B. C.2 D.2
9.如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分.当菱形的两条对角线的长分别为6和8时,则阴影部分的面积为( )
A.24 cm2 B.20 cm2 C.16 cm2 D.12 cm2
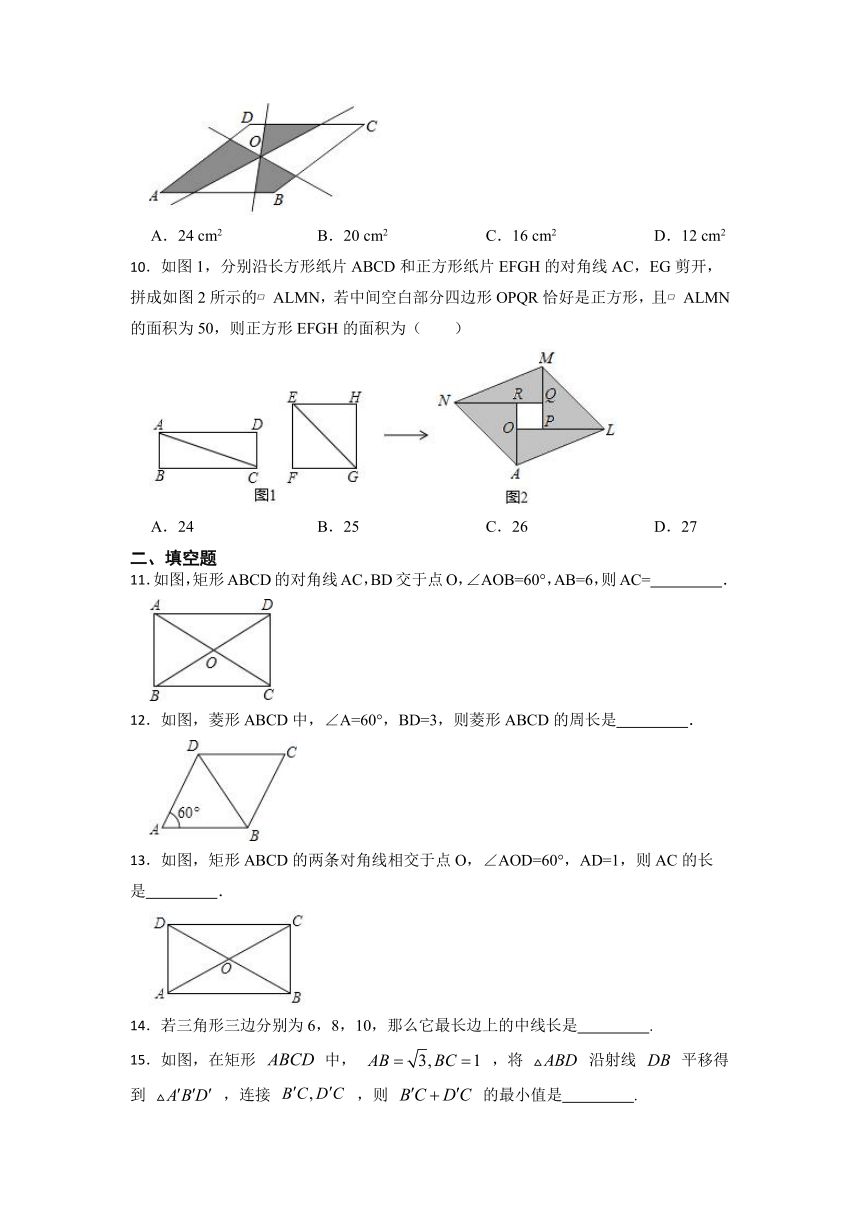
10.如图1,分别沿长方形纸片ABCD和正方形纸片EFGH的对角线AC,EG剪开,拼成如图2所示的 ALMN,若中间空白部分四边形OPQR恰好是正方形,且 ALMN的面积为50,则正方形EFGH的面积为( )
A.24 B.25 C.26 D.27
二、填空题
11.如图,矩形ABCD的对角线AC,BD交于点O,∠AOB=60°,AB=6,则AC= .
12.如图,菱形ABCD中,∠A=60°,BD=3,则菱形ABCD的周长是 .
13.如图,矩形ABCD的两条对角线相交于点O,∠AOD=60°,AD=1,则AC的长是 .
14.若三角形三边分别为6,8,10,那么它最长边上的中线长是 .
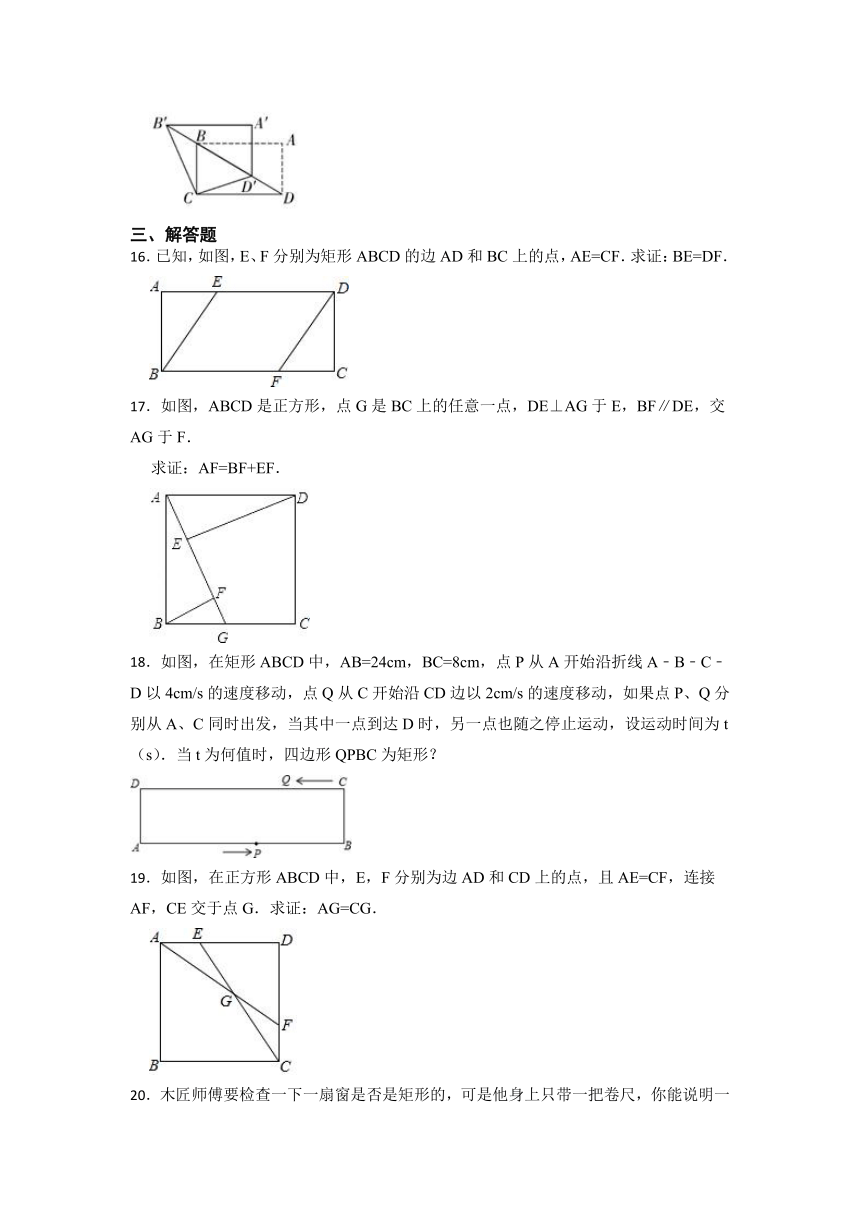
15.如图,在矩形 中, ,将 沿射线 平移得到 ,连接 ,则 的最小值是 .
三、解答题
16.已知,如图,E、F分别为矩形ABCD的边AD和BC上的点,AE=CF.求证:BE=DF.
17.如图,ABCD是正方形,点G是BC上的任意一点,DE⊥AG于E,BF∥DE,交AG于F.
求证:AF=BF+EF.
18.如图,在矩形ABCD中,AB=24cm,BC=8cm,点P从A开始沿折线A﹣B﹣C﹣D以4cm/s的速度移动,点Q从C开始沿CD边以2cm/s的速度移动,如果点P、Q分别从A、C同时出发,当其中一点到达D时,另一点也随之停止运动,设运动时间为t(s).当t为何值时,四边形QPBC为矩形?
19.如图,在正方形ABCD中,E,F分别为边AD和CD上的点,且AE=CF,连接AF,CE交于点G.求证:AG=CG.
20.木匠师傅要检查一下一扇窗是否是矩形的,可是他身上只带一把卷尺,你能说明一下木匠师傅可以用什么样的方法进行检验吗?请你说明这样操作的依据是什么?
21.如图,已知在菱形ABCD中,∠ABC=60°,对角线AC=8,求菱形ABCD的周长和面积.
22.(感知)如图①,四边形ABCD、CEFG均为正方形.可知BE=DG.
(拓展)如图②,四边形ABCD、CEFG均为菱形,且∠A=∠F.求证:BE=DG.
(应用)如图③,四边形ABCD、CEFG均为菱形,点E在边AD上,点G在AD延长线上.若AE=2ED,∠A=∠F,△EBC的面积为8,菱形CEFG的面积是 .(只填结果)
答案解析部分
1.【答案】D
2.【答案】D
3.【答案】C
4.【答案】D
5.【答案】C
6.【答案】C
7.【答案】B
8.【答案】D
9.【答案】D
10.【答案】B
11.【答案】12
12.【答案】12
13.【答案】2
14.【答案】5
15.【答案】
16.【答案】证明:证法一:∵四边形ABCD为矩形,
∴AB=CD,∠A=∠C=90°.
在△ABE和△CDF中
∵ , ∴△ABE≌△CDF(SAS),
∴BE=DF(全等三角形对应边相等)
证法二:∵四边形ABCD为矩形,
∴AD∥BC,AD=BC,
又∵AE=CF,∴AD-AE=BC-CF
即ED=BF,
而ED∥BF,
∴四边形BFDE为平行四边形
∴BE=DF(平行四边形对边相等).
利用全等三角形对应边相等求证
17.【答案】证明:∵ABCD是正方形,∴AD=AB,∠BAD=90°,∵DE⊥AG,∴∠DEG=∠AED=90°,∴∠ADE+∠DAE=90°,又∵∠BAF+∠DAE=∠BAD=90°,∴∠ADE=∠BAF.∵BF∥DE,∴∠AFB=∠DEG=∠AED.在△ABF与△DAE中, ,∴△ABF≌△DAE(AAS).∴BF=AE.∵AF=AE+EF,∴AF=BF+EF.
18.【答案】解:根据题意得:CQ=2t,AP=4t,
则BP=24-4t,
∵四边形ABCD是矩形,
∴∠B=∠C=90°,CD∥AB,
∴只有CQ=BP时,四边形QPBC是矩形,
即2t=24-4t,
解得:t=4,
答:当t=4s时,四边形QPBC是矩形.
19.【答案】证明:∵四边形ABCD是正方形,
∴∠ADF=CDE=90°,AD=CD.
∵AE=CF,
∴DE=DF,
在△ADF和△CDE中 ,
∴△ADF≌△CDE(SAS),
∴∠DAF=∠DCE,
在△AGE和△CGF中, ,
∴△AGE≌△CGF(AAS),
∴AG=CG.
20.【答案】解:可以先用卷尺测量一下这个四边形的两组对边是否相等,如果相等,那么这个四边形就是平行四边形,再用卷尺测量这个四边形的两条对角线是否相等,如果相等那么这个平行四边形就是矩形
21.【答案】∵四边形ABCD是菱形,
∴AB=BC,
∵∠ABC=60°,
∴△ABC是等边三角形,
∴AB=AC=8.
∴菱形ABCD的周长=4×8=32,
∵BO= =4 ,
∴BD=2BO=8 ,
∴菱形ABCD的面积= ×8× =32 .
22.【答案】拓展:证明:∵四边形ABCD、四边形CEFG均为菱形,∴BC=CD,CE=CG,∠BCD=∠A,∠ECG=∠F.∵∠A=∠F,∴∠BCD=∠ECG.∴∠BCD-∠ECD=∠ECG-∠ECD,即∠BCE=∠DCG.在△BCE和△DCG中,∴△BCE≌△DCG(SAS),∴BE=DG.应用: 20
一、单选题
1.下列命题正确的是( )
A.一组邻边相等的四边形是菱形
B.对角线互相垂直的四边形是菱形
C.对角线互相垂直且相等的四边形是菱形
D.对角线互相垂直且平分的四边形是菱形
2.如图,四边形ABCD是平行四边形,下列说法不正确的是( )
A.当AC=BD时,四边形ABCD是矩形
B.当AB=BC时,四边形ABCD是菱形
C.当AC⊥BD时,四边形ABCD是菱形
D.当∠DAB=90°时,四边形ABCD是正方形
3.下列条件中,不能判定四边形ABCD为菱形的是( ).
A.AC⊥BD,AC与BD互相平分 B.AB=BC=CD=DA
C.AB=BC,AD=CD,且AC⊥BD D.AB=CD,AD=BC,AC⊥BD
4.如图,在 ABCD中,AB>2BC,观察图中尺规作图的痕迹,则下列结论错误的是( )
A.BG平分∠ABC B.BE=BF C.AD=CH D.CH=DH
5.如图,在矩形AOBC中,点A的坐标(﹣2,1),点C的纵坐标是4,则B、C两点的坐标分别是( )
A.(,)、(﹣,4) B.(,3)、(﹣,4)
C.(,3)、(﹣,4) D.(,)、(﹣,4)
6.如图,在正方形 中,点F为 上一点, 与 交于点E,若 ,则 ( )
A.60° B.65° C.70° D.75°
7.菱形ABCD的对角线AC,BD相交于点O,若AC=6,菱形的周长为20,则对角线BD的长为( )
A.4 B.8 C.10 D.12
8.如图,已知菱形ABCD的边长为2,∠DAB=60°,则对角线AC的长是( )
A.1 B. C.2 D.2
9.如图,四边形ABCD是菱形,O是两条对角线的交点,过O点的三条直线将菱形分成阴影和空白部分.当菱形的两条对角线的长分别为6和8时,则阴影部分的面积为( )
A.24 cm2 B.20 cm2 C.16 cm2 D.12 cm2
10.如图1,分别沿长方形纸片ABCD和正方形纸片EFGH的对角线AC,EG剪开,拼成如图2所示的 ALMN,若中间空白部分四边形OPQR恰好是正方形,且 ALMN的面积为50,则正方形EFGH的面积为( )
A.24 B.25 C.26 D.27
二、填空题
11.如图,矩形ABCD的对角线AC,BD交于点O,∠AOB=60°,AB=6,则AC= .
12.如图,菱形ABCD中,∠A=60°,BD=3,则菱形ABCD的周长是 .
13.如图,矩形ABCD的两条对角线相交于点O,∠AOD=60°,AD=1,则AC的长是 .
14.若三角形三边分别为6,8,10,那么它最长边上的中线长是 .
15.如图,在矩形 中, ,将 沿射线 平移得到 ,连接 ,则 的最小值是 .
三、解答题
16.已知,如图,E、F分别为矩形ABCD的边AD和BC上的点,AE=CF.求证:BE=DF.
17.如图,ABCD是正方形,点G是BC上的任意一点,DE⊥AG于E,BF∥DE,交AG于F.
求证:AF=BF+EF.
18.如图,在矩形ABCD中,AB=24cm,BC=8cm,点P从A开始沿折线A﹣B﹣C﹣D以4cm/s的速度移动,点Q从C开始沿CD边以2cm/s的速度移动,如果点P、Q分别从A、C同时出发,当其中一点到达D时,另一点也随之停止运动,设运动时间为t(s).当t为何值时,四边形QPBC为矩形?
19.如图,在正方形ABCD中,E,F分别为边AD和CD上的点,且AE=CF,连接AF,CE交于点G.求证:AG=CG.
20.木匠师傅要检查一下一扇窗是否是矩形的,可是他身上只带一把卷尺,你能说明一下木匠师傅可以用什么样的方法进行检验吗?请你说明这样操作的依据是什么?
21.如图,已知在菱形ABCD中,∠ABC=60°,对角线AC=8,求菱形ABCD的周长和面积.
22.(感知)如图①,四边形ABCD、CEFG均为正方形.可知BE=DG.
(拓展)如图②,四边形ABCD、CEFG均为菱形,且∠A=∠F.求证:BE=DG.
(应用)如图③,四边形ABCD、CEFG均为菱形,点E在边AD上,点G在AD延长线上.若AE=2ED,∠A=∠F,△EBC的面积为8,菱形CEFG的面积是 .(只填结果)
答案解析部分
1.【答案】D
2.【答案】D
3.【答案】C
4.【答案】D
5.【答案】C
6.【答案】C
7.【答案】B
8.【答案】D
9.【答案】D
10.【答案】B
11.【答案】12
12.【答案】12
13.【答案】2
14.【答案】5
15.【答案】
16.【答案】证明:证法一:∵四边形ABCD为矩形,
∴AB=CD,∠A=∠C=90°.
在△ABE和△CDF中
∵ , ∴△ABE≌△CDF(SAS),
∴BE=DF(全等三角形对应边相等)
证法二:∵四边形ABCD为矩形,
∴AD∥BC,AD=BC,
又∵AE=CF,∴AD-AE=BC-CF
即ED=BF,
而ED∥BF,
∴四边形BFDE为平行四边形
∴BE=DF(平行四边形对边相等).
利用全等三角形对应边相等求证
17.【答案】证明:∵ABCD是正方形,∴AD=AB,∠BAD=90°,∵DE⊥AG,∴∠DEG=∠AED=90°,∴∠ADE+∠DAE=90°,又∵∠BAF+∠DAE=∠BAD=90°,∴∠ADE=∠BAF.∵BF∥DE,∴∠AFB=∠DEG=∠AED.在△ABF与△DAE中, ,∴△ABF≌△DAE(AAS).∴BF=AE.∵AF=AE+EF,∴AF=BF+EF.
18.【答案】解:根据题意得:CQ=2t,AP=4t,
则BP=24-4t,
∵四边形ABCD是矩形,
∴∠B=∠C=90°,CD∥AB,
∴只有CQ=BP时,四边形QPBC是矩形,
即2t=24-4t,
解得:t=4,
答:当t=4s时,四边形QPBC是矩形.
19.【答案】证明:∵四边形ABCD是正方形,
∴∠ADF=CDE=90°,AD=CD.
∵AE=CF,
∴DE=DF,
在△ADF和△CDE中 ,
∴△ADF≌△CDE(SAS),
∴∠DAF=∠DCE,
在△AGE和△CGF中, ,
∴△AGE≌△CGF(AAS),
∴AG=CG.
20.【答案】解:可以先用卷尺测量一下这个四边形的两组对边是否相等,如果相等,那么这个四边形就是平行四边形,再用卷尺测量这个四边形的两条对角线是否相等,如果相等那么这个平行四边形就是矩形
21.【答案】∵四边形ABCD是菱形,
∴AB=BC,
∵∠ABC=60°,
∴△ABC是等边三角形,
∴AB=AC=8.
∴菱形ABCD的周长=4×8=32,
∵BO= =4 ,
∴BD=2BO=8 ,
∴菱形ABCD的面积= ×8× =32 .
22.【答案】拓展:证明:∵四边形ABCD、四边形CEFG均为菱形,∴BC=CD,CE=CG,∠BCD=∠A,∠ECG=∠F.∵∠A=∠F,∴∠BCD=∠ECG.∴∠BCD-∠ECD=∠ECG-∠ECD,即∠BCE=∠DCG.在△BCE和△DCG中,∴△BCE≌△DCG(SAS),∴BE=DG.应用: 20
