人教版九年级上册 第二十三章 旋转 综合素质评价(含答案)
文档属性
| 名称 | 人教版九年级上册 第二十三章 旋转 综合素质评价(含答案) | 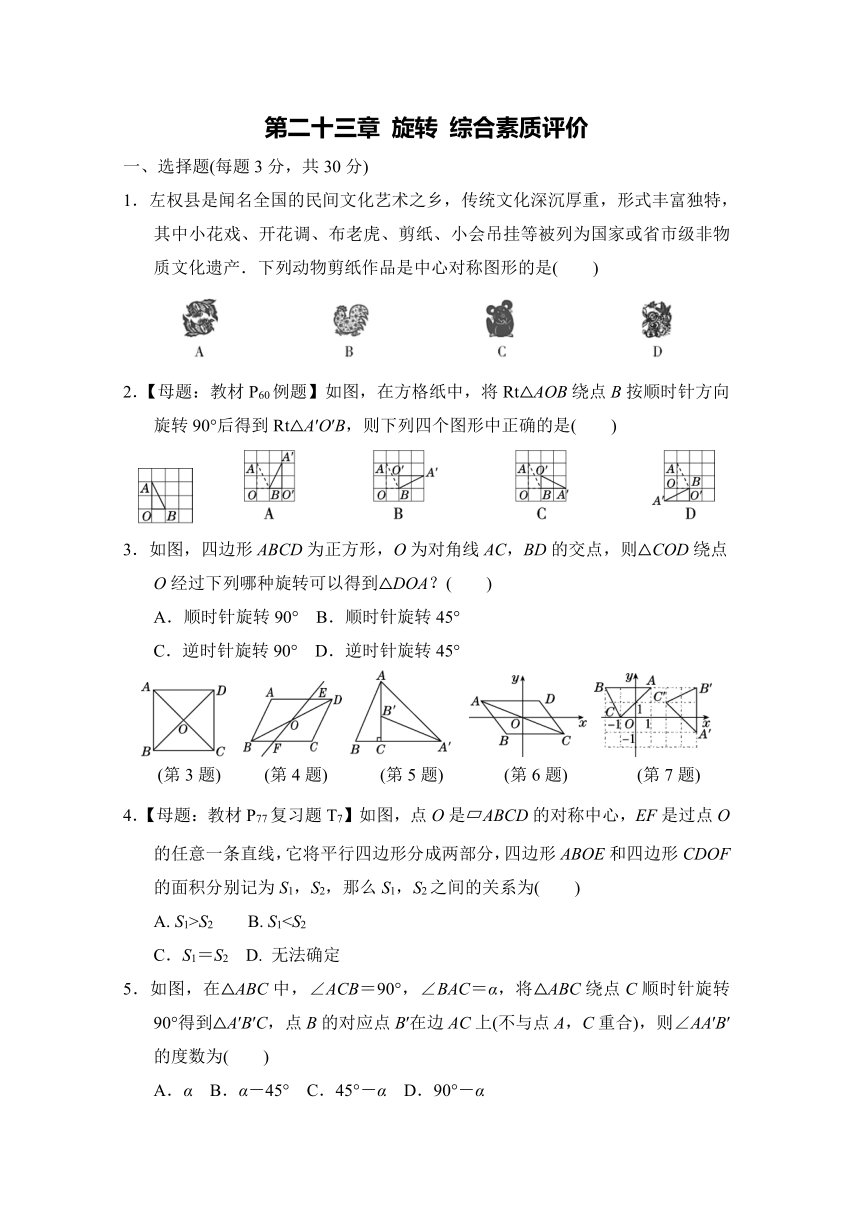 | |
| 格式 | doc | ||
| 文件大小 | 301.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-09 11:06:11 | ||
图片预览





文档简介
第二十三章 旋转 综合素质评价
一、选择题(每题3分,共30分)
1.左权县是闻名全国的民间文化艺术之乡,传统文化深沉厚重,形式丰富独特,其中小花戏、开花调、布老虎、剪纸、小会吊挂等被列为国家或省市级非物质文化遗产.下列动物剪纸作品是中心对称图形的是( )
2.【母题:教材P60例题】如图,在方格纸中,将Rt△AOB绕点B按顺时针方向旋转90°后得到Rt△A′O′B,则下列四个图形中正确的是( )
INCLUDEPICTURE"EAE66.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\EAE66.tif" \* MERGEFORMATINET INCLUDEPICTURE"EAE67.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\EAE67.tif" \* MERGEFORMATINET
3.如图,四边形ABCD为正方形,O为对角线AC,BD的交点,则△COD绕点O经过下列哪种旋转可以得到△DOA?( )
A.顺时针旋转90° B.顺时针旋转45°
C.逆时针旋转90° D.逆时针旋转45°
INCLUDEPICTURE"AB143.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\AB143.tif" \* MERGEFORMATINET INCLUDEPICTURE"S2-75.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\S2-75.tif" \* MERGEFORMATINET INCLUDEPICTURE"DV48.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\DV48.tif" \* MERGEFORMATINET INCLUDEPICTURE"QR48.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\QR48.tif" \* MERGEFORMATINET INCLUDEPICTURE"F33.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\F33.tif" \* MERGEFORMATINET
(第3题) (第4题) (第5题) (第6题) (第7题)
4.【母题:教材P77复习题T7】如图,点O是 ABCD的对称中心,EF是过点O的任意一条直线,它将平行四边形分成两部分,四边形ABOE和四边形CDOF的面积分别记为S1,S2,那么S1,S2之间的关系为( )
A. S1>S2 B. S1C.S1=S2 D. 无法确定
5.如图,在△ABC中,∠ACB=90°,∠BAC=α,将△ABC绕点C顺时针旋转90°得到△A′B′C,点B的对应点B′在边AC上(不与点A,C重合),则∠AA′B′的度数为( )
A.α B.α-45° C.45°-α D.90°-α
6.如图,在平面直角坐标系中,把△ABC绕原点O旋转180°得到△CDA,点A,B,C的坐标分别为(-5,2),(-2,-2),(5,-2),则点D的坐标为( )
A.(2,2) B.(2,-2) C.(2,5) D.(-2,5)
7.如图,在平面直角坐标系中,△ABC绕旋转中心顺时针旋转90°后得到△A′B′C′,则其旋转中心的坐标是( )
A.(1.5,1.5) B.(1,0) C.(1,-1) D.(1.5,-0.5)
8.如图,四边形ABCD是边长为5的正方形,E是DC上一点,DE=1,将△ADE绕点A顺时针旋转到与△ABF重合,则EF=( )
A. B. C.5 D.2
INCLUDEPICTURE"XZK140.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\XZK140.tif" \* MERGEFORMATINET INCLUDEPICTURE"QR44.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\QR44.tif" \* MERGEFORMATINET INCLUDEPICTURE"1A83.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\1A83.tif" \* MERGEFORMATINET INCLUDEPICTURE"APP21.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\APP21.tif" \* MERGEFORMATINET INCLUDEPICTURE"AB289.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\AB289.tif" \* MERGEFORMATINET
(第8题) (第9题) (第10题) (第12题) (第13题)
9.如图,在平面直角坐标系中,点A,C在x轴上,点C的坐标为(-1,0),AC=2,将Rt△ABC先绕点C顺时针旋转90°,再向右平移3个单位长度,则变换后点A的对应点的坐标是( )
A.(2,2) B.(1,2) C.(-1,2) D.(2,-1)
10.【2022·杭州】如图,在平面直角坐标系中,已知点P(0,2),点A(4,2).以点P为旋转中心,把点A按逆时针方向旋转60°,得点B.在M1,M2(-,-1),M3(1,4),M4四个点中,直线PB经过的点是( )
A.M1 B.M2 C.M3 D.M4
二、填空题(每题3分,共24分)
11.【2022·云南】点A(1,-5)关于原点的对称点为点B,则点B的坐标为________.
12.如图所示的雪花图案围绕旋转中心至少旋转________后可以完全重合.
13.如图,大圆的面积为4π,大圆的两条直径互相垂直,则图中阴影部分的面积的和为________.
14.如图是一个中心对称图形,A为对称中心,若∠C=90°,∠B=30°,AC=3,则BB′的长为________.
INCLUDEPICTURE"X163a.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\X163a.tif" \* MERGEFORMATINET INCLUDEPICTURE"X163.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\X163.tif" \* MERGEFORMATINET INCLUDEPICTURE"CO85.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\CO85.tif" \* MERGEFORMATINET INCLUDEPICTURE"CO86.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\CO86.tif" \* MERGEFORMATINET INCLUDEPICTURE"1A81.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\1A81.tif" \* MERGEFORMATINET
(第14题) (第15题) (第16题) (第17题) (第18题)
15.如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°).若∠1=110°,则α=________.
16.【2023·汕头翠英中学模拟】如图,已知菱形OABC的顶点O(0,0),B(2,2),若菱形绕点O逆时针旋转,每秒旋转45°,则第2 023秒时,菱形的对角线交点D的坐标为________.
17.【2023·中山一中月考】如图,在平面直角坐标系中,Rt△OAB的顶点A(-2,4)在抛物线y=ax2上,直角顶点B在x轴上.将Rt△OAB绕点O顺时针旋转90°得到△OCD,边CD与该抛物线交于点P,则CP的长为__________.
18.【2022·潍坊】如图,在直角坐标系中,边长为2个单位长度的正方形ABCO绕原点O逆时针旋转75°,再沿y轴向上平移1个单位长度,则点B″的坐标为__________.
三、解答题(19,22题每题12分,20,21题每题8分,其余每题13分,共66分)
19.在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
(1)将△ABC沿x轴方向向左平移6个单位长度,画出平移后得到的△A1B1C1;
(2)将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2,并直接写出点B2,C2的坐标.
INCLUDEPICTURE"ZKJT56.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\ZKJT56.tif" \* MERGEFORMATINET
20.如图,在直角坐标平面内,Rt△AOB中,点A(1,0),OB=2,将△AOB绕点A顺时针旋转90°后与△ACD重合,点O,B分别与点C,D对应,求点D的坐标.
INCLUDEPICTURE"APP26.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\APP26.tif" \* MERGEFORMATINET
21.【母题:教材P70习题T4】平面直角坐标系第二象限内的点P(x2+2x,3)与另一点Q(x+2,y)关于原点对称,试求x+2y的值.
22.如图,在△ABC中,点D在AB边上,CB=CD,将边CA绕点C旋转到CE的位置,使得∠ECA=∠DCB,连接DE与AC交于点F,且∠B=70°,∠A=10°.
(1)求证:AB=ED;
(2)求∠AFE的度数.
INCLUDEPICTURE"DV54.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\DV54.tif" \* MERGEFORMATINET
23.【2023·北京顺义牛山二中模拟】在平面直角坐标系xOy中,已知点A(-2,2),点B(-3,-2).
(1)如果四边形ABCD是以原点O为对称中心的平行四边形,直接写出点C,D的坐标;
(2)记横、纵坐标都为整数的点叫做整点.
①写出(1)中的平行四边形ABCD内部(不包括边界)的整点的个数;
②已知平行四边形ABMN的对称中心在x轴上,且点M、点N分别在点B,A的右侧,当平行四边形ABMN内部(不包括边界)的整点的个数恰好为9个时,设直线MN的解析式为y=kx+b,求k的值及b的取值范围.
INCLUDEPICTURE"CO87.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\CO87.tif" \* MERGEFORMATINET
24.【2022·西安自弘中学期末】某数学兴趣小组在一次综合与实践活动中探究这样一个问题:将足够大的直角三角尺PEF(∠P=90°,∠F=30°)的顶点P放在等腰直角三角形ABC的斜边AC的中点O处,S△ABC=4.
(1)尝试探究:如图①,三角尺PEF的两条直角边分别与△ABC中边AB,BC交于点M,N,当PE⊥AB时:
①PM________PN(填“>”“<”或“=”);
②三角尺PEF与△ABC重叠部分的面积为________.
(2)操作发现:如图②,将三角尺PEF绕点O旋转,PM与PN相等吗?请说明理由.
(3)类比应用:如图②,在旋转过程中,三角尺PEF的两条直角边分别与△ABC中边AB,BC交于点M,N(点M不与点A,B重合),三角尺PEF与△ABC重叠部分的面积变化吗?若变化,请说明理由;若不变,请求出重叠部分的面积.
INCLUDEPICTURE"CO88.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\CO88.tif" \* MERGEFORMATINET
答案
一、1.A 2.B 3.C 4.C 5.C 6.A 7.C 8.D 9.A
10.B 点拨:∵点A(4,2),点P(0,2),
∴PA⊥y轴,PA=4.
由题意得∠APB=60°,AP=PB=4.
INCLUDEPICTURE"1A83A.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\1A83A.tif" \* MERGEFORMATINET
如图,过点B作BC⊥y轴于点C,
易知∠BPC=30°.
∴BC=2,
∴PC=2.
∴B(2,2+2).
设直线PB对应的函数解析式为y=kx+b,
则解得
∴直线PB对应的函数解析式为y=x+2.
当y=0时,x+2=0,即x=-,
∴M1不在直线PB上;
当x=-时,y=-3+2=-1,
∴M2(-,-1)在直线PB上;
当x=1时,y=+2,
∴M3(1,4)不在直线PB上;
当x=2时,y=2+2,
∴M4不在直线PB上.
二、11.(-1,5) 12.60° 13.π 14.12 15.20°
16.(,0)
点拨:∵菱形OABC的顶点O(0,0),B(2,2),∴D(1,1).∴OD=.
∵每秒旋转45°,则第2 023秒时,得45°×2 023=91 035°,91 035°÷360°=252(周),∴OD旋转了252周,
故此时菱形的对角线交点D的坐标为(,0).
17.4- 点拨:把点A(-2,4)的坐标代入y=ax2得4a=4,解得a=1,
∴抛物线的解析式为y=x2.
∵A的坐标为(-2,4),AB⊥x轴,
∴AB=4,OB=2.
∵Rt△OAB绕点O顺时针旋转90°得到△OCD,
∴OD=OB=2,∠ODC=∠OBA=90°,
∴D点坐标为(0,2),CD⊥y轴,
∴P点的纵坐标为2,把y=2代入y=x2得x2=2,解得x=±(负值舍去),
∴P点坐标为(,2),∴PD=,∴PC=CD-PD=4-.
18.(-,+1)
点拨:过点B′作B′D⊥y轴于点D,连接OB,OB′,如图所示.
INCLUDEPICTURE"1A81A.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\1A81A.tif" \* MERGEFORMATINET
由题意得,∠BOB′=75°,∠BOC=45°,OB=OB′=2.
∴∠B′OD=30°.∴B′D=OB′=.
∴OD==.
∴B′(-,).∴B″(-,+1).
三、19.解:(1)如图,△A1B1C1即为所求.
INCLUDEPICTURE"ZKJT57.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\ZKJT57.tif" \* MERGEFORMATINET
(2)如图,△AB2C2即为所求.
点B2的坐标为(4,-2),点C2的坐标为(1,-3).
20.解:∵点A(1,0),∴AO=1.
∵△AOB绕点A顺时针旋转90°后与△ACD重合,
∴AC=AO=1,CD=BO=2,CD∥x轴,AC⊥x轴.
∴点D的横坐标为1+2=3,纵坐标为1.
∴点D的坐标为(3,1).
21.解:由题意得(x2+2x)+(x+2)=0,y=-3.
解得x1=-1,x2=-2.
∵点P在第二象限,∴x2+2x<0.∴x=-1.∴x+2y=-7.
22.(1)证明:∵∠ECA=∠DCB,
∴∠ECA+∠ACD=∠DCB+∠ACD,
即∠ECD=∠BCA.由旋转可得CA=CE.
在△BCA和△DCE中,CB=CD,∠BCA=∠DCE,CA=CE,
∴△BCA≌△DCE(SAS).∴AB=ED.
(2)解:∵△BCA≌△DCE,∴∠CDE=∠B=70°.
∵CB=CD,∴∠B=∠CDB=70°.
∴∠EDA=180°-∠BDE=180°-70°×2=40°.
∴∠AFE=∠EDA+∠A=40°+10°=50°.
23.解:(1)如图,C(2,-2),D(3,2).
INCLUDEPICTURE"CO87DA.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\CO87DA.tif" \* MERGEFORMATINET
(2)①如图所示,平行四边形ABCD内部的整点有15个.
②设直线AB的解析式为y=mx+n,
∴解得
∴直线AB的解析式为y=4x+10.
依题意可知MN∥AB,∴k=4.
如图①,当直线MN过点(0,-1)时,平行四边形ABMN内部有8个整点,此时b=-1;
INCLUDEPICTURE"CO87DA2.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\CO87DA2.tif" \* MERGEFORMATINET
如图②,当直线MN过点(1,1)时,平行四边形ABMN内部有9个整点,
此时1=4+b,即b=-3.
综上,-3≤b<-1.
24.解:(1)①= ②2
(2)操作发现:将三角尺PEF绕点O旋转,PM与PN相等.理由如下:
INCLUDEPICTURE"CO88DA.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\CO88DA.tif" \* MERGEFORMATINET
如图,连接OB,∵△ABC是等腰直角三角形,O是斜边AC的中点,
∴BO⊥AC,OB=AC=OA=OC,∠ABO=∠CBO=∠ABC=45°.
∴∠AOB=90°=∠MON,∠A=∠OBN=45°.
∴∠AOB-∠BOM=∠MON-∠BOM,
即∠AOM=∠BON.
在△AOM和△BON中,
∴△AOM≌△BON(ASA).
∴OM=ON.∵P点与O点重合,∴PM=PN.
(3)类比应用:三角尺PEF与△ABC重叠部分的面积不变.理由如下:
由(2)知,OA=OC=AC,OB⊥AC,△AOM≌△BON,
∴S△AOB=S△ABC=2,S△AOM=S△BON.
∴S四边形BMPN=S△BOM+S△BON=S△BOM+S△AOM=S△AOB=2.
∴三角尺PEF与△ABC重叠部分的面积不变,重叠部分的面积为2.
一、选择题(每题3分,共30分)
1.左权县是闻名全国的民间文化艺术之乡,传统文化深沉厚重,形式丰富独特,其中小花戏、开花调、布老虎、剪纸、小会吊挂等被列为国家或省市级非物质文化遗产.下列动物剪纸作品是中心对称图形的是( )
2.【母题:教材P60例题】如图,在方格纸中,将Rt△AOB绕点B按顺时针方向旋转90°后得到Rt△A′O′B,则下列四个图形中正确的是( )
INCLUDEPICTURE"EAE66.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\EAE66.tif" \* MERGEFORMATINET INCLUDEPICTURE"EAE67.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\EAE67.tif" \* MERGEFORMATINET
3.如图,四边形ABCD为正方形,O为对角线AC,BD的交点,则△COD绕点O经过下列哪种旋转可以得到△DOA?( )
A.顺时针旋转90° B.顺时针旋转45°
C.逆时针旋转90° D.逆时针旋转45°
INCLUDEPICTURE"AB143.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\AB143.tif" \* MERGEFORMATINET INCLUDEPICTURE"S2-75.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\S2-75.tif" \* MERGEFORMATINET INCLUDEPICTURE"DV48.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\DV48.tif" \* MERGEFORMATINET INCLUDEPICTURE"QR48.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\QR48.tif" \* MERGEFORMATINET INCLUDEPICTURE"F33.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\F33.tif" \* MERGEFORMATINET
(第3题) (第4题) (第5题) (第6题) (第7题)
4.【母题:教材P77复习题T7】如图,点O是 ABCD的对称中心,EF是过点O的任意一条直线,它将平行四边形分成两部分,四边形ABOE和四边形CDOF的面积分别记为S1,S2,那么S1,S2之间的关系为( )
A. S1>S2 B. S1
5.如图,在△ABC中,∠ACB=90°,∠BAC=α,将△ABC绕点C顺时针旋转90°得到△A′B′C,点B的对应点B′在边AC上(不与点A,C重合),则∠AA′B′的度数为( )
A.α B.α-45° C.45°-α D.90°-α
6.如图,在平面直角坐标系中,把△ABC绕原点O旋转180°得到△CDA,点A,B,C的坐标分别为(-5,2),(-2,-2),(5,-2),则点D的坐标为( )
A.(2,2) B.(2,-2) C.(2,5) D.(-2,5)
7.如图,在平面直角坐标系中,△ABC绕旋转中心顺时针旋转90°后得到△A′B′C′,则其旋转中心的坐标是( )
A.(1.5,1.5) B.(1,0) C.(1,-1) D.(1.5,-0.5)
8.如图,四边形ABCD是边长为5的正方形,E是DC上一点,DE=1,将△ADE绕点A顺时针旋转到与△ABF重合,则EF=( )
A. B. C.5 D.2
INCLUDEPICTURE"XZK140.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\XZK140.tif" \* MERGEFORMATINET INCLUDEPICTURE"QR44.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\QR44.tif" \* MERGEFORMATINET INCLUDEPICTURE"1A83.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\1A83.tif" \* MERGEFORMATINET INCLUDEPICTURE"APP21.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\APP21.tif" \* MERGEFORMATINET INCLUDEPICTURE"AB289.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\AB289.tif" \* MERGEFORMATINET
(第8题) (第9题) (第10题) (第12题) (第13题)
9.如图,在平面直角坐标系中,点A,C在x轴上,点C的坐标为(-1,0),AC=2,将Rt△ABC先绕点C顺时针旋转90°,再向右平移3个单位长度,则变换后点A的对应点的坐标是( )
A.(2,2) B.(1,2) C.(-1,2) D.(2,-1)
10.【2022·杭州】如图,在平面直角坐标系中,已知点P(0,2),点A(4,2).以点P为旋转中心,把点A按逆时针方向旋转60°,得点B.在M1,M2(-,-1),M3(1,4),M4四个点中,直线PB经过的点是( )
A.M1 B.M2 C.M3 D.M4
二、填空题(每题3分,共24分)
11.【2022·云南】点A(1,-5)关于原点的对称点为点B,则点B的坐标为________.
12.如图所示的雪花图案围绕旋转中心至少旋转________后可以完全重合.
13.如图,大圆的面积为4π,大圆的两条直径互相垂直,则图中阴影部分的面积的和为________.
14.如图是一个中心对称图形,A为对称中心,若∠C=90°,∠B=30°,AC=3,则BB′的长为________.
INCLUDEPICTURE"X163a.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\X163a.tif" \* MERGEFORMATINET INCLUDEPICTURE"X163.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\X163.tif" \* MERGEFORMATINET INCLUDEPICTURE"CO85.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\CO85.tif" \* MERGEFORMATINET INCLUDEPICTURE"CO86.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\CO86.tif" \* MERGEFORMATINET INCLUDEPICTURE"1A81.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\1A81.tif" \* MERGEFORMATINET
(第14题) (第15题) (第16题) (第17题) (第18题)
15.如图,将矩形ABCD绕点A顺时针旋转到矩形AB′C′D′的位置,旋转角为α(0°<α<90°).若∠1=110°,则α=________.
16.【2023·汕头翠英中学模拟】如图,已知菱形OABC的顶点O(0,0),B(2,2),若菱形绕点O逆时针旋转,每秒旋转45°,则第2 023秒时,菱形的对角线交点D的坐标为________.
17.【2023·中山一中月考】如图,在平面直角坐标系中,Rt△OAB的顶点A(-2,4)在抛物线y=ax2上,直角顶点B在x轴上.将Rt△OAB绕点O顺时针旋转90°得到△OCD,边CD与该抛物线交于点P,则CP的长为__________.
18.【2022·潍坊】如图,在直角坐标系中,边长为2个单位长度的正方形ABCO绕原点O逆时针旋转75°,再沿y轴向上平移1个单位长度,则点B″的坐标为__________.
三、解答题(19,22题每题12分,20,21题每题8分,其余每题13分,共66分)
19.在平面直角坐标系中,△ABC的位置如图所示(每个小方格都是边长为1个单位长度的正方形).
(1)将△ABC沿x轴方向向左平移6个单位长度,画出平移后得到的△A1B1C1;
(2)将△ABC绕着点A顺时针旋转90°,画出旋转后得到的△AB2C2,并直接写出点B2,C2的坐标.
INCLUDEPICTURE"ZKJT56.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\ZKJT56.tif" \* MERGEFORMATINET
20.如图,在直角坐标平面内,Rt△AOB中,点A(1,0),OB=2,将△AOB绕点A顺时针旋转90°后与△ACD重合,点O,B分别与点C,D对应,求点D的坐标.
INCLUDEPICTURE"APP26.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\APP26.tif" \* MERGEFORMATINET
21.【母题:教材P70习题T4】平面直角坐标系第二象限内的点P(x2+2x,3)与另一点Q(x+2,y)关于原点对称,试求x+2y的值.
22.如图,在△ABC中,点D在AB边上,CB=CD,将边CA绕点C旋转到CE的位置,使得∠ECA=∠DCB,连接DE与AC交于点F,且∠B=70°,∠A=10°.
(1)求证:AB=ED;
(2)求∠AFE的度数.
INCLUDEPICTURE"DV54.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\DV54.tif" \* MERGEFORMATINET
23.【2023·北京顺义牛山二中模拟】在平面直角坐标系xOy中,已知点A(-2,2),点B(-3,-2).
(1)如果四边形ABCD是以原点O为对称中心的平行四边形,直接写出点C,D的坐标;
(2)记横、纵坐标都为整数的点叫做整点.
①写出(1)中的平行四边形ABCD内部(不包括边界)的整点的个数;
②已知平行四边形ABMN的对称中心在x轴上,且点M、点N分别在点B,A的右侧,当平行四边形ABMN内部(不包括边界)的整点的个数恰好为9个时,设直线MN的解析式为y=kx+b,求k的值及b的取值范围.
INCLUDEPICTURE"CO87.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\CO87.tif" \* MERGEFORMATINET
24.【2022·西安自弘中学期末】某数学兴趣小组在一次综合与实践活动中探究这样一个问题:将足够大的直角三角尺PEF(∠P=90°,∠F=30°)的顶点P放在等腰直角三角形ABC的斜边AC的中点O处,S△ABC=4.
(1)尝试探究:如图①,三角尺PEF的两条直角边分别与△ABC中边AB,BC交于点M,N,当PE⊥AB时:
①PM________PN(填“>”“<”或“=”);
②三角尺PEF与△ABC重叠部分的面积为________.
(2)操作发现:如图②,将三角尺PEF绕点O旋转,PM与PN相等吗?请说明理由.
(3)类比应用:如图②,在旋转过程中,三角尺PEF的两条直角边分别与△ABC中边AB,BC交于点M,N(点M不与点A,B重合),三角尺PEF与△ABC重叠部分的面积变化吗?若变化,请说明理由;若不变,请求出重叠部分的面积.
INCLUDEPICTURE"CO88.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\CO88.tif" \* MERGEFORMATINET
答案
一、1.A 2.B 3.C 4.C 5.C 6.A 7.C 8.D 9.A
10.B 点拨:∵点A(4,2),点P(0,2),
∴PA⊥y轴,PA=4.
由题意得∠APB=60°,AP=PB=4.
INCLUDEPICTURE"1A83A.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\1A83A.tif" \* MERGEFORMATINET
如图,过点B作BC⊥y轴于点C,
易知∠BPC=30°.
∴BC=2,
∴PC=2.
∴B(2,2+2).
设直线PB对应的函数解析式为y=kx+b,
则解得
∴直线PB对应的函数解析式为y=x+2.
当y=0时,x+2=0,即x=-,
∴M1不在直线PB上;
当x=-时,y=-3+2=-1,
∴M2(-,-1)在直线PB上;
当x=1时,y=+2,
∴M3(1,4)不在直线PB上;
当x=2时,y=2+2,
∴M4不在直线PB上.
二、11.(-1,5) 12.60° 13.π 14.12 15.20°
16.(,0)
点拨:∵菱形OABC的顶点O(0,0),B(2,2),∴D(1,1).∴OD=.
∵每秒旋转45°,则第2 023秒时,得45°×2 023=91 035°,91 035°÷360°=252(周),∴OD旋转了252周,
故此时菱形的对角线交点D的坐标为(,0).
17.4- 点拨:把点A(-2,4)的坐标代入y=ax2得4a=4,解得a=1,
∴抛物线的解析式为y=x2.
∵A的坐标为(-2,4),AB⊥x轴,
∴AB=4,OB=2.
∵Rt△OAB绕点O顺时针旋转90°得到△OCD,
∴OD=OB=2,∠ODC=∠OBA=90°,
∴D点坐标为(0,2),CD⊥y轴,
∴P点的纵坐标为2,把y=2代入y=x2得x2=2,解得x=±(负值舍去),
∴P点坐标为(,2),∴PD=,∴PC=CD-PD=4-.
18.(-,+1)
点拨:过点B′作B′D⊥y轴于点D,连接OB,OB′,如图所示.
INCLUDEPICTURE"1A81A.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\1A81A.tif" \* MERGEFORMATINET
由题意得,∠BOB′=75°,∠BOC=45°,OB=OB′=2.
∴∠B′OD=30°.∴B′D=OB′=.
∴OD==.
∴B′(-,).∴B″(-,+1).
三、19.解:(1)如图,△A1B1C1即为所求.
INCLUDEPICTURE"ZKJT57.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\ZKJT57.tif" \* MERGEFORMATINET
(2)如图,△AB2C2即为所求.
点B2的坐标为(4,-2),点C2的坐标为(1,-3).
20.解:∵点A(1,0),∴AO=1.
∵△AOB绕点A顺时针旋转90°后与△ACD重合,
∴AC=AO=1,CD=BO=2,CD∥x轴,AC⊥x轴.
∴点D的横坐标为1+2=3,纵坐标为1.
∴点D的坐标为(3,1).
21.解:由题意得(x2+2x)+(x+2)=0,y=-3.
解得x1=-1,x2=-2.
∵点P在第二象限,∴x2+2x<0.∴x=-1.∴x+2y=-7.
22.(1)证明:∵∠ECA=∠DCB,
∴∠ECA+∠ACD=∠DCB+∠ACD,
即∠ECD=∠BCA.由旋转可得CA=CE.
在△BCA和△DCE中,CB=CD,∠BCA=∠DCE,CA=CE,
∴△BCA≌△DCE(SAS).∴AB=ED.
(2)解:∵△BCA≌△DCE,∴∠CDE=∠B=70°.
∵CB=CD,∴∠B=∠CDB=70°.
∴∠EDA=180°-∠BDE=180°-70°×2=40°.
∴∠AFE=∠EDA+∠A=40°+10°=50°.
23.解:(1)如图,C(2,-2),D(3,2).
INCLUDEPICTURE"CO87DA.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\CO87DA.tif" \* MERGEFORMATINET
(2)①如图所示,平行四边形ABCD内部的整点有15个.
②设直线AB的解析式为y=mx+n,
∴解得
∴直线AB的解析式为y=4x+10.
依题意可知MN∥AB,∴k=4.
如图①,当直线MN过点(0,-1)时,平行四边形ABMN内部有8个整点,此时b=-1;
INCLUDEPICTURE"CO87DA2.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\CO87DA2.tif" \* MERGEFORMATINET
如图②,当直线MN过点(1,1)时,平行四边形ABMN内部有9个整点,
此时1=4+b,即b=-3.
综上,-3≤b<-1.
24.解:(1)①= ②2
(2)操作发现:将三角尺PEF绕点O旋转,PM与PN相等.理由如下:
INCLUDEPICTURE"CO88DA.tif" INCLUDEPICTURE "D:\\邵雪花\\23秋\\数学\\9RJ-全国\\word\\CO88DA.tif" \* MERGEFORMATINET
如图,连接OB,∵△ABC是等腰直角三角形,O是斜边AC的中点,
∴BO⊥AC,OB=AC=OA=OC,∠ABO=∠CBO=∠ABC=45°.
∴∠AOB=90°=∠MON,∠A=∠OBN=45°.
∴∠AOB-∠BOM=∠MON-∠BOM,
即∠AOM=∠BON.
在△AOM和△BON中,
∴△AOM≌△BON(ASA).
∴OM=ON.∵P点与O点重合,∴PM=PN.
(3)类比应用:三角尺PEF与△ABC重叠部分的面积不变.理由如下:
由(2)知,OA=OC=AC,OB⊥AC,△AOM≌△BON,
∴S△AOB=S△ABC=2,S△AOM=S△BON.
∴S四边形BMPN=S△BOM+S△BON=S△BOM+S△AOM=S△AOB=2.
∴三角尺PEF与△ABC重叠部分的面积不变,重叠部分的面积为2.
同课章节目录
