19.1.1.2 矩形的性质的运用 学案
文档属性
| 名称 | 19.1.1.2 矩形的性质的运用 学案 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-07 23:37:04 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
19.1.1.2 矩形的性质的运用 导学案
课题 19.1.1.2 矩形的性质的运用 单元 第19单元 学科 数学 年级 八年级(下)
教材分析 探索并掌握矩形的概念及其特殊的性质.在观察、操作、推理、归纳等探索过程中,掌握矩形特殊的特征与性质.
核心素养分析 在观察、操作、推理、归纳等探索过程中,发展学生的合情推理能力,进一步培养学生数学说理的习惯与能力.网
学习目标 1. 掌握矩形的特殊性质.2.会应用矩形性质解决相关问题.
重点 掌握矩形的特殊性质.
难点 应用矩形性质解决相关问题.
教学过程
课前预学 引入思考利用矩形特殊性质,我们可以解决哪些问题呢?如图,一张矩形纸片沿着对角线剪去一半,你能得到什么结论?Rt△ABC中,BO是一条怎样的线段?它的长度与斜边AC有什么关系?
新知讲解 提炼概念直角三角形一个重要的性质:直角三角形斜边上的中线等于斜边的一半。典例精讲 例1 如下图,在矩形ABCD中,AB=3,BC=4,BE⊥AC,垂足为点E.试求BE的长. 例2 如下图,在矩形ABCD中,对角线AC与BD相交于点O,AE垂直且平分线段BO,垂足为点E,BD=15cm.求AC、AB的长.
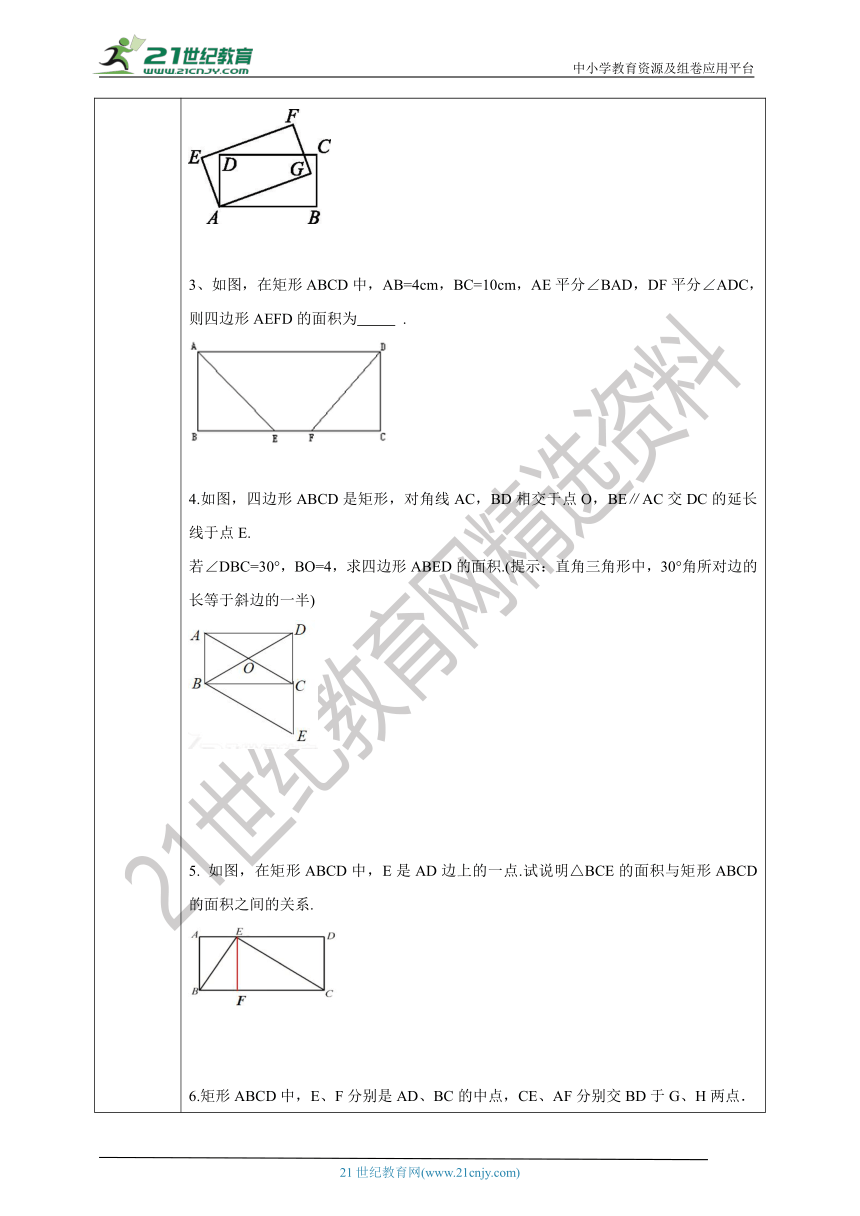
课堂练习 巩固训练1.若矩形的一条对角线与一边的夹角为40°,则两条对角线相交的锐角是 ( )A.20 ° B.40° C.80 ° D.10°2.如图,四边形ABCD和四边形AEFG都是矩形.若∠BAG=20°,则∠DAE= °.3、如图,在矩形ABCD中,AB=4cm,BC=10cm,AE平分∠BAD,DF平分∠ADC,则四边形AEFD的面积为 .4.如图,四边形ABCD是矩形,对角线AC,BD相交于点O,BE∥AC交DC的延长线于点E.若∠DBC=30°,BO=4,求四边形ABED的面积.(提示:直角三角形中,30°角所对边的长等于斜边的一半)5. 如图,在矩形ABCD中,E是AD边上的一点.试说明△BCE的面积与矩形ABCD的面积之间的关系.6.矩形ABCD中,E、F分别是AD、BC的中点,CE、AF分别交BD于G、H两点.求证:(1)四边形AFCE是平行四边形;(2)EG=FH.答案引入思考提炼概念典例精讲 例1例2 解 ∵四边形ABCD是矩形,∴ AC=BD=15(矩形对角线相等).∴ AO =1/2AC = 7.5.∵AE垂直平分BO,∴AB=AO=7.5.即AC的长为15cm,AB的长为7.5cm.巩固训练1.C2. 2024cm24.解:∵在矩形ABCD中,BO=4,∴BD=2BO=2×4=8.∵∠DBC=30°,∴CD= BD= ×8=4,∴AB=CD=4,DE=CD+CE=CD+AB=8.在Rt△BCD中,BC=∴四边形ABED的面积= ×(4+8)× = .5.解:过E作EF//AB交BC于F,∵矩形ABCD中,AD∥BC,∠A=90°又∵AB∥EF.∴四边形ABFE是矩形∴S△BEF= S四边形ABFE ,同理可证S△CEF =S四边形CDEF ∵S△BEF+S△CEF=S△BEC,SABFE+SCDEF=SABCD∴△BCE的面积是矩形ABCD的面积的一半6.证明:(1)∵四边形ABCD是矩形,∴AD∥BC,AD=BC,∵E、F分别是AD、BC的中点,∴AE=1/2AD,CF=1/2BC,∴AE=CF,∴四边形AFCE是平行四边形;(2)∵四边形AFCE是平行四边形,∴CE∥AF,∴∠DGE=∠AHD=∠BHF,∵AD∥BC,∴∠EDG=∠FBH,在△DEG和△BFH中,∴△DEG≌△BFH(AAS),∴EG=FH.
课堂小结
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
19.1.1.2 矩形的性质的运用 导学案
课题 19.1.1.2 矩形的性质的运用 单元 第19单元 学科 数学 年级 八年级(下)
教材分析 探索并掌握矩形的概念及其特殊的性质.在观察、操作、推理、归纳等探索过程中,掌握矩形特殊的特征与性质.
核心素养分析 在观察、操作、推理、归纳等探索过程中,发展学生的合情推理能力,进一步培养学生数学说理的习惯与能力.网
学习目标 1. 掌握矩形的特殊性质.2.会应用矩形性质解决相关问题.
重点 掌握矩形的特殊性质.
难点 应用矩形性质解决相关问题.
教学过程
课前预学 引入思考利用矩形特殊性质,我们可以解决哪些问题呢?如图,一张矩形纸片沿着对角线剪去一半,你能得到什么结论?Rt△ABC中,BO是一条怎样的线段?它的长度与斜边AC有什么关系?
新知讲解 提炼概念直角三角形一个重要的性质:直角三角形斜边上的中线等于斜边的一半。典例精讲 例1 如下图,在矩形ABCD中,AB=3,BC=4,BE⊥AC,垂足为点E.试求BE的长. 例2 如下图,在矩形ABCD中,对角线AC与BD相交于点O,AE垂直且平分线段BO,垂足为点E,BD=15cm.求AC、AB的长.
课堂练习 巩固训练1.若矩形的一条对角线与一边的夹角为40°,则两条对角线相交的锐角是 ( )A.20 ° B.40° C.80 ° D.10°2.如图,四边形ABCD和四边形AEFG都是矩形.若∠BAG=20°,则∠DAE= °.3、如图,在矩形ABCD中,AB=4cm,BC=10cm,AE平分∠BAD,DF平分∠ADC,则四边形AEFD的面积为 .4.如图,四边形ABCD是矩形,对角线AC,BD相交于点O,BE∥AC交DC的延长线于点E.若∠DBC=30°,BO=4,求四边形ABED的面积.(提示:直角三角形中,30°角所对边的长等于斜边的一半)5. 如图,在矩形ABCD中,E是AD边上的一点.试说明△BCE的面积与矩形ABCD的面积之间的关系.6.矩形ABCD中,E、F分别是AD、BC的中点,CE、AF分别交BD于G、H两点.求证:(1)四边形AFCE是平行四边形;(2)EG=FH.答案引入思考提炼概念典例精讲 例1例2 解 ∵四边形ABCD是矩形,∴ AC=BD=15(矩形对角线相等).∴ AO =1/2AC = 7.5.∵AE垂直平分BO,∴AB=AO=7.5.即AC的长为15cm,AB的长为7.5cm.巩固训练1.C2. 2024cm24.解:∵在矩形ABCD中,BO=4,∴BD=2BO=2×4=8.∵∠DBC=30°,∴CD= BD= ×8=4,∴AB=CD=4,DE=CD+CE=CD+AB=8.在Rt△BCD中,BC=∴四边形ABED的面积= ×(4+8)× = .5.解:过E作EF//AB交BC于F,∵矩形ABCD中,AD∥BC,∠A=90°又∵AB∥EF.∴四边形ABFE是矩形∴S△BEF= S四边形ABFE ,同理可证S△CEF =S四边形CDEF ∵S△BEF+S△CEF=S△BEC,SABFE+SCDEF=SABCD∴△BCE的面积是矩形ABCD的面积的一半6.证明:(1)∵四边形ABCD是矩形,∴AD∥BC,AD=BC,∵E、F分别是AD、BC的中点,∴AE=1/2AD,CF=1/2BC,∴AE=CF,∴四边形AFCE是平行四边形;(2)∵四边形AFCE是平行四边形,∴CE∥AF,∴∠DGE=∠AHD=∠BHF,∵AD∥BC,∴∠EDG=∠FBH,在△DEG和△BFH中,∴△DEG≌△BFH(AAS),∴EG=FH.
课堂小结
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 21世纪教育网(www.21cnjy.com)
