19.1.1.2 矩形的性质的运用 课件(共19张PPT)
文档属性
| 名称 | 19.1.1.2 矩形的性质的运用 课件(共19张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2023-03-07 22:56:14 | ||
图片预览





文档简介
(共19张PPT)
19.1.1.2 矩形的性质的运用
华师大版 八年级 下册
教学目标
教学目标:1. 掌握矩形特殊的性质.
2.会应用矩形性质解决相关问题.
教学重点:掌握矩形的特殊性质.
教学难点:应用矩形性质解决相关问题.
新知导入
情境引入
┒
邻边:
四个角都是直角
互相平分 AO=CO; BO=DO
(1)边:
(2)角:
(3)对角线:
对边:
(共性)
(共性)
(个性)
(个性)
(个性)
(共性)
A
B
C
D
O
平行 AD∥BC; AB∥ CD
相等 AB=CD; AD=BC
相 等 AC=BD
互相垂直 AB⊥BC; AB ⊥ AD
A
B
D
C
O
∠BAD=∠ABC=∠BCD=∠CDA= 90°
┒
┒
┒
OA=OB=OC=OD=相等的对角线的一半
对角相等、邻角互补
(共性)
矩形的性质
新知讲解
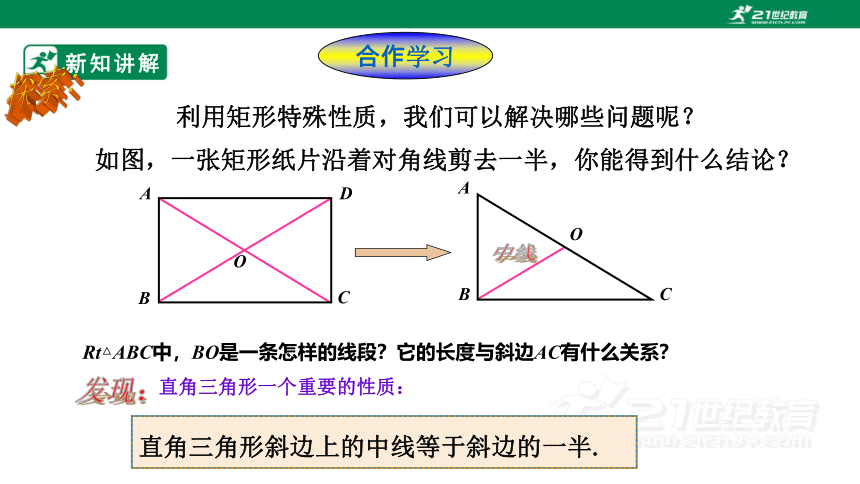
合作学习
利用矩形特殊性质,我们可以解决哪些问题呢?
如图,一张矩形纸片沿着对角线剪去一半,你能得到什么结论?
发现:
探索:
直角三角形一个重要的性质:
A
B
C
D
O
B
C
O
A
Rt△ABC中,BO是一条怎样的线段?它的长度与斜边AC有什么关系?
中线
直角三角形斜边上的中线等于斜边的一半.
提炼概念
这个性质是矩形所特有的哟!
直角三角形斜边上的中线等于斜边的一半.
温馨提示:
几何语言
直角三角形的性质
如图,Rt△ABC中,∠ACB=90。,BO是斜边AB的中线.
B
C
O
A
∵在Rt△ABC中, BO是斜边AC上的中线
∴
典例精讲
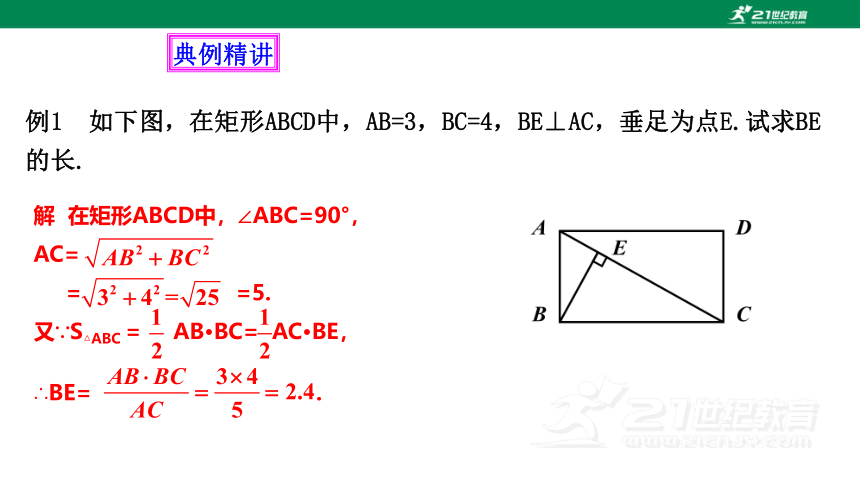
例1 如下图,在矩形ABCD中,AB=3,BC=4,BE⊥AC,垂足为点E.试求BE的长.
解 在矩形ABCD中,∠ABC=90°,
AC=
= =5.
又∵S△ABC = AB·BC= AC·BE,
∴BE= .
例2 如下图,在矩形ABCD中,对角线AC与BD相交于点O,AE垂直且平分线段BO,垂足为点E,BD=15cm.求AC、AB的长.
归纳概念
解题指导:矩形问题 直角三角形或等腰三角形
连接对角线
转化
课堂练习
1.若矩形的一条对角线与一边的夹角为40°,则两条对角线相交的锐角是 ( )
A.20 ° B.40° C.80 ° D.10°
C
2.如图,四边形ABCD和四边形AEFG都是矩形.若∠BAG=20°,则
∠DAE= °.
3.如图,在矩形ABCD中,AB=4cm,BC=10cm,AE平分∠BAD,DF平分∠ADC,则四边形AEFD的面积为 .
20
24cm2
4.如图,四边形ABCD是矩形,对角线AC,BD相交于点O,BE∥AC交DC的延长线于点E.
若∠DBC=30°,BO=4,求四边形ABED的面积.(提示:直角三角形中,30°角所对边的长等于斜边的一半)
A
B
C
D
O
E
解:∵在矩形ABCD中,BO=4,∴BD=2BO=2×4=8.
∵∠DBC=30°,∴CD= BD= ×8=4,
∴AB=CD=4,DE=CD+CE=CD+AB=8.
在Rt△BCD中,BC=
∴四边形ABED的面积= ×(4+8)× = .
5. 如图,在矩形ABCD中,E是AD边上的一点.试说明△BCE的面积与矩形ABCD的面积之间的关系.
解:过E作EF//AB交BC于F,
∵矩形ABCD中,AD∥BC,∠A=90°
又∵AB∥EF.∴四边形ABFE是矩形
∴S△BEF= S四边形ABFE ,同理可证S△CEF = S四边形CDEF ∵S△BEF+S△CEF=S△BEC,SABFE+SCDEF=SABCD
∴△BCE的面积是矩形ABCD的面积的一半
F
6.矩形ABCD中,E、F分别是AD、BC的中点,CE、AF分别交BD于G、H两点.
求证:(1)四边形AFCE是平行四边形;(2)EG=FH.
证明:(1)∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,
∵E、F分别是AD、BC的中点,
∴AE=AD,CF=BC,
∴AE=CF,
∴四边形AFCE是平行四边形;
(2)∵四边形AFCE是平行四边形,
∴CE∥AF,
∴∠DGE=∠AHD=∠BHF,
∵AD∥BC,
∴∠EDG=∠FBH,
在△DEG和△BFH中,
∴△DEG≌△BFH(AAS),
∴EG=FH.
课堂总结
矩形性质的
应用
矩形的性质与垂直综合
矩形的性质与勾股定理综合
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
19.1.1.2 矩形的性质的运用
华师大版 八年级 下册
教学目标
教学目标:1. 掌握矩形特殊的性质.
2.会应用矩形性质解决相关问题.
教学重点:掌握矩形的特殊性质.
教学难点:应用矩形性质解决相关问题.
新知导入
情境引入
┒
邻边:
四个角都是直角
互相平分 AO=CO; BO=DO
(1)边:
(2)角:
(3)对角线:
对边:
(共性)
(共性)
(个性)
(个性)
(个性)
(共性)
A
B
C
D
O
平行 AD∥BC; AB∥ CD
相等 AB=CD; AD=BC
相 等 AC=BD
互相垂直 AB⊥BC; AB ⊥ AD
A
B
D
C
O
∠BAD=∠ABC=∠BCD=∠CDA= 90°
┒
┒
┒
OA=OB=OC=OD=相等的对角线的一半
对角相等、邻角互补
(共性)
矩形的性质
新知讲解
合作学习
利用矩形特殊性质,我们可以解决哪些问题呢?
如图,一张矩形纸片沿着对角线剪去一半,你能得到什么结论?
发现:
探索:
直角三角形一个重要的性质:
A
B
C
D
O
B
C
O
A
Rt△ABC中,BO是一条怎样的线段?它的长度与斜边AC有什么关系?
中线
直角三角形斜边上的中线等于斜边的一半.
提炼概念
这个性质是矩形所特有的哟!
直角三角形斜边上的中线等于斜边的一半.
温馨提示:
几何语言
直角三角形的性质
如图,Rt△ABC中,∠ACB=90。,BO是斜边AB的中线.
B
C
O
A
∵在Rt△ABC中, BO是斜边AC上的中线
∴
典例精讲
例1 如下图,在矩形ABCD中,AB=3,BC=4,BE⊥AC,垂足为点E.试求BE的长.
解 在矩形ABCD中,∠ABC=90°,
AC=
= =5.
又∵S△ABC = AB·BC= AC·BE,
∴BE= .
例2 如下图,在矩形ABCD中,对角线AC与BD相交于点O,AE垂直且平分线段BO,垂足为点E,BD=15cm.求AC、AB的长.
归纳概念
解题指导:矩形问题 直角三角形或等腰三角形
连接对角线
转化
课堂练习
1.若矩形的一条对角线与一边的夹角为40°,则两条对角线相交的锐角是 ( )
A.20 ° B.40° C.80 ° D.10°
C
2.如图,四边形ABCD和四边形AEFG都是矩形.若∠BAG=20°,则
∠DAE= °.
3.如图,在矩形ABCD中,AB=4cm,BC=10cm,AE平分∠BAD,DF平分∠ADC,则四边形AEFD的面积为 .
20
24cm2
4.如图,四边形ABCD是矩形,对角线AC,BD相交于点O,BE∥AC交DC的延长线于点E.
若∠DBC=30°,BO=4,求四边形ABED的面积.(提示:直角三角形中,30°角所对边的长等于斜边的一半)
A
B
C
D
O
E
解:∵在矩形ABCD中,BO=4,∴BD=2BO=2×4=8.
∵∠DBC=30°,∴CD= BD= ×8=4,
∴AB=CD=4,DE=CD+CE=CD+AB=8.
在Rt△BCD中,BC=
∴四边形ABED的面积= ×(4+8)× = .
5. 如图,在矩形ABCD中,E是AD边上的一点.试说明△BCE的面积与矩形ABCD的面积之间的关系.
解:过E作EF//AB交BC于F,
∵矩形ABCD中,AD∥BC,∠A=90°
又∵AB∥EF.∴四边形ABFE是矩形
∴S△BEF= S四边形ABFE ,同理可证S△CEF = S四边形CDEF ∵S△BEF+S△CEF=S△BEC,SABFE+SCDEF=SABCD
∴△BCE的面积是矩形ABCD的面积的一半
F
6.矩形ABCD中,E、F分别是AD、BC的中点,CE、AF分别交BD于G、H两点.
求证:(1)四边形AFCE是平行四边形;(2)EG=FH.
证明:(1)∵四边形ABCD是矩形,
∴AD∥BC,AD=BC,
∵E、F分别是AD、BC的中点,
∴AE=AD,CF=BC,
∴AE=CF,
∴四边形AFCE是平行四边形;
(2)∵四边形AFCE是平行四边形,
∴CE∥AF,
∴∠DGE=∠AHD=∠BHF,
∵AD∥BC,
∴∠EDG=∠FBH,
在△DEG和△BFH中,
∴△DEG≌△BFH(AAS),
∴EG=FH.
课堂总结
矩形性质的
应用
矩形的性质与垂直综合
矩形的性质与勾股定理综合
作业布置
教材课后配套作业题。
谢谢
21世纪教育网(www.21cnjy.com)
中小学教育资源网站
兼职招聘:
https://www.21cnjy.com/recruitment/home/admin
