数学 2014届中考二轮复习真题演练(含答案解析)
文档属性
| 名称 | 数学 2014届中考二轮复习真题演练(含答案解析) | 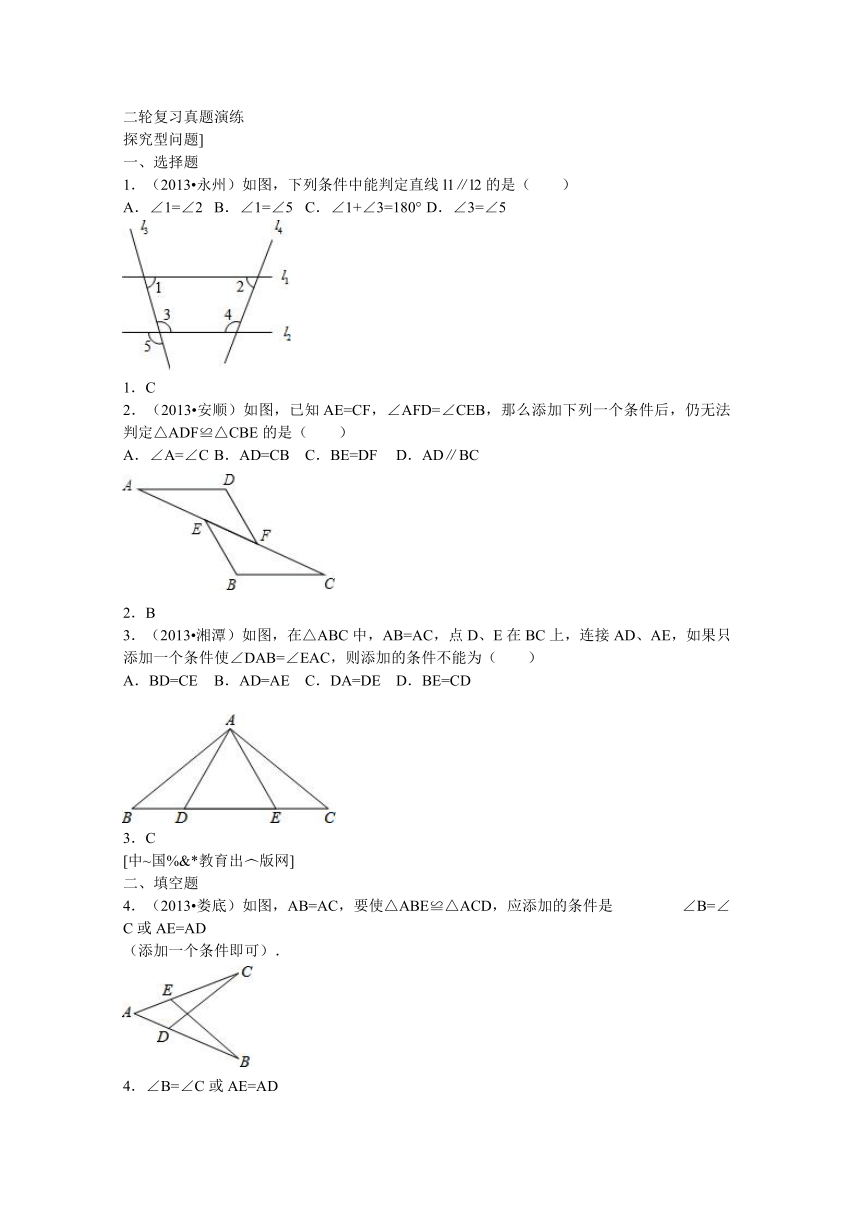 | |
| 格式 | zip | ||
| 文件大小 | 321.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2014-04-16 08:34:59 | ||
图片预览





文档简介
二轮复习真题演练
探究型问题]
一、选择题
1.(2013 永州)如图,下列条件中能判定直线l1∥l2的是( )
A.∠1=∠2 B.∠1=∠5 C.∠1+∠3=180° D.∠3=∠5
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201307/21/f7dcb4b9.png" \* MERGEFORMATINET
1.C
2.(2013 安顺)如图,已知AE=CF,∠AFD=∠CEB,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是( )
A.∠A=∠C B.AD=CB C.BE=DF D.AD∥BC
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201306/98/d86a75c5.png" \* MERGEFORMATINET
2.B
3.(2013 湘潭)如图,在△ABC中 ( http: / / www.21cnjy.com ),AB=AC,点D、E在BC上,连接AD、AE,如果只添加一个条件使∠DAB=∠EAC,则添加的条件不能为( )
A.BD=CE B.AD=AE C.DA=DE D.BE=CD
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201307/10/810af566.png" \* MERGEFORMATINET
3.C
[中~国%&*教育出︿版网]
二、填空题
4.(2013 娄底)如图,AB=AC,要使△ABE≌△ACD,应添加的条件是 ∠B=∠C或AE=AD
(添加一个条件即可).
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201307/24/577f9285.png" \* MERGEFORMATINET
4.∠B=∠C或AE=AD
5.(2013 白银)如图,已知BC=EC,∠BCE=∠ACD,要使△ABC≌△DEC,则应添加的一个条件为 AC=CD
.(答案不唯一,只需填一个)[来~源:中国教育出版%&网︿#]
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201306/106/54af345d.png" \* MERGEFORMATINET
5.AC=CD
6.(2013 上海)如图,在△ABC和△DEF中,点B、F、C、E在同一直线上,BF=CE,AC∥DF,请添加一个条件,使△ABC≌△DEF,这个添加的条件可以是 AC=DF
.(只需写一个,不添加辅助线)
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201306/71/6c44a2d9.png" \* MERGEFORMATINET
6.AC=DF
7.(2013 黑龙江)如图所示,平行四边形ABCD的对角线AC、BD相交于点O,试添加一个条件: AD=DC
,使得平行四边形ABCD为菱形.
7.AD=DC
8.(2013 西城区一模)在平面直角坐标系xOy中,有一只电子青蛙在点A(1,0)处.
第一次,它从点A先向右跳跃1个单位,再向上跳跃1个单位到达点A1;
第二次,它从点A1先向左跳跃2个单位,再向下跳跃2个单位到达点A2;
第三次,它从点A2先向右跳跃3个单位,再向上跳跃3个单位到达点A3;
第四次,它从点A3先向左跳跃4个单位,再向下跳跃4个单位到达点A4;
依此规律进行,点A6的坐标为 (-2-3)
;若点An的坐标为(2013,2012),则n= 4023
.[中
8.(-2-3),4023
9.(2013 湛江)如图,所有正三角形的一边平行于x轴,一顶点在y轴上.从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1、A2、A3、A4…表示,其中A1A2与x轴、底边A1A2与A4A5、A4A5与A7A8、…均相距一个单位,则顶点A3的坐标是 -1)
,A92的坐标是 (31,-31)
.
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201306/68/370e22ea.png" \* MERGEFORMATINET
9.(0, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ),(31,-31)
10.(2013 绍兴)如图钢架中,焊上等 ( http: / / www.21cnjy.com )长的13根钢条来加固钢架,若AP1=P1P2=P2P3=…=P13P14=P14A,则∠A的度数是 12°
.
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201307/44/114660b3.png" \* MERGEFORMATINET
10.12°
三、解答题
11.(2013 茂名)如图,在 ABCD中,点E是AB边的中点,DE与CB的延长线交于点F.[来
(1)求证:△ADE≌△BFE;
(2)若DF平分∠ADC,连接CE.试判断CE和DF的位置关系,并说明理由.
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201307/65/f0800fb5.png" \* MERGEFORMATINET
11.解:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC.
又∵点F在CB的延长线上,
∴AD∥CF,
∴∠1=∠2.
∵点E是AB边的中点,
∴AE=BE.
∵在△ADE与△BFE中,
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,21世纪教育网
∴△ADE≌△BFE(AAS);
(2)解:CE⊥DF.理由如下:
如图,连接CE.
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201307/76/d0fc22bc.png" \* MERGEFORMATINET
由(1)知,△ADE≌△BFE,
∴DE=FE,即点E是DF的中点,∠1=∠2.
∵DF平分∠ADC,
∴∠1=∠3,
∴∠3=∠2,
∴CD=CF,
∴CE⊥DF.
12.(2013 白银)如图,在△ABC ( http: / / www.21cnjy.com )中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)BD与CD有什么数量关系,并说明理由;
(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201208/30/b8538211.png" \* MERGEFORMATINET
12.解:(1)BD=CD.
理由如下:∵AF∥BC,
∴∠AFE=∠DCE,
∵E是AD的中点,
∴AE=DE,
在△AEF和△DEC中, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
∴△AEF≌△DEC(AAS),
∴AF=CD,
∵AF=BD,
∴BD=CD;
(2)当△ABC满足:AB=AC时,四边形AFBD是矩形.
理由如下:∵AF∥BD,AF=BD,
∴四边形AFBD是平行四边形,
∵AB=AC,BD=CD,
∴∠ADB=90°,
∴ AFBD是矩形.
13.(2013 无锡) ( http: / / www.21cnjy.com )如图,四边形ABCD中,对角线AC与BD相交于点O,在①AB∥CD;②AO=CO;③AD=BC中任意选取两个作为条件,“四边形ABCD是平行四边形”为结论构造命题.
(1)以①②作为条件构成的命题是真命题吗?若是,请证明;若不是,请举出反例;
(2)写出按题意构成的所有命题中的假命题,并举出反例加以说明.(命题请写成“如果…,那么….”的形式)
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201307/14/ad9fdcce.png" \* MERGEFORMATINET
13.(1)以①②作为条件构成的命题是真命题,
证明:∵AB∥CD,
∴△AOB∽△COD,
∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
∵AO=OC,
∴OB=OD,
∴四边形ABCD是平行四边形.
(2)根据①③作为条件构成的命题是假命题,即如果有一组对边平行,而另一组对边相等的四边形时平行四边形,如等腰梯形符合,但不是平行四边形;
根据②③作为条件构成的命题是假命题,即如果一个四边形ABCD的对角线交于O,且OA=OC,AD=BC,那么这个四边形时平行四边形,如图,
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201307/21/dbeb55f2.png" \* MERGEFORMATINET
根据已知不能推出OB=OD或AD∥BC或AB=DC,即四边形不是平行四边形.[来源:z~@z︿step.#*com]
14.(2013 宁波)已知抛物线y=ax2+bx+c与x轴交于点A(1,0),B(3,0),且过点C(0,-3).
(1)求抛物线的解析式和顶点坐标;
(2)请你写出一种平移的方法,使平移后抛物线的顶点落在直线y=-x上,并写出平移后抛物线的解析式.[中%国教*~育︿出版网@]
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "../AppData/Local/Temp/Application%20Data/360se6/User%20Data/Temp/f403c292.png" \* MERGEFORMAT
14.解:(1)∵抛物线与x轴交于点A(1,0),B(3,0),
可设抛物线解析式为y=a(x-1)(x-3),
把C(0,-3)代入得:3a=-3,
解得:a=-1,
故抛物线解析式为y=-(x-1)(x-3),
即y=-x2+4x-3,
∵y=-x2+4x-3=-(x-2)2+1,
∴顶点坐标(2,1);
(2)先向左平移2个单位,再向下平移1个单位,得到的抛物线的解析式为y=-x2,平移后抛物线的顶点为(0,0)落在直线y=-x上.
15.(2013 凉山州)先阅读以下材料,然后解答问题:
材料:将二次函数y=-x2+2x+3的图象向左平移1个单位,再向下平移2个单位,求平移后的抛物线的解析式(平移后抛物线的形状不变).
解:在抛物线y=-x2+2x+3图象上 ( http: / / www.21cnjy.com )任取两点A(0,3)、B(1,4),由题意知:点A向左平移1个单位得到A′(-1,3),再向下平移2个单位得到A″(-1,1);点B向左平移1个单位得到B′(0,4),再向下平移2个单位得到B″(0,2).
设平移后的抛物线的解析式为y=-x2+bx+c.则点A″(-1,1),B″(0,2)在抛物线上.可得:
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,解得: HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .所以平移后的抛物线的解析式为:y=-x2+2.
根据以上信息解答下列问题:
将直线y=2x-3向右平移3个单位,再向上平移1个单位,求平移后的直线的解析式.
15.解:在直线y=2x-3上任取一点A(0,-3),由题意知A向右平移3个单位,再向上平移1个单位得到A′(3,-2),
设平移后的解析式为y=2x+b,
则A′(3,-2)在y=2x+b的解析式上,
-2=2×3+b,
解得:b=-8,
所以平移后的直线的解析式为y=2x-8.
16.(2013 湖州)一节数学课后,老师布置了一道课后练习题:
如图,已知在Rt△ABC中,AB= ( http: / / www.21cnjy.com )BC,∠ABC=90°,BO⊥AC,于点O,点PD分别在AO和BC上,PB=PD,DE⊥AC于点E,求证:△BPO≌△PDE.
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201306/77/7f4b526d.png" \* MERGEFORMATINET
(1)理清思路,完成解答(2)本题证明的思路可用下列框图表示:
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201306/80/051b5901.png" \* MERGEFORMATINET
根据上述思路,请你完整地书写本题的证明过程.
(2)特殊位置,证明结论
若PB平分∠ABO,其余条件不变.求证:AP=CD.
(3)知识迁移,探索新知
若点P是一个动点,点P运动到OC的 ( http: / / www.21cnjy.com )中点P′时,满足题中条件的点D也随之在直线BC上运动到点D′,请直接写出CD′与AP′的数量关系.(不必写解答过程)
16.(1)证明:∵PB=PD,
∴∠2=∠PBD,
∵AB=BC,∠ABC=90°,
∴∠C=45°,
∵BO⊥AC,
∴∠1=45°,
∴∠1=∠C=45°,
∵∠3=∠PBO-∠1,∠4=∠2-∠C,
∴∠3=∠4,
∵BO⊥AC,DE⊥AC,
∴∠BOP=∠PED=90°,
在△BPO和△PDE中
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
∴△BPO≌△PDE(AAS);
(2)证明:由(1)可得:∠3=∠4,
∵BP平分∠ABO,
∴∠ABP=∠3,
∴∠ABP=∠4,]
在△ABP和△CPD中
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 。
∴△ABP≌△CPD(AAS),
∴AP=CD.
(3)解:CD′与AP′的数量关系是CD′= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 AP′.
理由是:如图,
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201306/80/8ee3e1b3.png" \* MERGEFORMATINET
设OP=PC=x,则AO=OC=2x=BO,
则AP=2x+x=3x,
由(2)知BO=PE,
PE=2x,CE=2x-x=x,
∵∠E=90°,∠ECD=∠ACB=45°,
∴DE=x,由勾股定理得:CD= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 x,
即AP=3x,CD= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 x,
∴CD′与AP′的数量关系是CD′= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 AP′
17.(2013 淄博)分别以 ABCD(∠CDA≠90°)的三边AB,CD,DA为斜边作等腰直角三角形,△ABE,△CDG,△ADF.
(1)如图1,当三个等腰直角三角形都在该平行四边形外部时,连接GF,EF.请判断GF与EF的关系(只写结论,不需证明);
(2)如图2,当三个等腰直角三角形都在该平行四边形内部时,连接GF,EF,(1)中结论还成立吗?若成立,给出证明;若不成立,说明理由.
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201307/46/e0cd404a.png" \* MERGEFORMATINET
17.解:(1)∵四边形ABCD是平行四边形,
∴AB=CD,∠DAB+∠ADC=180°,
∵△ABE,△CDG,△ADF都是等腰直角三角形,
∴DG=CG=AE=BE,DF=AF,∠CDG=∠ADF=∠BAE=45°,
∴∠GDF=∠GDC+∠CDA+∠ADF=90°+∠CDA,
∠EAF=360°-∠BAE-∠DAF-∠BAD=270°-(180°-∠CDA)=90°+∠CDA,[来源:21世纪教育网]
∴∠FDG=∠EAF,
∵在△EAF和△GDF中,
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
∴△EAF≌△GDF(SAS),
∴EF=FG,∠EFA=∠DFG,即∠GFD+∠GFA=∠EFA+∠GFA,
∴∠GFE=90°,
∴GF⊥EF;
(2)GF⊥EF,GF=EF成立;
理由:∵四边形ABCD是平行四边形,
∴AB=CD,∠DAB+∠ADC=180°,
∵△ABE,△CDG,△ADF都是等腰直角三角形,
∴DG=CG=AE=BE,DF=AF,∠CDG=∠ADF=∠BAE=45°,
∴∠BAE+∠FDA+∠EAF+∠ADF+∠FDC=180°,
∴∠EAF+∠CDF=45°,
∵∠CDF+∠GDF=45°,
∴∠FDG=∠EAF,
∵在△EAF和△GDF中,
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
∴△EAF≌△GDF(SAS),
∴EF=FG,∠EFA=∠DFG,即∠GFD+∠GFA=∠EFA+∠GFA,
∴∠GFE=90°,
∴GF⊥EF.
18.(2013 张家界)如图,△ABC中 ( http: / / www.21cnjy.com ),点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201306/106/555ab352.png" \* MERGEFORMATINET
18.(1)证明:如图,[
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201306/108/a031e6eb.png" \* MERGEFORMATINET
∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
∴∠2=∠5,4=∠6,
∵MN∥BC,
∴∠1=∠5,3=∠6,
∴∠1=∠2,∠3=∠4,
∴EO=CO,FO=CO,
∴OE=OF;
(2)∵∠2=∠5,∠4=∠6,
∴∠2+∠4=∠5+∠6=90°,
∵CE=12,CF=5,
∴EF= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 =13,
∴OC= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 EF=6.5;
(3)答:当点O在边AC上运动到AC中点时,四边形AECF是矩形.
证明:当O为AC的中点时,AO=CO,
∵EO=FO,
∴四边形AECF是平行四边形,
∵∠ECF=90°,
∴平行四边形AECF是矩形.
19.(2013 衡阳)如图,P为正方形ABCD的边AD上的一个动点,AE⊥BP,CF⊥BP,垂足分别为点E、F,已知AD=4.
(1)试说明AE2+CF2的值是一个常数;
(2)过点P作PM∥FC交CD于点M,点P在何位置时线段DM最长,并求出此时DM的值.
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201306/87/a011bf86.png" \* MERGEFORMATINET
19.解:(1)由已知∠AEB=∠BFC=90°,AB=BC,
又∵∠ABE+∠FBC=∠BCF+∠FBC,
∴∠ABE=∠BCF,
∵在△ABE和△BCF中,
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
∴△ABE≌△BCF(AAS),
∴AE=BF,
∴AE2+CF2=BF2+CF2=BC2=16为常数;
(2)设AP=x,则PD=4-x,
由已知∠DPM=∠PAE=∠ABP,
∴△PDM∽△BAP,
∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
即 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
∴DM= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
当x=2时,DM有最大值为1.
20.(2013 宁夏)在 ( http: / / www.21cnjy.com ) ABCD中,P是AB边上的任意一点,过P点作PE⊥AB,交AD于E,连结CE,CP.已知∠A=60°;[来%源︿#:&中教网@]
(1)若BC=8,AB=6,当AP的长为多少时,△CPE的面积最大,并求出面积的最大值.
(2)试探究当△CPE≌△CPB时, ABCD的两边AB与BC应满足什么关系?
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201307/14/f39d600c.png" \* MERGEFORMATINET [
20.解:(1)如图,延长PE交CD的延长线于F,
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201307/23/7ed9ec7e.png" \* MERGEFORMATINET
设AP=x,△CPE的面积为y,
∵四边形ABCD为平行四边形,
∴AB=DC=6,AD=BC=8,
∵Rt△APE,∠A=60°,
∴∠PEA=30°,
∴AE=2x,PE= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 x,
在Rt△DEF中,∠DEF=∠PEA=30°,DE=AD-AE=8-2x,
∴DF= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 DE=4-x,
∵AB∥CD,PF⊥AB,
∴PF⊥CD,
∴S△CPE= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 PE CF,
即y= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 × HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 x×(10-x)=- HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 x2+5 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 x,
配方得:y=- HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 (x-5)2+ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
当x=5时,y有最大值 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
即AP的长为5时,△CPE的面积最大,最大面积是 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ;
(2)当△CPE≌△CPB时,有BC=CE,∠B=∠PEC=120°,
∴∠CED=180°-∠AEP-∠PEC=30°,
∵∠ADC=120°,
∴∠ECD=∠CED=180°-120°-30°=30°,
∴DE=CD,即△EDC是等腰三角形,
过D作DM⊥CE于M,则CM= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 CE,
在Rt△CMD中,∠ECD=30°,
∴cos30°= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
∴CM= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 CD,
∴CE= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 CD,
∵BC=CE,AB=CD,
∴BC= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 AB,
则当△CPE≌△CPB时,BC与AB满足的关系为BC= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 AB.
21.(2013 南平)在矩形ABCD中,点E在BC边上,过E作EF⊥AC于F,G为线段AE的中点,连接BF、FG、GB.设 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 =k.
(1)证明:△BGF是等腰三角形;
(2)当k为何值时,△BGF是等边三角形?
(3)我们知道:在一个三角形中,等边所对的角相等;反过来,等角所对的边也相等.事实上,在一个三角形中,较大的边所对的角也较大;反之也成立.
利用上述结论,探究:当△BGF分别为锐角、直角、钝角三角形时,k的取值范围.
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201307/66/e6843b8b.png" \* MERGEFORMATINET
21.解:(1)证明:∵EF⊥AC于点F,
∴∠AFE=90°[
∵在Rt△AEF中,G为斜边AE的中点,
∴GF= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 AE,
在Rt△ABE中,同理可得BG= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 AE,
∴GF=GB,
∴△BGF为等腰三角形;
(2)当△BGF为等边三角形时,∠BGF=60°
∵GF=GB=AG,
∴∠BGE=2∠BAE,∠FGE=2∠CAE
∴∠BGF=2∠BAC,
∴∠BAC=30°,
∴∠ACB=60°,
∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 =tan∠ACB= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
∴当k= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 时,△BGF为等边三角形;
(3)由(1)得△BGF为等腰三角形,由(2)得∠BAC= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ∠BGF,
∴当△BGF为锐角三角形时,∠BGF<90°,
∴∠BAC<45°,
∴AB>BC,
∴k= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 >1;
当△BGF为直角三角形时,∠BGF=90°,
∴∠BAC=45°
∴AB=BC,
∴k= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 =1;
当△BGF为钝角三角形时,∠BGF>90°,
∴∠BAC>45°[
∴AB<BC,
∴k= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 <1;
∴0<k<1.
22.(2013 德阳) ( http: / / www.21cnjy.com )如图,已知AB是⊙O直径,BC是⊙O的弦,弦ED⊥AB于点F,交BC于点G,过点C作⊙O的切线与ED的延长线交于点P.
(1)求证:PC=PG;21世纪教育网
(2)点C在劣弧AD上运动时,其他条件不变,若点G是BC的中点,试探究CG、BF、BO三者之间的数量关系,并写出证明过程;
(3)在满足(2)的条件下,已知⊙O的半径为5,若点O到BC的距离为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 时,求弦ED的长.
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201307/67/ee1cbaa1.png" \* MERGEFORMATINET
22.(1)证明:连结OC,如图,
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201307/94/e5ce4806.png" \* MERGEFORMATINET
∵PC为⊙O的切线,
∴OC⊥PC,
∴∠OCG+∠PCG=90°,
∵ED⊥AB,
∴∠B+∠BGF=90°,
∵OB=OC,
∴∠B=∠OCG,
∴∠PCG=∠BGF,
而∠BGF=∠PGC,
∴∠PGC=∠PCG,
∴PC=PG;
(2)解:CG、BF、BO三者之间的数量关系为CG2=BO BF.理由如下:
连结OG,如图,
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201307/94/e5ce4806.png" \* MERGEFORMATINET
∵点G是BC的中点,
∴OG⊥BC,BG=CG,
∴∠OGB=90°,
∵∠OBG=∠GBF,
∴Rt△BOG∽Rt△BGF,
∴BG:BF=BO: BG,
∴BG2=BO BF,
∴CG2=BO BF;
(3)解:连结OE,如图,
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201307/94/e5ce4806.png" \* MERGEFORMATINET
由(2)得BG⊥BC,
∴OG= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
在Rt△OBG中,OB=5,
∴BG= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 =2 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
由(2)得BG2=BO BF,
∴BF= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 =4,
∴OF=1,
在Rt△OEF中,EF= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 =2 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
∵AB⊥ED,
∴EF=DF,
∴DE=2EF=4 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
23.(2013 泉州)如图1,在平面直角坐标系中,正方形OABC的顶点A(-6,0),过点E(-2,0)作EF∥AB,交BO于F;
(1)求EF的长;
(2)过点F作直线l分别与直线AO、直线BC交于点H、G;
①根据上述语句,在图1上画出图形,并证明 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ;
②过点G作直线GD∥AB,交x轴于点D,以圆O为圆心,OH长为半径在x轴上方作半圆(包括直径两端点),使它与GD有公共点P.如图2所示,当直线l绕点F旋转时,点P也随之运动,证明: HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,并通过操作、观察,直接写出BG长度的取值范围(不必说理);
(3)在(2)中,若点M(2, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ),探索2PO+PM的最小值.
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201307/106/4a47676d.png" \* MERGEFORMATINET
23.(1)解:解法一:在正方形OABC中,
∠FOE=∠BOA= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ∠COA=45°.
∵EF∥AB,
∴∠FEO=∠BAO=90°,
∴∠EFO=∠FOE=45°,
又E(-2,0),
∴EF=EO=2.
解法二:∵A(-6,0),C(0,6),E(-2,0),
∴OA=AB=6,EO=2,
∵EF∥AB,
∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,即 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
∴EF=6× HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 =2.
(2)①画图,如答图1所示:
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201307/106/23f569c0.png" \* MERGEFORMATINET
证明:∵四边形OABC是正方形,
∴OH∥BC,
∴△OFH∽△BFG,
∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ;
∵EF∥AB,
∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ;
∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
②证明:∵半圆与GD交于点P,
∴OP=OH.
由①得: HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
又EO=2,EA=OA-EO=6-2=4,
∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 = HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
通过操作、观察可得,4≤BG≤12.
(3)解:由(2)可得: HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 = HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
∴2OP+PM=BG+PM.
如答图2所示,过点M作直线MN⊥AB于点N,交GD于点K,则四边形BNKG为矩形,
∴NK=BG.
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201307/106/b151b5b7.png" \* MERGEFORMATINET
∴2OP+PM=BG+PM=NK+PM≥NK+KM,
当点P与点K重合,即当点P在直线MN上时,等号成立.
又∵NK+KM≥MN=8,
当点K在线段MN上时,等号成立.
∴当点P在线段MN上时,2OP+PM的值最小,最小值为8.
24.(2013 梅州)用如图①,②所示的两个直角三角形(部分边长及角的度数在图中已标出),完成以下两个探究问题:
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201307/112/5f1388f5.png" \* MERGEFORMATINET [来源︿:zz&step.co@~m%]
探究一:将以上两个三角形如图③拼接(BC和ED重合),在BC边上有一动点P.
(1)当点P运动到∠CFB的角平分线上时,连接AP,求线段AP的长;
(2)当点P在运动的过程中出现PA=FC时,求∠PAB的度数.21世纪教育网
探究二:如图④,将△DEF的顶点D放在 ( http: / / www.21cnjy.com )△ABC的BC边上的中点处,并以点D为旋转中心旋转△DEF,使△DEF的两直角边与△ABC的两直角边分别交于M、N两点,连接MN.在旋转△DEF的过程中,△AMN的周长是否存在有最小值?若存在,求出它的最小值;若不存在,请说明理由.
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201307/112/154e0a91.png" \* MERGEFORMATINET
24.解:探究一:(1)依题意画出图形,如答图1所示:
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201307/112/20242b76.png" \* MERGEFORMATINET
由题意,得∠CFB=60°,FP为角平分线,则∠CFP=30°,
∴CF=BC sin30°=3× HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 = HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
∴CP=CF tan∠CFP= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 × HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 =1.
过点A作AG⊥BC于点G,则AG= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 BC= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
∴PG=CG-CP= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 -1= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
在Rt△APG中,由勾股定理得:
AP= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
(2)由(1)可知,FC= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
如答图2所示,以点A为圆心,以FC= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 长为半径画弧,与BC交于点P1、P2,则AP1=AP2= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201307/112/2c9d35a5.png" \* MERGEFORMATINET [ww@w#.zzs%t~e&p.com]
过点A过AG⊥BC于点G,则AG= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 BC= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
在Rt△AGP1中,cos∠P1AG= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
∴∠P1AG=30°,[中国教#育%&@出~版网]
∴∠P1AB=45°-30°=15°;
同理求得,∠P2AG=30°,∠P2AB=45°+30°=75°.
∴∠PAB的度数为15°或75°.
探究二:△AMN的周长存在有最小值.
如答图3所示,连接AD.
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201307/112/88e6bfe5.png" \* MERGEFORMATINET
∵△ABC为等腰直角三角形,点D为斜边BC的中点,
∴AD=CD,∠C=∠MAD=45°.
∵∠EDF=90°,∠ADC=90°,
∴∠MDA=∠NDC.
∵在△AMD与△CND中,
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
∴△AMD≌△CND(ASA).
∴AM=CN.
设AM=x,则CN=x,AN=AC-CN= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 BC-CN= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 -x.[
在Rt△AMN中,由勾股定理得:
MN= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 = HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
△AMN的周长为:AM+AN+MN= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 + HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
当x= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 时,有最小值,最小值为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 = HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
∴△AMN周长的最小值为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .[来源:21世纪教育网]
点评:本题是几何综合题,考查了解直角三 ( http: / / www.21cnjy.com )角形、勾股定理、全等三角形、二次函数最值等知识点.难点在于第(3)问,由发现并证明△AMD≌△CND取得解题的突破点,再利用勾股定理和二次函数的性质求出最小值.
探究型问题]
一、选择题
1.(2013 永州)如图,下列条件中能判定直线l1∥l2的是( )
A.∠1=∠2 B.∠1=∠5 C.∠1+∠3=180° D.∠3=∠5
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201307/21/f7dcb4b9.png" \* MERGEFORMATINET
1.C
2.(2013 安顺)如图,已知AE=CF,∠AFD=∠CEB,那么添加下列一个条件后,仍无法判定△ADF≌△CBE的是( )
A.∠A=∠C B.AD=CB C.BE=DF D.AD∥BC
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201306/98/d86a75c5.png" \* MERGEFORMATINET
2.B
3.(2013 湘潭)如图,在△ABC中 ( http: / / www.21cnjy.com ),AB=AC,点D、E在BC上,连接AD、AE,如果只添加一个条件使∠DAB=∠EAC,则添加的条件不能为( )
A.BD=CE B.AD=AE C.DA=DE D.BE=CD
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201307/10/810af566.png" \* MERGEFORMATINET
3.C
[中~国%&*教育出︿版网]
二、填空题
4.(2013 娄底)如图,AB=AC,要使△ABE≌△ACD,应添加的条件是 ∠B=∠C或AE=AD
(添加一个条件即可).
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201307/24/577f9285.png" \* MERGEFORMATINET
4.∠B=∠C或AE=AD
5.(2013 白银)如图,已知BC=EC,∠BCE=∠ACD,要使△ABC≌△DEC,则应添加的一个条件为 AC=CD
.(答案不唯一,只需填一个)[来~源:中国教育出版%&网︿#]
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201306/106/54af345d.png" \* MERGEFORMATINET
5.AC=CD
6.(2013 上海)如图,在△ABC和△DEF中,点B、F、C、E在同一直线上,BF=CE,AC∥DF,请添加一个条件,使△ABC≌△DEF,这个添加的条件可以是 AC=DF
.(只需写一个,不添加辅助线)
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201306/71/6c44a2d9.png" \* MERGEFORMATINET
6.AC=DF
7.(2013 黑龙江)如图所示,平行四边形ABCD的对角线AC、BD相交于点O,试添加一个条件: AD=DC
,使得平行四边形ABCD为菱形.
7.AD=DC
8.(2013 西城区一模)在平面直角坐标系xOy中,有一只电子青蛙在点A(1,0)处.
第一次,它从点A先向右跳跃1个单位,再向上跳跃1个单位到达点A1;
第二次,它从点A1先向左跳跃2个单位,再向下跳跃2个单位到达点A2;
第三次,它从点A2先向右跳跃3个单位,再向上跳跃3个单位到达点A3;
第四次,它从点A3先向左跳跃4个单位,再向下跳跃4个单位到达点A4;
依此规律进行,点A6的坐标为 (-2-3)
;若点An的坐标为(2013,2012),则n= 4023
.[中
8.(-2-3),4023
9.(2013 湛江)如图,所有正三角形的一边平行于x轴,一顶点在y轴上.从内到外,它们的边长依次为2,4,6,8,…,顶点依次用A1、A2、A3、A4…表示,其中A1A2与x轴、底边A1A2与A4A5、A4A5与A7A8、…均相距一个单位,则顶点A3的坐标是 -1)
,A92的坐标是 (31,-31)
.
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201306/68/370e22ea.png" \* MERGEFORMATINET
9.(0, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ),(31,-31)
10.(2013 绍兴)如图钢架中,焊上等 ( http: / / www.21cnjy.com )长的13根钢条来加固钢架,若AP1=P1P2=P2P3=…=P13P14=P14A,则∠A的度数是 12°
.
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201307/44/114660b3.png" \* MERGEFORMATINET
10.12°
三、解答题
11.(2013 茂名)如图,在 ABCD中,点E是AB边的中点,DE与CB的延长线交于点F.[来
(1)求证:△ADE≌△BFE;
(2)若DF平分∠ADC,连接CE.试判断CE和DF的位置关系,并说明理由.
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201307/65/f0800fb5.png" \* MERGEFORMATINET
11.解:(1)证明:∵四边形ABCD是平行四边形,
∴AD∥BC.
又∵点F在CB的延长线上,
∴AD∥CF,
∴∠1=∠2.
∵点E是AB边的中点,
∴AE=BE.
∵在△ADE与△BFE中,
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,21世纪教育网
∴△ADE≌△BFE(AAS);
(2)解:CE⊥DF.理由如下:
如图,连接CE.
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201307/76/d0fc22bc.png" \* MERGEFORMATINET
由(1)知,△ADE≌△BFE,
∴DE=FE,即点E是DF的中点,∠1=∠2.
∵DF平分∠ADC,
∴∠1=∠3,
∴∠3=∠2,
∴CD=CF,
∴CE⊥DF.
12.(2013 白银)如图,在△ABC ( http: / / www.21cnjy.com )中,D是BC边上的一点,E是AD的中点,过A点作BC的平行线交CE的延长线于点F,且AF=BD,连接BF.
(1)BD与CD有什么数量关系,并说明理由;
(2)当△ABC满足什么条件时,四边形AFBD是矩形?并说明理由.
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201208/30/b8538211.png" \* MERGEFORMATINET
12.解:(1)BD=CD.
理由如下:∵AF∥BC,
∴∠AFE=∠DCE,
∵E是AD的中点,
∴AE=DE,
在△AEF和△DEC中, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
∴△AEF≌△DEC(AAS),
∴AF=CD,
∵AF=BD,
∴BD=CD;
(2)当△ABC满足:AB=AC时,四边形AFBD是矩形.
理由如下:∵AF∥BD,AF=BD,
∴四边形AFBD是平行四边形,
∵AB=AC,BD=CD,
∴∠ADB=90°,
∴ AFBD是矩形.
13.(2013 无锡) ( http: / / www.21cnjy.com )如图,四边形ABCD中,对角线AC与BD相交于点O,在①AB∥CD;②AO=CO;③AD=BC中任意选取两个作为条件,“四边形ABCD是平行四边形”为结论构造命题.
(1)以①②作为条件构成的命题是真命题吗?若是,请证明;若不是,请举出反例;
(2)写出按题意构成的所有命题中的假命题,并举出反例加以说明.(命题请写成“如果…,那么….”的形式)
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201307/14/ad9fdcce.png" \* MERGEFORMATINET
13.(1)以①②作为条件构成的命题是真命题,
证明:∵AB∥CD,
∴△AOB∽△COD,
∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
∵AO=OC,
∴OB=OD,
∴四边形ABCD是平行四边形.
(2)根据①③作为条件构成的命题是假命题,即如果有一组对边平行,而另一组对边相等的四边形时平行四边形,如等腰梯形符合,但不是平行四边形;
根据②③作为条件构成的命题是假命题,即如果一个四边形ABCD的对角线交于O,且OA=OC,AD=BC,那么这个四边形时平行四边形,如图,
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201307/21/dbeb55f2.png" \* MERGEFORMATINET
根据已知不能推出OB=OD或AD∥BC或AB=DC,即四边形不是平行四边形.[来源:z~@z︿step.#*com]
14.(2013 宁波)已知抛物线y=ax2+bx+c与x轴交于点A(1,0),B(3,0),且过点C(0,-3).
(1)求抛物线的解析式和顶点坐标;
(2)请你写出一种平移的方法,使平移后抛物线的顶点落在直线y=-x上,并写出平移后抛物线的解析式.[中%国教*~育︿出版网@]
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "../AppData/Local/Temp/Application%20Data/360se6/User%20Data/Temp/f403c292.png" \* MERGEFORMAT
14.解:(1)∵抛物线与x轴交于点A(1,0),B(3,0),
可设抛物线解析式为y=a(x-1)(x-3),
把C(0,-3)代入得:3a=-3,
解得:a=-1,
故抛物线解析式为y=-(x-1)(x-3),
即y=-x2+4x-3,
∵y=-x2+4x-3=-(x-2)2+1,
∴顶点坐标(2,1);
(2)先向左平移2个单位,再向下平移1个单位,得到的抛物线的解析式为y=-x2,平移后抛物线的顶点为(0,0)落在直线y=-x上.
15.(2013 凉山州)先阅读以下材料,然后解答问题:
材料:将二次函数y=-x2+2x+3的图象向左平移1个单位,再向下平移2个单位,求平移后的抛物线的解析式(平移后抛物线的形状不变).
解:在抛物线y=-x2+2x+3图象上 ( http: / / www.21cnjy.com )任取两点A(0,3)、B(1,4),由题意知:点A向左平移1个单位得到A′(-1,3),再向下平移2个单位得到A″(-1,1);点B向左平移1个单位得到B′(0,4),再向下平移2个单位得到B″(0,2).
设平移后的抛物线的解析式为y=-x2+bx+c.则点A″(-1,1),B″(0,2)在抛物线上.可得:
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,解得: HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .所以平移后的抛物线的解析式为:y=-x2+2.
根据以上信息解答下列问题:
将直线y=2x-3向右平移3个单位,再向上平移1个单位,求平移后的直线的解析式.
15.解:在直线y=2x-3上任取一点A(0,-3),由题意知A向右平移3个单位,再向上平移1个单位得到A′(3,-2),
设平移后的解析式为y=2x+b,
则A′(3,-2)在y=2x+b的解析式上,
-2=2×3+b,
解得:b=-8,
所以平移后的直线的解析式为y=2x-8.
16.(2013 湖州)一节数学课后,老师布置了一道课后练习题:
如图,已知在Rt△ABC中,AB= ( http: / / www.21cnjy.com )BC,∠ABC=90°,BO⊥AC,于点O,点PD分别在AO和BC上,PB=PD,DE⊥AC于点E,求证:△BPO≌△PDE.
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201306/77/7f4b526d.png" \* MERGEFORMATINET
(1)理清思路,完成解答(2)本题证明的思路可用下列框图表示:
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201306/80/051b5901.png" \* MERGEFORMATINET
根据上述思路,请你完整地书写本题的证明过程.
(2)特殊位置,证明结论
若PB平分∠ABO,其余条件不变.求证:AP=CD.
(3)知识迁移,探索新知
若点P是一个动点,点P运动到OC的 ( http: / / www.21cnjy.com )中点P′时,满足题中条件的点D也随之在直线BC上运动到点D′,请直接写出CD′与AP′的数量关系.(不必写解答过程)
16.(1)证明:∵PB=PD,
∴∠2=∠PBD,
∵AB=BC,∠ABC=90°,
∴∠C=45°,
∵BO⊥AC,
∴∠1=45°,
∴∠1=∠C=45°,
∵∠3=∠PBO-∠1,∠4=∠2-∠C,
∴∠3=∠4,
∵BO⊥AC,DE⊥AC,
∴∠BOP=∠PED=90°,
在△BPO和△PDE中
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
∴△BPO≌△PDE(AAS);
(2)证明:由(1)可得:∠3=∠4,
∵BP平分∠ABO,
∴∠ABP=∠3,
∴∠ABP=∠4,]
在△ABP和△CPD中
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 。
∴△ABP≌△CPD(AAS),
∴AP=CD.
(3)解:CD′与AP′的数量关系是CD′= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 AP′.
理由是:如图,
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201306/80/8ee3e1b3.png" \* MERGEFORMATINET
设OP=PC=x,则AO=OC=2x=BO,
则AP=2x+x=3x,
由(2)知BO=PE,
PE=2x,CE=2x-x=x,
∵∠E=90°,∠ECD=∠ACB=45°,
∴DE=x,由勾股定理得:CD= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 x,
即AP=3x,CD= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 x,
∴CD′与AP′的数量关系是CD′= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 AP′
17.(2013 淄博)分别以 ABCD(∠CDA≠90°)的三边AB,CD,DA为斜边作等腰直角三角形,△ABE,△CDG,△ADF.
(1)如图1,当三个等腰直角三角形都在该平行四边形外部时,连接GF,EF.请判断GF与EF的关系(只写结论,不需证明);
(2)如图2,当三个等腰直角三角形都在该平行四边形内部时,连接GF,EF,(1)中结论还成立吗?若成立,给出证明;若不成立,说明理由.
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201307/46/e0cd404a.png" \* MERGEFORMATINET
17.解:(1)∵四边形ABCD是平行四边形,
∴AB=CD,∠DAB+∠ADC=180°,
∵△ABE,△CDG,△ADF都是等腰直角三角形,
∴DG=CG=AE=BE,DF=AF,∠CDG=∠ADF=∠BAE=45°,
∴∠GDF=∠GDC+∠CDA+∠ADF=90°+∠CDA,
∠EAF=360°-∠BAE-∠DAF-∠BAD=270°-(180°-∠CDA)=90°+∠CDA,[来源:21世纪教育网]
∴∠FDG=∠EAF,
∵在△EAF和△GDF中,
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
∴△EAF≌△GDF(SAS),
∴EF=FG,∠EFA=∠DFG,即∠GFD+∠GFA=∠EFA+∠GFA,
∴∠GFE=90°,
∴GF⊥EF;
(2)GF⊥EF,GF=EF成立;
理由:∵四边形ABCD是平行四边形,
∴AB=CD,∠DAB+∠ADC=180°,
∵△ABE,△CDG,△ADF都是等腰直角三角形,
∴DG=CG=AE=BE,DF=AF,∠CDG=∠ADF=∠BAE=45°,
∴∠BAE+∠FDA+∠EAF+∠ADF+∠FDC=180°,
∴∠EAF+∠CDF=45°,
∵∠CDF+∠GDF=45°,
∴∠FDG=∠EAF,
∵在△EAF和△GDF中,
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
∴△EAF≌△GDF(SAS),
∴EF=FG,∠EFA=∠DFG,即∠GFD+∠GFA=∠EFA+∠GFA,
∴∠GFE=90°,
∴GF⊥EF.
18.(2013 张家界)如图,△ABC中 ( http: / / www.21cnjy.com ),点O是边AC上一个动点,过O作直线MN∥BC.设MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F.
(1)求证:OE=OF;
(2)若CE=12,CF=5,求OC的长;
(3)当点O在边AC上运动到什么位置时,四边形AECF是矩形?并说明理由.
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201306/106/555ab352.png" \* MERGEFORMATINET
18.(1)证明:如图,[
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201306/108/a031e6eb.png" \* MERGEFORMATINET
∵MN交∠ACB的平分线于点E,交∠ACB的外角平分线于点F,
∴∠2=∠5,4=∠6,
∵MN∥BC,
∴∠1=∠5,3=∠6,
∴∠1=∠2,∠3=∠4,
∴EO=CO,FO=CO,
∴OE=OF;
(2)∵∠2=∠5,∠4=∠6,
∴∠2+∠4=∠5+∠6=90°,
∵CE=12,CF=5,
∴EF= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 =13,
∴OC= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 EF=6.5;
(3)答:当点O在边AC上运动到AC中点时,四边形AECF是矩形.
证明:当O为AC的中点时,AO=CO,
∵EO=FO,
∴四边形AECF是平行四边形,
∵∠ECF=90°,
∴平行四边形AECF是矩形.
19.(2013 衡阳)如图,P为正方形ABCD的边AD上的一个动点,AE⊥BP,CF⊥BP,垂足分别为点E、F,已知AD=4.
(1)试说明AE2+CF2的值是一个常数;
(2)过点P作PM∥FC交CD于点M,点P在何位置时线段DM最长,并求出此时DM的值.
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201306/87/a011bf86.png" \* MERGEFORMATINET
19.解:(1)由已知∠AEB=∠BFC=90°,AB=BC,
又∵∠ABE+∠FBC=∠BCF+∠FBC,
∴∠ABE=∠BCF,
∵在△ABE和△BCF中,
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
∴△ABE≌△BCF(AAS),
∴AE=BF,
∴AE2+CF2=BF2+CF2=BC2=16为常数;
(2)设AP=x,则PD=4-x,
由已知∠DPM=∠PAE=∠ABP,
∴△PDM∽△BAP,
∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
即 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
∴DM= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
当x=2时,DM有最大值为1.
20.(2013 宁夏)在 ( http: / / www.21cnjy.com ) ABCD中,P是AB边上的任意一点,过P点作PE⊥AB,交AD于E,连结CE,CP.已知∠A=60°;[来%源︿#:&中教网@]
(1)若BC=8,AB=6,当AP的长为多少时,△CPE的面积最大,并求出面积的最大值.
(2)试探究当△CPE≌△CPB时, ABCD的两边AB与BC应满足什么关系?
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201307/14/f39d600c.png" \* MERGEFORMATINET [
20.解:(1)如图,延长PE交CD的延长线于F,
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201307/23/7ed9ec7e.png" \* MERGEFORMATINET
设AP=x,△CPE的面积为y,
∵四边形ABCD为平行四边形,
∴AB=DC=6,AD=BC=8,
∵Rt△APE,∠A=60°,
∴∠PEA=30°,
∴AE=2x,PE= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 x,
在Rt△DEF中,∠DEF=∠PEA=30°,DE=AD-AE=8-2x,
∴DF= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 DE=4-x,
∵AB∥CD,PF⊥AB,
∴PF⊥CD,
∴S△CPE= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 PE CF,
即y= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 × HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 x×(10-x)=- HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 x2+5 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 x,
配方得:y=- HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 (x-5)2+ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
当x=5时,y有最大值 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
即AP的长为5时,△CPE的面积最大,最大面积是 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ;
(2)当△CPE≌△CPB时,有BC=CE,∠B=∠PEC=120°,
∴∠CED=180°-∠AEP-∠PEC=30°,
∵∠ADC=120°,
∴∠ECD=∠CED=180°-120°-30°=30°,
∴DE=CD,即△EDC是等腰三角形,
过D作DM⊥CE于M,则CM= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 CE,
在Rt△CMD中,∠ECD=30°,
∴cos30°= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
∴CM= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 CD,
∴CE= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 CD,
∵BC=CE,AB=CD,
∴BC= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 AB,
则当△CPE≌△CPB时,BC与AB满足的关系为BC= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 AB.
21.(2013 南平)在矩形ABCD中,点E在BC边上,过E作EF⊥AC于F,G为线段AE的中点,连接BF、FG、GB.设 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 =k.
(1)证明:△BGF是等腰三角形;
(2)当k为何值时,△BGF是等边三角形?
(3)我们知道:在一个三角形中,等边所对的角相等;反过来,等角所对的边也相等.事实上,在一个三角形中,较大的边所对的角也较大;反之也成立.
利用上述结论,探究:当△BGF分别为锐角、直角、钝角三角形时,k的取值范围.
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201307/66/e6843b8b.png" \* MERGEFORMATINET
21.解:(1)证明:∵EF⊥AC于点F,
∴∠AFE=90°[
∵在Rt△AEF中,G为斜边AE的中点,
∴GF= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 AE,
在Rt△ABE中,同理可得BG= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 AE,
∴GF=GB,
∴△BGF为等腰三角形;
(2)当△BGF为等边三角形时,∠BGF=60°
∵GF=GB=AG,
∴∠BGE=2∠BAE,∠FGE=2∠CAE
∴∠BGF=2∠BAC,
∴∠BAC=30°,
∴∠ACB=60°,
∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 =tan∠ACB= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
∴当k= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 时,△BGF为等边三角形;
(3)由(1)得△BGF为等腰三角形,由(2)得∠BAC= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ∠BGF,
∴当△BGF为锐角三角形时,∠BGF<90°,
∴∠BAC<45°,
∴AB>BC,
∴k= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 >1;
当△BGF为直角三角形时,∠BGF=90°,
∴∠BAC=45°
∴AB=BC,
∴k= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 =1;
当△BGF为钝角三角形时,∠BGF>90°,
∴∠BAC>45°[
∴AB<BC,
∴k= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 <1;
∴0<k<1.
22.(2013 德阳) ( http: / / www.21cnjy.com )如图,已知AB是⊙O直径,BC是⊙O的弦,弦ED⊥AB于点F,交BC于点G,过点C作⊙O的切线与ED的延长线交于点P.
(1)求证:PC=PG;21世纪教育网
(2)点C在劣弧AD上运动时,其他条件不变,若点G是BC的中点,试探究CG、BF、BO三者之间的数量关系,并写出证明过程;
(3)在满足(2)的条件下,已知⊙O的半径为5,若点O到BC的距离为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 时,求弦ED的长.
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201307/67/ee1cbaa1.png" \* MERGEFORMATINET
22.(1)证明:连结OC,如图,
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201307/94/e5ce4806.png" \* MERGEFORMATINET
∵PC为⊙O的切线,
∴OC⊥PC,
∴∠OCG+∠PCG=90°,
∵ED⊥AB,
∴∠B+∠BGF=90°,
∵OB=OC,
∴∠B=∠OCG,
∴∠PCG=∠BGF,
而∠BGF=∠PGC,
∴∠PGC=∠PCG,
∴PC=PG;
(2)解:CG、BF、BO三者之间的数量关系为CG2=BO BF.理由如下:
连结OG,如图,
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201307/94/e5ce4806.png" \* MERGEFORMATINET
∵点G是BC的中点,
∴OG⊥BC,BG=CG,
∴∠OGB=90°,
∵∠OBG=∠GBF,
∴Rt△BOG∽Rt△BGF,
∴BG:BF=BO: BG,
∴BG2=BO BF,
∴CG2=BO BF;
(3)解:连结OE,如图,
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201307/94/e5ce4806.png" \* MERGEFORMATINET
由(2)得BG⊥BC,
∴OG= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
在Rt△OBG中,OB=5,
∴BG= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 =2 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
由(2)得BG2=BO BF,
∴BF= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 =4,
∴OF=1,
在Rt△OEF中,EF= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 =2 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
∵AB⊥ED,
∴EF=DF,
∴DE=2EF=4 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
23.(2013 泉州)如图1,在平面直角坐标系中,正方形OABC的顶点A(-6,0),过点E(-2,0)作EF∥AB,交BO于F;
(1)求EF的长;
(2)过点F作直线l分别与直线AO、直线BC交于点H、G;
①根据上述语句,在图1上画出图形,并证明 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ;
②过点G作直线GD∥AB,交x轴于点D,以圆O为圆心,OH长为半径在x轴上方作半圆(包括直径两端点),使它与GD有公共点P.如图2所示,当直线l绕点F旋转时,点P也随之运动,证明: HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,并通过操作、观察,直接写出BG长度的取值范围(不必说理);
(3)在(2)中,若点M(2, HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ),探索2PO+PM的最小值.
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201307/106/4a47676d.png" \* MERGEFORMATINET
23.(1)解:解法一:在正方形OABC中,
∠FOE=∠BOA= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ∠COA=45°.
∵EF∥AB,
∴∠FEO=∠BAO=90°,
∴∠EFO=∠FOE=45°,
又E(-2,0),
∴EF=EO=2.
解法二:∵A(-6,0),C(0,6),E(-2,0),
∴OA=AB=6,EO=2,
∵EF∥AB,
∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,即 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
∴EF=6× HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 =2.
(2)①画图,如答图1所示:
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201307/106/23f569c0.png" \* MERGEFORMATINET
证明:∵四边形OABC是正方形,
∴OH∥BC,
∴△OFH∽△BFG,
∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ;
∵EF∥AB,
∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ;
∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
②证明:∵半圆与GD交于点P,
∴OP=OH.
由①得: HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
又EO=2,EA=OA-EO=6-2=4,
∴ HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 = HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
通过操作、观察可得,4≤BG≤12.
(3)解:由(2)可得: HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 = HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
∴2OP+PM=BG+PM.
如答图2所示,过点M作直线MN⊥AB于点N,交GD于点K,则四边形BNKG为矩形,
∴NK=BG.
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201307/106/b151b5b7.png" \* MERGEFORMATINET
∴2OP+PM=BG+PM=NK+PM≥NK+KM,
当点P与点K重合,即当点P在直线MN上时,等号成立.
又∵NK+KM≥MN=8,
当点K在线段MN上时,等号成立.
∴当点P在线段MN上时,2OP+PM的值最小,最小值为8.
24.(2013 梅州)用如图①,②所示的两个直角三角形(部分边长及角的度数在图中已标出),完成以下两个探究问题:
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201307/112/5f1388f5.png" \* MERGEFORMATINET [来源︿:zz&step.co@~m%]
探究一:将以上两个三角形如图③拼接(BC和ED重合),在BC边上有一动点P.
(1)当点P运动到∠CFB的角平分线上时,连接AP,求线段AP的长;
(2)当点P在运动的过程中出现PA=FC时,求∠PAB的度数.21世纪教育网
探究二:如图④,将△DEF的顶点D放在 ( http: / / www.21cnjy.com )△ABC的BC边上的中点处,并以点D为旋转中心旋转△DEF,使△DEF的两直角边与△ABC的两直角边分别交于M、N两点,连接MN.在旋转△DEF的过程中,△AMN的周长是否存在有最小值?若存在,求出它的最小值;若不存在,请说明理由.
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201307/112/154e0a91.png" \* MERGEFORMATINET
24.解:探究一:(1)依题意画出图形,如答图1所示:
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201307/112/20242b76.png" \* MERGEFORMATINET
由题意,得∠CFB=60°,FP为角平分线,则∠CFP=30°,
∴CF=BC sin30°=3× HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 = HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
∴CP=CF tan∠CFP= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 × HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 =1.
过点A作AG⊥BC于点G,则AG= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 BC= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
∴PG=CG-CP= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 -1= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
在Rt△APG中,由勾股定理得:
AP= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
(2)由(1)可知,FC= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
如答图2所示,以点A为圆心,以FC= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 长为半径画弧,与BC交于点P1、P2,则AP1=AP2= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201307/112/2c9d35a5.png" \* MERGEFORMATINET [ww@w#.zzs%t~e&p.com]
过点A过AG⊥BC于点G,则AG= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 BC= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
在Rt△AGP1中,cos∠P1AG= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
∴∠P1AG=30°,[中国教#育%&@出~版网]
∴∠P1AB=45°-30°=15°;
同理求得,∠P2AG=30°,∠P2AB=45°+30°=75°.
∴∠PAB的度数为15°或75°.
探究二:△AMN的周长存在有最小值.
如答图3所示,连接AD.
HYPERLINK "http://www.21cnjy.com" INCLUDEPICTURE "http:///quiz/images/201307/112/88e6bfe5.png" \* MERGEFORMATINET
∵△ABC为等腰直角三角形,点D为斜边BC的中点,
∴AD=CD,∠C=∠MAD=45°.
∵∠EDF=90°,∠ADC=90°,
∴∠MDA=∠NDC.
∵在△AMD与△CND中,
HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
∴△AMD≌△CND(ASA).
∴AM=CN.
设AM=x,则CN=x,AN=AC-CN= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 BC-CN= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 -x.[
在Rt△AMN中,由勾股定理得:
MN= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 = HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
△AMN的周长为:AM+AN+MN= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 + HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 ,
当x= HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 时,有最小值,最小值为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 = HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .
∴△AMN周长的最小值为 HYPERLINK "http://www.21cnjy.com" EMBED Equation.DSMT4 .[来源:21世纪教育网]
点评:本题是几何综合题,考查了解直角三 ( http: / / www.21cnjy.com )角形、勾股定理、全等三角形、二次函数最值等知识点.难点在于第(3)问,由发现并证明△AMD≌△CND取得解题的突破点,再利用勾股定理和二次函数的性质求出最小值.
同课章节目录
